基于安装过程的O形圈安装结构优化分析

蔡智媛 王冰清 彭旭东，2 孟祥铠，2

1.浙江工业大学机械工程学院，杭州，3100322.浙江工业大学过程装备及其再制造教育部工程研究中心,杭州，310032

0 引言

O形圈因结构简单、密封性能良好而在液压设备、工程机械、航空航天等领域起关键密封作用，其质量直接影响到机械设备的工作性能和安全。国内外学者应用数值分析[1-4]和实验分析[5-7]等方法对O形圈的密封机理及性能进行了大量研究。对橡胶密封件在安装和使用中的变形及密封界面上各应力进行精确研究，在实际应用中存在较大的困难。随着数值计算方法、计算机性能等的发展，利用非线性有限元分析软件对密封件在安装和使用中的高度非线性接触问题进行研究成为有效手段，并产生了大量研究成果[8-10]。胡殿印等[8]利用有限元方法分析了针对库存和工作两种状态下O形密封圈的应力及应变，并分析了沟槽结构尺寸、O形圈尺寸、工作温度、操作参数等对密封性能的影响；李殿新等[9]基于有限元分析软件，分析了不同介质压力下橡胶O形圈前后支撑的变形和受力情况；ZHANG 等[10]利用ANSYS Workbench软件研究了密封流体压力及工作速度下O形圈的应力状态，给出了往复O形圈的失效准则。但是，对于O形圈安装预压缩过程的数值模拟，以上研究通常都通过对轴或活塞施加径向位移模拟O形圈的过盈装配过程，这显然与实际安装方式不同，且忽略了O形圈在实际安装预压缩过程中发生的行为变化。

在实际使用过程中，O形圈会经历一个装配过程，首先将O形圈向内折弯变形后装入沟槽中，再将往复轴沿轴向方向推入，迫使O形圈拉伸变形内径变大，由于橡胶O形圈的弹性变形恢复趋势而产生挤压，从而完成O形圈的安装及预压缩过程。而在实际安装过程中，O形圈极容易由于不当操作造成划伤、扭转、过量拉伸等损坏而降低使用寿命甚至无法使用，因此GB/T 3452.3—2005《液压气动用O形橡胶密封圈 沟槽尺寸》规定，在需要与O形橡胶圈接触的轴端、O形圈安装过程中会经过的孔端都需要加工15°～20°的引入角，以避免对O形圈造成损坏。而在现有的针对O形圈的有限元模拟分析中，普遍采用通过轴或活塞的径向位移实现O形圈安装预压缩过程的方法，进而简化了O形圈的安装过程，这显然会与O形圈实际安装预压缩过程中的行为变化存在差异。这一差异已经引起了部分学者的关注，从而针对O形圈实际安装过程进行了有限元分析，但只是建立了轴向推进的有限元模型，与常用的径向压缩模型进行了对比分析，并没有对实际安装预压缩过程的O形圈行为变化及安装过程中各因素对O形圈密封性能的影响进行系统深入的研究[11-12]。

本文以O形圈为研究对象，在ANSYS软件中建立二维轴对称几何模型，采用更符合实际的轴向推进预压缩有限元模型对密封圈的安装过程进行模拟，研究其安装行为，预判O形圈安装过程的易失效部位；根据现行国标给出的范围分析压缩率、引入角等参数对O形圈密封性能的影响，给出O形圈的最佳安装参数，以期为修正和完善国标提供参考，对橡胶O形圈的安装结构设计提供理论参考。

1 计算模型及方法

1.1 几何模型

O形密封圈具体的安装过程如图1所示。采用轴向推进模拟安装预压缩过程的有限元分析模型(下文简称安装模型)的几何示意图见图2。由图2可知，整个密封系统由O形圈、缸体和轴三部分组成。对于O形密封圈，其几何尺寸根据国标GB/T3452.3—2005选取，尺寸为φ42.5 mm×5.3 mm。沟槽形式为矩形槽，其尺寸设计严格按照GB/T3452.3—2005选取。图2中标注了与轴端安装引入角有关的参数，分别为：引入角角度θ，引入角内端圆角半径R1，引入角外端圆角半径R2，引入长度Z。

图2 有限元仿真几何模型Fig.2 Geometric model for finite element analysis

1.2 计算模型的建立

O形圈材料为丁腈橡胶(NBR)，弹性模量E=43 MPa，泊松比ν=0.499，其变形具有很强的材料和几何非线性。在非线性有限元问题的求解过程中，材料的应力-应变关系一般用应变能密度函数来描述。针对橡胶材料的应力-应变关系，国内外学者通过大量的实验研究，总结规律，针对不同的使用特点提出了描述该类材料特性的不同本构模型，例如Neo-Hookean、Klosne-Segal、Mooney-Rivlin(M-R)模型等[13]。M-R模型能够在中小应变下保持较高精度的描述橡胶材料的真实特性，满足研究分析的需求且被大量的实验验证[14]。本文为使有限元模拟仿真更接近实际情况，结合使用二参数的M-R超弹模型和能很好描述橡胶材料蠕变、松弛等特性的Prony剪切响应黏弹模型作为橡胶O形圈的材料模型。其中，M-R超弹模型的参数如下：C10=0.2，C01=6.0，d=0.000 279[15]；Prony剪切响应黏弹模型的加权系数αi和松弛时间τi分别取：α1=0.333 33，τ1=0.4，α2=0.333 33，τ2=0.2[16]。

采用ANSYS建立轴向推进安装的O形圈密封的二维轴对称有限元模型，设定为平面六节点单元 PLANE 183。合理选择分析网格的数量及类型，是保证较高计算效率和可靠计算精度的有效手段[17]。通过网格无关性验证发现，采用重点分析接触区域局部加密、非重点分析区域不加密的网格绘制方法，能保持较好的计算精度和较高的计算效率，当网格数在16 800～ 35 600范围时，计算结果误差始终稳定在5%以内，因此，本文对有限元模型采用自由网格绘制，网格数量为25 463。轴和缸体材料通常为常用金属材料，因为金属材料的弹性模量远大于橡胶材料的弹性模量，所以在有限元模拟分析时对金属部件作刚体处理[18]。密封圈与沟槽及轴的接触是高度的非线性行为，建立橡胶弹性体与轴、沟槽2个接触对，设置密封各部件之间接触对的接触方式均为面-面接触，接触类型为刚-柔接触。O形圈与密封沟槽、轴的摩擦因数均设为0.25[19]。采用加强的拉格朗日接触算法。

分析过程的具体边界条件设置如下：所有过程中缸体均施加位移全约束。为实现实际安装过程的模拟仿真，首先对上述有限元模型的轴施加x轴负方向的位移，位移量为O形圈单边压缩量；然后对轴施加y轴正方向的位移，使轴能达到密封圈初始安装的位置，从而完成对O形圈的安装预压缩过程。

2 计算结果分析

2.1 安装过程中O形圈力学性能

对密封结构引入角各参数值分别为θ=20°、Z=3 mm、R1=2 mm、R2=1 mm和压缩率为12%的情况进行仿真，安装模型计算得出的O形密封圈的等效应力和平面剪切应力随安装进程尺寸d变化的曲线及分布云图见图3。

由图3中变化曲线可知，在安装状态下，采用轴向安装模型分析计算绘制O形圈等效应力和平面剪切应力变化曲线，趋势都是先陡增大到最大值，然后缓慢降低逐渐趋于平稳，故均存在一个明显的安装峰值，两种应力的安装峰值分别为8.43 MPa和4.62 MPa，比轴完全装入后趋于稳定的应力值分别超出162%和207%。而安装应力峰值对应的位置都在O形圈与轴端引入角内端圆角接触处，靠近轴端引入角完成安装的地方，这是由于在轴的轴向运动过程中，橡胶O形圈受轴端引入角与其之间摩擦力及引入角作用于圈上的轴向力的共同作用，挤压带动橡胶圈材料朝着轴向向安装间隙方向运动，随着挤压移动加剧，沟槽侧壁的阻碍作用不断加强，因此，橡胶材料不断向密封间隙堆积出现安装峰值。这一现象表明O形圈该处在实际安装过程中可能很容易发生“畸变”，且安装应力过大时很容易引起O形圈的材料损伤和永久变形[20]。而随着轴的不断移动以及橡胶材料不断地向密封间隙堆积，沟槽侧壁传递给O形圈的反作用力不断增大，而引入角作用的轴向力不断减小，当反作用力超过轴与O形圈之间的摩擦力和引入角作用于O形圈的轴向力之和时，橡胶O形圈就停止向密封间隙运动且随着时间推移开始回弹，因此，O形圈内部的应力开始减小；当轴端引入角完全装入时，引入角提供的轴向力突然消失，挤入密封间隙的橡胶材料迅速回弹，从而使O形圈内部应力先迅速减小，然后减小速度放缓，逐渐趋近理想预压缩状态的应力值。

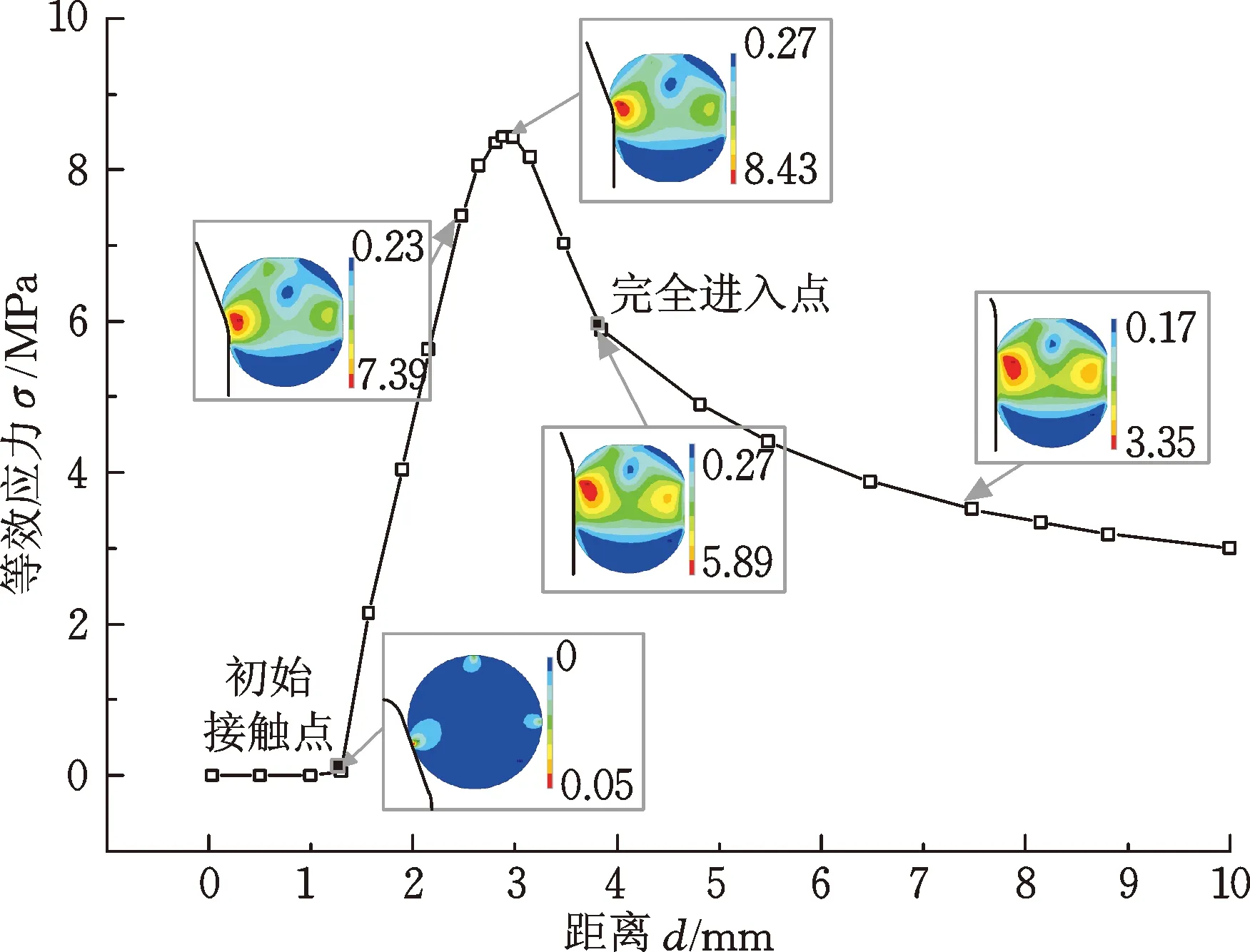
(a) 等效应力曲线及云图

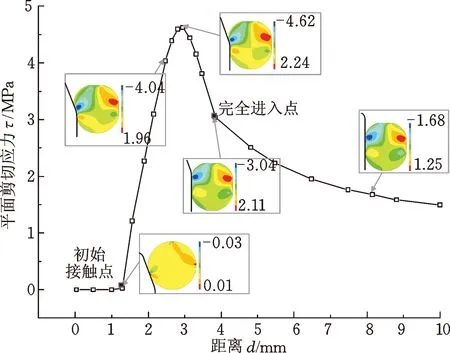
(b) 平面剪切应力曲线及云图图3 安装过程各应力变化曲线及云图Fig.3 Stress distributions & Curve of the installation process

2.2 影响安装过程应力峰值因素分析

压缩率及摩擦因数是安装预压缩过程的两个非常重要的操作参数。在工程应用中，通常通过设计加工不同的沟槽深度，改变与轴的密封间隙来实现不同的密封圈安装压缩率，而在轴表面涂抹润滑介质等来改变摩擦因数，因此在模拟分析中可以改变这两种操作参数，研究其对O形圈力学性能的影响。在GB/T3452.3—2005中，为避免橡胶O形圈在安装过程被损坏，规定在安装经过O形圈的轴的端部需要加工引入角；引入角的几何结构参数包括引入角角度θ，引入角内端圆角半径R1，引入角外端圆角半径R2和引入长度Z，而现行国标只规定了引入角角度θ和引入长度Z两个量的数值范围(15°<θ<20°，Z>2.7 mm)，不仅对不同的使用工况没有具体的标准，且对两个圆角半径的取值没有给出参考范围。

上述操作及结构参数对各安装应力的影响规律变化曲线分别如图4～图8所示。当θ=20°、Z=3 mm、R1=2 mm和R2=1 mm时，压缩率ε和摩擦因数μ的变化引起各应力的变化规律曲线如图4、图5所示。可以看出，随着压缩率和摩擦因数的改变，各应力安装峰值会受到直接影响，且随着压缩率和摩擦因数的增大，安装峰值会相应变大，而压缩率和摩擦因数的变化会直接影响O形圈与轴之间的接触摩擦力。因此，在实际装配使用中，在满足密封条件的基础上，采用较小的压缩率和进行良好的润滑处理可以有效避免安装损坏和提高密封件工作质量，而在需要较大压缩率达到密封要求时，通过涂抹润滑介质、减缓安装速度等，可有效避免橡胶O形圈安装损坏。

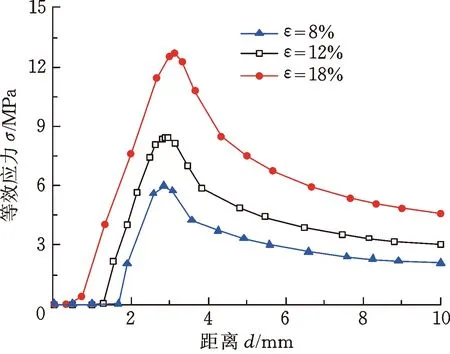
(a) 等效应力

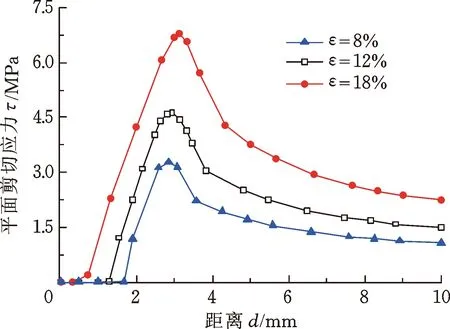
(b) 平面剪切应力图4 不同压缩率下应力变化曲线Fig.4 Stress change with time versus under different compression ratio

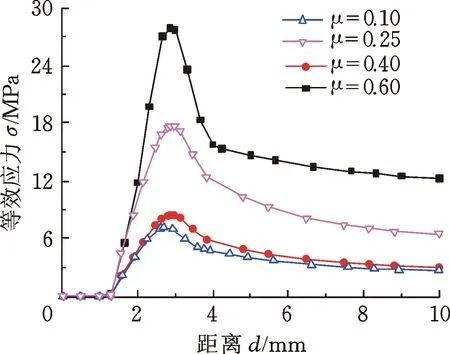
(a) 等效应力

当压缩率为12%、摩擦因数为0.25时，改变引入角内端圆角半径R1、引入角角度θ和引入长度Z，对应各应力峰值的变化曲线如图6～图8所示。引入角外端圆角在此工况下整个安装过程中与O形圈并未发生接触，故不考虑R2值对密封圈应力的影响。由图6可以看出，各应力安装峰值随着引入角内端圆角半径R1的增大而减小，当R1由0.1 mm增至2 mm时，等效应力和平面剪切应力安装峰值分别减小了17.33%和18.38%，而当R1由0.1 mm增至5 mm时，等效应力和平面剪切应力的安装峰值则分别减小了30.73%和32.29%，由此可以看出，当引入角内端圆角半径R1不断增大时，各应力安装峰值的变化幅度反而逐渐减小。根据图7，引入长度Z的变化只对安装峰值出现时对应的安装进程位置有影响而不影响其值，进一步说明造成各应力安装峰值的原因是轴端引入角施加于O形圈的轴向力与接触摩擦力对O形圈的共同挤压作用。由图8可以看出，改变引入角角度θ对各应力安装峰值以及安装峰值出现时对应的安装进程位置都有影响，但影响相对较小。因此，通过综合分析安装引入角结构参数对安装过程的影响发现，改变引入角角度θ和引入角内端圆角半径R1对各应力安装峰值有直接影响，而引入长度Z的变化对其无影响。

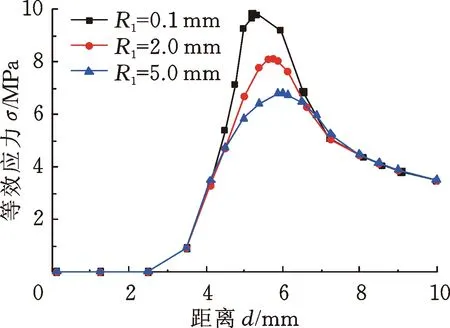
(a) 等效应力

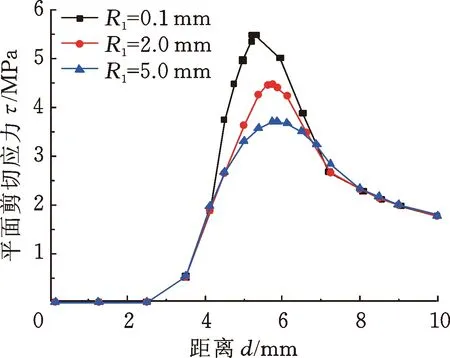
(b) 平面剪切应力图6 不同引入角内端圆角R1下应力变化曲线Fig.6 Stress change with time versus under different R1

(a) 等效应力

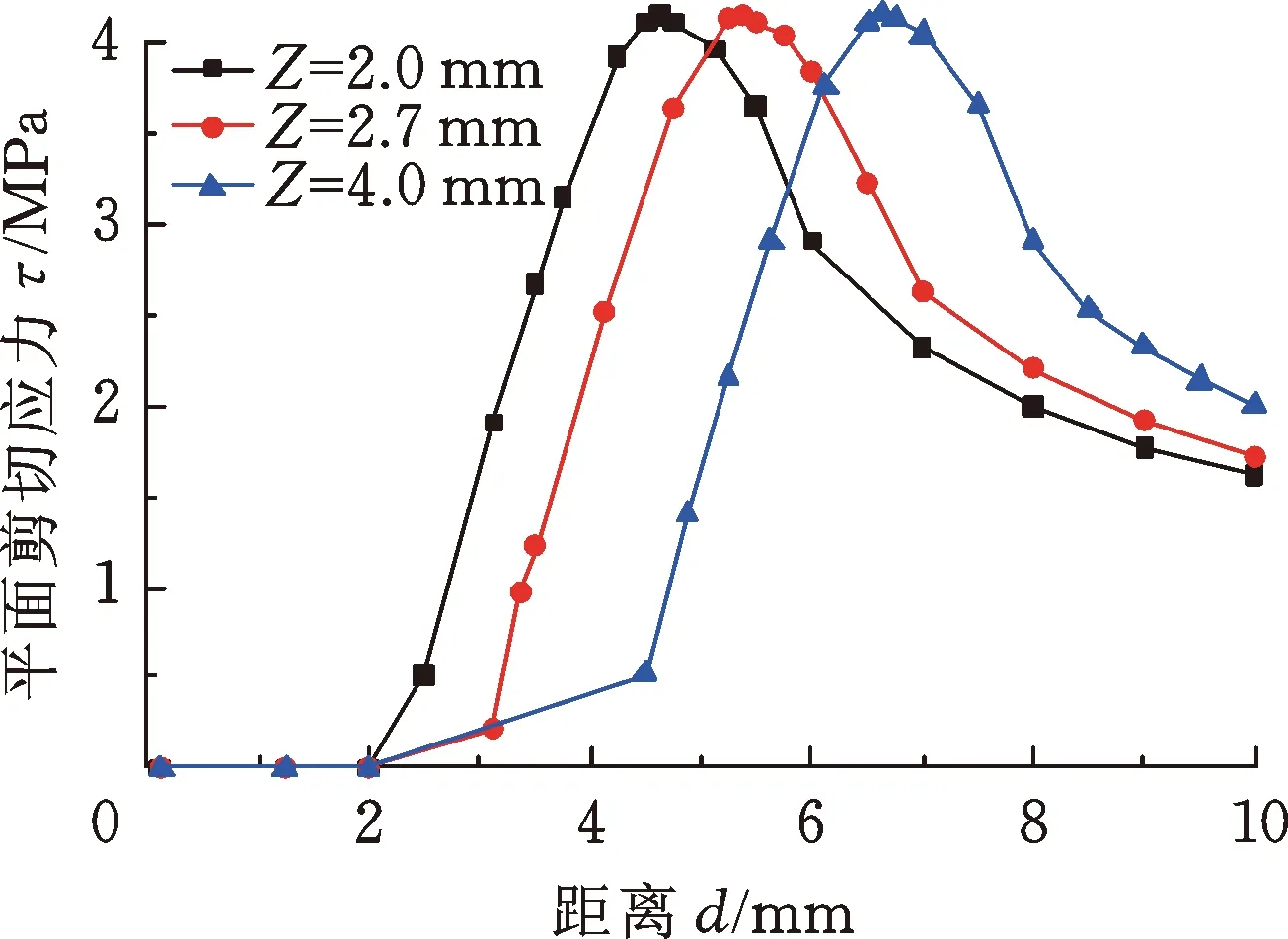
(b) 平面剪切应力图7 不同引入长度Z下应力变化曲线Fig.7 Stress change with time versus under different Length of Lead angle Z

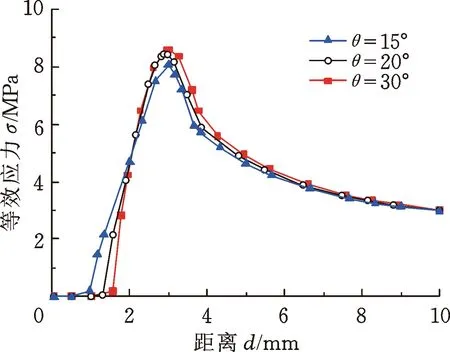
(a) 等效应力

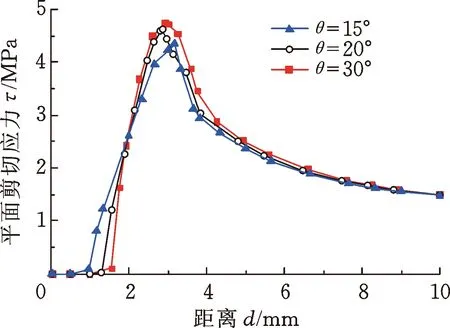
(b) 平面剪切应力图8 不同引入角角度θ下应力变化曲线Fig.8 Stress change with time versus under different lead angle θ

2.3 最佳安装结构参数分析

基于上述分析结果，改变轴端引入角角度θ和引入角内端圆角半径R1对各应力安装峰值以及安装峰值出现时对应的安装进程位置都存在一定影响。应针对上述两种结构参数对安装峰值的影响进行更详细的研究。

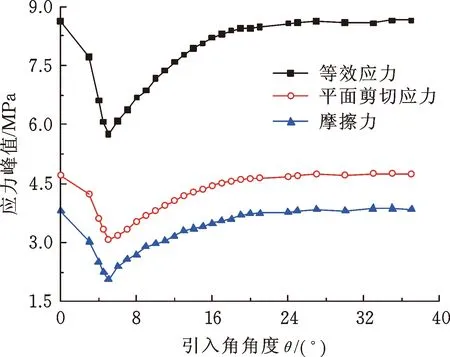
图9 不同引入角角度θ下应力峰值曲线Fig.9 Peak stress curves versus lead angle θ

压缩率为12%，Z=3 mm、R1=2 mm、R2=1 mm和摩擦因数为0.25时，改变引入角角度θ对应的各应力安装峰值的变化曲线如图9所示。由图9可知，随着θ的增大，O形圈的各应力安装峰值先减小，θ为5°左右时安装峰值最小。这一变化趋势原因是，当θ为0°(即不开设引入角)时，在轴安装中轴端引入角外端圆角与O形圈直接接触，没有引入角起到过渡作用；随着θ增至0°～5°之间时，引入角将安装过程中轴作用于O形圈的部分轴向力转换成径向力，减小了O形圈所受的轴向力，且轴端引入角外端圆角辅助O形圈进入引入角，从而减缓了O形圈橡胶材料向密封间隙的运动堆积，由此安装过程中O形圈内部应力的峰值逐渐减小。随着θ的进一步增大，各应力峰值逐渐增大，而在θ=20°时开始趋于平缓，其值不再随θ的变化产生较大改变。这是由于随着θ的进一步增大，轴端引入角外端圆角的过渡作用逐渐消失，转换轴向力的作用小于轴端引入角外端圆角的过渡作用，使O形圈向密封间隙堆积挤压加剧，从而使O形圈内部应力的安装峰值增大，直到轴端引入角外端圆角的过渡作用完全消失，引入角的引入过渡作用逐渐趋于稳定。

操作工况参数和引入角几何参数分别为：ε=12%，Z=3 mm、θ=15°、R2=1 mm和摩擦因数为0.25时，改变R1时对应的各应力安装峰值的变化曲线如图10所示。可以看出，当R1从0.1 mm增至5 mm时，O形圈的各应力安装峰值的整体变化趋势是减小的，但R1在0.1 ～3 mm之间和大于3 mm时减小的速度有所不同，前者区间的各应力安装峰值减小速度较快，后者则随着R1值的进一步增大，安装峰值变化较为缓慢且逐渐趋于某一恒定值。因此，在工程应用中，在轴端引入角加工工艺复杂性与经济成本合理的前提下，基于此种工况下最小引入角角度θmin=5°时，θ应该越接近5°越好，而引入角内端圆角半径R1>3 mm时安装性能较优。

图10 不同R1下应力峰值曲线Fig.10 Peak stress curves versus Inner rounded Corner of lead angle R1

3 结论

(1) 安装时，随着轴的装入，O形圈的各应力变化都有一个明显的安装峰值，比轴安装完成后的最大应力值分别超出162%和207%，且应力安装峰值对应的安装进程位置均出现在与轴端引入角内端圆角接触处，靠近引入角完全进入处，而过大的安装应力容易造成橡胶O形圈的材料损伤和永久变形情况的出现。

(2)对操作参数和安装结构几何参数分别进行研究后发现，压缩率和摩擦因数对安装应力峰值的影响较大，且峰值随两参数的减小而减小，由此在实际安装操作中应选取合适的压缩率，并保证润滑良好；改变引入角角度θ和引入角内端圆角半径R1的值对安装应力峰值有直接影响，且该值随着R1值的增大而减小，而随着θ值的增大呈现先减小后增大、最后趋于稳定的变化情况，而引入长度Z的变化只对安装峰值出现时对应的安装进程位置有影响，不会改变其值大小。

(3) 在O形密封圈的实际装配过程中，考虑加工艺复杂性与经济成本，最小引入角角度θmin=5°时，加工角度θ越接近5°越好，轴端引入角内端圆角半径R1>3 mm时，O形圈安装性能较优。