小样本检测数据驱动的飞机结构件装配关键偏差源诊断
2019-12-02朱永国霍正书周结华
朱永国 邓 斌 霍正书 周结华
1.南昌航空大学航空制造工程学院,南昌,3300632.南昌航空大学信息工程学院,南昌,330063
0 引言
飞机是一种零件数量众多、装配协调关系复杂、装配准确度要求高的典型复杂结构产品,零件制造误差、工装定位误差、薄壁件变形回弹、铆接干涉等众多偏差源累计耦合导致飞机装配经常出现超差现象。对于飞机装配中众多偏差源,如不经筛选就直接用于偏差分析和质量控制,则不能抓住飞机装配质量控制的关键要素[1]。
当前,装配偏差研究主要集中在基于刚性假设的装配偏差传递[2-3]、考虑柔性的装配偏差传递[4-5],以上装配偏差传递模型力图通过建立基于装配尺寸链方程来量化装配偏差源与装配质量之间的关系。飞机装配中存在数量众多的薄壁板件和新型复合材料,薄壁板件的变形与回弹、新型复合材料的内应力使得飞机装配偏差传递与累计呈现出不确定度大、非线性、多层级、强耦合等特点,几乎不能构建基于装配尺寸链方程的装配件偏差计算表达式或依据该计算表达式进行关键偏差源的量化识别。3DCS等三维尺寸公差分析软件可直接用于零件装配偏差分析,具有高准确度[6],但由于其建模复杂、参数设置繁琐,操作人员需熟练掌握装配特征的明确含义和几何公差规范[7],导致仿真周期长、效率低。
近年来,在飞机研制过程中引入激光跟踪仪等数字化测量设备已经成为国内外飞机制造公司的共识[8-10]。充分挖掘这些数字化测量设备测得的数据中所包含的信息,对揭示装配偏差的传播机理具有重要意义。WANG等[11]通过检索零部件历史制造数据,识别了飞机水平安定面结构装配偏差来源。CHENG等[12]将飞机壁板铆接点实测数据与传统的偏差分析手段相结合进行了铆接点最终装配偏差分析。 LIU等[13]通过测量零件搭接配合点实际位置,可提前预测装配间隙或干涉情况。以上方法均没有考虑飞机生产批量小,特别是研制阶段,不适用于飞机装配偏差检测数据样本小的场合。HU等[14]将经验贝叶斯方法引入小样本检测条件下复杂产品制造质量中,该方法的缺点是计算量大,确定合理的先验密度比较困难,需拥有足够数量可信的验前数据,而神经网络又存在收敛速度较慢、计算量大、样本小时网络不稳定等缺陷。
灰色关联分析能够处理信息不完全明确的灰色系统,并对数据样本的容量大小和验前信息均没有要求[15-16],适合小样本的飞机研制数据挖掘。但经典的灰色关联法存在以下2个需改进的地方:①在计算关联度时常采用均一权重,没顾及到装配质量各属性分量权重的差异;②采用绝对关联度量化关联程度,当分析的因素差异较大时,由于变量间的量纲不一致,往往影响分析结果。灰色综合关联度按照两对比数列的相对变化态势的接近程度来计算其因素之间的关联度,通过差异性系数来控制它们之间的权重[17],不仅可描述装配偏差与装配质量的相似程度,而且能反映装配偏差与装配质量之间变化速率的接近程度。
基于以上分析,本文引入测量信息论,将熵权法和灰色综合关联度进行融合,提出小样本数据驱动的飞机结构件装配关键偏差源诊断新方法。
1 小样本检测数据驱动的飞机结构件装配关键偏差源诊断
图1所示为小样本检测数据驱动的飞机结构件装配关键偏差源诊断流程:首先基于装配质量检测数据,利用熵权法构建装配质量多属性评价矩阵,对该矩阵进行解算,得装配质量各分量的权重;然后,利用量化装配偏差与装配质量相似程度和装配偏差与装配质量之间变化速率接近程度的灰色综合关联度描述装配偏差与装配质量之间的关联程度。在装配质量各分量熵权和装配偏差与装配质量灰色综合关联度量化的基础上,建立装配偏差重要程度综合量化评价模型,以识别出影响结构件装配质量的潜在关键偏差源。

图1 小样本检测数据驱动的飞机结构件装配关键偏差源诊断流程Fig.1 The flow of key deviation source diagnosis for aircraft structural component assembly driven by small sample inspection data
1.1 基于熵权法的结构件装配质量属性权重量化表示
结构件装配质量属性的权重依赖于质量属性带有的信息量大小,并且成反比关系。即,熵值越小熵权越大,该质量属性能提供较多有用的信息。为此,引入熵权来量化质量属性的权重,即,利用装配质量检测数据所提供的信息来确定装配质量属性的权重。首先,利用飞机结构件装配过程中获得的装配质量检测数据,构建装配质量多属性评价矩阵;其次,对构建的评价矩阵进行标准化处理;然后,求解结构件装配质量分量比重矩阵;最后,利用熵权法量化结构件装配质量各分量的权重。
1.2 基于灰色综合关联度的结构件装配偏差源与装配质量关联程度量化建模
首先,构建结构件装配偏差与装配质量的分析对比序列,对构建的分析对比序列进行初值化操作,对经过初值化处理的分析对比序列进行始点零化处理;然后,利用灰色绝对关联度和灰色相对关联度的定义分别计算装配偏差与装配质量之间的灰色绝对关联度和灰色相对关联度;最后,利用灰色综合关联度量化结构件装配偏差源与结构件装配质量之间的灰色综合关联度。
1.3 偏差源重要度综合评价
首先,利用熵权法对每个偏差分量进行赋权,通过灰色综合关联度求解每个偏量分差与装配质量之间的灰色综合关联度;然后,利用熵权对灰色综合关联度进行改进,并根据修正结果对装配偏差源进行重要程度排序,值越大表示该偏差源与装配质量之间的关联度越大,即可识别出处于关键地位的偏差源。
基于熵权法和灰色综合关联的飞机结构件装配关键偏差源诊断方法在充分挖掘检测数据所提供信息的基础上既实现了质量属性权重的客观评定,又利用了灰色综合关联在小样本、贫信息分析中的优势。
2 基于熵权法的结构件装配质量属性权重量化表示

(1)

(1)装配质量多属性评价矩阵构建。对xk进行扩展,构建结构件装配质量δ的多属性评价矩阵A:

(2)

(3)装配质量分量比重矩阵确定。计算δk的第i次检测数据占所有测量数据的比重:
(3)
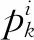
(4)装配质量分量信息熵求解。将P代入式(1),可计算得各质量分量δ1,δ2,…,δk,…,δs的信息熵H1,H2,…,Hk,…,Hs。
(5)质量分量差异性量化表示。根据信息熵的性质将各装配分量的差异性系数定义为Ek:
Ek=1-Hk
(4)
Hk越大,则Ek越小。
(6)各装配质量分量权重求解。利用Ek,可求得各装配质量分量δk的熵权ωk:
(5)
3 基于灰色综合关联度的结构件装配偏差与装配质量关联度量化建模
(6)
式中,x1,x2,…,xs为装配偏差检测数据。
为保证装配偏差检测数据与装配质量评价参数之间的可比性,通过下式对分析对比序列式x0,x1,…,xs进行初值化处理:
(7)
利用式(7)对式(6)进行初值化处理,得
(8)
3.1 装配质量与装配偏差源之间的灰色绝对关联度
利用式(9)对经过初值化处理的分析对比序列(x0)′,(x1)′,…,(xs)′分别进行始点零化处理:
(9)
结合式(8)和式(9),可得(x0)′,(x1)′,…,(xs)′初值化后的分析对比新序列(x0)″,(x1)″,…,(xs)″:
(10)
式中,(xk)″为(xk)′的始点零化象。
利用下式将(xk)″关于偏差检测次序积分:

(11)
计算得
(12)
令
(13)
式中,λ0k为x0和xk之间的绝对关联度。
3.2 装配质量与装配偏差之间的灰色相对关联度
将(xk)′关于偏差检测次序积分:

(14)
计算得
(15)
令

(16)
式中,γ0k为x0和xk之间的灰色相对关联度。
3.3 装配质量与装配偏差之间的灰色综合关联度
综合式(13)求得的绝对关联度λ0k和式(16)求得的相对关联度γ0k,可得序列x0和序列xk之间的灰色综合关联度:
ρ0k=θλ0k+(1-θ)γ0k
(17)
其中,分辨系数θ的取值范围为(0,1),当序列波动较大时,分辨系数取小值;当序列波动较小时,分辨系数取大值。
4 装配偏差源重要程度综合评价
综合式(5)计算得到的ωk和式(17)计算得到的ρ0k量化装配偏差的重要程度,得
(18)
其中,ψ0k为第k个偏差分量的重要度,ψ0k越大,表示该装配偏差与装配质量之间的关联度越大,因此,可依据ψ0k识别出处于关键地位的偏差源。
5 应用案例
以某型号飞机前机身右上壁板结构件装配为研究对象,验证本文提出的飞机装配关键偏差源诊断方法的正确性和可行性。该型号飞机前机身右上壁板由表1所示的变曲率蒙皮、隔框和长桁组成,零件尺寸分别如图2、图3和图4所示,图5所示为该壁板的总体结构。该壁板各零件之间的连接方式为铆接。

表1 某型飞机前机身右上壁板零件Tab.1 Parts of aircraft front fuselage right upper panel mm

图2 某型飞机前机身右上壁板蒙皮Fig.2 Right upper panel skin of aircraft front fuselage

图3 某型飞机前机身右上壁板长桁Fig.3 Right upper panel stringer of aircraft front fuselage

图4 某型飞机前机身右上壁板隔框Fig.4 Right upper panel bulk head of aircraft front fuselage

图5 某型飞机前机身右上壁板结构Fig.5 Right upper panel structure of aircraft front fuselage
5.1 基于3DCS的某型号飞机前机身右上壁板装配偏差仿真

图6 基于3DCS的右上壁板柔性装配仿真Fig.6 Flexible assembly simulation of right upper panel based on 3DCS
图6所示为利用3DCS软件进行右上壁板装配关键偏差源诊断的流程。首先,将蒙皮、隔框和长桁的网格文件和缩减刚度矩阵分别加载到仿真模型中,作为计算变形的依据。然后,将蒙皮、隔框、长桁等模拟件定位夹紧到夹具上,并进行铆接仿真。其次,松开各个零件的夹持和定位,此时壁板装配件将会发生回弹。最后,根据《装配容差控制通用要求》对整机装配工艺设定偏差,并利用蒙特卡洛分析方法进行5架次装配偏差仿真。网格文件单元类型均设置为C3D10;蒙皮、隔框和长桁的材料属性均相同,其中弹性模量为2×1011Pa,泊松比为0.266,密度为7 860 kg/m3,延展率为1.17×10-5。
5.1.1右上壁板装配质量关键控制点创建
工程实际中,采用蒙皮外形关键控制点形变量(即关键控制点形变后的位置与初始位置之间的距离)来表征该壁板的装配质量。依据右上壁板装配质量关键控制点的设计要求,关键控制点分布在蒙皮外侧径向边缘1/3、2/3处,共有4个关键控制点,图7所示为通过关键控制点来表征壁板的装配质量。

图7 某型号飞机前机身右上壁板质量关键控制点Fig.7 Key quality control points of aircraft front fuselage right upper panel
5.1.2右上壁板定位点制造偏差
根据《装配容差控制通用要求》整机装配中的公差规范,设定表2所示的隔框4个定位点制造偏差,表2中F1-P1表示第一个隔框第一个定位点的位置度偏差,其他定义以此类推。
5.1.3蒙特卡洛装配偏差仿真
利用3DCS软件进行5架次右上壁板柔性装配仿真,表3所示为5次仿真各关键控制点的形变量偏差。

表2 隔框制造偏差Tab.2 Manufacturing deviations of bulkheads mm

表3 关键控制点位置度偏差Tab.3 Deviations of key control points mm
通过3DCS软件的Geofactor对每个关键控制点进行偏差赋值;通过装配将各偏差源进行累计,获得装配件的累计偏差;再通过分析可获得各偏差源对装配累计偏差的贡献率,从而得到各关键控制点对装配质量的影响。在利用Geofactor方法得到每个关键控制点对右上壁板整体装配质量的影响的基础上,将所有关键控制点的影响值进行平方和相加,单点影响值的平方值除以平方和就能够得到综合贡献度。平等对待每架次分析结果,经分析得表4所示的各偏差源对表征装配质量的关键控制点形变量的综合贡献度。
平等对待每一个关键控制点,经分析得表5所示的各偏差源对右上壁板整体装配质量偏差的贡献度。
5.2 基于熵权法和灰色综合关联分析的右上壁板装配关键偏差源诊断
目前飞机装配采用激光跟踪仪测量装配质量关键控制点的偏差。激光跟踪仪是高精度测量设备,如AT402激光跟踪仪,测量范围内绝对距离测量精度不超过10 μm,绝对距离重复性为5 μm,测量设备引入误差与隔框制造偏差相比可以忽略不计。因此,在本案例中可忽略测量设备引入的测量误差。

表4 各偏差源对装配质量控制点的综合贡献度Tab.4 Comprehensive contribution degree between deviation sources and assembly quality control points %

表5 各偏差源对右上壁板整体装配质量的综合贡献度Tab.5 Comprehensive contribution degrees between deviation sources and right upper panel %
5.2.1基于熵权法的右上壁板装配质量分量权重求解
(1)装配质量多属性评价矩阵构建。依据右上壁板各关键控制点的检测数据,构建右上壁板柔性装配质量多属性评价矩阵A:

(2)装配质量检测数据标准化处理。利用式(2)对多属性评价矩阵A进行标准化处理,得

(3)装配质量分量比重矩阵确定。利用式(3)计算,得装配质量检测数据比重矩阵:

(4)装配质量分量信息熵求解。利用式(1)计算右上壁板装配质量分量的信息熵,得H=[0.85 0.61 0.94 0.98]。
(5)装配质量分量差异性系数求解。利用式(4)计算各装配质量分量差异性系数,得E=[0.15 0.39 0.06 0.02]。
(6)装配质量分量权重求解。利用式(5)计算各装配质量分量的熵权,得Ω=[0.15 0.38 0.06 0.02]。
5.2.2装配质量与其偏差源的关联度量化建模
依据式(6)构建第1个关键测量控制点的分析对比序列x0,x1,…,x12:
式中,x0为参考序列;x1,x2,…,x12为比较序列。
(1)分析对比序列初值化处理。利用式(7)分别对x0,x1,…,x12进行初值化处理,得到新的对比序列(x0)′,(x1)′,…,(x12)′:
(2)装配质量与偏差源之间的灰色绝对关联度求解。利用式(9)分别对(x0)′,(x1)′,…,(x12)′进行始点零化处理,得(x0)″,(x1)″,…,(x12)″:
利用式(12)分别对(x0)″,(x1)″,…,(x12)″关于测量次序积分,得ξ0=13.15,ξ1=-2.38,ξ2=-1.50,ξ3=-0.75,ξ5=-1.25,ξ6=-1.36,ξ7=-1.42,ξ8=-1.00,ξ9=-2.35,ξ10=-2.00,ξ11=-1.93,ξ12=-2.13。
利用式(13)计算各偏差分量和装配质量之间的灰色绝对关联度,得λ01=0.43,λ02=0.45,λ03=0.45,λ04=0.52,λ05=0.48,λ06=0.84,λ07=0.62,λ08=0.59,λ09=0.54,λ010=0.48,λ011=0.46,λ012=0.62。
(3)右上壁板装配质量与装配偏差之间的灰色相对关联度求解。利用式(16)计算各偏差分量和装配质量之间的灰色相对关联度,得γ01=0.47,γ02=0.51,γ03=0.54,γ04=0.59,γ05=0.55,γ06=0.94,γ07=0.66,γ08=0.67,γ9=0.58,γ010=0.46,γ011=0.50,γ012=0.66。
(4)装配质量与偏差源之间的灰色综合关联度。式(17)中,当分辨系数θ取0.5时,灰色绝对关联度和灰色相对关联度所占据的比重相同,关联信息集中。当分辨系数θ小于0.5时,灰色综合关联度倾向于非唯一性,造成结果可比性差;当分辨系数θ大于0.5时,灰色综合关联度不满足规范性,难以保证结果的稳定性。因此,为提高关联系数之间的差异显著性,使关联信息集中,取θ=0.5。利用式(17)计算装配质量序列和装配偏差检测序列之间的灰色综合关联度,得到表6所示的右上壁板各偏差源与关键控制点偏差之间的灰色综合关联度。
5.2.3右上壁板偏差源重要度综合评价
利用式(18),综合熵权Ω和表6,经计算得到装配质量和装配偏差源之间的关联程度:ψ01=0.070、ψ02=0.063、ψ03=0.066、ψ04=0.078、ψ05=0.082、ψ06=0.175、ψ07=0.085、ψ08=0.090、ψ09=0.080、ψ010=0.069,ψ011=0.074、ψ012=0.068。ψ01~ψ012中,ψ06的值明显大于其他值,故影响该壁板装配质量的关键偏差源是第二个隔框的第二个定位点位置度偏差。
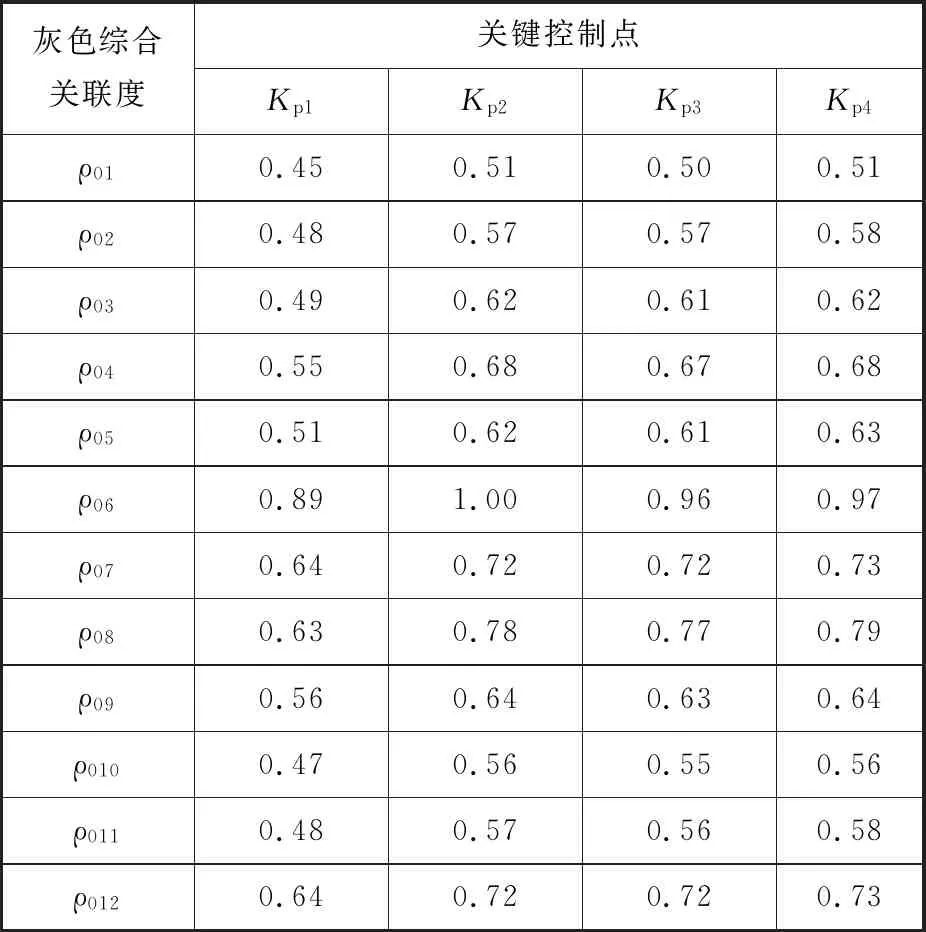
表6 偏差源与关键控制点偏差之间的灰色综合关联度Tab.6 Synthetic grey correlation between deviation sources and deviations of key control points
5.3 3DCS仿真与检测数据挖掘分析对比
综合关键偏差源诊断计算值与基于3DCS仿真结果可得表7。

表7 3DCS仿真与检测数据挖掘的偏差源诊断数据Tab.7 Diagnostic data of key deviation sources using 3DCS simulation and detection data mining %
对比表7中的3DCS仿真数据和本文提出的关键偏差源诊断数据可知:
(1)虽然整张蒙皮的材料和厚度完全相同,各长桁、隔框材料也分别相同,各长桁、隔框均等距安装,各装配件的连接形式也完全一样,但由于该壁板外形是变曲率曲面,使得蒙皮为变曲率薄壁件,隔框外形尺寸不尽相同,导致各偏差源对壁板装配质量的影响程度存在较大差异,波动范围为5.7%~18.1%。
(2)两种方法均得出影响右上壁板装配质量的关键偏差源为F2-P2点的位置度偏差,因此,如果要提高右上壁板的装配精度,减少该点的制造误差可获得较好效果,对指导壁板设计和制造均具有明显的指导意义。
(3)两种方法得出的偏差源重要程度排序存在一定的差异,如F3-P4点。其主要原因是3DCS仿真软件采用均等权重法对装配质量属性进行加权,而本文提出的诊断方法采用了基于挖掘装配质量检测数据潜在信息的熵权法对装配质量属性进行赋权,因此,本文提出的关键偏差源诊断方法更能客观地量化偏差源的重要程度。
(4)工程应用时,本文提出的关键偏差源诊断方法直接依据检测数据进行计算,计算过程直观、简洁,工程意义明晰,避免了黑箱式、复杂的软件仿真过程,也克服了仿真软件自身带来的其他限制与约束。
6 结论
(1)本文针对飞机装配质量与其偏差源之间呈现非线性、多层级强耦合、不确定度大的传递关系,提出一种小样本检测数据驱动的飞机装配质量关键偏差源诊断方法,该方法能客观诊断出影响装配质量的关键偏差源,避免了复杂的建模过程,提高了偏差分析效率。
(2)飞机右上壁板装配案例分析结果表明,3DCS软件仿真和本文所提出的关键偏差源诊断方法的均诊断出影响右上壁板装配质量的关键偏差源为F2-P2点的位置度偏差,但由于DCS软件仿真采用均等权重法对装配质量属性进行加权,而本文提出的诊断方法采用了基于挖掘装配质量检测数据潜在信息的熵权法对装配质量属性进行赋权,使得两种方法得出的偏差源重要程度排序存在一定的差异,因此,本文提出的关键偏差源诊断方法能更客观地量化偏差源的重要程度。
(3)本文提出的小样本检测数据驱动的飞机结构件装配关键偏差源诊断方法具有较好的通用性,可适用于航空航天等各类小批量复杂结构产品的装配质量控制。
