基于鱼骨型仓库的拣选路径问题优化

张新艳， 周雨晴

(同济大学 机械与能源工程学院， 上海 201804)

随着国家经济快速发展，物流产业也呈现快速发展的趋势，而仓储配送是其核心环节.为提高仓储物流管理水平，应对仓储配送环节进行合理优化.2008年Hackman[1]提出有效进行仓储管理主要解决两个问题：一是快速地满足季节性和供应量等需求变化，二是整合和消除不必要的拣货路径.从仓库布局层面来说，设计仓库布局的最新趋势是改变拣选主通道的设计，以便更高效地进行拣选作业.2009年美国学者Gue等[2]提出了鱼骨型仓库布局，并证明相比传统仓库布局，鱼骨型仓库布局可减少约20%的作业路径.2011年Pohl等[3]研究非传统仓库中的货位优化问题，并针对鱼骨型仓库提出了最佳的仓库布局方法.2013年蒋美仙等[4]提出改进的鱼骨型仓库布局方法，并设计最佳仓库布局角度.2015年刘艳秋等[5]基于鱼骨型仓库布局，建立仓储货位分配优化的数学模型，并设计遗传算法求解.2015年Cardona等[6]提出生成鱼骨型仓库布局的三维详细设计方法，并通过寻找4个主要特征值的优化模型来最小化仓库的总运营成本.2016年刘权等[7]提出基于遗传算法的仓库布局优化模型，证明改进后的鱼骨型布局在仓库布局设计中具有更高的可行性和实用性.2017年刘少华等[8]基于鱼骨型仓库布局用遗传算法、蚁群算法和布谷鸟算法对拣货路径问题进行求解.从以上研究可以看出，鱼骨型仓库布局相对于传统仓库布局的优势所在，大部分关于鱼骨型仓库布局的研究都处于仓库设计和仓储货位分配阶段，少有研究涉及到拣货作业.在鱼骨型仓库布局下，由于拣货主通道与子通道之间并非简单的平行或垂直关系，因此用于传统仓库布局下的拣货路径模型不可直接被用于这种新型的仓库布局下.本文将建立在鱼骨型仓库布局下适用的拣选路径优化模型，同时考虑到在拣选车辆以平均速度进行拣选作业时，总作业能耗和总作业时间与总作业距离呈正相关关系，因而在此模型中以总作业距离作为优化目标.

目前常用于拣货路径优化问题的算法有：粒子群算法、模拟退火算法、遗传算法.遗传算法的操作繁杂，需要不断交叉变异，收敛速度慢，易陷入局部最优解.粒子群算法使用简单，收敛速度快，但容易陷入局部最优[9].模拟退火算法全局搜索能力强，但搜索速度慢.为此，2013年刘爱军等[10]提出混沌模拟退火粒子群算法，并将算法应用在车间调度问题中.本文提出采用混沌模拟退火粒子群算法求解鱼骨型仓库布局下路径规划问题，同时在算法的相关参数选择上采取自适应调整的策略，以提高算法的效率和求解精度.

1 问题描述

本文所研究的鱼骨型仓库布局示意图如图1所示.该仓库应用人到货的拣货系统.拣选作业由拣货员操作叉车进行作业，以存取货品点为起点.拣货员从不同的存储位置上收集订单上的货品[11].假设仓库只有一个出入点，每次完成存取作业后都必须回到出入点等待下一次的仓储作业，因此仓库的出入点就是仓库的存取点，简称P&D(picking and deposit)点.该仓库采用的是左右对称的仓库布局，其中有3条拣货主通道，3条主通道都通过P&D点.

1.1 问题参数与假设条件

参数设定如下：W为仓库的宽度；Wr为两侧拣货通道和后部拣货通道的宽度；Wd为两条斜拣货通道的宽度；Wh为存储货格的长度；L为仓库长度的一半；L1为拣货通道的宽度；L2为双排货架的宽度；α为斜拣货通道的角度.

仓库的拣选环境假设如下：

(1) 鱼骨型布局仓库左、右两部分关于中心对称；

(2) 鱼骨型布局仓库拣选通道的排列方式如图1所示，堆垛区1、2、3、4拣选通道数量相等，为m；

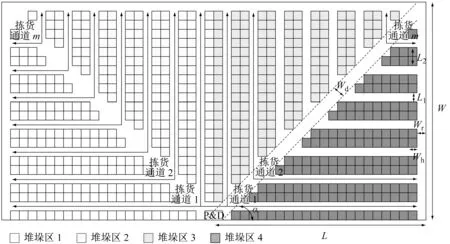
图1 鱼骨型仓库布局

(3) 鱼骨型布局仓库斜拣货通道角度α=45°；每个货格的长度、宽度、拣货通道宽度三者相等，即Wh=0.5L2=L1,Wr=L1;

(4) 拣选车辆在拣选作业开始时从P&D点出发，结束后回到P&D点；

(5) 拣选作业开始之前，满足所有订单的要求，且拣选作业过程中不会发生缺货现象；

(6) 待拣选货物存储于货架之上，货架由货格组成，每个货架的长度和宽度相等，不考虑货架高度；

(7) 拣选距离计算只考虑P&D与待拣货物所在位置的距离，垂直方向上的拣货距离忽略不计；

(8) 拣选距离计算不考虑拣选通道两侧货架的待拣货物所发生的左右移动距离；

(9) 一次拣选订单总量小于拣货车辆最大承载量.

1.2 鱼骨型仓库布局拣货路径模型

基于以上鱼骨型仓库布局的参数设定以及拣选环境的假设条件，本文所建立的拣选路径优化模型如下：

目标函数：

即

(1)

约束条件：

(2)

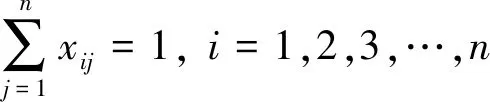
(3)

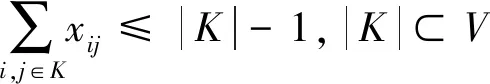
(4)

xij∈{0,1}

(5)

x01=1,xn0=1

(6)

式(1)～(6)中：D为拣选车辆完成一次拣选作业总行走距离；i，j为任意两货位；n为最后一个拣选货位；dij(1≤i,j≤n,i≠j)为货位i到货位j之间的最短距离；d01为P&D点到货位i的拣货距离，即从P&D点开始拣货作业；dn0表示货位i到P&D点的拣货距离，即完成拣货作业回到P&D点.

xij=

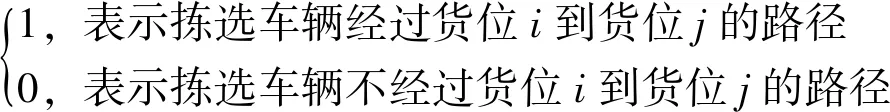
i,j=1,2,3,…,n

目标函数式(1)表示在一次拣选作业中最短的总行走距离；式(2)和式(3)表示所有待拣选点所在货位都被拣选且仅一次；式(4)表示除去未包含某个拣货点的路径，即不存在小回路；式(5)表示货位与货位之间是否存在拣货路径；式(6)表示拣选车辆在进行拣选作业时从P&D点出发，拣选作业结束后需回到P&D点.

1.3 鱼骨型仓库布局拣货距离计算模型

鱼骨型布局仓库中的拣选路径优化问题属于NP难问题，把目标函数设定为拣选行走路径的总距离最短.为计算上述拣货路径优化模型中的d01、dn0和dij，首先，假设任一待拣选点的序号为(s,x,y,z)，其中，s=1,2,3,4表示待拣选物品所在堆垛区的编号；x=1,2,…,X，表示待拣选物品所在的拣货通道的编号，x≤7(本文中鱼骨布局仓库的通道数，如图1所示，共7条)；y=0,1，表示待拣选物品所在通道位置的方位，如果物品在通道的下侧或右侧取y=0，相反，如果物品在拣选通道的上侧或左侧取y=1；z=1,2,3,…,Z，表示待拣选物品在第几个货格里，编号方法为离两侧和后部过道近的货格的编号为1，并依次编号为1,2,3,…,Z.假如待拣选点的序号为(1,2,0,3)，表示的是位于堆垛区1，拣货通道2，下侧的货架，从左侧过道向右数第3个货格.P&D点的位置设为(0,0,0,0)，编码为0.现假设有任意两个拣选点i、j，序号分别为(si,xi,yi,zi)和(sj,xj,yj,zj)，dij表示两点之间的距离.

首先，对d01求解，数字1是指待拣选的第一个货位，可以是待拣选点中的任意一点，此处假设为1点，序号为s1,x1,y1,z1，d01可表示为

(7)

设dn0表示从最后一个拣选点回到P&D所行走的距离，此处假设点n为最后一个拣选点，点n的序号为sn,xn,yn,zn，此时，dn0可表示为

(8)

dij表示任意两个拣选点i、j之间的距离，可表示为

(1) 当i、j两拣选点位于同一拣选通道时，即xi=xj时

dij=|zi-zj|

(9)

(2) 当i、j两拣选点位于不同拣选通道时

xi,xj∈X;zi,zj∈Z

(10)

(3) 当i、j两拣选点位于不同堆垛区内时，分以下4种情况讨论：

① 当i、j两拣选点分布在堆垛区1和堆垛区4两个不同区域内时

xi,xj∈X;zi,zj∈Z

(11)

② 当i、j两拣选点分布在堆垛区1和堆垛区2或堆垛区3和堆垛区4两个不同区域内时

xi,xj∈X;zi,zj∈Z

(12)

③ 当i、j两拣选点分布在堆垛区1和堆垛区3或堆垛区2和堆垛区4两个不同区域内时

xi,xj∈X;zi,zj∈Z

(13)

④ 当i、j两拣选点分布在堆垛区2和堆垛区3两个不同区域内时

xi,xj∈X;zi,zj∈Z

(14)

式(7)到式(14)包含了图1所示鱼骨型仓库布局下任意两拣选点之间距离的求解方法.

2 模型求解

拣货路径规划问题是一个NP 难问题，因此采用PSO (particle swarm optimization)对该问题进行求解.在粒子群算法中，许多粒子被放在某个问题的搜索空间中，以一定的速度在搜索空间探索[12].在一个D维的目标搜索空间中，由N个粒子组成的粒子群落，其中第k个粒子的位置表示为xk=(xk1,xk2,…,xkD),k=1,2,…,N；速度表示为vk=(vk1,vk2,…,vkD),k=1,2,…,N；个体极值是第k个粒子迄今为止搜索到的最优位置，可表示为pk=(pk1,pk2,…,pkD),k=1,2,…,N，适应度记为pbest；全局极值是整个粒子群落迄今为止搜索到的最优位置，可表示为pg=(pg1,pg2,…,pgD),g=1,2,…,N，适应度记为gbest.在每次迭代中，粒子的速度和位置按式(15)和式(16)更新，直到满足最大迭代次数后停止.

(15)

xk←xk+vk

(16)

式中：w表示惯性权重，使其有拓展搜索空间的能力；φ1和φ2表示学习因子，即每个粒子推向pk和pg位置的统计加速项的权重大小；r1和r2是在[0,1]范围内均匀分布的随机数.

为了解决粒子群算法计算过程中振荡与过早收敛的问题，提出SAPSO (simulated annealing particle swarm optimization)，即在粒子群算法中引入模拟退火算法的概率突跳特性，使粒子群算法不但可以接受好的解，也能以一定概率接受不好的解，以提高算法的全局搜索性能[10].为了提高算法的收敛速度，利用非线性自适应惯性权重w(t)代替式(15)中的惯性权重值，其表达式为式(17)，使算法在前期跳出当前极值，在后期较快收敛.为优化粒子种群运动，提高搜索空间的多样性，本文采用混沌理论对r1、r2进行动态调整.用Logisitic模型产生混沌序列[10]公式(18).

(17)

式中:w(t)表示第t次迭代时的惯性权重取值;tmax表示最大迭代次数;t表示当前迭代次数.姜建国等[13]提出wmax=0.95，wmin=0.4时算法性能最优，本文采用此取值.

(18)

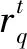
混沌模拟退火粒子群算法的流程如图2所示.

混沌模拟退火粒子群算法的步骤如下：

步骤1 初始化参数设定.最大迭代次数tmax，粒子的速度vk，位置xk，学习因子φ1、φ2，惯性权重w，模拟退火因子φsa.

步骤2 初始化拣货路径.随机生成一系列初始路径集合，用随机模拟方法判断初始路径群体是否满足约束条件式(2)～(6)，以确保种群达到粒子群算法所需规模.

步骤3 粒子群算子操作.按φ1=φ1(1-t/tmax)，φ2=φ2(1-t/tmax)，φsa=φsa×0.97更新学习因子和模拟退火因子，同时按式(15)和(16)更新各粒子的位置和速度.

步骤4 交换序操作.确定个体到个体最优解和全局最优解的交换顺序，混沌产生r1、r2序并和φ1、φ2比较选择执行的交换序，进行交换.

步骤5 计算粒子适应度.针对更新后的新种群计算其适应度函数，即一次拣选作业完成行走总距离，如公式(1)所示，并更新个体的最优位置和最优适应值.

步骤6 模拟退火操作.

① 生成模拟退火初始解S1；

② 插入扰动因子，生成模拟退火的新解S2；

③ 计算新解S2的适应度函数；

④ 判断新解S2的适应度函数值是否小于初始解S1的适应度函数值，若不大于，则用S2代替S1，并转至步骤6；若大于，则以φsa的概率大小接受新解，并转至步骤5；

⑤ 产生伪随机数r，并判断φsa是否大于r.若大于，则用新解S2代替模拟退火初始解S1，并转至⑥；否则，则直接转至⑥；

图2 混沌模拟退火粒子群算法流程图

Fig.2 Flowchart of chaotic SAPSO

⑥ 降低温度；

⑦ 判断当前温度是否达到最低温度.若已达到，则退出模拟退火操作，并转至步骤7.若未达到，则返回①.

步骤7 种群评估与优选.根据个体的最佳适应值，选出种群的最佳位置和最佳适应值，并保存最佳适应值.

步骤8 判断算法终止.若满足最大迭代次数或目标函数减少幅度趋于收敛的预设条件，则输出拣选作业路径总距离以及对应的具体路径方案，算法终止；否则，返回步骤3.

3 仿真及分析

仿真对象为鱼骨型仓库布局，其各项参数取值参见1.1问题参数与假设条件.由于遗传算法的全局搜索能力强，所以选用GAPSO(genetic particle swarm optimization)[14]与混沌SAPSO算法对比，以验证混沌SAPSO算法所得优化结果是否具有全局最优的特点.同时，PSO算法具有收敛速度快的优点，则选用PSO算法与混沌SAPSO算法对比迭代次数与收敛速度.

仿真实验在Inter®CoreTMi5-7300HQ，CPU主频为2.50 GHz、8.00 GB内存、Windows 10操作系统下进行，并利用MATLAB 2016仿真工具编程实现.算法参数设置如表1所示.

表1 PSO、混沌SAPSO及GAPSO算法参数设置

注：S表示初始种群规模；Pc表示交叉概率；Pm表示变异概率.

拣选点样本设置(以10个拣选点为例)如表2所示.

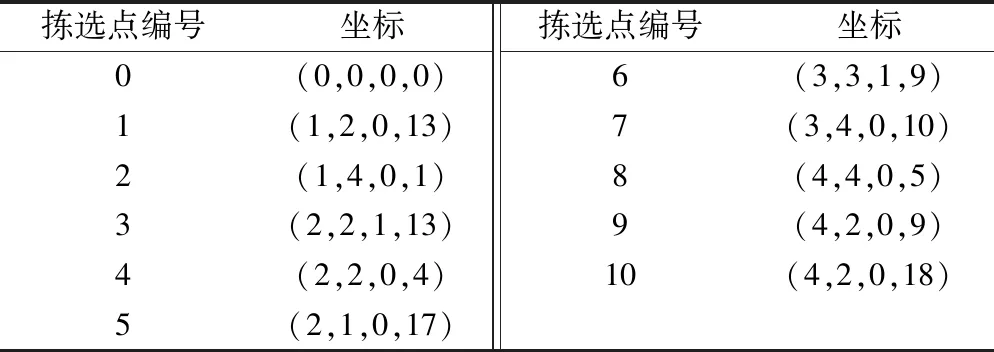
表2 10个拣选点坐标样本

PSO、混沌SAPSO和GAPSO算法对鱼骨型仓库布局下的拣选路径优化模型的求解结果如表3所示.从表中可以看出，混沌SAPSO算法在4种问题规模下的适应度值和收敛速度都要优于PSO和GAPSO算法，可见混沌SAPSO算法避免了PSO算法易陷入局部最优的缺点，同时适应度值比GAPSO算法所求得的结果更优.另外，混沌SAPSO相对PSO平均运行时间在问题规模为10、20、30、40时分别提高了42.01%、10.13%、4.18%、9.29%，混沌SAPSO相对GAPSO平均运行时间分别提高了2.74%、39.50%、54.46%、53.58%.

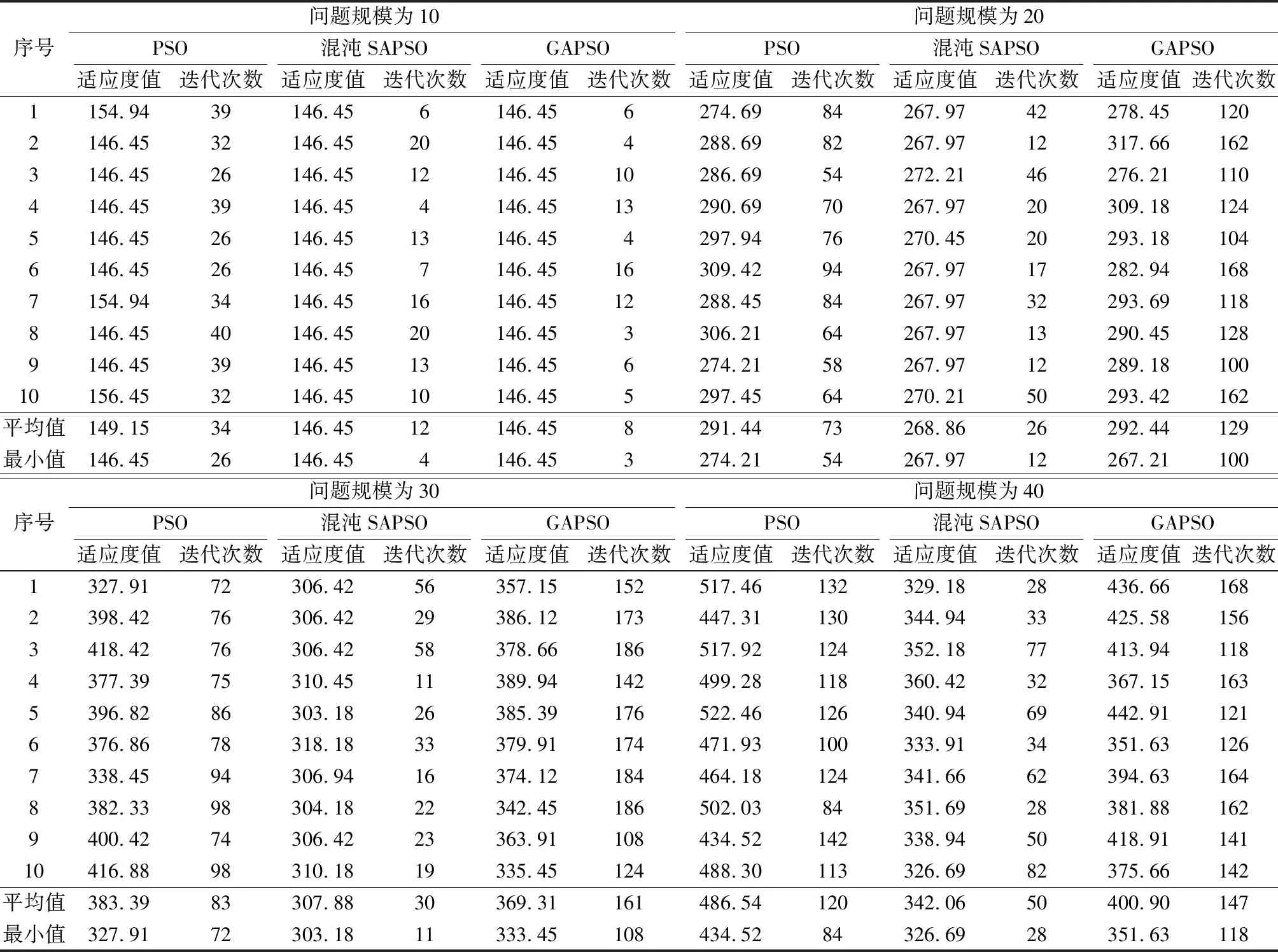
表3 PSO、混沌SAPSO及GAPSO算法的性能比较

PSO、混沌SAPSO和GAPSO算法的适应度曲线如图3所示.从图中可以看出，在4种问题规模下混沌SAPSO算法的收敛速度都比PSO和GAPSO算法要快，同时振荡现象得到了明显改善.

混沌SAPSO算法求解所得路径解的拣选顺序如下：

10个拣选点顺序为0→10→9→8→7→6→4→3→1→2→5→0.

20个拣选点顺序为0→1→11→10→6→7→5→4→3→2→8→9→13→14→16→17→15→18→19→10→12→0.

30个拣选点顺序为0→15→16→5→12→11→9→10→8→6→7→4→3→13→14→23→24→25→22→21→27→26→28→29→30→2→1→20→19→17→18→0.

40个拣选点顺序为0→22→39→40→23→21→24→25→26→36→34→28→27→29→30→31→32→33→35→38→37→2→1→18→3→4→7→6→5→16→14→13→11→9→10→8→12→15→17→19→20→0.以10个拣选点为例，优化后拣货路径示意图如图4所示.

a 10个待拣选点

b 20个待拣选点

c 30个待拣选点

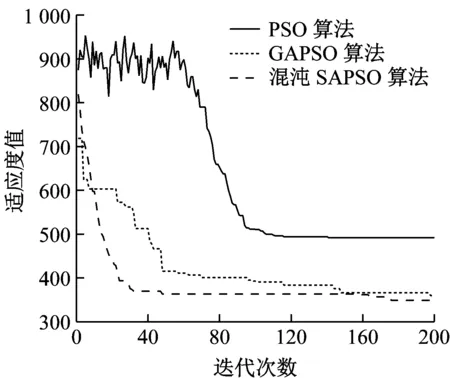
d 40个待拣选点

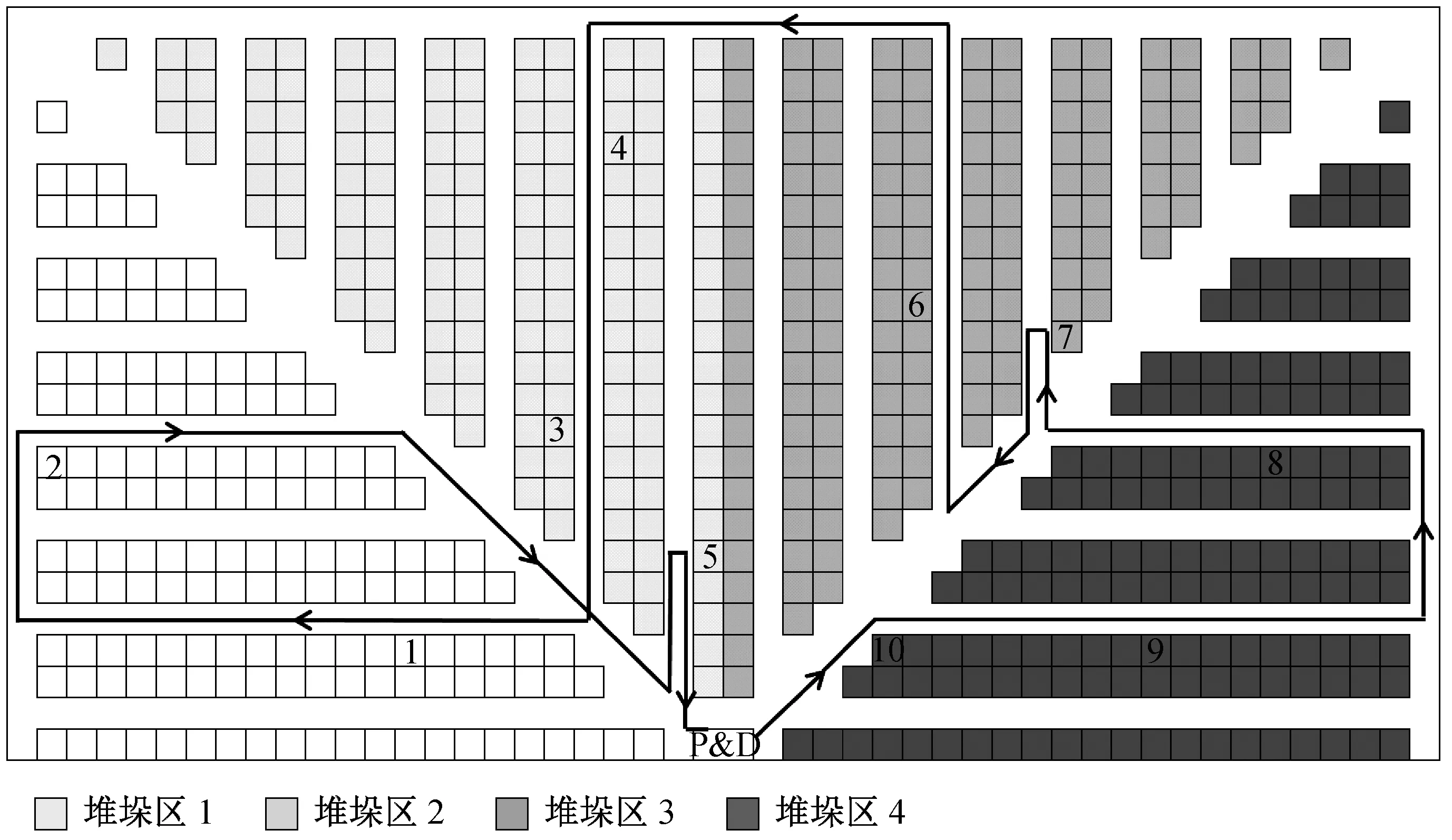
图4 10个拣选点的拣货路径示意图

4 结论

本文的研究基于鱼骨型仓库布局的拣货路径问题，对建立的拣货距离计算和拣货路径优化模型，采用混沌模拟退火粒子群算法进行求解，混沌模拟退火粒子群算法采用混沌理论对粒子群优化算法中的参数r1和r2进行动态调整，同时引入模拟退火算法对粒子群优化算法中的每个粒子位置局部寻优，并设置不同的问题规模，对算法的性能进行了分析.仿真结果表明，混沌模拟退火粒子群算法在适应度值、迭代次数、收敛速度、运行时间和振荡效果方面都优于粒子群优化算法和遗传粒子群算法.

本文的拣货距离计算和拣货路径优化模型可为鱼骨型仓库布局的研究提供决策参考，在后续研究中可进一步考虑鱼骨型仓库布局下的订单分批问题.