斜拉桥H型混凝土桥塔的有限延性

2019-12-02徐艳,童川,2

同济大学学报（自然科学版） 2019年11期

徐艳, 童川,2

(1. 同济大学土木工程防灾国家重点实验室，上海 200092; 2. 同济大学建筑设计研究院, 上海 200092)

我国桥梁抗震设计规范[1-2]要求斜拉桥桥塔在偶遇地震作用下基本保持弹性，而近些年的研究和震害都表明斜拉桥桥塔在强震下存在进入塑性的可能，如1999年即将竣工的集鹿大桥桥塔在集集地震中的破坏[3].针对强震作用下的斜拉桥抗震设计，国外学者已提出在保证抗震安全的前提下，允许桥塔在偶遇地震作用下进入塑性，即利用桥塔的塑性能力进行抗震设计[4].美国的Tacoma大桥[5]和希腊的Rion-antirion大桥[6]都允许桥塔在第二设防水准下出现塑性区域，在利用桥塔的有限延性方面进行了有益的尝试.

近年来，国内也开展了对混凝土斜拉桥桥塔的非弹性地震反应研究.徐艳等[7]对一座典型的混凝土斜拉桥桥塔进行了1/20缩尺比的振动台试验研究，结果表明桥塔的纵桥向具有较高的抗震安全储备，但在强震作用下塔底混凝土依然会开裂，出现裂缝贯通和钢筋裸露的现象.于是徐艳等[8]引入能考虑塑性发展的非线性弹塑性单元，研究纵桥向强震作用下桥梁各主要构件的塑性发展状况及其对全桥地震反应的影响,表明桥塔屈服将显著减小塔柱下部结构的地震需求．徐艳等[9]进一步比较和探讨了斜拉桥桥塔采用常规减隔震设计和非弹性设计的利弊，并对我国典型混凝土桥塔斜拉桥提出了“桥塔有限延性”的抗震设计思想.王瑞龙等[10]和嵇冬冰[11]以一座典型的中等跨度H型桥塔斜拉桥为对象进行了大比例尺(1/20)全桥振动台试验，研究混凝土斜拉桥桥塔在横向地震动作用下的塑性发展过程和破坏行为，试验设计时通过适当降低上横梁配筋率将其作为预设的塑性铰区域，试验结果表明可以通过上横梁的屈服耗能来保证桥塔其他构件基本弹性.曾诗杰[12]以王瑞龙等[10]全桥模型为基础，将“强柱弱梁”的配筋方案改为“强梁弱柱”，通过同比例尺全桥模型振动台试验，对其在横桥向地震动作用下易损截面和破坏模式进行了研究，试验结果表明在“强梁弱柱”的配筋方案下，桥塔的塑性区域及破坏模式均发生了改变，塔柱与下横梁交界的两截面(下塔柱顶部和上塔柱底部)是最易损截面.叶爱君等[13]为研究大跨度斜拉桥倒Y型混凝土主塔横向破坏机理和弹塑性性能，进行了比例尺为1/35的单桥塔模型拟静力试验，结果说明倒Y型桥塔屈服后具有一定的延性能力，最终破坏发生在塔底截面.

由此可见，已有的研究成果虽然针对不同的桥塔形状或不同的配筋设计表现出不同的屈服顺序及易损截面，但都表明了混凝土斜拉桥桥塔在强震作用下具有一定的延性能力，只是尚未确定出可供参考的性能目标及性能指标.为了合理地利用H型混凝土桥塔的塑性耗能能力来减小斜拉桥在横向地震输入下的抗震需求，为斜拉桥的有限延性抗震设计提供理论和试验基础，本文通过有限元分析和拟静力试验相结合的手段对H型混凝土桥塔横桥向屈服后的非线性行为进行研究，初步确定所要达到的性能目标,并得到与之对应的性能指标.

1 动力增量分析

1.1 工程背景

以我国已经建成的某典型中等跨径双塔双索面H型混凝土桥塔斜拉桥为工程原型.该桥主跨采用钢箱梁，边跨采用预应力混凝土箱梁.如图1所示，全桥长640 m，跨径布置为60 m+70 m+380 m+70 m+60 m=640 m.其中,两辅助墩之间主梁为钢箱梁(长520 m)，两侧混凝土梁分别长60 m，桥宽35.5 m，4×12条斜拉索呈扇形布置.斜拉桥桥塔为H型桥塔，塔高91.4 m，桥塔构造见图2.

图1 斜拉桥总体布置图 (单位：cm)

基于OpenSEES平台，建立考虑桥塔弹塑性的精细化非线性有限元全桥模型,其中主塔底部、塔梁交接处(即主塔下塔柱顶部、上塔柱底部)、主塔上塔柱顶部、下横梁以及上横梁均采用纤维截面的梁柱单元建模.

图2 桥塔一般构造图 (单位：cm)

Fig.2 Main tower of cable-stayed bridge(unit:cm)

1.2 地震动输入

以原斜拉桥桥址的场地安全评估报告中提供的50年超越概率5%(E2地震)的设计反应谱为基准,从美国太平洋地震工程研究中心的数据库中选取200条地震动记录，并应用Seismomatch软件在反应谱(周期T=0～2 s)范围内以保证所选地震波在平台段的加速度反应谱值平均值与设计反应谱值基本相等为目标进行筛选，最终确定出的8条地震波与设计反应谱的对比如图3所示.将平台段的加速度反应谱值平均值(Saave)作为IDA(incremental dynamic analysis)分析中的调幅对象，即地震动强度等级(ground motion intensity measure，IM)，如表1所示.

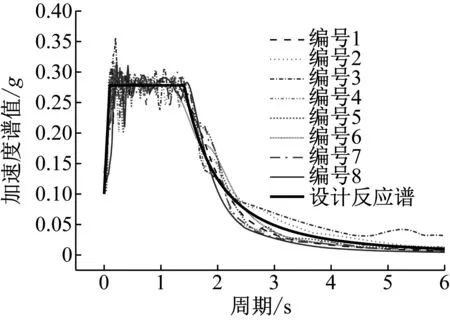
图3 设计反应谱与8条地震动反应谱对比

表1 地震强度等级

注：PGA——地震动加速度峰值.

1.3 H型混凝土桥塔横向破坏全过程

本文将基于IDA方法，通过不断提高地震动强度等级，研究H型混凝土桥塔从弹性阶段至塑性阶段直至最终破坏的全过程.

1.3.1屈服和破坏阶段塔身曲率分布

H型混凝土桥塔在地震动作用下会在塔柱中产生不可忽视的动轴力，而截面曲率的计算与截面轴力密切相关，这也就意味着截面曲率在地震过程中始终处于一个动态的变化过程中.文献[14]指出,动轴力对于截面的首次屈服曲率影响较小，对截面破坏阶段的破坏曲率影响较大.故本文以塔身各截面在恒载轴力下的首次屈服曲率作为判别截面进入屈服阶段的标准，以核心混凝土外侧混凝土达到极限压应变作为判断截面进入破坏阶段的标准，其对应的曲率为破坏曲率.H型混凝土桥塔处于屈服和破坏状态时沿塔身的曲率分布分别如图4和图5所示.

图4 屈服阶段塔身曲率分布

图4中H型混凝土桥塔进入塑性阶段所对应的地震强度等级为3，此时塔底截面首先屈服.图5中H型混凝土桥塔进入破坏阶段所对应的地震强度等级为12，此时上塔柱的底部率先破坏.

1.3.2关键截面钢筋和混凝土最大应变分布

由H型混凝土桥塔的屈服和破坏阶段时的沿塔身的曲率分布可以看出,其最不利截面为塔底截面、下塔柱顶部截面和上塔柱底部截面.主塔屈服由塔底截面控制，而主塔破坏则由上塔柱底部截面控制.图6给出了此3个关键截面在地震动作用下材料最大应变随着地震动强度等级的变化关系.

图5 破坏阶段塔身曲率分布

图6 最不利截面材料最大应变随地震动强度等级变化规律

由图6可知，核心混凝土外侧的钢筋达到屈服拉应变控制着塔底截面的屈服，随后上塔柱底部截面的核心混凝土外侧的钢筋也达到屈服拉应变，接着下塔柱顶部截面的核心混凝土外侧钢筋达到屈服拉应变，而核心混凝土外侧混凝土达到极限压应变控制着各个截面的破坏，H型混凝土桥塔的破坏由上塔柱的底部截面控制.

1.4 关键截面延性能力

钢筋混凝土延性构件的非弹性变形能力来自塑性铰区的塑性转动能力.因此，可采用截面的曲率来反映.

曲率延性系数的定义为

H型混凝土桥塔在地震动作用下会在塔柱中产生较大的动轴力，截面的屈服曲率与动轴力峰值并不是同时达到，当截面达到屈服曲率时动轴力并不是最大值.为了分析的简便，本文将峰值动轴力作为定值来对截面进行能力分析.文献[15]指出，随着轴压比的增大,试件的延性逐步减小.故本文使用峰值动轴力计算得到的曲率延性系数会偏小，计算结果偏于保守和安全，即采用高估了的动轴力状态，对桥塔各个不利截面进行截面分析，可得到各截面的偏于保守的曲率延性能力，如图7所示.

图7 桥塔关键截面的延性能力

由图7可知,桥塔动轴力随着地震强度等级的不断增加而增加，桥塔各个截面的位移延性系数不断降低，随着地震强度等级的提高，动轴力对截面的曲率延性几乎起到决定性作用,即随着动轴力的增加，试件的延性逐步减小.由前文分析可知，塔底截面在IM=3时进入塑性阶段，此时对应的曲率延性系数为21.8;下塔柱顶部截面在IM=5时进入塑性阶段，此时对应的曲率延性系数为17.7；上塔柱底部截面在IM=4时进入塑性阶段，此时对应的曲率延性系数为23.5.新西兰规范[16]中要求，对采用有限延性结构设计的桥梁，曲率延性系数至少取 10；欧洲规范[17]规定其为15，故H型混凝土桥塔利用有限延性能力进行抗震设计的思路是可行的.

2 H型混凝土桥塔横桥向拟静力试验

2.1 拟静力试验方案

考虑到试验条件的限制，本模型决定采用与原型相似比为1∶20，混凝土采用微粒混凝土进行模拟.在本试验选定的配合比下弹性模量相似常数SE=Sσ=0.3，受力主筋和箍筋分别采用φ6钢筋和10#钢丝，其他物理量的相似常数可由量纲分析法得出.

H型混凝土桥塔模型拟静力试验为单向加载，拟静力试验加载布置如图8所示，塔顶竖向荷载恒定并由2个随动作动器施加，单个竖向加载力为3.45 t；下横梁处的竖向力通过张拉预应力的方式来实现，张拉力为5.1 t.水平单向荷载由加载吨位为50 t、100 t、位移行程均为±0.5 m的作动器施加，数据采集频率取5 Hz.

图8 拟静力试验单向加载布置图

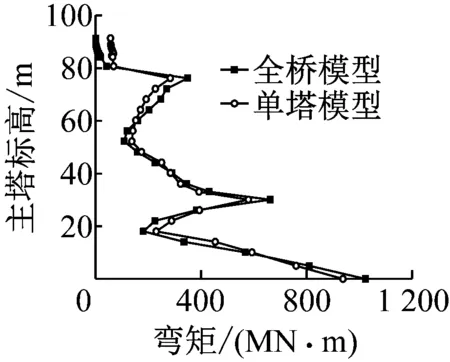
由于拟静力试验无法按照沿塔身的惯性力分布的荷载模式进行加载，而且考虑到当结构进入屈服以后，施加给实际结构的集中力的增加并不明显，即结构响应并不敏感，所以本文采用H型混凝土桥塔上、下横梁处的两点位移加载模式.两点位移加载模式相比原结构的受力有很大的简化，为确保其产生等效的力学行为，简化过程如下：首先通过全桥有限元分析计算得到等效的横桥向单塔模型，其次通过对单塔模型进行不同地震强度等级下的IDA分析，得到不同地震强度等级下的惯性力分布模式，然后对单塔模型进行推倒分析，得到当控制节点达到目标位移时的不同地震强度等级下的上、下横梁位移之比.将此上、下横梁位移比作为两点位移加载模式进行拟静力试验.图9给出了全桥模型和单塔模型在IM=10时(此时结构已进入塑性阶段)的动力反应时程对比，以验证全桥模型等效为单塔模型的正确性.

最终确定的加载方式如下：从上横梁处开始,以幅值3 mm加载至24 mm，上、下横梁位移加载比为3∶1；然后采用幅值1 mm加载至36 mm，上、下横梁位移加载比为1∶2；随后采用幅值2 mm加载至46 mm，上、下横梁位移加载比为2∶1；最后采用幅值5 mm加载至111 mm，上、下横梁位移加载比为5∶1.试验现场如图10所示.

a 位移

b 剪力

c 轴力

d 弯矩

图10 试验现场图

2.2 试验结果分析

2.2.1试验破坏过程描述

试验过程中，当上横梁的位移施加到15 mm时，塔底附近出现裂缝，随着位移的增加，塔底区域裂缝数目扩张；当上横梁的位移施加到21 mm时，上塔柱底部附近出现裂缝，随着试验的继续，该区域的裂缝数目扩张；当上横梁位移增加到32 mm时，下塔柱顶部出现裂缝，随着位移的增加，该区域裂缝和宽度逐步发展.裂缝的发展过程趋势与数值模型的结果基本一致.当上塔顶位移施加到91 mm时，上塔柱底部区域保护层混凝土率先压溃，混凝土剥落，钢筋外露，但塔底截面只是发生裂缝的扩张，保护层混凝土并没有剥落.图11给出了各关键时刻模型的裂缝发展和损伤状态.

图11 试件裂缝发展和损伤状态

Fig.11 Development of crack and damage stage

由H型混凝土斜拉桥桥塔的拟静力试验现象分析可知：拟静力试验中随着横向位移的递增，塔底截面率先出现裂缝，裂缝向上蔓延，接着上塔柱底部出现裂缝，裂缝向上延伸，然后下塔柱顶部区域出现裂缝，裂缝向下延性，即拟静力试验裂缝的发展趋势为塔底—上塔柱底部区域—下塔柱顶部区域；从桥塔破坏状态来看，单塔拟静力试验的破坏由上塔柱底部区域控制，这与有限元的分析结果一致，说明该单塔的加载模式可以在总体上反映桥塔在全桥中的受力行为.

2.2.2试验现象分析及数值模拟

用弹塑性纤维单元建立H型混凝土桥塔单塔试件的数值模型，按照与拟静力试验相同的加载方案进行推倒分析，将所得到的数值结果与拟静力试验结果进行对比分析以确定数值模型的正确性，并借助数值分析的手段进行更深入的研究，以弥补试验手段的不足.

拟静力试验单塔试件的屈服是由塔底截面核心混凝土外侧受拉钢筋屈服控制的，通过试验数据可以发现,当上横梁位移达到35mm时，塔底截面核心混凝土外侧受拉钢筋首次屈服，标志着此时H型混凝土桥塔试件进入了屈服状态.当结构进入屈服状态后，由于钢筋屈服致使应变片温度较高或者脱落，导致试验后期部分应变片数据失效.图12给出了H型混凝土桥塔在屈服之前塔身关键区域受拉钢筋最大应变的有限元数值结果与试验结果的比较.从图中可以看出，两者在上塔柱底部和塔底的误差大部分在10%以内，个别不超过20%，而下塔柱顶部误差较大，但并不影响对屈服状态的判断，可以从中大致观测到塔身关键区域钢筋随着横向位移递增的屈服路径.

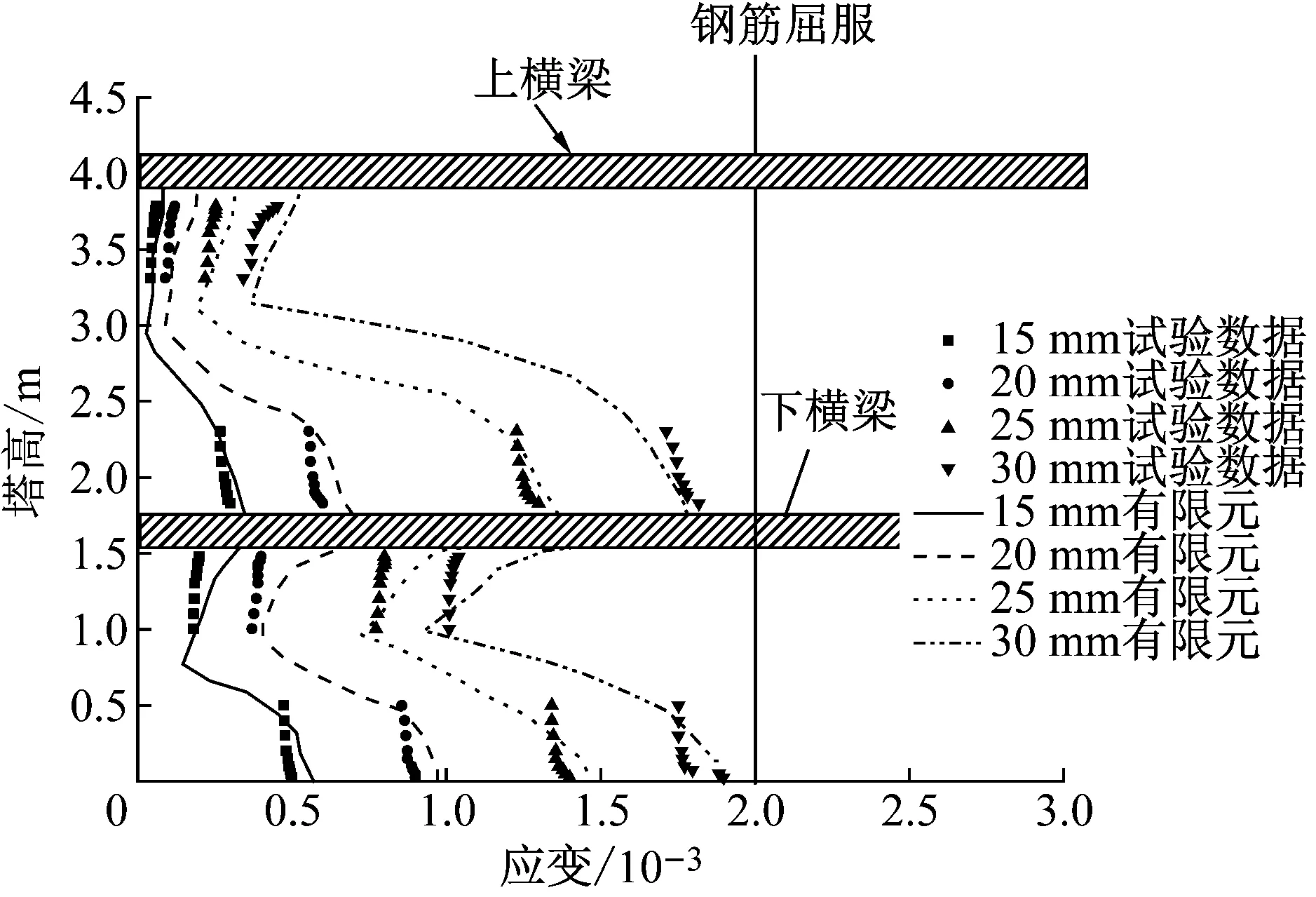
图12 塔身钢筋最大应变分布

由图12的塔身钢筋最大应变变化趋势可以看出:塔身各个关键区域的钢筋最大拉应变随着桥塔横向位移的增加而增加，其中塔底截面附近以及上塔柱底部截面附近的钢筋最大应变增幅尤其明显，这意味着塔底截面和上塔柱底部截面将率先进入屈服状态.在整个横向位移加载过程中截面核心混凝土外侧钢筋的屈服路径应该为：塔底附近截面核心混凝土外侧钢筋率先屈服，然后上塔柱底部截面核心混凝土外侧钢筋屈服，最后下塔柱顶部截面核心混凝土外侧钢筋屈服.

3 性能目标及性能指标的确定

斜拉桥的H型主塔属柔性结构，一般以弯曲变形为主，因而可采用关键截面的曲率作为截面的损伤指标.本文以WSDOT(Washington Department of Transportation)[18]针对Tecoma悬索桥塔柱结构材料应变状态的定义为基础，参考同类文献应变损伤状态的确定方法，定义了基于材料应变状态的截面损伤指标如表2所示.根据该材料应变指标可以求出关键截面对应不同损伤状态的曲率阈值.

在IDA分析中，H型混凝土桥塔的3个关键截面在不同地震强度水平下的曲率需求以及曲率损伤指标如图13～15所示.可以从中看出桥塔关键截面在不同地震强度水平下所处的损伤状态.

表2 损伤状态

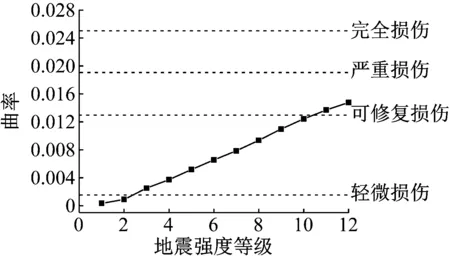
图13 塔底截面包络曲率IDA曲线

图14 下塔柱顶部包络曲率IDA曲线

图15 上塔柱底部截面包络曲率IDA曲线

从图13～15可以看出，在地震强度水平调幅范围内，上塔柱底部截面已进入完全损伤状态，而塔底和下塔柱顶部处于可修复损伤状态.随着地震强度等级的提高，塔底截面率先进入轻微损伤状态，随后上塔柱底部截面和下塔柱顶部截面依次进入轻微损伤状态；上塔柱底部截面率先进入中等损伤状态，接着塔底截面和下塔柱顶部截面依次进入中等损伤状态；最后上塔柱底部率先进入严重损伤和完全损伤状态，但塔底截面和下塔柱顶部截面仍停留在可修复损伤状态.

结合基于材料应变状态的截面损伤指标，图16给出了拟静力试验及有限元数值模拟过程中塔身曲率随着上横梁横向位移增加时塔身损伤状态的变化对比.

图16 塔身各截面损伤状态的变化过程

由图16可知，有限元数值模拟以及试验过程中的关键区域截面的曲率变化趋势整体基本一致，都随着上横梁横向位移增加而增加.其中,上塔柱底部和塔底大部分误差在10%～30%，下塔柱顶部误差相对较大，但不影响对损伤状态的判断.从数值模拟的结果可以看出，当位移达到51 mm时，模型的3个关键截面都已进入轻微损伤状态，分析塔身曲率变化趋势可以推断塔底截面率先进入轻微损伤状态；当位移达到91 mm时，上塔柱底部已率先进入严重损伤状态.在拟静力试验过程中，由现场观测到的现象可知,当位移达到21 mm时，塔底截面出现裂缝；当位移达到91 mm时，上塔柱底部截面出现保护层混凝土压溃的现象，而保护层剥落恰好正是进入可修复损伤状态的特征之一，这时的塔底截面和上塔柱顶部区域出现了裂缝的延伸和扩张，但是没有出现保护层混凝土剥落的现象；当位移达到111 mm时，上塔柱底部截面区域保护层混凝土破坏程度加剧，但塔底和下塔柱顶部截面仍然只是出现裂缝的扩张，钢筋并未露出.

在工程实际中要利用H型混凝土桥塔的有限延性，则需要确保桥塔进入塑性阶段且仅承受可修复的损伤，避免发生严重损伤和完全损伤.由上述分析可知，上塔柱底部截面控制着桥塔的可修复损伤状态.由于H型混凝土桥塔从结构形式上而言类似于两层框架，因此本文尝试从层间位移角的角度去控制桥塔损伤.GB 50011—2010《建筑抗震设计规范》[19]中对钢筋混凝土框架设定的弹塑性层间位移角限值为1/50.利用该规范中的位移角限值可换算得到下横梁相对塔底的相对位移限值和上横梁相对下横梁的相对位移限值.此外，通过原桥IDA分析、模型拟静力试验和有限元模拟也可得到当上塔柱底部截面发生可修复性损伤时，利用相似比换算得到的实桥桥塔上横梁相对下横梁、下横梁相对塔底的相对位移和层间位移角，如表3所示.

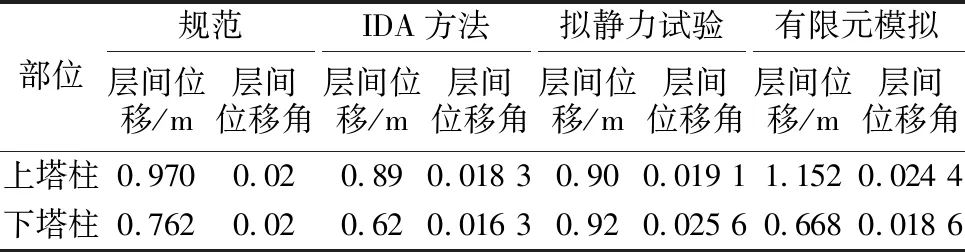
表3 层间位移角限值

偏安全取上述多种分析结果的最小值，据此，本文将可修复损伤作为H型混凝土桥塔的性能目标，将上、下塔柱的层间位移角作为其性能指标，根据原桥IDA分析、模型拟静力试验及有限元数值模拟，并参考文献[19]中对钢筋混凝土框架弹塑性层间位移角限值的规定,最终可确定出：以可修复性损伤状态作为H型混凝土桥塔的性能目标，其对应的材料层面的要求为纵向钢筋应变小于0.55倍极限拉应变，约束混凝土小于0.75倍极限压应变；结构层面的位移角限值为下横梁相对于地面的层间位移角不超过0.016 3，上横梁相对于下横梁的层间位移角不超过0.018 3.但值得一提的是，该性能指标的量值目前还不能直接应用到除原桥以外的实际工程，但本文提供的思路和方法完全可以针对特定的斜拉桥进行计算分析，得到定量的性能指标.针对H型混凝土桥塔的斜拉桥，本文的后续研究工作将可以提供考虑不同轴压比和上、下横梁与塔柱相对高度位置变化的通用性能指标.