积水和降雨下非饱和重塑黄土水分入渗模拟

胡海军， 李博鹏， 田堪良， 巴亚东， 崔玉军

(1.西北农林科技大学 水利与建筑工程学院， 陕西 杨凌 712100; 2.中国科学院水利部水土保持研究所， 陕西 杨凌 712100; 3.法国国立路桥大学 纳维尔研究所岩土力学实验室,巴黎 77455)

非饱和黄土具有显著的水敏性力学特性，即其强度和变形模量与含水率密切相关.黄土滑坡与降雨、灌溉和渠道渗漏等具有很大的关联性.建于黄土地层之上的构筑物在浸水如降雨入渗情况下会产生沉降变形，而计算浸水环境作用下地层水分迁移过程是计算边坡稳定性和地基沉降的前提.降雨入渗是发生最为频繁的地层浸水情况.积水入渗是降雨入渗的极端情况而通常被室内试验所采纳.有关实际降雨情况下的水分入渗，已有大量的试验研究.如,李毅等[1]通过室内试验研究了不同降雨强度下黄土地层的水分迁移规律.基于近似物理模型如Green-Ampt模型的解析方法和求解Richard方程的数值方法是计算积水和降雨入渗条件下土体水分迁移过程的两类基本方法.

基于近似物理模型的解析方法计算简便，特别是考虑浸润锋处吸力合理计算后的Green-Ampt修正模型能较好地模拟积水情况下累积入渗量和时间的关系[2]，却不能较好地计算水分剖面以及实际浸润锋迁移过程.为了模拟积水情况下水分剖面变化过程，王文焰等[3]在Green-Ampt模型基础上提出了考虑积水入渗过程中原状黄土水分剖面形状的入渗模型.本文应用该模型预测重塑黄土积水入渗情况水分迁移过程时，发现由于其不合理地考虑浸润区吸力作用而过快地预测了浸润锋迁移速率；结合Green-Ampt修正模型，本文提出了能合理考虑浸润锋处吸力作用和水分剖面形状的改进模型，并基于Mein等[4]降雨分析理论，将该模型引入到降雨情况下的水分剖面计算.

求解Richard方程的数值方法能严谨求解水分入渗过程，然而非饱和渗透参数的准确选取是影响该方法预测准确度的重要因素[2]，有时不能采用间接法如VG-Mualem模型获得的非饱和渗透系数参数而需要反演[5].基于近似物理模型的解析方法同样存在该问题，鉴于浸润锋前进法[6]或改进的浸润锋前进法[7]能较精确测试非饱和土的渗透系数函数，故本文应用改进的浸润锋前进法来获得非饱和渗透系数函数.

1 模拟方法

1.1 改进模型

1.1.1积水入渗情况

对于积水入渗情况，Green-Ampt模型采用的水分剖面如图1所示，其将实际入渗深度为Zf的浸润体简化为长度为Zs的饱和体，水力梯度采用式(1)计算，根据达西定律得到入渗量增量，该值等于饱和体长度增量下土体水量的增量如式(2)所示，由式(1)和式(2)得到饱和体深度Zs和时间的关系如式(3)所示.

(1)

Ksidt=(θs-θi)dZs

(2)

(3)

式中：i为水力梯度;H为积水水头；Zs为Green-Ampt模型的浸润锋深度(也即饱和体深度)；Sm为Green-Ampt模型浸润锋Zs处的吸力水头(取为正值)；Ks为饱和渗透系数；θi为土体初始体积含水率；θs为土体饱和体积含水率.

图1 积水入渗下Green-Ampt模型、文献[3]模型以及实际的水分剖面示意图

Fig.1 Water content profiles adopted by the Green-Ampt model, the model proposed by Wang Wenyan et al. and the actual water content profile in ponding infiltration

该模型浸润锋处吸力水头Sm并非土体初始含水率θi对应的吸力水头.Philip[8]认为Sm是一个数学量，没有实际的物理意义，该值远小于浸润锋下土体初始含水率对应的吸力水头Si.Bourwer[9]最早给出了Sm的计算公式如式(4)所示，并认为Sm可近似取为增湿过程中进水值,即增湿过程中气不连续时对应的吸力值，然而该值不容易测定，其建议取为饱和样(对应于抽真空饱和样)脱湿过程中进气值的50%，该确定方法比较简单可行[10].在浸润锋以上为饱和的假设下，Mein等[4]应用式(5)获得Sm，该值在初始含水率变化较大范围内相差很小，其对不同初始含水率和不同降雨强度下采用相同的值.Mein等[11]经过推导认为应用式(4)获得Sm是合理可靠的.Neuman[12]通过推导得到了浸润锋处吸力值表达式与式(4)相同.Brakensiek[13]通过比较，表明上述各种方法可得相近的结果.对于采用上述等效吸力的模型称为Green-Ampt修正模型.已有大量研究表明， Green-Ampt修正模型在模拟入渗量和时间的关系上具有较高的准确度[2,14]，说明上述确定Sm的方法有足够精度.从公式(4)可见，Sm小于初始含水率对应的吸力水头Si.

(4)

(5)

式中：Si和Ki分别为初始含水率对应的吸力水头和渗透系数;S和K分别为吸力水头和渗透系数.

Green-Ampt模型及修正模型仅能计算如图1所示的等效饱和体深度.王文焰等[3]根据大量原状黄土现场积水入渗试验中实测水分剖面，假定入渗深度为Zf的区域近似由上部长度为Zf/2的饱和区(严格来讲是传导区，因为饱和区和过渡区的区间都很小[15]，其中传导区和过渡区为接近饱和的区域，所以这里仍用饱和区称之)和下部长度为Zf/2、水分剖面为椭圆的非饱和浸润区组成(见图1)，提出了能计算不同时刻水分剖面的模型，然而在计算浸润锋处等效吸力Sm上却没有采用上述确定方法，其采用下部Zf/2非饱和浸润区平均初始含水率对应的吸力Si施加于上部饱和区底部，得到上部Zf/2饱和区的水力梯度如式(6)所示，根据达西定律和水量平衡原理，得到式(7)，将式(6)代入式(7)整理可得入渗深度Zf和时间t的关系如式(8)所示.如上文所述，作用于长度Zs饱和体的等效吸力Sm小于Si，而将Si作用于长度为Zf/2的饱和区，可见过大估计了下部吸力的作用.该模型[3]计算所得现场积水入渗试验中的水分剖面运移过程较为符合实测，可能在于原状黄土常存在节理和大孔隙，节理[16]或大孔隙[17]存在导渗的作用，加快了浸润锋迁移速率，对此问题应采用相应模型[16-17]进行分析，而不应单独在模型中增加吸力作用.

(6)

Ksidt=0.5(θs-θi)dZf+0.125π(θs-θi)dZf

(7)

(8)

(9)

(10)

式中：ε为浸润区占入渗区的比例，其随Zf的增加而线性增加，可表示为ε=aZf+b.

(11)

(12)

式中：Zs为如图1所示的饱和体长度，按浸润区为椭圆过渡，经过换算Zs=(1-ε+0.25πε)Zf.

Zf=

(13)

(14)

1.1.2降雨入渗情况

对于不同降雨强度下的水分入渗模拟，Mein等应用Green-Ampt修正模型进行了降雨入渗分析[4]，得到与求解Richard方程的数值计算方法相近的入渗率和时间关系，但其并没有引入水分剖面形状来预测实际水分剖面.本文应用上述改进模型，获得实际水分剖面.当降雨强度小于饱和渗透系数时，不会发生径流，入渗率f(t)一直等于降雨强度P.当降雨强度大于饱和渗透系数时，在地表发生径流前，入渗率等于降雨强度；发生径流时，降雨强度P等于入渗强度Ksi，据此可得径流发生时等效饱和体长度Zs，进而根据式(14)得到此时的实际入渗深度Zf；根据此时入渗量Fp等于等效饱和体范围内土体水量变化，可得Fp如式(15)所示，进一步可得径流发生的时刻tp如式(16)所示.径流发生后，假定水及时排走没有积水水头，即发生积水水头为0的积水入渗，入渗量F和时间的关系可按式(17)计算，入渗深度Zf由式(18)和式(14)计算得到.

(15)

(16)

(17)

(18)

1.2 基于求解Richard方程的数值方法

Hydrus-1d软件应用迦辽金有限元法求解给定初始条件和边界条件下的一维Richard方程，获得非饱和土水分迁移过程.一维Richard方程如式(19)所示.对于本文积水和降雨入渗中初始含水率沿深度均相等情况，初始条件如式(20)所示，下边界条件为自由排水边界如式(21)所示.对于积水入渗情况，上边界条件如式(22)所示；对于降雨入渗情况，径流发生前，上边界条件如式(23)所示，当计算到上边界水头为0的时刻，即为径流时刻，从该时刻开始，将上边界条件定义为水头为0的边界，即应用式(22)所示边界条件并将H设置为0；另外还分析了停雨后1 h的水分再分布，该过程将上边界设置为流量为0的边界,即将式(23)所示P设置为0.求解时需要h和θ的关系，以及K与h或θ的关系；然而有时不能采用间接法(如由VG模型持水曲线函数获得的非饱和渗透系数函数)而需要反演计算[5]，本文采用改进的浸润锋前进法[7]进行求取，具体参数确定过程见下文.

(19)

θ(z,0)=θi

(20)

(21)

h(0,t)=H

(22)

(23)

式中：z坐标取向上为正，地表处z=0；此处h为吸力水头，当孔隙水压力为负时取为负值;P为降雨强度.

2 两类模拟方法的验证与分析

2.1 积水入渗情况水分运移计算的验证与结果分析

2.1.1试验情况及参数确定

为检验上述两类模拟方法在模拟重塑黄土积水情况下水分迁移的可靠性，以延安治沟造地工程建设中开挖边坡土料制取的两种干密度重塑黄土土柱积水入渗试验[19]为对象进行模拟.两种土样干密度分别为1.35 g·cm-3和1.53 g·cm-3，土柱初始质量含水率均约为12.5%，初始体积含水率分别为0.174和0.194，积水水头为2 cm，土柱高220 cm.在不同高度处布置水分仪获得了积水过程中的含水率变化，土柱底部为透气板，且入渗速率较慢，浸润锋下的气压阻渗作用可以不考虑.

为了能用上述两类方法模拟试验中水分运移过程，本文测试了饱和渗透系数和持水曲线，各分析方法所需参数如表1所示.其中,间接法1采用室内制取相同初始状态的土样进行增湿或脱湿测试的持水曲线(图2)，应用VG模型如式(24)拟合；对制成相同初始状态的试样进行浸水饱和，应用变水头法测得的饱和渗透系数Ks，应用VG-Mualem模型[20]即式(25)间接获得非饱和渗透系数函数，进而获得Sm.间接法2除饱和渗透系数应用改进的浸润锋前进法根据积水入渗土柱试验获得的饱和渗透系数外，其他参数与间接法1相同.直接法则采用改进的浸润锋前进法[7]根据积水入渗土柱试验获得的非饱和渗透系数函数.

(24)

K=KsΘ0.5[1-(1-Θ1/m)m]2

(25)

图2 实测的持水曲线及VG模型拟合函数

Fig.2 Measured water-retention curves along with VG water-retention functions fitted to independent data

表1 各模拟分析中所需参数

注：① 两种干密度抽真空饱和试样渗透系数分别为6.50×10-5cm·s-1和3.32×10-5cm·s-1，由于浸水饱和试样与一维土柱试验入渗后饱和度接近，渗透系数均采用浸水饱和试样的渗透系数;② 根据浸水饱和试样及一维土柱试验入渗后土柱含水率确定θs，该含水率对应土柱入渗试验中传导区含水率[20],并不是完全饱和的含水率;③ 根据式(5)计算得到两种干密度试样Sm分别为65.6 cm和80.1 cm，鉴于式(4)更为严格，这里仅采用式(4)计算值.

其中应用改进的浸润锋前进法获得非饱和渗透参数的过程如下：根据土柱上各测点含水率开始变化的时间即浸润锋达到该处的时间，按幂函数关系拟合得到浸润锋迁移距离和时间的关系，对于两种干密度试样，所得结果分别如式(26)和(27)所示.应用该关系很容易得到不同时刻浸润锋迁移速率vZf，以其中一个测点A为例，按式(28)计算得到t1～t2时间段通过A断面的水流速度v，浸润锋前进法[12]采用式(29)计算相应水力梯度i，依据改进的浸润锋前进法[7]相应采用式(30)计算t1～t2时间段A断面的水力坡降i，根据达西定律便可得到该时间段平均吸力下的渗透系数，选取不同的时间段便可得到不同吸力下的渗透系数.图3给出了应用改进的浸润锋前进法所得不同吸力下的渗透系数结果.应用VG模型即式(24)，对所得非饱和渗透系数和基质吸力的关系进行拟合，拟合得到的饱和渗透系数在抽真空饱和试样和浸水饱和试样所测渗透系数之间.可见,虽然浸水饱和试样和土柱入渗试验后的饱和度接近，但在渗透系数上仍存在试样不对等性.文献[21]则建议采用入渗试验后的土柱进行渗透试验以获得饱和渗透系数.由于应用式(23)拟合非饱和渗透系数时，所得a和n与原持水曲线拟合参数不同，因此需要在新的a和n下，重新对持水曲线拟合，得到残余含水率θr分别为0.114和0.138，虽然该参数有较大改变，但前后两次所得持水曲线在大于初始含水率时都很接近测试点，而入渗过程是增湿过程，所得持水曲线和非饱和渗透系数函数在含水率大于初始含水率时具有足够的精度.

a 干密度1.35 g·cm-3土柱

b 干密度1.53 g·cm-3土柱

Zf=1.053t0.622

(26)

Zf=0.692t0.592

(27)

[vZf(t1)+vZf(t2)]

(28)

(29)

i(zA,t3)]

(30)

式中：θ(zA,t2)为时刻t2、深度zA处测点A的体积含水率；Ψ为基质吸力，由前面所测持水曲线拟合函数根据含水率反算得到；vZf为t1～t2时间段浸润锋迁移速度.

2.1.2模拟结果分析

图4给出了各方法所得浸润锋入渗深度和时间的关系以及与实测结果的对比.总体上，王文焰等提出的模型[3]过快地预测了入渗过程，Green-Ampt修正模型较慢地预测了入渗过程，而采用相同参数情况下改进模型较Green-Ampt修正模型提高了浸润锋迁移速率，相比前两种方法均更加接近实测值.针对采用不同方法确定的参数，采用间接法1所得参数误差较大，而采用间接法2或直接法所得参数预测结果均较为接近实测值，说明饱和渗透系数的准确性在很大程度上决定了预测的准确度.另外整体上，对干密度1.53 g·cm-3土柱预测较为准确，这可能与1.35 g·cm-3土柱具有导渗的大孔隙有关.

a 干密度1.35 g·cm-3土柱

b 干密度1.53 g·cm-3土柱

图5给出了土柱不同深度测点体积含水率随时间变化的实测与预测结果.本文改进模型和Hydrus软件数值方法都能模拟出浅部测点体积含水率变化快，深部测点体积含水率变化稍慢的特点.总体上，对于干密度1.53 g·cm-3土柱预测较好，而对干密度1.35 g·cm-3土柱预测稍差.

a 干密度1.35 g·cm-3土柱

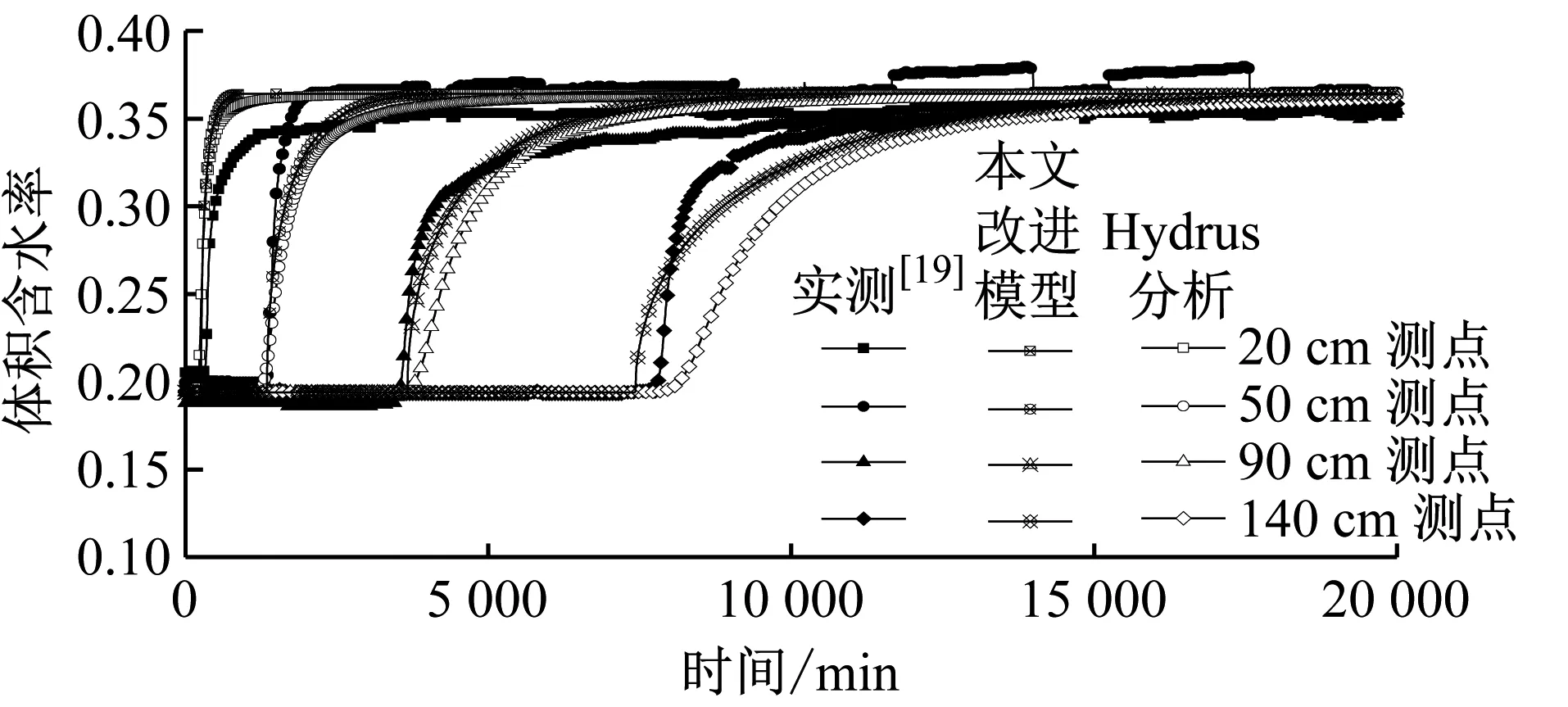
b 干密度1.53 g·cm-3土柱

图6给出了浸润锋到达各测点时的水分分布预测值和实测结果的对比.本文改进模型和Hydrus软件数值方法所得结果很接近，只是在浸润锋位置处稍有差异.有限的实测点结果接近于两种方法所得的水分分布线，说明两种方法的可靠性.另外,根据Hydrus软件所得结果，分析水分剖面从饱和到非饱和的过渡点，得到饱和区(严格来讲为传导区)所占比例随着入渗深度的增加由0.3变化到0.6.

a 干密度1.35 g·cm-3土柱

b 干密度1.53 g·cm-3土柱

图6 积水入渗过程浸润锋到达各测点时的水分分布预测值和实测结果对比

Fig.6Comparison of predicted and measured water content profile when wetting front arrived at measurement points in ponding infiltration

2.2 降雨入渗情况的验证与分析

为了获得积水入渗和降雨入渗的差别以及本文改进模型相对于Green-Ampt修正模型在降雨入渗过程分析的适宜性，对比了Green-Ampt修正模型、本文改进模型和Hydrus软件数值方法所得降雨情况下浸润锋入渗规律和水分剖面，并与积水情况进行了对比.

结合取土地区的降雨情况资料[22]，本文选取特大暴雨1.170 cm·h-1、大雨0.208 cm·h-1和中雨0.104 cm·h-13种雨强下降雨24 h和停雨24 h作为分析情况.对于Green-Ampt修正模型和本文改进模型，按式(16)计算得到干密度1.35 g·cm-3和1.53 g·cm-3土柱仅特大暴雨情况下分别在3.4 h和0.73 h发生径流，其他两种雨强在24 h内均未发生径流；Hydrus分析结果表明24 h内也仅特大暴雨下发生了径流，径流时间分别为4.5 h和0.8 h，这与Green-Ampt修正模型和本文改进模型所得结果相近.

图7给出了积水和3种雨强条件下浸润锋入渗深度和时间的关系.对于Green-Ampt修正模型和本文改进模型，径流之前，由于土柱表面处于非饱和状态不能应用改进模型预测，图中仅给出了径流发生后的入渗深度和时间的关系.从结果上可见，本文改进模型比Green-Ampt修正模型更加接近Hydrus所得结果.对比3种雨强和积水入渗结果，特大暴雨情况比较接近于积水入渗情况，特别是干密度为1.53 g·cm-3土柱.这也说明了积水入渗可以作为降雨入渗的极端条件予以研究.

a 干密度1.35 g·cm-3土柱

b 干密度1.53 g·cm-3土柱

图7 降雨24 h过程中入渗深度和时间的关系以及与积水入渗的对比

Fig.7 Infiltration depth versus time during 24 h rainfall compared with that under ponding condition

图8给出了特大暴雨情况下，在降雨24 h和停雨24 h时间段，两种干密度土柱水分入渗及水分再分布过程水分剖面图.Hydrus分析结果表明，初始入渗时土柱表面由非饱和状态逐渐过渡到饱和状态，Green-Ampt修正模型和本文改进模型不能预测径流发生前的水分分布变化；发生径流时及降雨24 h时，本文改进模型所得水分分布与Hydrus所得水分分布接近，特别是干密度1.53 g·cm-3土柱，而Green-Ampt修正模型预测水分剖面精度较差.相对于降雨24 h，发生径流时Green-Ampt修正模型和本文改进模型所得结果与Hydrus分析结果差异较大.这主要是由于径流发生的时间不同导致两者入渗量不同，另外如前面分析表明入渗深度浅时，饱和区所占比例小，改进模型在此阶段采用了相对较大的饱和区比例.降雨结束后，改进模型不能预测水分重分布，Hydrus分析得到土柱表面含水率减少并且更深处水分增加，这与已有实测规律[1]相符.需要说明的是，该分析过程宜采用增湿后脱湿的持水曲线函数，另外停雨后一般涉及到蒸发，需要测试或计算蒸发强度E，此时可将式(23)中P替换为-E的上边界条件进行计算.

a 干密度1.35 g·cm-3土柱

b 干密度1.53 g·cm-3土柱

3 结论

在Green-Ampt修正模型和王文焰等提出的模型[3]基础上，提出了可较为合理预测入渗过程中水分剖面及迁移过程的改进模型，应用各模型和求解Richard方程的数值方法模拟了室内重塑黄土积水入渗试验，并对比了特定雨强下本文改进模型和数值方法所得的水分剖面.主要结论如下：

(1) 本文改进模型合理考虑了浸润锋处吸力作用和水分剖面形状，相比Green-Ampt修正模型和王文焰等提出的模型，能更好地模拟室内非饱和重塑黄土积水入渗试验中水分迁移过程.

(2) 根据土柱入渗试验各测点水分变化，采用改进的浸润锋前进法[7]获得的饱和渗透系数和非饱和渗透系数函数时，能较好地预测水分迁移过程，而采用室内制样获得的饱和渗透系数和间接法获得的非饱和渗透系数函数时预测误差较大.

(3) 根据文献[4]提出的降雨入渗理论，将改进模型推广到降雨情况下径流发生后的水分剖面预测，所得结果与求解Richard方程的数值方法分析结果接近，特别是在试样干密度比较大的情况，改进模型相对数值方法计算简便、易于应用.另外,应用Hydrus软件可以分析得到径流发生前和停雨后的水分迁移变化过程，结果与已有试验规律相符，显示出较强的模拟能力.