机非交互路段非机动车越线超车行为建模与仿真
2019-12-02刘启远
刘启远, 孙 剑, 田 野, 倪 颖
(同济大学 道路与交通工程教育部重点实验室, 上海 201804)
非机动车越线超车行为是机非交互路段较为典型和复杂的驾驶行为[1],同时随着近年来电动车使用量的增长[2],导致此类行为事件的发生频次增加[3].准确地对机非交互路段非机动车越线超车行为进行建模,对机非交互车道的安全评价、通行能力分析、管控方式设置以及智能驾驶车辆的辅助决策等方面均具有重要意义[4-7].
非机动车越线超车行为具有交互对象多样(含电动车、自行车、机动车等)、交互过程复杂(包括超车动机产生、接受超车间隙、超越目标车辆、持续占用机动车道自由行驶、主动选择返回间隙、返回非机动车道等过程)两个典型特征[8],并且受驾驶者个人特征影响显著.目前学者大多关注车辆的超车动机、超车及返回原车道间隙大小判断,侧重于越线超车频次等指标的分析[1,4-5,9],超越目标车辆前、后的越线时间一般较为接近.而实测数据表明,在电动车比例较高的非机动车流中,非机动车在超车后的越线持续时间远大于超车前的越线持续时间.此因素导致非机动车的超车时间预测存在如下难点:① 影响越线超车持续时间因素复杂,即返回动机既受到相邻车道的机动车影响,也会受到周边其他非机动车状态的影响,即使在有返回间隙的情况下,也会有一定的越线超车车辆持续占用机动车道;② 中高密度情况下越线车辆的从众效应,以及越线超车车辆的自身速度等因素,均会影响非机动车辆持续占用机动车道时间,此类影响因素难以准确量化;③ 即使在较长观测区间,仍有部分越线超车车辆持续占用机动车道,此部分数据的处理对准确描述越线超车行为具有重要影响.
另一方面,由于越线超车为随机事件,在越线事件中,仍存在观测范围内非机动车辆未返回原非机动车道的实例,导致越线超车存在一定量的删失数据,如何合理有效利用样本数据是模型构筑的关键.近年来应用越来越广泛的生存分析,可以有效考虑信息相对缺失的非完全数据以及超出观测区间的删失数据,被广泛应用于生物统计、医疗等领域,目前逐步被引入交通运输领域,在交通流瓶颈失效持续时间,行人最大可忍受过街等待时间等方面得到一定的应用[10-11],其在数据存在删失以及受多因素影响的不确定事件预测,具有较强优势.
基于此现状,本文建立了基于生存分析的越线行驶时间预测模型,在此基础上整合了纵向跟驰行为模型、变道动机模型及可接受间隙模型等,对非机动车超车行为进行建模与预测;进一步构建了系统的非机动车越线超车全过程仿真模型,并将模型应用于自主研发的微观交通仿真系统TESS NG(Tongji nEtwork simulation system next generation)中.最后以总的越线持续时间等为指标,与VISSIM仿真系统进行了效果对比评价.
1 模型构建
1.1 基于虚拟车道划分的模型构架
在机非交互路段中,机动车道与非机动车道间存在软隔离车道线.为了高效准确地描述非机动车的越线超车过程及交互对象,本研究将机非交互空间划分为准二维的虚拟车道空间(单个虚拟车道宽度为0.8 m且参数可调).非机动车与机动车在虚拟车道间进行变道、超车.在非机动车越线超车的整个行为中,一般会有3个过程:① 越线开始至超越目标车辆;② 超越目标车辆后的越线自由行驶过程;③ 开始主动选择间隙返回原车道.非机动车道一般具体划分方式及越线超车的过程如图1所示.

图1 非机动车越线超车行为说明
1.2 越线超车时间组成
在非机动车越线超车的总过程中,车辆超车的总时间为
T=t1+t2+t3
(1)
式中:T为非机动车越线超车的总时长;t1、t2、t3分别为图1中越线超车3个过程的越线时长.则对于任意的超车车辆i超越车辆j时,设其运行的所有时刻为ti,其开始越线时刻ti,0,超越目标车辆j的时刻ti,1,开始执行选择间隙返回原车道时刻ti,2以及返回非机动车道时刻ti,3,上述4个时刻分别定义如下:
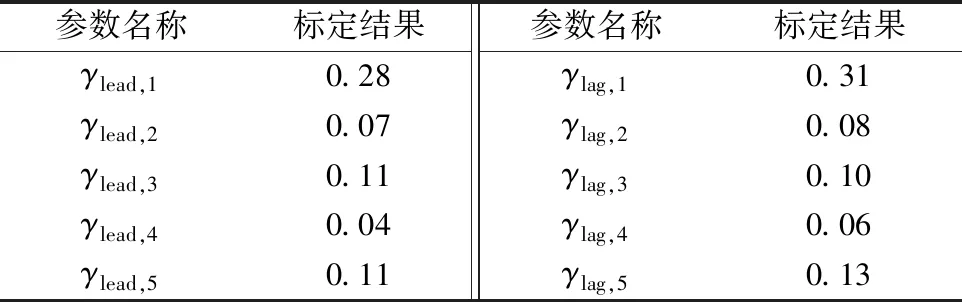
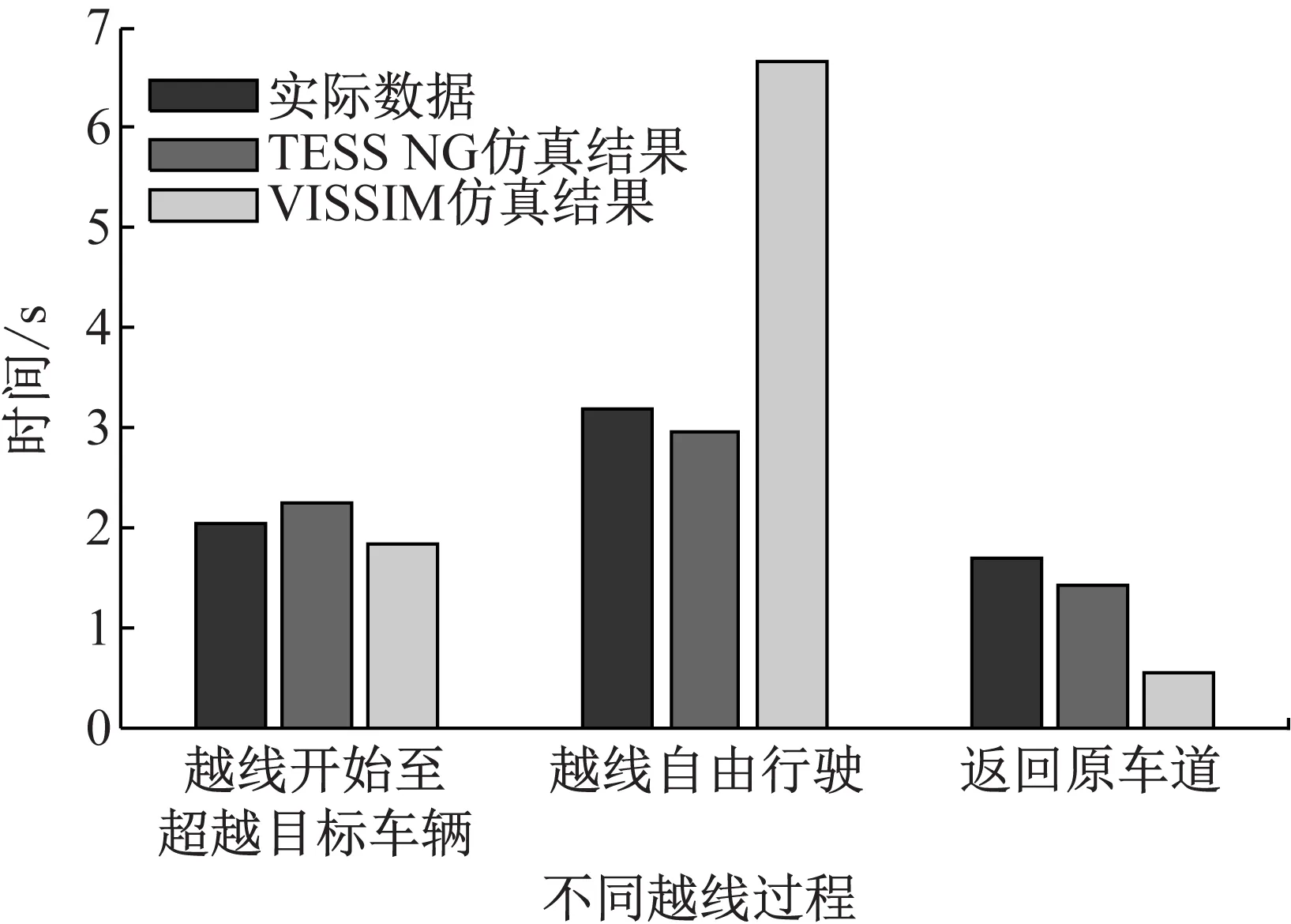
ti,0={ti|yi,t-1 (2) ti,1=min{ti|xi,t-1 (3) ti,2= (4) ti,3={ti|yi,t-1≥Y,yi,t (5) 式(2)~(5)中:xi,t-1、xj,t-1及xi,t+1、xj,t+1分别为非机动车i和j在沿行驶方向t-1及t+1时刻的横向位置;yi,t-1、yi,t、yi,t+1分别为非机动车i在t-1,t及t+1时刻垂直行驶方向的纵向位置;Y为机非隔离标线所在的纵向位置;ai,t为非机动车i在t时刻的瞬时加速度;ai,t4为返回原车道时刻的加速度;ax、bx分别为车辆开始选择前、后间隙时横向临界加速度绝对值;ay为车辆选择当前间隙纵向临界加速度绝对值[12].ti,0、ti,1、ti,2及ti,3一般满足下式: ti,0 (6) 当ti,1=ti,2时,表明越线超车非机动车在超越目标车辆后立刻执行返回原非机动车道决策. 非机动车辆在超越前方非机动车辆时,一般处于无前方车辆影响时的自由、加速状态,或受当前虚拟车道前方机动车、非机动车影响的跟驰状态,其加速度计算公式如下: (7) 式中:ai为非机动车i的期望加速度;vi为非机动车i的期望速度;vi,t表示车辆i在t时刻的瞬时速度;af为非机动车跟驰或超车时受所在虚拟车道前方的机动车、非机动车影响时的加速度大小.为了建模有效性及便利性,机动车及非机动车的跟驰加速度计算均采用IDM(intelligent driver model)模型[13],其计算公式如下: (8) (9) 式中:S*(vi,t,Δv)表示跟驰前车时的期望跟驰距离;Sa为当前虚拟车道的实际跟车距离;S0为安全停车距离;Ti为车辆的跟车时距;Δv表示车辆i与跟驰前车前速度差;ai与bi分别为期望加速度和期望减速度;α和β为待标定参数. 当非机动车越过目标车辆后,受当前虚拟车道前方或后方车辆影响时,会让行后方机动车或避让前方车辆,其返回原车道的动机可定义如下:受前方车辆影响时 {vi,t|vfm,t (10) {(xi,t,yi,t)|xfm,t-xi,t (11) 受后方车辆影响时 {vi,t|vi,t (12) {(xi,t,yi,t)|xi,t-xrm,t (13) 式(10)~(13)中:vfm,t、vrm,t分别为超越目标车辆后,所在虚拟车道前方车辆和后方车辆的当前速度;xfm,t、yfm,t分别为虚拟车道前方车辆的横、纵向位置;xrm,t、yrm,t分别为虚拟车道后方的车辆横、纵向位置;ds、dl分别为影响横、纵向界限.即非机动车受到当前前方车辆干扰或自身阻滞后方车辆运行时,会主动返回原非机动车道. 而在更多的情况下,非机动车越线超车时前、后方一定范围内均不受机动车干扰,此时为了准确预测t2所占用的时间,这里采用生存分析法来分析车辆的越线生存时间. 在生存分析中,有如下相关6类定义表征了研究事件的特征:① 起始事件——反映研究对象开始生存的起始特征事件.在非机动车越线超车的过程中,非机动车开始越线即为起始事件.② 死亡事件(终点事件)——出现研究者关注的终止事件.在观测路段的整个过程中,非机动车返回原非机动车道即为终点事件.③ 观察时间——从研究开始观察到观察结束的时间,即观测在路段中非机动车运动全过程时间.④ 生存时间——观察到对象存活时间,即非机动车的越线时间.⑤ 完全数据——从观察起始事件到死亡事件所经历的时间,生存时间是完整的.⑥ 删失数据——生存时间是不完整的,事件不是由于终点事件而结束的,而是由于失访、观察时间结束而对象仍存活等原因产生的.由于在机非交互路段的观察区间内,非机动车会在任意时刻产生越线超车,同时在路段观测中,无法观测整条路段(并且即使完全观测整条路段,也有非机动车辆直至路段结束或驶至交叉口也未返回非机动车道而成为删失数据),所以研究观测会在某个位置截止.而研究截止时,观测的越线超车非机动车没有返回原非机动车道的事件即为删失数据,记为0;,将观测结束时已返回原非机动车道的样本数据(终止样本)记为1. 假设S(t2)为车辆决定持续自由行驶的生存时间大于给定某时间t的概率,即生存函数;F(t2)为死亡函数,则有 (14) 式中:f(t)为其自由行驶持续生存时间的概率密度函数.风险概率h(t2)即在此时间t2时刻发生事件的概率,即 (15) 式中:T2为生存时间从0到最大值的分布;Δt为数据分析的时间间隔.同时由于在非机动车的实际应用中,Δt即为统计的非机动车轨迹点的间隔.h(t2)在实际计算时,一般采用下式: (16) Nr,T2=NT2-0.5Nd (17) 式中:Nd为删失的越线非机动车数据.在进行生存分析时,Nd的比例一般不宜过高. 在生存分析中,由于时间变量t2一般不满足正态分布和方差齐性的要求(存在删失数据),采用一般的线性回归方法无法准确分析生存时间与影响因素之间的关系.在生存分析的应用中,Cox风险比例回归模型[14]不需要事先知道生存时间的分布,通过分析多个危险因素对生存时间的影响,即可以建立生存时间与危险因素之间的关系,属于一种半参数模型.采用此种方法,越线超车的持续生存时间风险模型h(t2/X)可定义为 (18) 式中:h0(t2)为基础的风险方程;Xi、αi分别为影响生存时间的风险因素及参数;X为总的因素;m为影响因素的个数.在某个独立因素影响下的生存时间风险为 h(t2/Xi)=h0(t2)exp(αiXi) (19) 本研究选择的影响因素包括越线超车瞬间的机动车道及非机动车道的其他非机动车辆位置及状态详细信息,共计7个影响因素:X1超车车辆速度,X2被超车车辆速度,X3超车时的速度差,X4超车时前方影响范围内非机动车道内的车辆数,X5超车时前方影响范围内越线的非机动车辆数,X6当前虚拟车道的前车距离,X7当前虚拟车道前车速度. 在某种因素Xi下,个体持续时间风险相对于基础风险比例大小R(t2)可定义为 R(t2)=h(t2,X)/h0(t2) (20) 在此基础上,车辆超车的生存时间t2为 (21) 式中:S0(t2)为基准生存概率,即相关自变量在无因素影响时的非机动车越线持续时间概率,其一般服从负指数分布. 接下来在构建可视化仿真系统时,建模还需要考虑非机动车辆的超车动机模型及间隙选择模型,用以完善超车过程描述,具体如下. 1.5.1变道动机模型 建模时引入了现有研究较为成熟的变道动机模型及间隙接受模型,其中变道动机模型的具体形式如下[15]: {vi,t|vf (22) 式中:vf为当前虚拟车道的前车速度.即当前车速度小于当前车速,并且当前车速小于期望速度时,非机动车产生变道动机. 1.5.2间隙选择模型 车辆的间隙选择模型采用NGSIM(next generation of simulation)的非线性可接受间隙模型[16],并采用实测数据进行标定.同时在原有模型基础上,模型中增加了车型对接受间隙的影响,间隙接受的具体模型形式如下式: Gλ,i=exp[γλ,1+γλ,2max(0,Δvλ,i)+ γλ,3min(0,Δvλ,i)+γλ,4vλ,i+γλ,5Tλ,i], λ=lead或lag (23) 式中:Glead,i、Glag,i分别为超车非机动车在虚拟车道超车及返回原车道时的可接受前、后方临界间隙;Δvlead,i为非机动车i与间隙前方车辆的速度差;Δvlag,i为间隙后方车辆与非机动车i的速度差;vlead,i及vlag,i分别为接受间隙前、后的车辆速度;Tlead,i、Tlag,i分别为间隙前、后方车辆类型;γlead,1、γlead,2、γlead,3、γlead,4、γlead,5、γlag,1、γlag,2、γlag,3、γlag,4、γlag,5均为待标定参数. 研究选择了上海市典型机非交互车道,即曹杨路(武宁路至枫桥路段)100 m的机非交互车道进行分析.此路段机非车道为软隔离标线分隔,非机动车道宽度为2.8 m,单个机动车道宽度为3.5 m.高峰期的越线超车行为频繁,是研究非机动车越线超车行为较理想的路段.本研究采集了晚高峰2 h(16:30—18:30)的数据进行分析,前1 h数据作为标定数据,后1 h作为验证数据.分析前,利用George软件[17]提取了路段上所有机动车与非机动车的轨迹数据.轨迹精度为0.1 m,时间颗粒度为0.12 s,数据精度可以应用于非机动车越线行为的特征分析.轨迹提取视频画面如图2所示. 图2 机非交互路段车辆轨迹提取画面 在2 h的数据中,非机动车通过共计1 256辆,其中电动车占比为83.60%.非机动车发生越线超车现象共312次,其中电动车占比为100%,没有自行车出现越线超车的现象.312辆越线超车非机动车中共计252个非机动车返回非机动车道,占比为80.77%;其他19.23%的越线超车非机动车在观测区间内持续占用机动车道,即删失数据. 在越线时间特征指标上,超车前的平均越线时间为2.04 s,超车后的平均越线时间为4.76 s.超车后的越线持续时间是超车前的2.33倍,超车前、后的越线时间体现出了较强的非对称性. 在构建的越线超车模型中,部分参数为直接观测参数,统计后可直接应用于模型.统计的机动车、非机动车基本观测参数如表1所示. 表1 基本参数统计表 2.4.1非机动车跟驰模型参数标定 由于机动车仅在机非交互路段执行基本的跟驰行为,无停车变道等驾驶行为,其模型参数对本研究影响较小,故仿真中仅需要设置其期望速度即可.研究重点关注非机动车的模型参数.本研究采用正交试验及遗传算法对非机动车运行的跟驰及变道模型参数进行标定,在跟驰模型中,以车辆在路段的运行总时间与仿真时间一致,对跟驰模型的式(8)、式(9)中4个参数S0、Ti、α及β进行标定,车辆的期望加、减速度由表1的观测参数得出,标定的仿真步长为0.125 s,标定时的目标函数Z(t)为 (24) 式中:N值为158,即标定时的车辆数目;ti为实际采集100 m范围的车辆运动时间;ts,i为仿真环境中的车辆运行时间.当迭代时的平均目标函数改变值小于0.01%时,迭代终止.最终跟驰模型的参数标定结果如表2所示. 表2 非机动车跟驰模型参数标定结果 2.4.2非机动车变道模型参数 标定变道模型时,同样采用正交试验及遗传算法,本研究为便于计算,将超车时变道至机动车道的间隙及返回非机动车道的间隙统一标定,由于向机动车道变道时前、后方接受间隙车型会出现机动车,故两者的差异性通过车型Tlead,i及Tlag,i体现(非机动车取值为0,机动车取值为1),共标定γlead,1,γlead,2,γlead,3,γlead,4,γlead,5,γlag,1,γlag,2,γlag,3,γlag,4,γlag,510个参数.标定时的目标函数如下式: λ=lead或lag (25) 式中:Gλ,i,s为不同参数下的前、后方间隙大小;Gλ,i为实际的前、后方间隙大小;Nλ为实际采集的接受前后方间隙数目,标定的参数结果如表3所示. 表3 非机动车变道模型的参数标定结果 2.4.3危险函数的参数标定 在对生存函数的相关参数进行标定时,本文利用SPSS中Forward LR向前筛选的方法,对生存分析的参数进行估算.通过迭代,最终筛选出影响自由情况下的非机动车越线持续时间的两个因素分别为:X1超车车辆速度,X5超车时前方影响范围内越线的非机动车辆数.参数评估如表4所示. 表4 危险函数参数估计结果 表4中,B为危险函数式(19)的αi的参数值,SE为系数标准误差,Wald为卡方值,df为自由度,Exp(B)为此因素的相对危险度,最后一列为相对危险度95%置信区间的上下界.由表中结果可知,两个因素的最大值Sig.均小于0.05,表明两个因素均为越线的显著影响因素.B均小于0,说明两个因素均对生存时间的危险程度具有负影响.即超车车辆速度越快,其在线外自由行驶的时间越长;同时前方越线的非机动车辆数越多,超车车辆自由行驶的时间越长,表明非机动车具有一定的从众效应.此特点在其他非机动车驾驶行为的研究中已经有所体现[18].此因素对不受机动车影响下的越线超车影响最为显著. 同时本研究对不受参数影响下的生存概率进行了估算(速度按最低区间取值),利用MATLAB工具箱,采用指数函数拟合了不受以上两因素影响的基准生存概率,具体公式如下: S0(t2)=e-0.154t2 (26) 其中,拟合参数R2=0.723.则由式(21)及式(26),即可计算出车辆的越线自由行驶时间. 本研究将构建的上述系列模型应用于团队自主研发的微观仿真软件TESS NG,构建机非交互路段的非机动车越线超车模型,仿真流程如图3所示. 在仿真设置中,按照实际的数据设置机非交互路段环境.在路段属性中,选择设置长度为100 m的机非交互车道.软件中的非机动车(含电动车及自行车)及机动车流量输入均按周期的绿灯相位时长为单位输入,以保证车辆在一定时刻的到达密度,从而有效产生越线行为.非机动车的IDM跟驰模型及变道接受间隙模型按标定参数进行设置. TESS NG非机动车越线超车场景如图4所示.场景为非机动车已超越线内车辆,后受机动车影响正返回非机动车道. 3.3.1VISSIM机非交互路段环境设置 VISSIM是世界应用最为广泛的交通仿真软件,其在混合交通流仿真中也得到一定的应用.在VISSIM仿真软件中,可分别设置非机动车道和机动车道作为机非交互路段.非机动车辆在超车时可越过机非分隔线,进行机非交互路段的仿真.为与实际及TESS NG的场景保持一致,VISSIM仿真中非机动车道宽度同样设为2.4 m.非机动车及机动车道的驾驶行为设置为随意超车.软件中的机动车仅对期望速度进行设置. 图3 TESS NG仿真系统的非机动车越线超车流程 图4 TESS NG机非交互路段非机动车越线场景 3.3.2VISSIM的跟驰及变道模型标定 非机动车的跟驰模型同样按式(24)采用遗传算法进行标定,由于是城市道路,跟驰模型采用Wiedemann 74模型.需要标定的参数包括平均停车间距ax、安全距离的附加参数bx,add、安全距离的倍数影响bx,mult共3个参数,标定结果如表5所示. 表5 VISSIM非机动跟驰模型的参数标定结果 在VISSIM的变道模型中,主要对影响变道的最重要参数即最大协调减速度进行设置,此值为观测的统计均值,为-2.61 m·s-2. 3.3.3VISSIM非机动车典型越线超车场景 VISSIM软件中非机动车的越线超车场景如图5所示.在VISSIM仿真系统中,越线的非机动车辆会持续占用机动车道,即使在后方机动车影响下,也不会主动返回非机动车道. 图5 VISSIM中机非交互路段越线场景 本研究将实地采集的142组验证数据分别与仿真软件TESS NG、VISSIM的输出结果进行比较.比较指标包括越线超车次数、越线持续时间等微观指标,具体分析结果如下. 其中实测与仿真的越线超车非机动车数目,返回原车道非机动车道数目,持续占用机动车道的非机动车数目如表6所示. 表6 越线超车及返回原车道的非机动车数目 经仿真结果分析,TESS NG及VISSIM的越线超车数目均远小于实际的越线超车数目.主要原因包括:① 本研究侧重于对越线超车持续时间及间隙选择的比较,故本研究未对超车动机、超车时的横向距离等指标进行更细致的分析;② 在实际情况中,非机动车辆横向运行会具有更强的波动性,尤其在超车时,超车瞬间更倾向于与被超车车辆保持较大的横向间距(轻微越线即被计入越线超车).而仿真中车辆超车过程的横向位置相对固定,一部分实际越线的超车车辆在仿真中不会体现出越线效果. 在返回原车道的比例上,TESS NG与实测数据的比例更接近,百分比绝对误差为7.36%.而VISSIM的越线返回比例仅为2.77%,与实际数据差异巨大,其主要原因为VISSIM软件中,在机非交互车道,非机动车不会因后方机动车影响而返回原车道,也不会在超车后主动返回原非机动车道,仅会在超车后在受前方车辆阻滞影响下,才会主动返回非机动车道,而在路段上,此种情况出现的概率较小,故导致车辆返回原车道的比例极低. 由于足够的越线超车次数样本是进行模型构建及特征分析的关键,本研究同时对模型应用的场景进行了分析.通过对不同机动车、非机动车流量,异质非机动车流中电动车比例对越线超车的敏感性分析,结果表明:一般当非机动车流量高于1 000辆·h-1,机动车流量低于1 600 辆·h-1,并且电动车比例在0.3~0.9区间时,非机动车越线超车频次一般高于50次·h-1,此时模型具有较强的适用性. 通过统计实际数据与TESS NG、VISSIM的车辆越线持续时间并添加完全数据与删失数据标签,按照式(14)~(17)计算生存概率,对比如图6所示. 图6 非机动车越线总持续时间生存概率 在越线持续总时间的生存概率方面,具有以下特征:① 实际数据下降得较为平均,在每个区间均有分布,而TESS NG在3~10 s的区间下降得较为平均,VISSIM在6~11 s下降得较为平均,这是由于在实际数据中,如0~3 s,车辆有轻微的越线超车,即只在超越目标车辆的瞬间越线,存在分布与0~3 s持续时间的越线,而TESS NG及VISSIM仿真中,具有较为明确的横向位置划分,越线车辆往往在超越目标车辆前即已变道至越线位置,越线最短时间也需要3 s左右.② 在删失生存概率的起点位置,实测数据为14.8 s(生存概率为0.17),TESS NG为10 s(生存概率为0.35),VISSIM数据为11.2 s(生存概率为0.77);TESS NG在其删失终点的生存率绝对误差为0.18,远低于VISSIM的0.42.③ 在中位生存时间上,即生存概率为0.5的时刻,实测数据为7.8 s,TESS NG为7.6 s,误差仅为2.56%,而VISSIM由于无返回车辆,具有超车动机的非机动车辆进入路段前半段及开始越线,持续占用机动车道,其越线超车时间波动范围较小,70%以上均超过了11.2 s,中位生存时间误差为43.58%.④ 仿真模型的最大越线超车时间略小于实际数据的最大越线超车时间(14.8 s),这主要是由于车辆在自由行驶时会受到侧向机动车或其他因素影响,其自由状态下不一定会一直保持期望速度行驶,而仿真环境对侧向影响考虑较少,其仿真运行平均速度会略高于实际环境的平均期望速度. 通过分析非机动车在越线开始至超越目标车辆的时间,越线后自由行驶的时间,返回原车道的时间(含返回时执行加减速的时间),其各部分的平均持续时间对比如图7所示. 图7 非机动车越线超车不同过程持续时间 Fig.7 Duration of different process of cross-line overtaking behavior of non-motorized vehicles 从越线开始至超越目标车辆的时间上,实际的平均时长为2.04 s,TESS NG的平均持续时长为2.24 s,VISSIM的平均持续时长为1.83 s,相对误差百分比分别为9.80%和10.29%.从平均自由行驶时间上,实际时间为3.18 s,TESS NG数据为2.95 s(相对误差7.23%),VISSIM数据为6.67 s(相对误差为109%).其中返回原车道时间上,VISSIM仅有2例自由返回的数据,并且其返回原车道持续时间极短.TESS NG相比于VISSIM也可以更加精准地仿真出各部分的行程时间,其越线前、后的行程时间描述准确率为90.12%,远高于VISSIM的67.40%. 本文针对机非交互路段非机动车越线超车行为的研究缺陷,提出了基于生存分析的超车持续时间预测模型,完善了非机动车越线超车模型体系及实现框架,并将模型整合入自主研发的微观交通仿真系统TESS NG中.最后与实测数据及现有微观交通仿真VISSIM进行了对比.主要结论如下: (1) 实际调查数据表明,在机非交互路段,非机动车的越线超车发生较为频繁,并且超车后的越线时间为超车前越线时间的2.33倍,超越目标车辆前、后的越线时间表现出了较强的非对称性. (2) 在越线超车持续时间方面,TESS NG的仿真准确度为90.12%,高于VISSIM的67.40%. (3) 在越线超车的中位生存时间方面,TESS NG仿真误差仅为2.56%,优于VISSIM的43.58%. 笔者未来进一步的工作是考虑机非交互路段的安全性建模,提高仿真模型对代理安全性指标模拟的有效性.
1.3 车辆超越目标车辆前的驾驶行为模型

1.4 基于生存分析的超车行驶时间预测


1.5 其他模型
2 数据采集与模型标定
2.1 数据采集基本信息

2.2 非机动车越线超车的基本特征分析
2.3 模型观测参数

2.4 模型参数标定


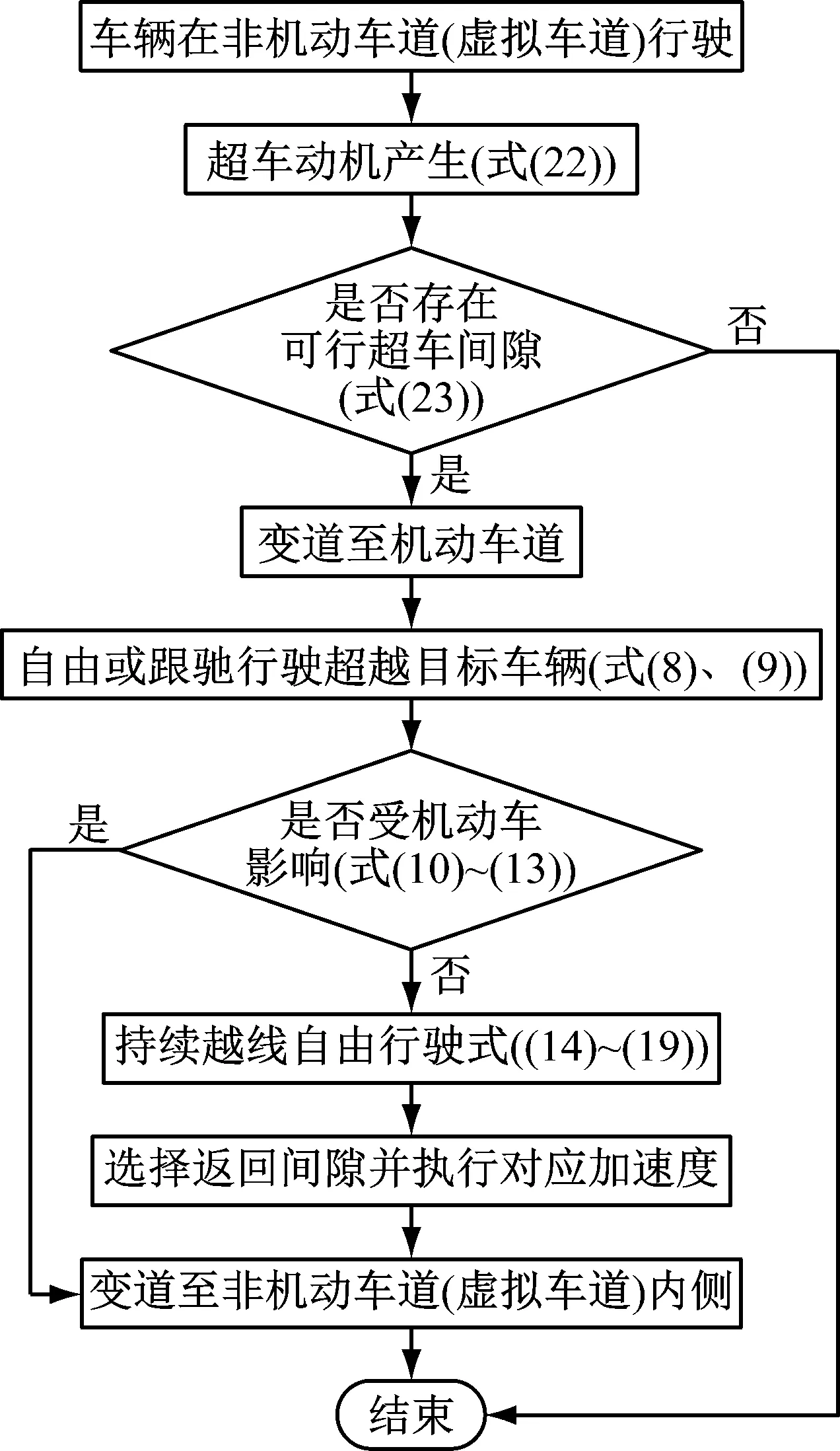
3 TESS NG仿真平台的系统构建与VISSIM仿真场景的搭建
3.1 TESS NG仿真平台搭建
3.2 TESS NG软件中机非交互环境设置
3.3 VISSIM仿真环境及参数设置


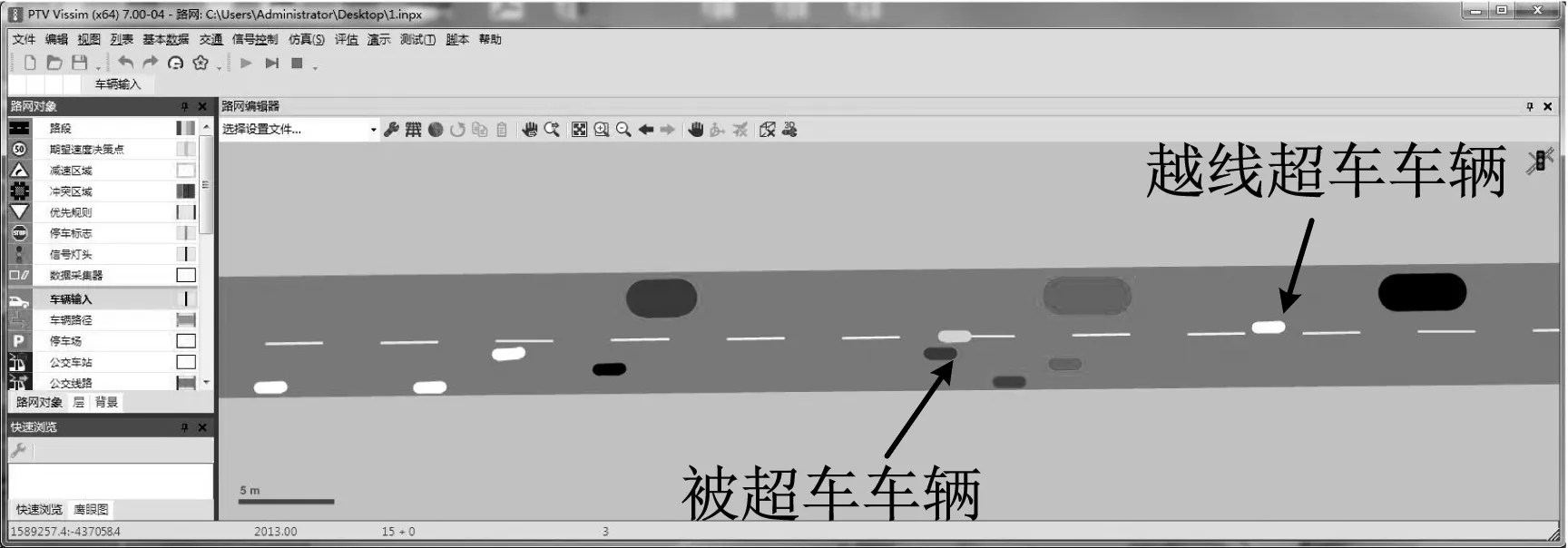
4 仿真结果分析
4.1 越线超车车辆及返回原车车辆数目

4.2 车辆的越线超车时间生存概率
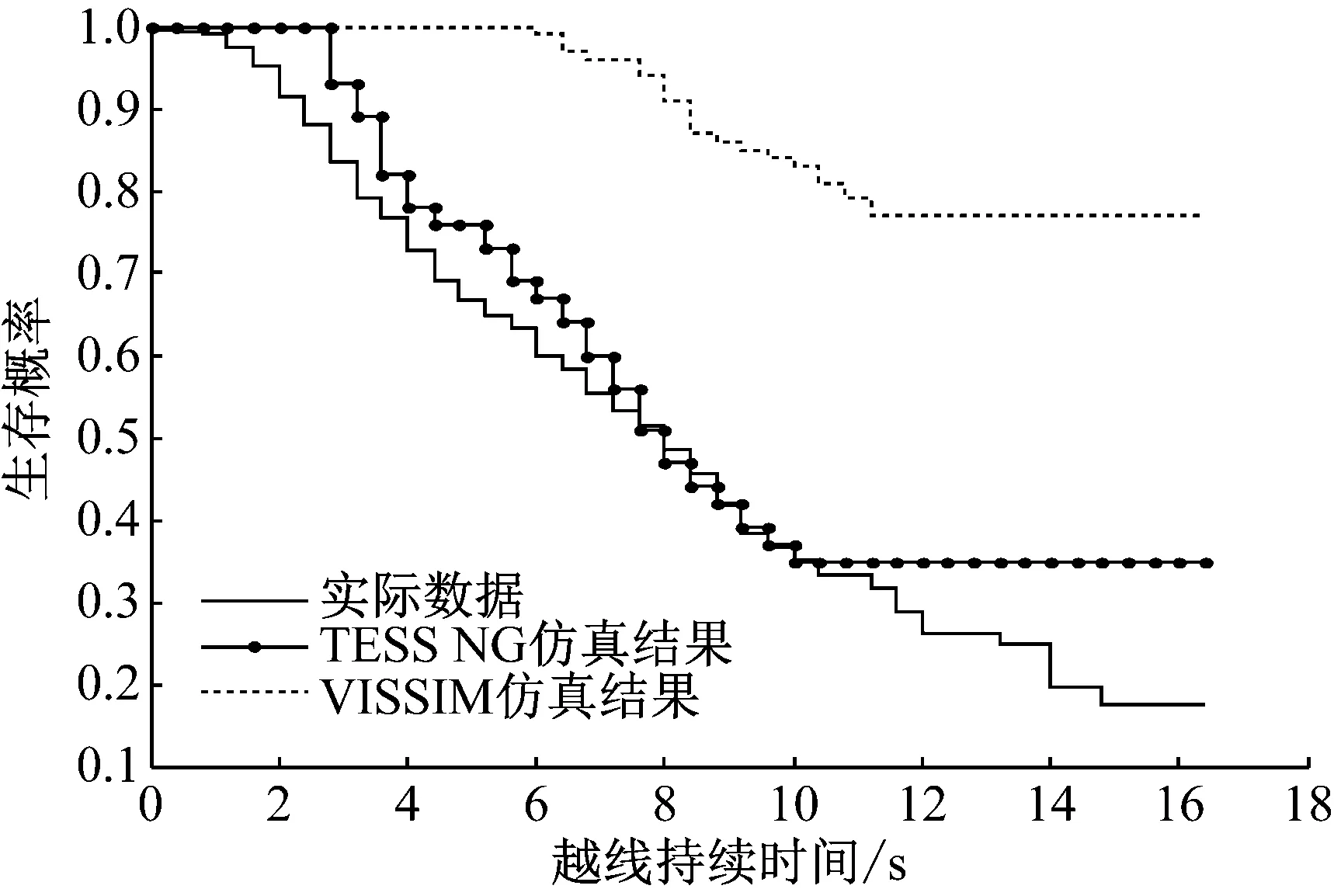
4.3 越线超车前、后的时间对比
5 结论
