考虑轨道几何不平顺的钢轨裂纹萌生与磨耗共存预测
2019-12-02黄旭炜王树国
周 宇, 黄旭炜, 王树国, 王 璞
(1. 同济大学 道路与交通工程教育部重点实验室, 上海 201804; 2. 同济大学 上海市轨道交通结构耐久与系统安全重点实验室, 上海 201804; 3. 中国铁道科学研究院集团有限公司 铁道建筑研究所, 北京 100081)
滚动接触疲劳裂纹萌生与磨耗发展同时存在,共同影响钢轨寿命[1].尽可能真实地考虑实际车辆-轨道作用、车轮-钢轨接触,从而预测疲劳裂纹萌生和磨耗共存是钢轨养护维修的关键.
Madge等[2]采用Archard磨耗模型和临界平面法裂纹萌生预测模型分析了钛合金Ti-6Al-4V疲劳裂纹萌生和磨耗过程.Leen等[3]根据临界平面法,研究航空发动机花键联轴器的微动疲劳和接触磨耗共存问题.Zhang等[4]对人工髋关节假肢之间的磨耗-疲劳裂纹相互影响进行了分析.可见疲劳裂纹萌生和磨耗共存的研究方法在其他金属领域有较好的探索.周宇等[5-8]提出考虑磨耗的钢轨疲劳裂纹萌生寿命预测方法,分析了钢轨硬度的影响,并在重载铁路、城市轨道交通等领域得到检验.但上述方法没有考虑轨道几何不平顺对轮轨接触关系的影响,当轮对横移量固定时车轮始终与钢轨在固定位置接触,与实际情况不符[9],因此,有必要在裂纹萌生和磨耗共存预测中考虑轨道几何不平顺的影响.
本文在钢轨裂纹萌生和磨耗发展共存预测方法的基础上,考虑轨道几何不平顺对轮轨接触位置的影响,以轮轨接触点在钢轨上的分布概率来改进磨耗和疲劳累积过程.
1 考虑几何不平顺的钢轨裂纹萌生和磨耗发展预测方法
1.1 裂纹萌生与磨耗发展共存预测方法
在裂纹萌生与磨耗发展共存预测方法中[5],将轮轨作用下疲劳裂纹萌生和磨耗同时存在、共同发展的连续过程,离散成有限个车轮作用引起材料疲劳累积、磨耗和钢轨型面变化,直至疲劳裂纹萌生的过程.如图1所示,裂纹萌生和磨耗共存发展的每一个离散阶段主要分成两个子阶段[10]:① 磨耗-疲劳单独发展子阶段,② 磨耗型面替换-疲劳累积子阶段.这两个子阶段的过渡是受钢轨磨耗到限、型面发生更替来控制的.在磨耗-疲劳单独发展子阶段,钢轨型面暂时保持不变,磨耗和疲劳损伤分别单独计算和累积.当磨耗量到达设定值时,进入磨耗型面替换-疲劳累积阶段,钢轨型面首先替换为本阶段磨耗后的型面,同时,累积车轮通过次数和轨头各点疲劳损伤.之后进入下一个离散阶段,这时的钢轨型面已经替换成了上一阶段得到的磨耗型面,轮轨接触和由此引起的应力应变、疲劳累积、磨耗位置和磨耗量相应都发生变化,如此循环直到钢轨任意点的疲劳累积损伤达到临界值,则认为该点萌生疲劳裂纹.可见在上述仿真过程中,轮轨接触是引起钢轨磨耗和疲劳损伤的前提,受到轨道几何不平顺的影响.
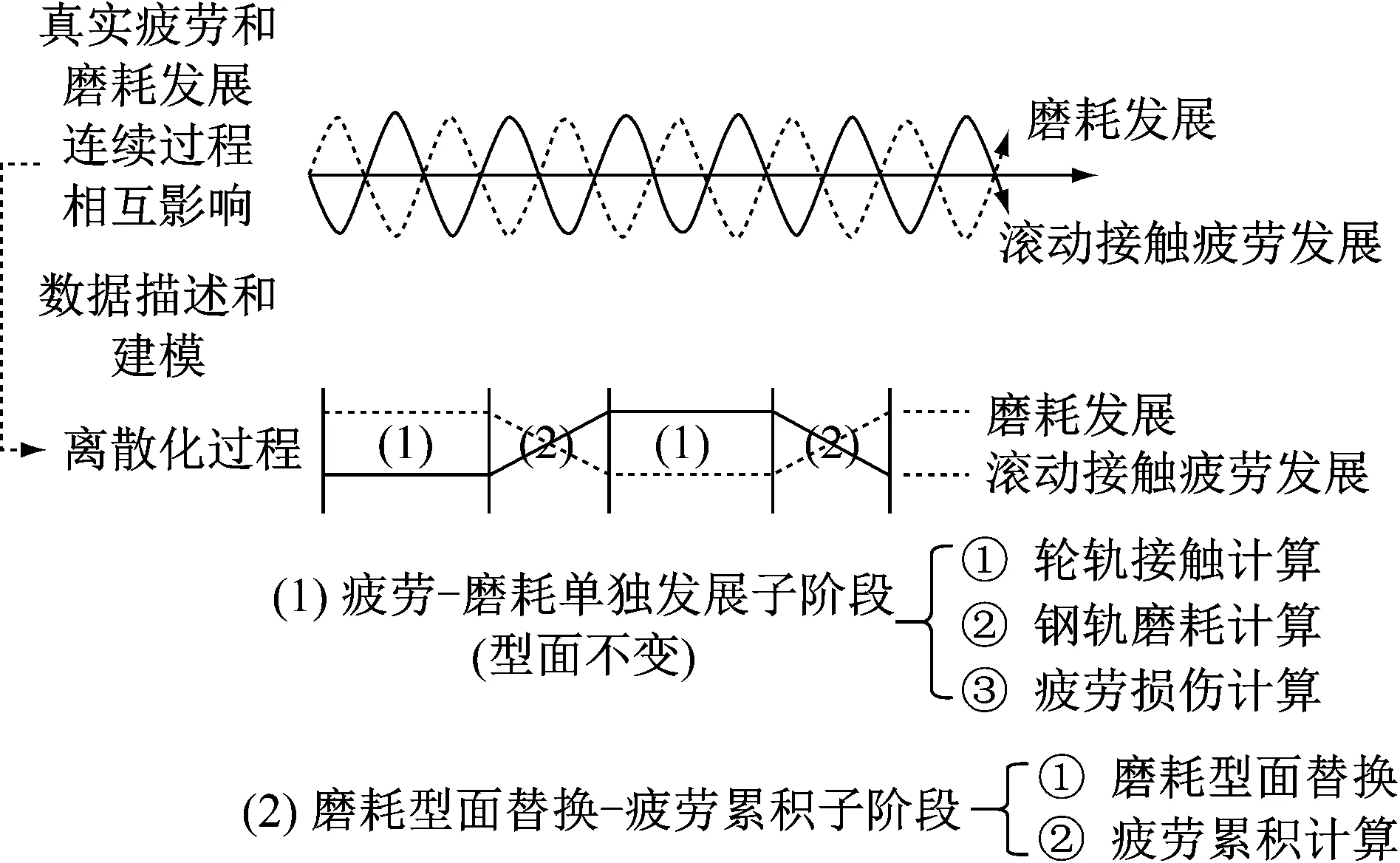
图1 裂纹萌生和磨耗发展共存预测思路
1.2 轨道几何不平顺引起的轮轨接触点变化
采用多体动力学软件Simpack,建立车辆-轨道动力学模型.以任意1节车第1轮位通过圆曲线为例,其中车轮型面为LM磨耗型,钢轨型面为75 kg·m-1标准型面,且不考虑轮轨磨耗,曲线半径800 m,轨道几何不平顺为实测的某重载铁路轨向不平顺.当该轮对前进时,其横移量变化如图2a所示,外轮外轨接触点位置随之变化的分布如图2b所示.图中,纵坐标正值为钢轨轨距边方向,横坐标正值为仿真中的时间发展.

a 第一轮对横移量

b 外轮在曲线外轨上的接触点位置分布
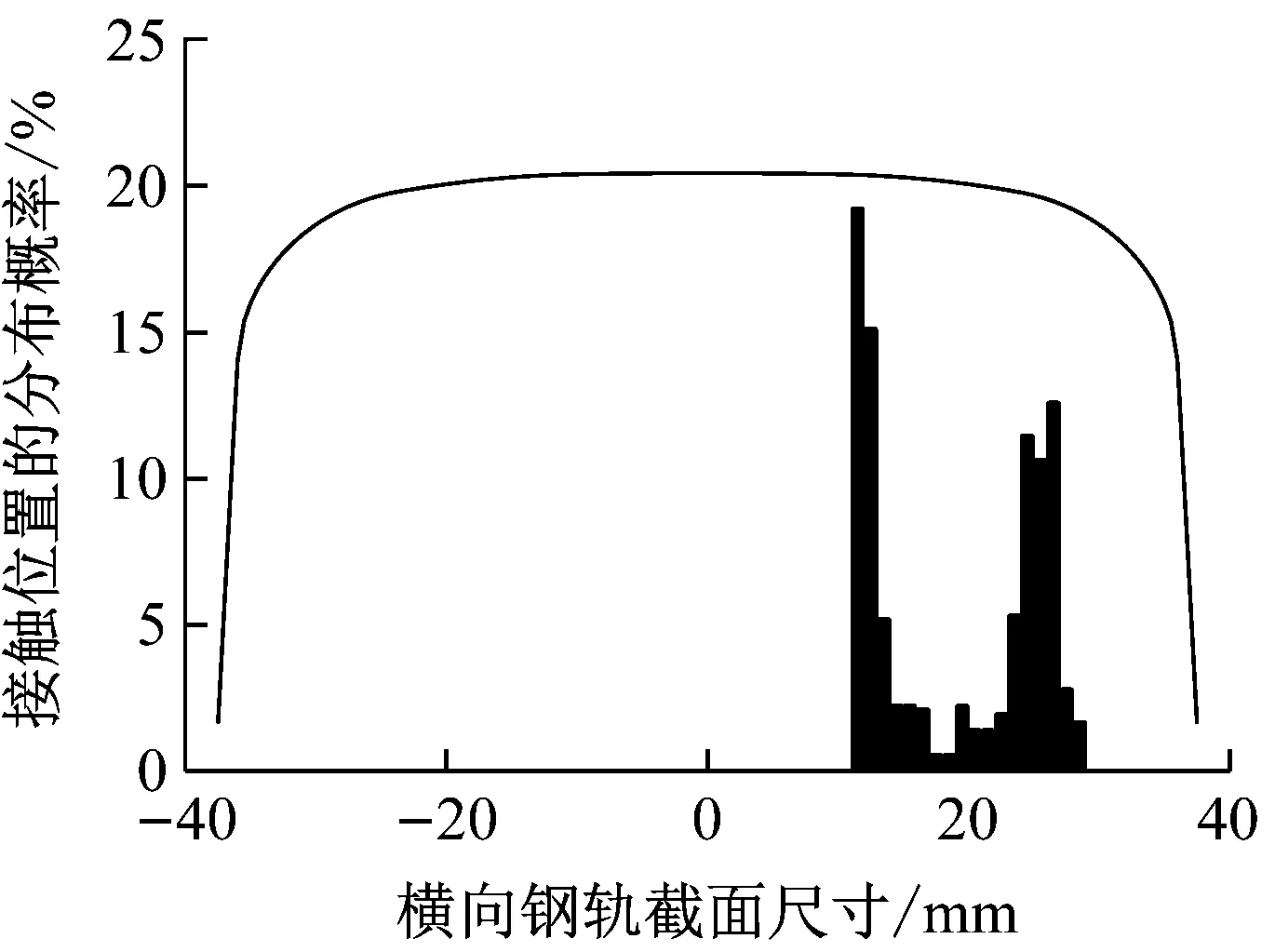
c 外轮在曲线中点外轨上的接触点分布
同理,若考虑一定数量的车轮通过曲线中点处的外轨横断面,轮轨接触点位置如图2c所示.可以看出,轮轨接触点因轨道几何不平顺在轨头呈一定范围的分布,且在分布范围内每一位置上的分布频率也不相同.这种情况可以由现场观测所证实,如图3所示,某重载铁路800 m半径曲线的外轨,新轨上道至通过总重约7~8万t期间,轮轨接触光带分布主要在轨肩-轨距角和轨顶中心.虽然现场钢轨光带分布情况还与不同型面的车轮接触有关,但可以发现轨道几何不平顺使得接触点在轨面一定范围内以不同的概率分布.

图3 现场观测的新轨接触光带情况
1.3 考虑轨道几何不平顺的钢轨磨耗计算
首先,采用前述车辆-轨道动力学模型计算考虑几何不平顺情况下轮轨接触点在钢轨横断面的接触位置分布及其轮轨力.然后,采用轮轨接触模型计算接触斑蠕滑状态和应力分布[7,11],再基于Archard磨耗理论[9]分别计算接触斑滑动区在钢轨横断面每个位置引起的磨耗量.最后,按接触斑在横断面各个位置的分布概率来累加磨耗量.
以1节车第1轮位的外轮通过曲线中点的钢轨横断面为例,将所有接触斑作用在钢轨横断面上的范围等分为n,记做n个接触位置,且每份宽度远小于1个轮轨接触斑的宽度,使得接触斑中心位于每个接触位置的中心.因为接触斑在相邻的接触位置时,分别引起的轨面磨耗会叠加,所以再将钢轨可能的磨耗范围等分成m,记做m个磨耗位置,如图4所示.
图4中,假设1个接触斑位于第1个接触位置时,其对钢轨横断面所有m个磨耗位置造成的磨耗深度为α1,该值为横断面各位置的磨耗深度合集,以矩阵形式表示为

图4 考虑轨道几何不平顺的钢轨磨耗计算
(1)
式中:Z11、Z12、…、Z1i、…、Z1m为1个接触斑位于第1个接触位置时在横断面1~m个磨耗位置处分别造成的磨耗深度.每个值是将接触斑沿钢轨纵向方向分成纵向条带,按其滑动区面积,根据Archard磨耗理论分别计算得到[5,7,12].同时从图4可以看出,接触斑未影响到的磨耗位置(如磨耗位置i+1~m)不会产生磨耗.因此,1个接触斑在第1~n个接触位置分别接触时,引起的钢轨横断面所有磨耗位置的磨耗深度可汇总为
(2)
再假设1个接触斑作用在钢轨每个接触位置中心的概率分别为β1、β2、…、βn,记做
(3)
若车轮通过次数为W,则在第n个接触位置上车轮的通过次数为Wβn,该接触位置引起的磨耗深度为Wβnαn.由此,钢轨横断面总磨耗深度αsum为
αsum=Wβ1α1+Wβ2α2+…+Wβiαi+
(4)
平均每次车轮通过造成的横断面磨耗量αavr为
(5)
可以看出,上述方法将考虑轨道几何不平顺后的轮轨接触斑根据其分布频率分散到了钢轨横断面不同的可能接触位置,对轨面某一位置的磨耗也做了量化划分和累积.
1.4 考虑轨道几何不平顺的钢轨疲劳损伤累积
临界平面法认为,当通过材料内部某点的任意平面上的应力应变引起的疲劳参量P为最大值时,疲劳裂纹在该点萌生[13].但考虑磨耗和疲劳裂纹萌生共存过程时,磨耗引起钢轨型面发展变化,使得轨头内任意点的疲劳损伤随型面发展变化呈阶段性累积.假设第R个型面被第R+1个型面替换前,共有fR次车轮通过,则第R个型面上第j点的量纲一的疲劳损伤DRj为
(6)
式中:FRj为第R个型面不发生磨耗时,其上第j点的裂纹萌生寿命(车轮通过次数).而实际上由于磨耗,第R个型面在车轮通过次数为fR时就达到磨耗规定值而被替换为下一个磨耗型面.
随着钢轨型面的磨耗变化,假如型面上的第j点没有在磨耗过程中被磨掉,根据Miner线性疲劳累积法则,当∑Dj=D1j+D2j+…+DRj=1时,认为在第R个型面的第j点上裂纹萌生,其磨耗和疲劳累积的过程如图5所示,轨头右侧统一为轨距边.图中,粗实线R1为预测开始时的初始钢轨型面,R2、R3、…、RR分别为按磨耗规定值(定义为型面任意点的最大垂直磨耗量=0.03 mm)依次形成的磨耗型面.图5中钢轨型面内的黑点为轨头内发生疲劳损伤累积的点,其中A点是疲劳累积最快、最后萌生裂纹的点,f1、f2、…、fR均为该型面在替换前的车轮通过次数.
当考虑轨道几何不平顺时,fR、FRj、DRj均随接触斑的位置发生变化.
以1节车第1轮位的外轮通过曲线中点的钢轨断面为例,第R个型面时轨头第j点的疲劳损伤为
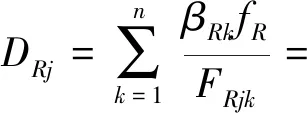
(7)
式中:βRk为第R个型面时1个接触斑作用在钢轨第k个接触位置的概率,由式(3)得到;FRjk为第R个型面不发生磨耗时,1个接触斑作用在钢轨第k个接触位置在j点的裂纹萌生寿命.

a 第1个磨耗型面对应的疲劳累积点
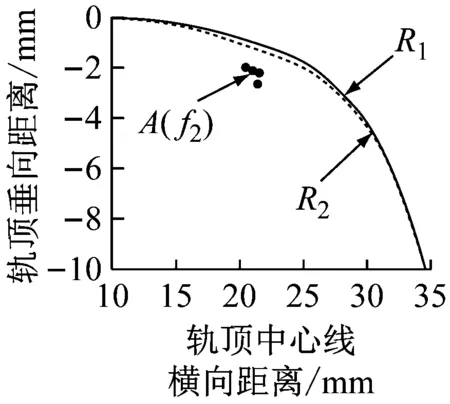
b 第2个磨耗型面对应的疲劳累积点
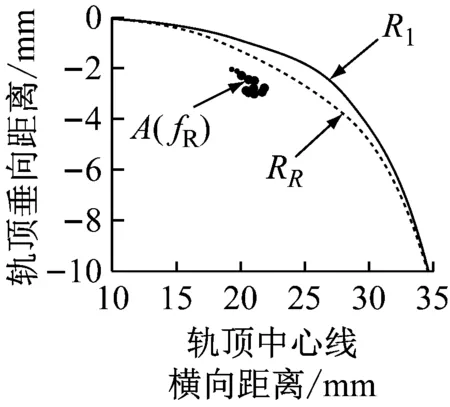
c 第R个磨耗型面对应的疲劳累积点
式(7)中任意一个接触位置的FRj可由下式计算:
(8)
(9)
式中:σ′、τ′分别为拉伸、剪切疲劳强度系数;ε′、γ′分别拉伸、剪切疲劳延性系数;b为疲劳强度指数;c为疲劳延性指数;PRj max为第R个型面时钢轨j点的疲劳参量最大值; 〈〉为MacCauley括号,〈σmax〉=0.5(|σmax|+σmax);σmax为裂纹面上的最大正应力;Δε为车轮与钢轨接触时引起的各点所有平面上的正应变幅值最大值;Δτ和Δγ分别为车轮与钢轨接触时引起的各点所有平面上剪应力幅值和剪应变幅值的最大值;J为材料参数.
1.5 预测流程
考虑几何不平顺的钢轨裂纹萌生和磨耗发展共存预测流程如图6所示.

图6 考虑几何不平顺的钢轨裂纹萌生和磨耗发展共存预测
根据上述计算方法,结合重载铁路曲线外轨表面疲劳裂纹的现场跟踪观测及其车辆-轨道条件[14],采用实测轨道几何不平顺,建立模型预测曲线中点外轨的疲劳裂纹萌生和磨耗共存发展.仿真参数见表1.
需要注明的是,轨道几何不平顺输入条件可以采用几何不平顺谱反推随机不平顺或者直接采用实测几何不平顺数据.这里采用实测高低和轨向不平顺数据.
2 仿真结果
2.1 钢轨磨耗
考虑到磨耗引起的型面变化,定义接触斑在轨面的接触位置和磨耗位置n=m=15~25逐渐变化.在保证计算精度的同时控制计算时间,再将接触斑在轨面的分布概率按其分布范围等分为3份,对单节车的4个外轮通过曲线外轨中点的轮轨接触情况进行统计,并计算该位置钢轨横断面磨耗.由于单节车前后转向架的导向轮(1位轮和3位轮)和从动轮(2位轮和4位轮)在几何不平顺影响下仅接触位置、接触状态不同,所以这里以第1、2轮位的外轮为例,第1个型面阶段(标准新轨型面)的轮轨接触点位置分布见图7,轨头右侧为轨距边.

表1 模型仿真参数
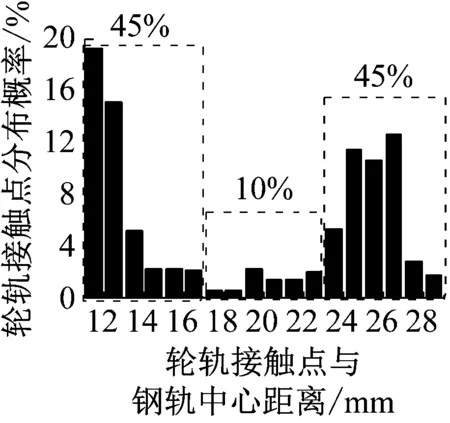

a 第1轮位外轮与外轨接触


b 第2轮位外轮与外轨接触
从图7可以看出,第1个型面阶段的第1轮位外轮与外轨的接触点分布在距轨顶中心11~29 mm的范围,将其接触范围等分3份,这3个接触位置的分布概率分别约为45%、10%和45%.同理,第2轮位的接触点分布在距轨顶中心11~27 mm的范围,3个接触位置上的分布概率约为50%、20%和30%.轮轨接触位置分布随着型面改变而变化,图8为第3个型面阶段的接触位置分布.


a 第1轮位外轮与外轨接触


b 第2轮位外轮与外轨接触
从图8可以看出,第3个型面替换阶段的第1轮位外轮与外轨的接触点分布范围扩展到距离轨顶中心10.5~30.5 mm,3个接触位置区域的分布概率分别为44%、23%和33%.第2轮位的接触点分布范围扩展到距离轨顶中心9~30 mm,3个接触位置区域分布概率分别为37%、25%和38%.
这样,统计每个型面阶段接触斑的分布概率,再按式(1)~(5)进行磨耗计算.
图9为考虑轨道几何不平顺情况下第3个型面阶段时,第1、2轮位外轮分别引起外轨在3个接触位置上的单次磨耗量.图10为考虑轨道几何不平顺情况下第1、2轮位外轮在3个接触位置引起的磨耗量的叠加,并与未考虑不平顺的结果对比.从图9和图10可以看出,考虑轨道几何不平顺后,轮轨接触点位置更加分散,形成的钢轨磨耗范围也更宽.
当预测发生裂纹萌生时,钢轨型面替换了6次,放大轨头磨耗位置,其型面变化如图11所示.
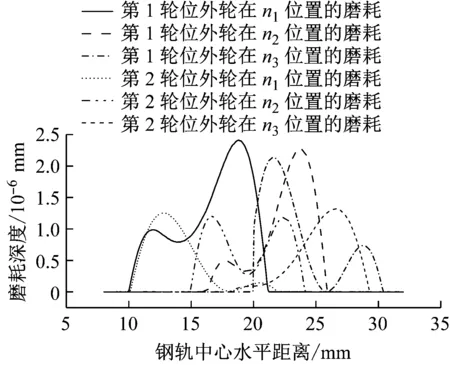
图9 不同接触位置的车轮引起单次磨耗深度

图10 第1、2轮位外轮引起的钢轨单次磨耗深度

图11 考虑轮轨接触位置分布时的钢轨型面变化
根据钢轨型面替换前后的磨耗量及对应的车轮通过次数,可以计算每个型面阶段的钢轨横断面磨耗发展率(1个磨耗阶段起、终时的两个钢轨横断面各点垂直磨耗量之和与该阶段车轮通过次数之比)和裂纹萌生时的平均磨耗发展率(各磨耗阶段磨耗发展率之和与磨耗阶段的数量之比).考虑和未考虑轨道几何不平顺情况下的各型面阶段磨耗发展率如表2所示.
从表2可以看出,与未考虑轨道几何不平顺的结果相比,考虑几何不平顺情况下每个型面替换时的阶段磨耗发展率和裂纹萌生时的平均磨耗发展率均较小,其中平均磨耗发展率降低约15.92%,同时,每个型面替换阶段的车轮通过次数较多.这是由于考虑轨道几何不平顺时,轮轨接触范围和磨耗范围均变宽,磨耗在轨头的分布较分散,因此车轮通过次数较多、磨耗发展率较低.
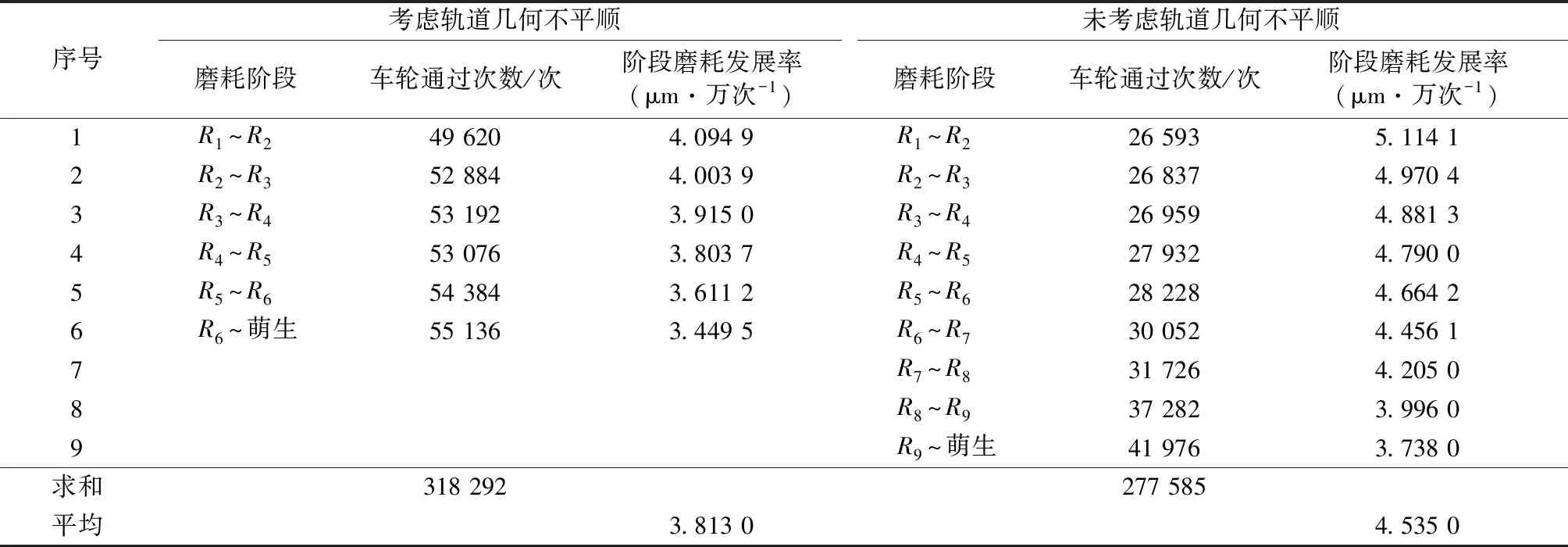
表2 考虑和未考虑轨道几何不平顺的钢轨磨耗发展率
2.2 钢轨疲劳损伤与裂纹萌生
考虑和未考虑轨道几何不平顺情况下的钢轨疲劳阶段损伤和累积损伤如表3所示,各阶段对应的车轮通过次数参见表2.

表3 考虑和未考虑轨道几何不平顺的钢轨疲劳损伤
从表3可以看出,随着钢轨型面磨耗发展,单次车轮循环对钢轨造成的损伤呈非线性增大的趋势[8].将两种方法的疲劳累积损伤发展和疲劳损伤分布进行对比,结果如图12、13所示.图13钢轨廓形中的小点为轨头进行疲劳累积计算的点.

图12 疲劳累积损伤发展对比
从表3和图12、13可以看出,考虑了轨道几何不平顺的情况下,钢轨内部材料点产生疲劳并持续累积的范围较大,裂纹萌生寿命约为318 292次,增大约14.66%.裂纹萌生位置与钢轨中心水平距离为17.66 mm,与钢轨顶面垂向距离为2.87 mm,较未考虑不平顺时略远离钢轨中心,如图14所示.
这是由于考虑轨道几何不平顺时,轮轨接触范围和疲劳损伤范围均变宽,每个型面替换阶段的疲劳损伤较大,但磨耗较慢,型面替换次数少,所以疲劳累积速度慢,相应的疲劳裂纹萌生寿命较长.
2.3 仿真结果对比与验证
根据其他同类仿真分析和现场观测,对本文仿真结果进行对比和验证.目前对金属中萌生疲劳裂纹时的尺寸有不同的界定:临界平面法认为裂纹萌生时的尺寸为50~500 μm.Brustow[15]认为裂纹在表面长度约2 mm或深度约0.5 mm时属于萌生.而涡流裂纹深度检测仪精度通常为0.1 mm,因此以裂纹深度0.1~0.5 mm为萌生尺寸,观测现场与本文仿真同等条件下的重载铁路曲线,外轨裂纹萌生寿命约为3.52×107~8.14×107t(百万吨通过总重)[16],换算成车轮通过次数约为1.53×105~3.54×105次.

a 未考虑几何不平顺

b 考虑几何不平顺
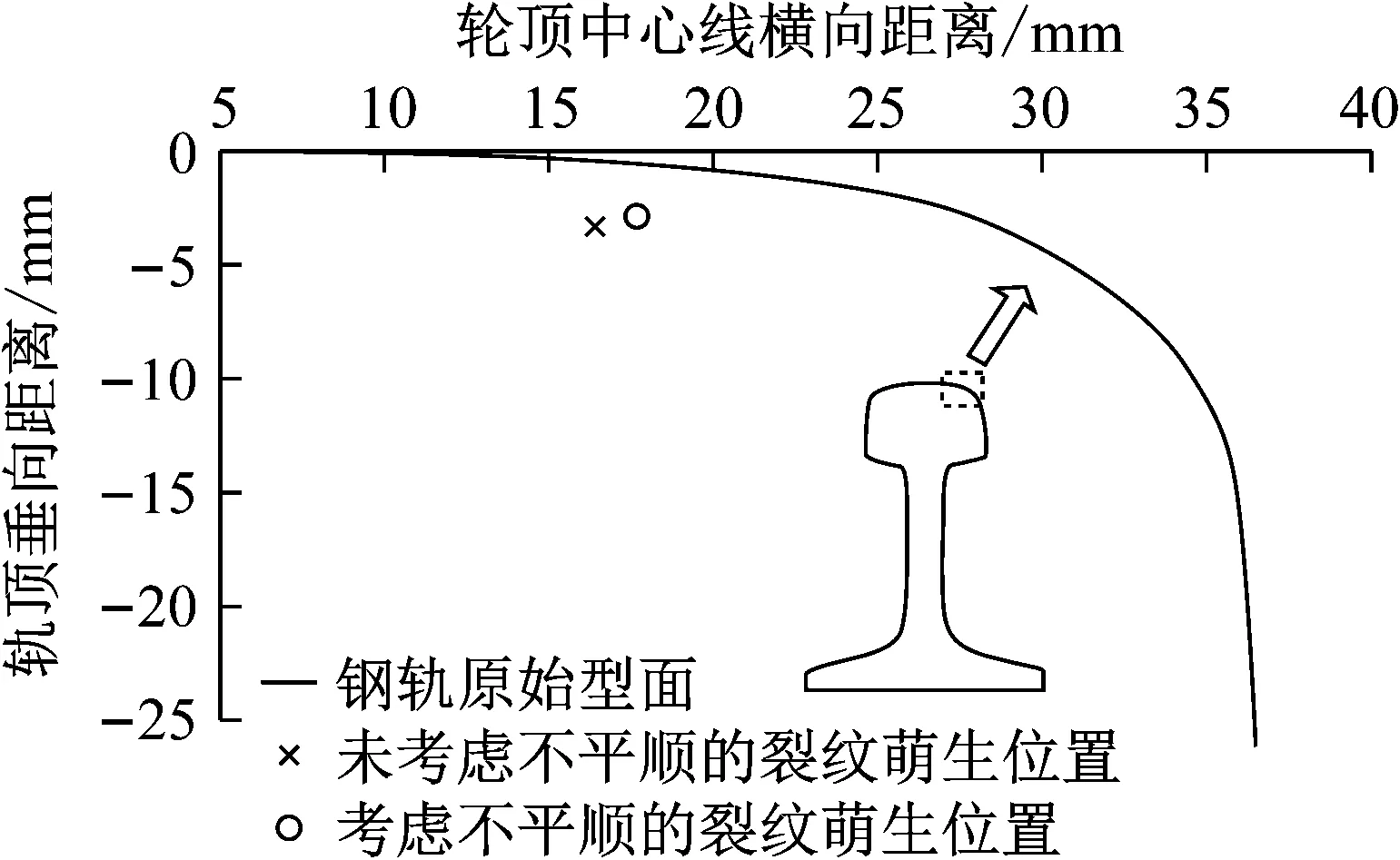
图14 钢轨裂纹萌生位置对比
此外,Makama等[17]采用临界平面法预测钢轨疲劳裂纹萌生寿命为车轮通过9.61×104~1.23×105次,同时现场观测的寿命为车轮通过5.10×104~6.07×105次;但上述仿真预测未考虑磨耗和轨道几何不平顺对轮轨接触状态、廓形变化和疲劳累积的影响,所以结果比本文预测小.
本文考虑轨道几何不平顺预测800 m半径曲线外轨的轨距角-轨肩疲劳裂纹萌生寿命为318 292次(约3.18×105次),在上述现场观测的裂纹萌生寿命范围内.同理,本文的方法也可以用于建立长编组车辆-轨道动力学模型,预测长编组列车作用下的钢轨表面疲劳和磨耗.
3 结论
(1) 在轨道几何不平顺的影响下,轮轨接触点的位置在轨面一定范围内以一定频率分布,且随着磨耗和型面变化,这个分布范围和分布频率均会变化,由此引起磨耗和疲劳损伤累积的变化.
(2) 考虑轨道几何不平顺后,钢轨磨耗形成更宽的磨耗范围,钢轨磨耗发展率相应减小.考虑轨道几何不平顺的曲线外轨钢轨的平均磨耗发展率为3.813 1 μm·万次-1,相较未考虑不平顺的结果降低了15.92%.
(3) 考虑轨道几何不平顺后,钢轨轨头内部应力影响范围以及疲劳损伤范围相应扩大,裂纹萌生寿命为318 292次,相较未考虑不平顺的预测结果增大了14.66%.裂纹萌生位置与钢轨中心水平距离为17.66 mm,与钢轨顶面垂向距离为2.87 mm.
