全国名校椭圆测试卷

■河南科技大学附属高级中学 陈广辉

一、选择题

1.已知△ABC的顶点B、C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )。

2.已知椭圆x2sinα-y2cosα=1 (0≤α＜2π)的焦点在y轴上,则α的取值范围是( )。

A.1 B.3 C.4 D.9

A.4 B.5 C.7 D.8

5.已知F1、F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A、B两点,若△ABF2是等边三角形,则这个椭圆的离心率是( )。

A.3 B.5

C.10 D.以上答案都不对

7.(2019年佛山一模)若椭圆mx2+ny2=1的离心率为,则=( )。

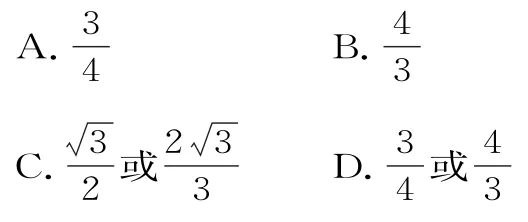
8.在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1、F2在x轴上,过F1的直线l交椭圆C于A,B两点,且△ABF2的周长为16,△AF1F2的最大面积为8,那么椭圆C的方程为( )。

9.在直角坐标系xOy中,F是椭圆C：=1(a＞b＞0)的左焦点,A、B分别左、右顶点,过点F作x轴的垂线交椭圆C于P,Q两点,连接PB交y轴于点E,连接AE交PQ于点M,若M是线段PF的中点,则椭圆C的离心率为( )。

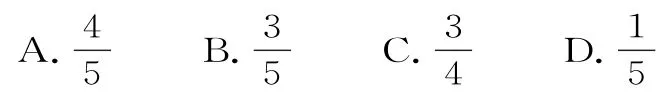
14.设F1,F2为椭圆的两个焦点,以F2为圆心作圆,已知圆F2经过椭圆的中心,且与椭圆相交于点M,若直线MF1恰与圆F2相切,则该椭圆的离心率为( )。

16.(2018 年昆明质检)已知F是椭圆=1(a＞b＞0)的左焦点,经过原点的直线l与椭圆交于P,Q两点,若|PF|=2|QF|,且∠PFQ=120°,则椭圆E的离心率为( )。

17.(2018年全国Ⅱ卷)已知F1、F2是椭圆=1(a＞b＞0)的左、右焦点,A是椭圆C的左顶点,点P在过A且斜率为的直线上,△PF1F2为等腰三角形,∠F1F2P=120°,则椭圆C的离心率为( )。

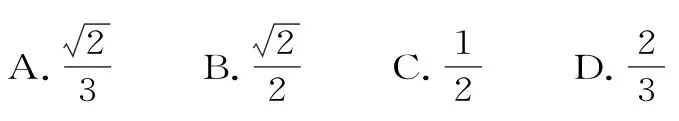
22.(2019年青海西宁复习检测)在平面直角坐标系xOy中,P是椭圆=1上的一个动点,点A(1,1),B(0,-1),则|PA|+|PB|的最大值为( )。

A.5 B.4 C.3 D.2

23.已知F1、F2分别为椭圆=1(a＞b＞0)的左、右焦点,过原点O且倾斜角为30°的直线l与椭圆C的一个交点为A,若AF1⊥AF2,=2,则椭圆C的方程为( )。

24.过原点的直线l与椭圆=1相交,若直线被椭圆截得的线段长不大于,则直线l倾斜角α的取值范围是( )。

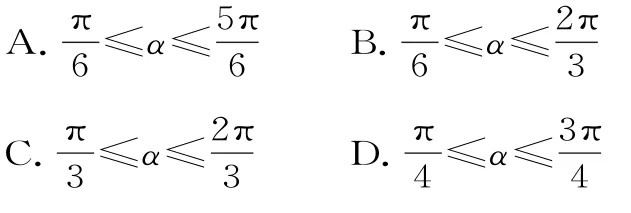
A.[-2,3] B.[-3,-2]

C.[-3,2] D.[2,3]

26.已知直线y=x-1 与椭圆交于AB两点,若以AB为直径的圆过左焦点F,则实数m的值是( )。

二、填空题

29.已知椭圆G的中心在坐标原点,长轴在x轴上,离心率为,且椭圆G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为_____。

32.椭圆C与椭圆的焦点相同,且与直线x-y+9=0有公共点,则椭圆C的短轴的取值范围是____。

33.(2019年浙江名校联盟)如果一个平面与一个圆柱的轴成α(0＜α＜90°)角,且该平面与圆柱的侧面相交,则它们的交线是一个椭圆。当α=30°时,椭圆的离心率是_____。

36.已知F1、F2是椭圆=1(a＞)的左、右焦点,在椭圆C上存在点P,使得△PF1F2的面积为4,△PF1F2的内切圆半径为,则椭圆C的离心率为____。

38.(2019年全国Ⅲ卷)设F1、F2为椭圆的两个焦点,M为椭圆C上一点且在第一象限。若△MF1F2为等腰三角形,则点M的坐标为____。

39.(2017年河北唐山统考)平行四边形ABCD内接于椭圆,直线AB的斜率k1=1,则直线AD的斜率k2=____。

40.(2019 年上海虹口一模)一个底面半径为2 的圆柱被与底面所成角是60°的平面所截,如图1,截面是一个椭圆,则该椭圆的焦距等于_____。

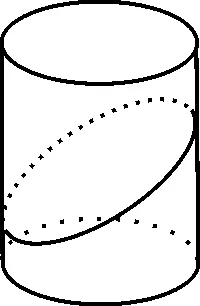
图1

43.已知点P是以F1、F2为焦点的椭圆=1(a＞b＞0)上一点,若PF1⊥PF2,tan∠PF1F2=,则此椭圆的离心率是____。

44.若点O和点F分别为椭圆+y2=1的中心和左焦点,点P为椭圆上的任意一点,则|OP|2+|PF|2的取值范围是_____。

46.圆x2+y2=r2(r＜3)的切线与椭圆=1 相交于A、B两点,O为坐标原点,若AO⊥BO,则r=____。

三、解答题

49.已知椭圆的中心在坐标原点O,经过点A(2,3),且点F(2,0)为其右焦点。

(1)求椭圆C的方程。

(2)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于4? 若存在,求出直线l的方程；若不存在,说明理由。

50.设F1、F2分别是椭圆(a＞b＞0)的左、右焦点,M是椭圆C上一点且MF2与x轴垂直,直线MF1与椭圆C的另一个交点为N。

(1)若直线MN的斜率为,求椭圆C的离心率；

(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b的值。

51.已知方向向量为v=(1)的直线l过点(0,-和椭圆=1(a＞b＞0)的右焦点,且椭圆的离心率为。

(1)求椭圆C的方程。

(2)若已知点D(3,0),点M、N是椭圆C上不重合的两点,且,求实数λ的取值范围。

52.(2018 年福建第二次质检)椭圆E：=1(a＞b＞0)的左、右焦点分别为F1、F2,离心率为,P为椭圆E的上顶点,△F1PF2的内切圆面积为。

(1)求椭圆E的方程；

(2)过F1的直线l1交E于点A、C,过F2的直线l2交椭圆E于点B、D,且l1⊥l2,求四边形ABCD面积的取值范围。

(1)求椭圆C的方程。

(2)过点M(0,1)的直线交椭圆于A、B两点,试问y轴上是否存在点N,使得直线NA与直线NB关于y轴对称。若存在,求出点N的坐标；若不存在,说明理由。

(1)求椭圆的方程。

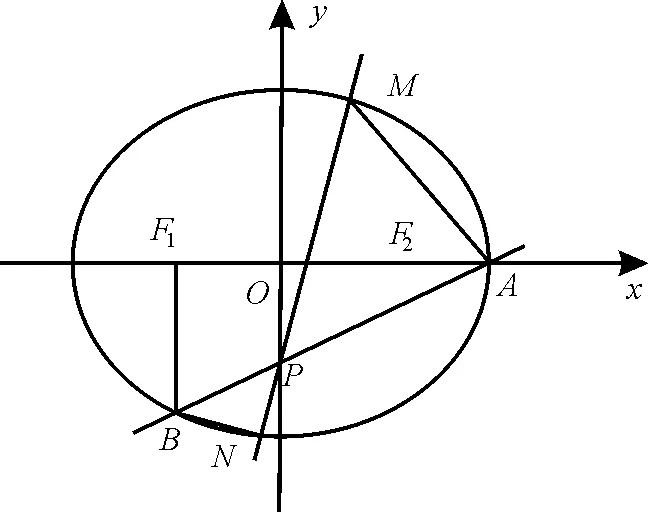
图2

(1)求椭圆C的标准方程。

(2)过点P且斜率大于的直线与椭圆交于M,N两点(|PM|＞|PN|),若S△PAM：S△PBN=λ,求实数λ的取值范围。

(1)求椭圆C的方程。

(2)设O为坐标原点,过点M(0,2)的动直线与椭圆C交于P、Q两 点,求的取值范围。

57.已知长为3的线段AB的两端点A、B分别在x轴和y轴上移动,且

(1)求点P的轨迹E的方程。

(2)过Q(0,1)作两条互相垂直的直线分别与轨迹E交于A,B和C,D,设AB中点为M,CD中点为N,试问：直线MN是否过定点? 若过,求出该定点；若不过,说明理由。

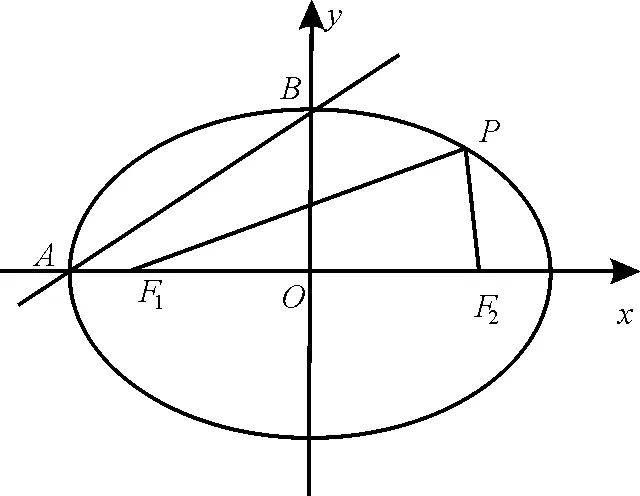
图3

(1)求椭圆E的方程。

(2)设C、D是椭圆E上不两同点,CD∥AB,直线CD与x轴、y轴分别交于M、N两点,且,求λ+μ的取值范围。