全国名校双曲线测试卷

■河南科技大学附属高级中学 李景荣

一、选择题

2.“ab＜0”是“方程ax2+by2=1表示双曲线”的( )。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

3.若双曲线8kx2-ky2=8 的一个焦点坐标是(3,0),则k=( )。

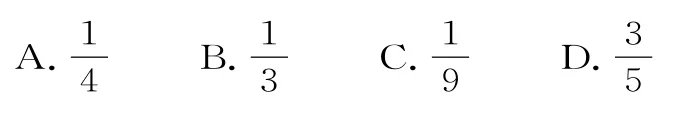
7.实轴长为2,虚轴长为4的双曲线的标准方程是( )。

8.两个正数a、b的等差中项是,一个等比中项是,且a＞b,则双曲线=1的离心率为( )。

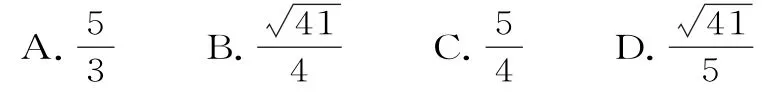
9.若双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m的值为( )。

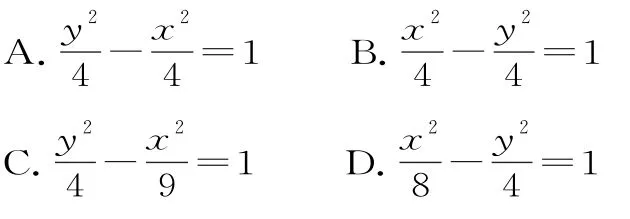
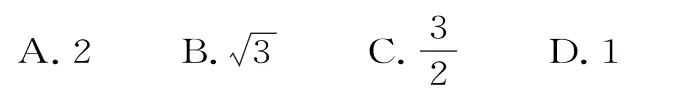
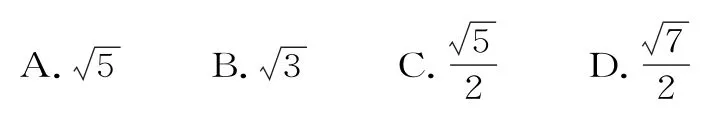
14.设△ABC是等腰三角形,∠ABC=120°,则以A,B为焦点且过点C的双曲线的离心率为( )。

15.已知0＜θ＜,则双曲线=1与=1的( )。

A.实轴长相等 B.虚轴长相等

C.离心率相等 D.焦距相等

16.双曲线x2-y2=1的顶点到其渐近线的距离等于( )。

A.24 B.36 C.48 D.96

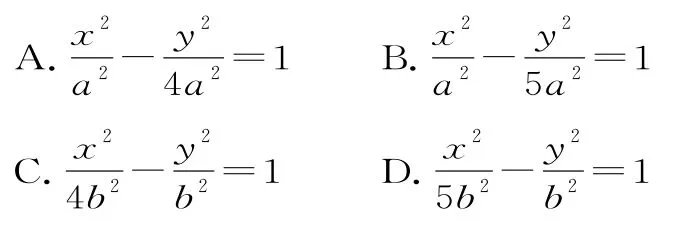
21.设F1、F2是双曲线=1 的左、右两个焦点,若双曲线右支上存在一点P,使PF1⊥PF2,且|PF1|=λ|PF2|,则λ的值为( )。

22.直线l：y=k(x-)与双曲线x2-y2=1 仅有一个公共点,则实数k的值为( )。

A.1 B.-1

C.1或-1 D.1或-1或0

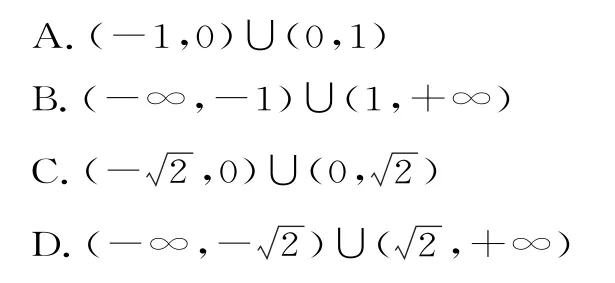
二、填空题

28.焦点在x轴上的双曲线经过点P(4,-3),且Q(0,5)与两焦点的连线互相垂直,则此双曲线的标准方程为_____。

29.已知双曲线x2-y2=1,点F1、F2为其两个焦点,点P为双曲线上一点,若PF1⊥PF2,则|PF1|+|PF2|的值为____。

32.双曲线x2-y2=1的右支上到直线y=x的距离为的点的坐标是____。

33.已知P是双曲线=1右支上的一点,双曲线的一条渐近线方程为3x-y=0。设F1、F2分别为双曲线的左、右焦点。若|PF2|=3,则|PF1|=____。

34.在平面直角坐标系xOy中,P为双曲线x2-y2=1右支上的一个动点。若点P到直线x-y+1=0的距离大于c恒成立,则是实数c的最大值为____。

三、解答题

36.已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为,且过点(4,-)。

(1)求双曲线的方程。

(2)若点M(3,m)在双曲线上,求证：点M在以F1F2为直径的圆上。

(1)求双曲线C的方程。

(2)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点M、N,若△OMN的面积为,求直线l的方程。

38.已知双曲线C∶-y2=1,P是C上的任意一点。

(1)求证：点P到双曲线C的两条渐近线的距离的乘积是一个常数。

(2)设点A的坐标为(3,0),求|PA|的最小值。

39.双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点。已知成等差数列,且与同向。

(1)求双曲线的离心率。

(2)设线段AB的长为4,求双曲线的方程。

(1)求双曲线C的渐近线方程。

(2)已知点M的坐标为(0,1),设P是双曲线C上的点,Q是点P关于原点的对称点,记,求λ的取值范围。

(3)已知点D,E,M的坐标分别为(-2,-1),(2,-1),(0,1),P为双曲线C上在第一象限内的点。记l为经过原点与点P的直线,s为△DEM截直线l所得线段的长,试将s表示为直线的斜率k的函数。

41.已知中心在原点的双曲线C的一个焦点是F1(-3,0),一条渐近线的方程是5x-2y=0。

(1)求双曲线C的方程。

(2)若以k(k≠0)为斜率的直线l与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为,求k的取值范围。