不同风速下Neil Pryde RS：X级别帆板帆翼空气动力性能单/双向流固耦合对比

雷晓珊 ，马 勇 *，蔺世杰

LEI Xiaoshan1，2，MAYong1，2*，LIN Shijie1，2

Neil Pryde RS：X（NP）级别帆板在2008年时正式成为夏季奥林匹克运动会比赛项目，其主要动力来源于风作用在帆翼上的空气动力，帆翼空气动力的大小直接影响比赛成绩（罗晓川，2010）。帆翼空气动力学研究的方法有理论分析、实验研究和数值计算。目前为止，传统的计算流体动力学（computational fluid dynamics，CFD）仿真方法通常将帆翼视为刚体，只考虑气流对帆翼气动性能的影响，很少考虑帆翼的变形以及相应的流固耦合问题，忽略了帆翼结构变形和振动与气流之间的耦合作用，进而导致在气动特性和结构方面的计算结果与帆翼实际状况存在一定的偏差（Augier，2012；Viola，2011；Persson et al.，2016）。在奥运会帆船帆板比赛时，常用航线为奥林匹克航线（蔺世杰等，2017），比赛中随着风速的变化，帆翼的结构形状变化较大，甚至产生振动，流固耦合效应更加显著，直接影响到帆板高速航行时帆翼空气动力性能（Bak et al.，2013；Durand et al.，2014）。

许多学者在运动帆翼的空气动力性能方面做了大量研究。王树杰等（2009）、何海峰（2012）利用数值模拟方法，研究了奥运级别NP帆板帆翼分别在稳态和瞬态下空气动力性能，分析讨论了不同状态下转角和频率的变化对帆翼空气动力性能的影响。Durand等（2014）基于非线性有限元方法进行耦合，对IMOCA60帆翼顺风航行时的空气动力性能进行了研究，考虑了帆翼褶皱、振动等问题，为帆翼的推进性和稳定性优化设计打下了基础。马勇等（2012，2013a，2013b，2013c，2016）基于风洞试验与CFD方法，对奥运会帆船帆翼的空气动力学特性进行研究，讨论了不同参数对帆翼空气动力性能的影响，得到了不同航向角下帆翼的升阻力、侧向力和横倾力矩等特性与帆翼攻角变化的关系。Sacher等（2017）利用ISIS-CFD与ARA耦合，对IMOCA主帆进行流固耦合计算，发现帆翼的气动力特性与试验结果较吻合。Deparday等（2018）对风角为50°～140°下的三角帆帆翼进行流固耦合研究，分析了帆翼的压力，发现来流帆缘气动弹性相对较弱且非稳定性振动发生在前帆。目前，基于流固耦合方法对帆翼空气动力性能的研究较多关注大三角帆，而小帆船帆翼研究主要集中在通过传统CFD方法进行空气动力性能研究，奥运会帆船帆板等帆翼流固耦合问题有待进一步研究。

本文以奥运女子级别的NP帆板帆翼为研究对象，基于ANSYS Workbench平台，采用单/双向流固耦合方法，对不同风速下帆翼进行三维数值模拟，对比双向流固耦合与单向流固耦合仿真计算结果在气动力、流场和结构等方面的差异，探讨单/双向流固耦合仿真方法的差异性，并揭示流固耦合效应对帆翼气动性能的影响。

1 研究方法

1.1 流体动力学数值求解

流固耦合计算中，由流体动力学求解提供了帆翼表面的气动载荷，在欧拉坐标系中，根据三大守恒定律，可得到流体控制方程：

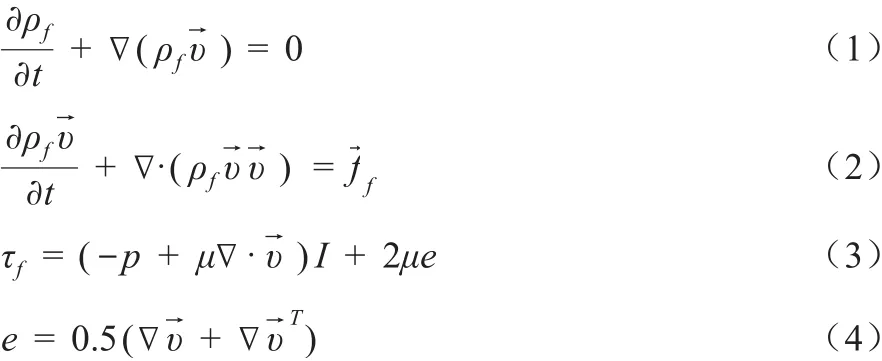
式中：t为时间；ρf为流体的密度→为速度矢量为流体介质的体积力矢量；τf为剪切应力张量；p为流体的压力；μ为动力粘度；e为速度应力张量。

1.2 固体模型的有限元分析

帆翼结构的动力响应可以用下面的运动方程描述：

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；F为由流体导致的作用在结构上的外力；u̇，ü分别为速度和加速度。

1.3 流固耦合交界面的动力学条件

根据已知的边界条件，通过逆解法和半逆解法进行求解，得到应变、应力和位移的结果数据。应力边界条件：

式中：n为单位法向量分量；τf为流体应力；τs为结构应力。

位移边界条件：

式中：df为流体位移；ds为固体位移。

2 数值模拟的建立

2.1 计算模型与网格

本文以奥运会女子级别的NP帆板帆翼为研究对象，实际航行如图1（A），计算速度为2～12 m·s-1，涵盖比赛过程中最常用的风速。帆翼主要规格参数如表1，通过对NP帆翼外形的测绘得到（罗晓川，2010）。基于ANSYS Workbench平台，采用单、双流固耦合方法对奥运女子级别的NP帆板帆翼进行迭代计算，在建模软件Design Modeler进行帆翼模型和流动区域的构建，得到三维模型。考虑到计算量、流场充分发展和模拟的真实性（马勇等，2012；Ma et al.，2016），确定采用以帆翼底边弦长为基准向前、左右和上各延伸6倍，向后延伸10倍的长方体为计算区域，帆翼和计算域位置设置如图1（B）。

帆板运动处于近海平面且空气流动速度不高，该流场可被视为不可压缩流体。通过对比不同湍流模型的优缺点，采用Realizable k-ε模型来计算湍流度（马勇等，2013a），在近壁面区使用壁面函数法进行处理。入口边界条件采用速度入口，入口速度按照工况要求而设定。出口条件采用自由流出，出口处速度满足流动充分发展。

图1 （A）实帆图（B）NP帆翼模型图Figure 1. （A）ASail Wing（B）Model ofASail Wing for NPClass

表1 女子NP帆板帆翼主要规格Table 1 Main Parameters of the Sail Wing for Neil Pryde RS：X Class

考虑流固耦合计算耗时较多，在保证足够计算精度的基础上，应充分发挥有限的硬件条件。本文进行了网格无关性验证，通过改变帆翼表面网格尺寸和帆翼表面第1层网格高度来改变网格数量，在不同网格数下对帆翼模型采用相同的算法进行模拟。由图2不同网格方案下升力、阻力系数对比可看出，当网格单元数大于209万时，网格单元数对升阻力系数影响极小。考虑到计算能力，同时兼顾计算精度，本研究选择第2种方案进行划分，整个流体域的网格单元总数为209万个。

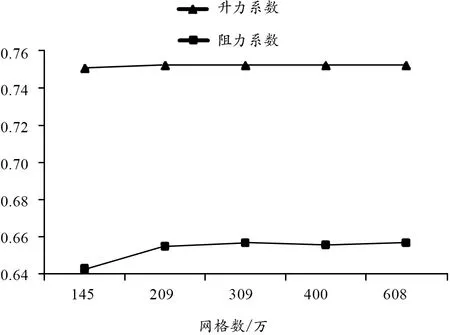
图2 不同网格方案下升力系数、阻力系数对比Figure 2.Comparison of Lift Coefficient and Drag Coefficient for Different Mesh schemes

2.2 计算方法与条件设置

在实际航行过程中，在不同风速下伴随着帆翼表面发生变形、摇摆等复杂的运动，需要采用动网格模型来解决这一问题（郭泽宇等，2018）。而帆翼由桅杆和帆面成拱形结构，且受风影响沿一个方向形变，属于小变形叠加状态，可通过弹簧光顺（霍世慧等，2011）和局部网格重构（庞宇飞等，2017）2种动网格方法混合，能够高精度和高效率地实现帆翼流固耦合过程。

帆面和桅杆使用高分子和碳纤维复合材料制造，材料属性在ANSYS自带的材料属性数据库中不存在，因此对实际比赛中的NP帆翼进行了相关的应力松弛实验，确定了各个材料的参数。为了简化计算的结构模型，假定NP帆翼模型帆面为各项同性材料，帆翼参数是：帆面弹性模量为 14.4 GPa、泊松比为 0.33、密度为 100.86 kg·m-3；桅杆弹性模量为161.7 GPa、泊松比为0.23。

3 结果与讨论

3.1 升力和阻力以及压力场分析

单/双向流固耦合效应的2种数值仿真方法，在求解得到的升力系数、阻力系数以及单/双向流固耦合时差异如图3。单/双向流固耦合数值计算得到的NP帆翼升力系数和阻力系数随着风速的改变而变化的趋势一致，都随着风速的增加而降低，且在风速为2 m·s-1时升、阻力系数都是最大。而双向流固耦合计算下，升、阻力系数变化过渡更圆滑，更接近实际情况。从气动力数据的结果对比发现，2种仿真方法的差异率都在9%以内，但是在风速为4 m·s-1时升力系数和阻力系数差异比其他风速时都要大，说明单/双向耦合对帆翼空气动力性能有不同程度的影响，而帆翼空气动力的大小直接影响到帆板的推进性能，关系到帆翼行驶的操纵稳定性。而考虑流固耦合效应的仿真方法更加贴切运动实际，有利于帆板操纵性的准确控制。

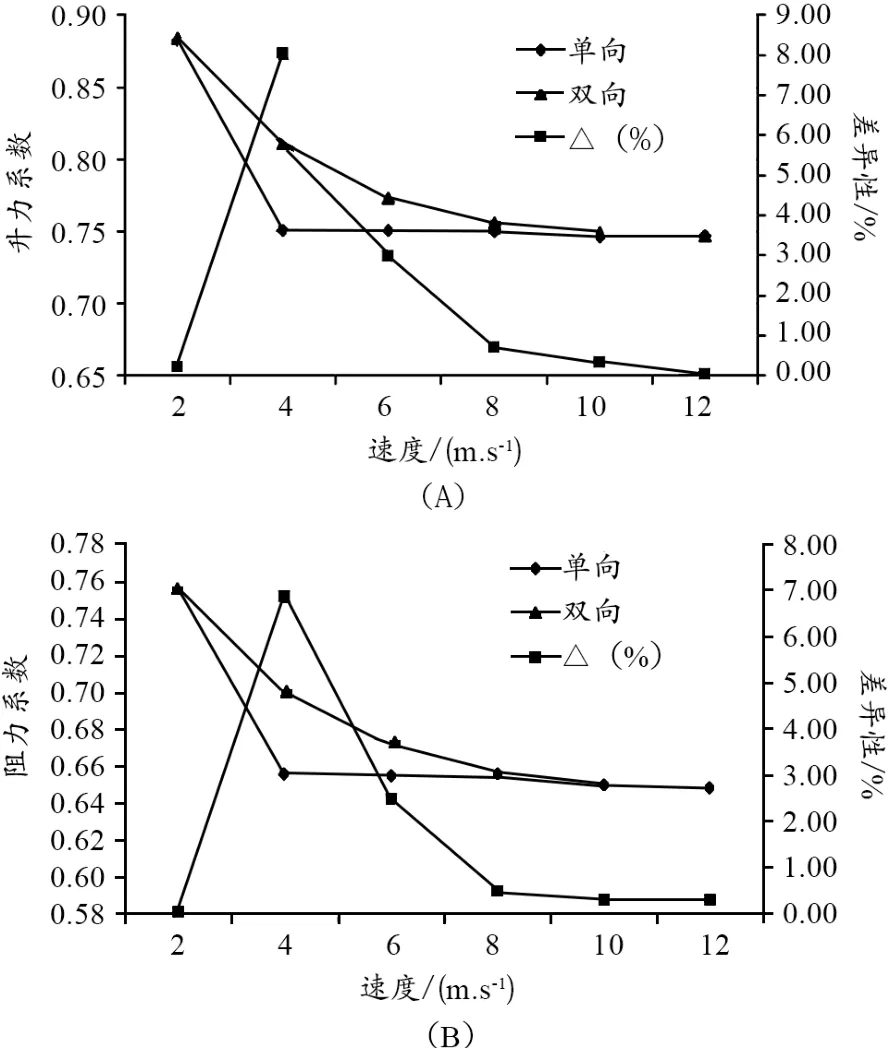
图3 单/双向流固耦合时（A）升力系数（B）阻力系数差异对比Figure 3.Comparison of（A）Lift Coefficient and（B）Drag Coefficient in One-way/Two-way Fluid-Structure Coupling

帆翼空气动力的产生，主要是由于帆翼前后表面存在压力差，本文进一步对比了6种风况下压力场的差异。通过对比2种仿真方法帆翼表面的压力数据发现，帆翼迎风面和背风面的压力都有一定差异。图4对比了流速从2～12 m·s-1仿真计算收敛后的2种耦合方式下Z=1.6 m横截面处流场压力的分布情况。对比显示，由于双向流固耦合效应作用下帆翼面发生变形，帆翼后方负压区增大。

图4 不同风速作用下Z=1.6 m截面处流场压力分布对比Figure 4. Comparison of Pressure Distribution of Flow Field at Z=1.6 m Section at Different Speeds

随着气流沿着帆翼表面流动，在背风面后部会逐渐脱落，当风速较高时会在背风面产生明显的涡脱现象，帆翼表面持续受到周期性的载荷作用而发生变形和振动，产生风激振现象，也会使帆翼周围流场发生变化。因此，考虑帆翼与流场的耦合效应十分有必要。

3.2 单/双向耦合时应变分析

6种风况下，帆翼的等效应变云图如图5，帆翼最大应变处都在桅杆上部附近和尾缘中部到下部，且其在气动力的作用下极易发生变形。随着风速的增大，帆面最大应变量变大，最大应变范围也相应地扩大。以风速12 m·s-1为例，采用单/双向流固耦合计算方法，帆翼最大变形量分别为4.65和7.95 mm，皆小于弦长的1%，即23.3 mm，在其允许的最大变形量内，符合帆翼设计的变形要求（图6）。

图5 不同风速下帆翼的等效应变云图Figure 5. Equivalent Strain Cloud Diagram of Sail Wing at Different Wind Speeds

由于气动力的作用，帆翼在经过一段时间的大幅度波动后，在2.0 s后逐渐平稳。表2为基于单/双向流固耦合计算的帆翼等效应变量的对比表，Do、Dt分别为单、双向流固耦合条件下的帆翼等效应变量。

3.3 单/双向耦合时应力分析

基于不同流固耦合方法计算时，帆翼应变分布图略有差异，但在不同风况下，帆翼最大应力都位于桅杆附近上部和尾缘下方区域。以风速12 m·s-1为例，采用单/双向流固耦合计算方法，帆翼最大应力值分别为4.109和7.237 MPa（图7）。表3为基于单/双向流固耦合计算的帆翼等效应变量和等效应力大小的对比表，σo、σt分别为单、双向流固耦合条件下的帆翼等效应力值。

图6 风速12 m·s-1时（A）单向耦合（B）双向耦合时帆翼的变形图Figure 6. Deformation Diagram of the Sail Wing under（A）Oneway Fluid-Structure and（B）Two-way Fluid-Structure Interaction at 12 m·s-1

表2 单/双向流固耦合计算的帆翼应变量比较Table 2 Comparison of the Strains of the Sail Wing under Oneway and Two-way Fluid-Structure Interaction

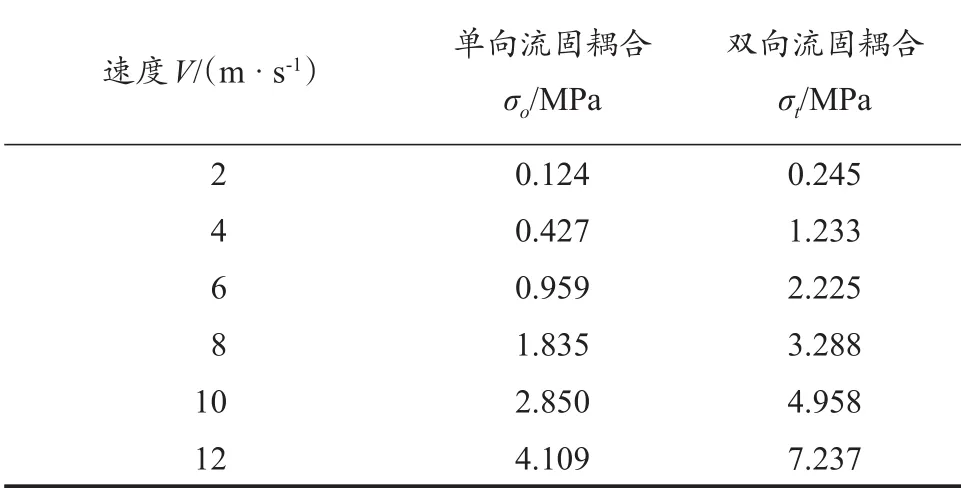
表3 单/双向流固耦合计算的帆翼应力大小比较Table 3 Comparison of the Stress of the Sail Wing under Oneway and Two-way Fluid-Structure Interaction

通过对比基于单/双向流固耦合方法的结构特性计算结果可以发现，相同工况下，双向流固耦合计算得到的帆翼的应力值略大，随着风速增加，两者的差值逐渐变大。结合图6帆翼变形云图可发现，双向流固耦合数值计算得到的应变更符合帆翼实际的变形情况。考虑到双向流固耦合计算时固体结构与流体之间的相互作用，及基于双向流固耦合方法下帆翼的变形量与应力值比单向流固耦合计算时过渡的更圆滑，从结构强度校核角度考虑，使用双向流固耦合的计算结果更保守、更接近实际情况。

图7 风速12 m·s-1时帆（A）单向耦合（B）双向耦合翼的应力云图Figure 7. Stress Diagram of the Sail Wing under（A）One-way Fluid-Structure and（B）Two-way Fuid-Structure Interaction at 12 m·s-1

4 结论

流固耦合效应对帆翼的升力和阻力产生不同程度的影响，考虑流固耦合效应的仿真方法对帆翼空气动力预测更加准确，有利于帆板操纵性的准确控制；单/双向耦合下帆翼最大应变处都在桅杆上部附近和尾缘中部到下部，在气动力的作用下极易发生变形；双向流固耦合计算得到的帆翼的应力值略大，随着风速增加，两者的差值逐渐变大。结合帆翼变形云图分析，双向流固耦合数值计算得到的应变更符合帆翼实际的变形情况。因此，研究帆翼空气动力性能时，流固耦合效应不可忽略，研究结果为运动员在训练和实际比赛中科学调整帆翼提供依据。