我国体育世界冠军获得情况的影响因素分析

2019-11-27李欣然

当代体育科技 2019年27期

李欣然

摘要：中国体育世界冠军获得情况受多种因素影响，本文主要利用线性回归分析法，研究中国获体育世界冠军的主要影响因素。首先，从外部和内部两大方面定性分析了世界冠军获得情况的影响因素，初步选取国际级运动健将人数等7个主要因素作为自变量，选取我国每年体育世界冠军人数作为响应变量。其次，通过对该经典模型的检验，发现模型可能存在多重共线性和异方差性，分别采用对数线性变换+逐步回归法、加权最小二乘法对模型进行修正，得到最终的预测方程。最后，对我国体育事业的发展提出了建议，并对体育事业和体育产业的进一步研究方向进行了展望。

关键词：世界冠军多元线性回归模型最小二乘法加权最小二乘法

中图分类号：G633.96 文献标识码：A 文章编号：2095-2813（2019）09（c）-0248-09

1 绪论

1.1 问题的提出

改革开放40年来，随着我国社会经济的快速发展和综合国力的增强，我国体育事业得到长足发展，竞技体育取得了历史性突破。国家统计局数据显示，我国在国际体育赛事中冠军人数从1978年的4人稳步增长到2016年的154人[1]。除此之外，在历届奥运会中，我国竞技体育的影响力也在提升。从20世纪80年代到21世纪，金牌数从5～15枚之间增长到25～55枚之间，奖牌数从30枚左右增长到90～150枚之间[1]，金牌榜的排名稳定在世界前3，我国竞技体育在国际上地位已十分稳固。

深入分析我国运动员历年获得世界冠军的情况，应用科学的预测模型，研究影响竞技体育成绩的主要因素，可以对我国体育事业的发展提出合理、有效的决策意见，并对未来发展趋势进行客观的判断，对我国竞技体育的发展具有重大意义。

1.2 研究动态

Bernard、Busse和Lui指出人均GDP、人口规模和主办方是赢得奥运奖牌的重要因素[2]，Johnson和Ali研究了政治因素对奥运会成功的影响[3]。雷桂成以世界上综合国力强的国家为例，研究了奥运会金牌榜（或奖牌榜）与综合国力的关系[4];邓运龙、吴殿廷等研究发现，东道主效应对奥运会成绩有一定的促进作用[5];李力研探讨了人类种族的差异对运动成绩优劣的影响，发现人种特征在一定程度上决定了体育运动成绩[6];王宇鹏从国家宏观角度总结和分析了6个奥运会奖牌榜的影响因素，即国家经济实力、人口数量、东道主效应、人种、文化传统、国家体制[7];赵聂、赵光娟利用时间序列模型对我国年度时间冠军进行了预测研究[8];张玉华利用灰色关联分析法和回归分析法分析了影响世界冠军人数的4个因素[9];冯兴刚等人验证了技术进步有利于提高我国运动水平[10]。

总体来看，虽然国内外的研究成果较多，但是針对我国获世界冠军情况的研究较少;定性分析较多，通过科学模型进行的定量研究较为缺乏;在有限的定量研究成果中，同时进行分析的影响因素较单一。因此，本文在已有研究成果的基础上，构建多元线性回归模型，同时分析我国国际级运动健将人数等7种因素对中国获体育世界冠军情况的影响。

1.3 文章结构

中国体育世界冠军获得情况受众多因素影响，本文主要利用回归分析法，研究中国获体育世界冠军的主要影响因素，以便为我国体育事业发展提供科学有效的决策。

首先，定性分析世界冠军获得情况的影响因素，选取影响较大的因素进行定量分析，建立满足古典假设的经典回归模型[11]。其次，利用收集到的数据样本检验经典模型的基本假设是否成立，若出现违背基本假设的情况，则需要对模型进行适当的修正，并再次检验，直到模型检验通过为止。由此得到优化且修正后的最优回归模型。最后，根据得到的最优模型及以上的分析，对我国体育事业的发展提出合理有效的决策意见，并对未来发展趋势进行客观的预测和判断。

2 模型设定

2.1 世界冠军获得情况的影响因素选择分析

通过对历年中国获体育世界冠军的情况研究，及文献资料的整理，我们发现，我国每年世界冠军获得的影响因素，大致可分为外部因素和内部因素两大方面。

外部因素主要指非自身的环境因素。我国每年世界冠军的获得情况，在大环境上与我国当年的总人口数、国内的生产总值、国际上举行的赛事等有关，本文筛选出我国当年的总人口数和国内生产总值作为大环境中的外部驱动因素研究指标。

从小环境来说，也和国家对体育事业政策上的支持以及倾斜度等有关;另外，随着全民健身的蓬勃发展，由体育事业带动发展起来的体育产业，也是影响运动员水平的外部因素之一;而体育产业的优质资源与条件，较大程度上取决于社会在体育方面的固定投资。因此，本文筛选出体育产业增加值和全社会在体育方面固定资产投资作为小环境中的外部驱动因素研究指标。

在上述外部环境因素的影响下，自身的因素更为重要。自身因素主要体现在两点：运动员的优秀程度和优秀教练员的水平，这两大因素作为内部驱动力可用以下指标数据量化：国际级运动健将人数、二级及其以上运动员人数和各级体育系统职工人数。其中，二级以上运动员有较大的可能获得世界冠军，尤其是国际级运动健将;而健全的体育委员会体系，能为运动健儿们提供更好的训练环境和更科学的技术指导。

综合以上分析，选取我国当年国际级运动健将人数、二级以上运动员人数、各级体育系统职工人数、体育产业增加值、全社会在体育方面的固定资产投资、全国总人口数、当年国内生产总值这7个主要因素，分析我国体育世界冠军的获得情况。

2.2 模式形式设计

根据上文分析，为了研究我国体育世界冠军获得情况的主要影响因素，以我国每年获得体育世界冠军的人数Y作为响应变量，初步选取我国当年国际级运动健将人数X1、二级以上运动员人数X2、各级体育系统职工人数X3、体育产业增加值X4、全社会在体育方面的固定资产投资X5、全国总人口数X6、当年国内生产总值X7作为解释变量。

先通过Y与各因素变量Xi的散点图对数据进行初步探索，观察分析其相关程度。其散点图分别如图1至图7所示。

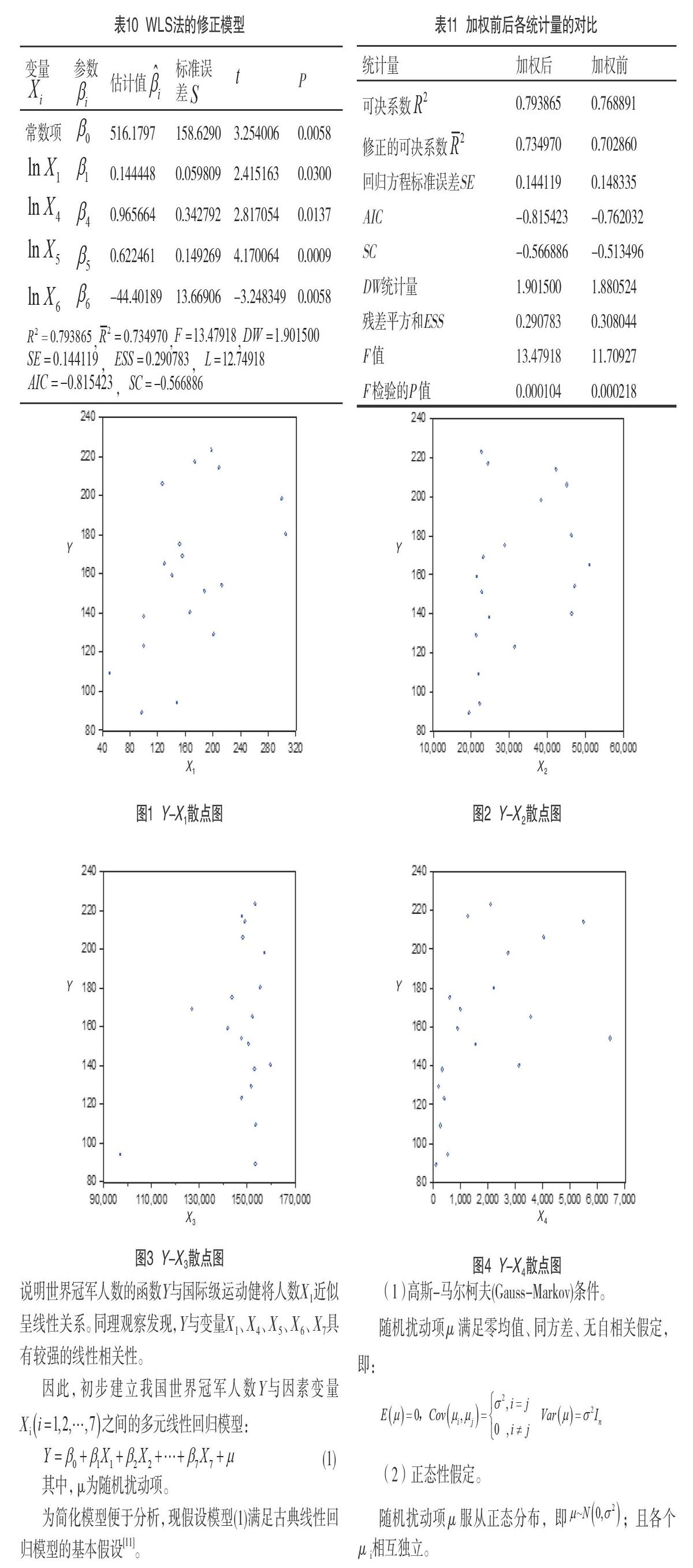
观察图1，发现较大部分点近似在一条直线上下波动，说明世界冠军人数的函数Y与国际级运动健将人数X1近似呈线性关系。同理观察发现，Y与变量X1、X4、X5、X6、X7具有较强的线性相关性。

因此，初步建立我国世界冠军人数Y与因素变量Xi之间的多元线性回归模型：

其中，μ为随机扰动项。

为简化模型便于分析，现假设模型（1）满足古典线性回归模型的基本假设[11]。

（1）高斯-马尔柯夫（Gauss-Markov）条件。

随机扰动项μ满足零均值、同方差、无自相关假定，即：

（2）正态性假定。

随机扰动项μ服从正态分布，即;且各个μi相互独立。

（3）随机扰动项与解释变量不相关假定。

即假定，。

（4）无多重共线性假定。

假定各解释变量之间不存在线性关系，即设计矩阵X满足：

其中，k为自变量个数，n为样本容量。

3 数据准备

根据上文分析及模型的设定，从《中国统计年鉴》中的运动员获世界冠军情况、分地区分技术等级运动员发展情况、体育系统人员机构情况、按主要行业分的全社会固定资产投资、人口数及构成、国内生产总值[1]，以及中国产业信息网的报告《2017年中国体育产业发展近况及产业的经济带动效果》 [12]中获取了所需的数据样本。

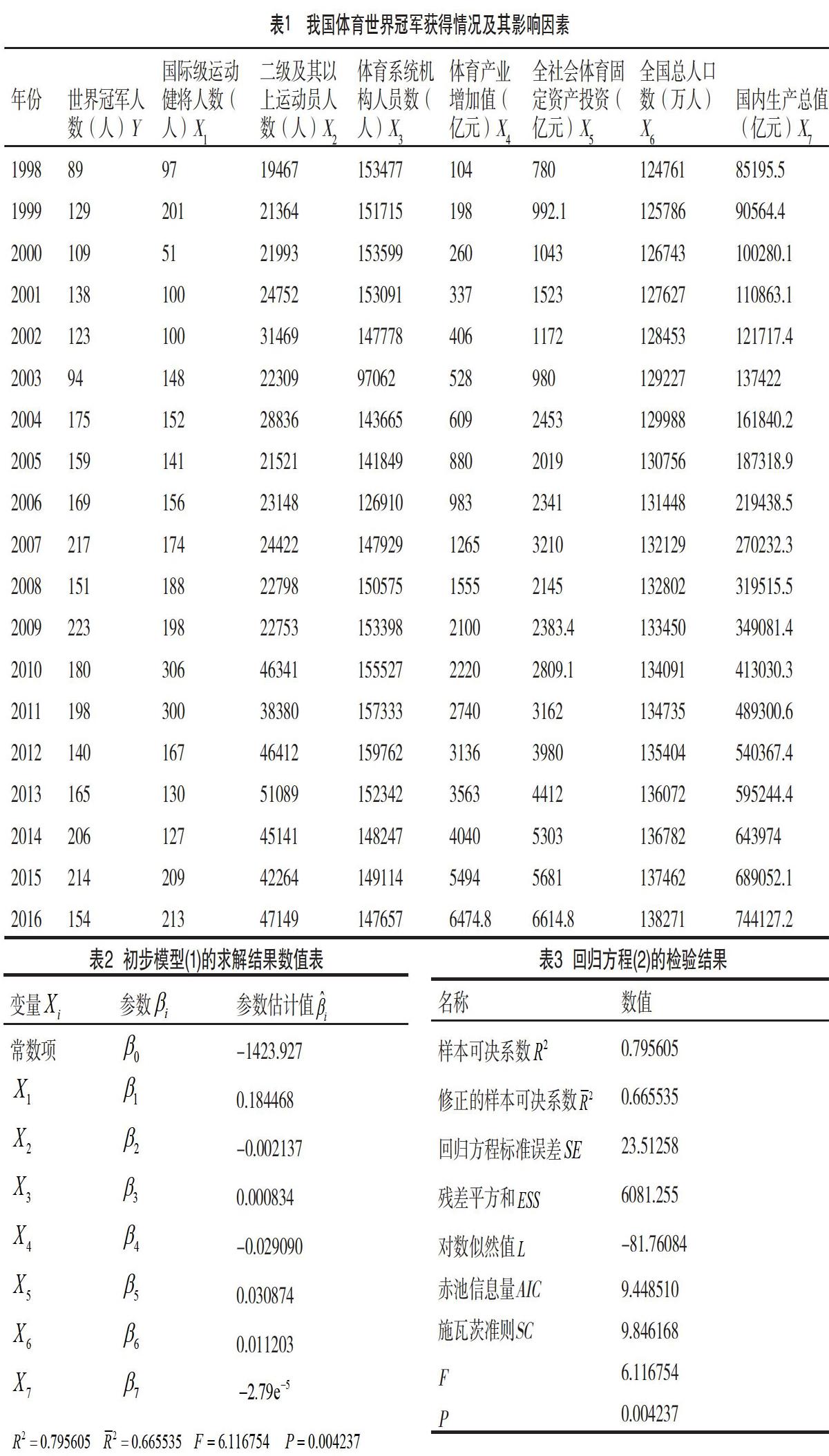
在保证数据完整性与正确性的前提下，选择采用更加完善的数据库，故选用1998—2016年的数据样本。本文获取的数据样本如表1所示。

4 模型求解及优化研究

首先，估计模型中的未知参数，得到预测方程;其次，对拟合模型进行检验，主要包括实际意义检验、统计推断检验以及计量经济学检验（检验是否违背古典假设）;最后，当检验未通过或在检验中发现问题时，需要对模型进行相应的优化与修正。

4.1 初步模型的求解

设定好拟合模型之后，利用序列的样本观察值确定该模型的口径，估计模型中未知参数的值。利用最小二乘法对初步线性回归模型（1）进行参数估计，利用Eviews求解得到模型（1）的回归系数估计值，结果见表2。

从而得到模型（1）的预测方程：

（2）

从表2的回归结果来看，国际级运动健将人数X1对世界冠军人数Y的影响较大。在假定其他因素不变的情况下，国际级运动健将人数X1增加1%，世界冠军人数Y平均增加18.45%;在假定其他因素不變的情况下，全社会体育固定资产投资X5增加1%，世界冠军人数Y平均增加3.09%。这与理论分析和经验判断结果一致。

在确定了拟合模型的口径之后，还要对该拟合模型进行必要的检验。以下主要进行统计推断检验和计量经济学检验这两大方面的检验。

4.2 模型的统计推断检验及优化

统计推断检验主要包括模型系统的显著性检验和回归系数的显著性检验。

4.2.1 模型的显著性检验

选取拟合优度检验和方程的显著性检验对模型系统进行检验。

利用Eviews对回归方程（2）进行检验，结果如表3所示。

通常用可决系数R2度量预测方程（2）的拟合程度。由表3结果可得，可决系数R2=0.795605，调整的可决系数，反映世界冠军人数的79.56%可以由预测方程（2）确定，说明模型对数据样本拟合得较好。

通常使用F检验对模型系统的显著性进行检验。建立原假设：

给定显著性水平α=0.05，构造检验统计量：

得到拒绝域：

由表3结果可得F=6.116754，查F分布表可知，由于，且F检验的P值 P=0.004237<0.05，因此在0.05显著性水平下拒绝原假设，认为回归方程显著，即认为我国当年国际级运动健将人数X1、二级及其以上运动员人数X2、各级体育系统职工人数X3、体育产业增加值X4、全社会在体育方面的固定资产投资X5、全国总人口数X6、当年国内生产总值X7等变量联合起来对我国每年获得体育世界冠军的人数Y有显著影响。

4.2.2 参数的显著性检验

通常使用t检验对回归系数的显著性进行检验。分别建立原假设

给定显著性水平α=0.05，构造检验统计量：

得到拒绝域

利用Eviews对回归方程（2）的回归系数βi，的显著性进行检验，结果如表4所示。

查t分布表可得。结合表4中的结果，发现所有回归系数对应的t值的绝对值都小于2.179，不能拒绝其原假设，认为模型中的7个变量对我国体育世界冠军人数Y都没有显著影响。这与实际情况不符，剖析原因，可能是因为没有进行变量筛选，仅通过定性分析的变量选取方法较为主观，模型中存在不显著变量等原因。

4.2.3 基于逐步回归法的优化模型

针对以上模型的统计推断检验中出现的变量不显著的问题，使用逐步回归法定量地对变量进行筛选。筛选得到变量X1、X2、X3、X4、X5和X6，由此建立优化后的线性回归模型：

（3）

对优化模型（3）进行求解，求解结果如表5所示。

优化模型（3）的回归方程为：

从回归方程（4）来看，国际级运动健将人数X1和全社会体育固定资产投资X5对世界冠军人数Y的影响仍然较大。这与理论分析和经验判断一致，比如在竞技体育中，国际运动健将一般相比其他运动员有更大的可能性赢得世界冠军，因此国际运动健将人数对世界冠军人数具有重要影响。回归方程（4）的决定系数，拟合程度较高，且高于回归方程（2）。

对于模型的检验，查表得。由表5可知，F值满足，方程的显著性检验通过，说明在0.05显著性水平下回归方程（4）显著成立。查表得，对比表4结果，可知方程（4）回归系数的显著情况也得到了极大的改善。

对比初始模型（2）和优化后的回归方程（4）的求解结果，发现相对于初始回归方程（2），优化后的方程（4）的拟合度提高了，F值也提高了，AIC、SC的值都降低了，而回归方程的标准误差SE、F检验的P值、回归系数的标准误差S、t统计量的P值也普遍降低了，都印证了回归方程（4）更优化了。

4.3 模型的计量经济学检验及调整

以上初始模型（1）和优化模型（3）都是在满足基本假设的前提下进行的。但是在实际的计量经济学模型中，违背基本假设的情况时有发生。因此需要对此进行检验和修正，并再次检验，直到通过为止。通常违背基本假设的情况主要包括异方差性、序列相关性、多重共线性。以下主要针对这3个方面进行计量检验。

4.3.1 多重共线性检验

先检验是否存在多重共线性，再使用相关的方法进行修正。

（1）识别。

以下分别使用综合判断法、简单相关系数检验法、判定系数检验法进行多重共线性检验。

首先，进行综合判断。由上回归结果表5中发现，模型（3）的拟合程度较高，整体效果的F检验通过，说明模型对样本拟合的较好，回归方程显著。但有重要变量国际级运动健将人数X1和体育系统机构人员数X3的t检验不显著，模型（3）可能存在严重的多重共线性。

其次，用简单相关系数检验法检验。计算各个解释变量X1、X2、X3、X4、X5和X6两两之间的简单相关系数，得到其简单相关系数矩阵：

由相关系数矩阵可以看出，1解释变量X4和X5、X4和X6、X5和X6之间的相关系数较高，证实部分解释变量之间确实存在较为严重的多重共线性问题。

最后，用判定系数检验法检验。对模型（3）作辅助回归，将每个变量分别作为响应变量对其余5个变量进行线性回归，分别得到它们的判定系数及方差扩大因子，结果如表6所示。

方差扩大因子（Variance Inflation Factor，VIF）是指解释变量之间存在多重共线性时的方差与不存在多重共线性时的方差之比。是容忍度的倒数，VIF越大，显示共线性越严重。经验判断方法表明：当0

（2）修正。

综合以上3种检验的结果，模型中还是可能存在多重共线性的问题。关于多重共线性的修正方法一般有变量变换法、先验信息法、逐步回归法等，本文选取变量变换法和逐步回归法对模型（3）进行修正。

选取对数变换法对模型进行修正。对模型（3）的各变量进行对数变换，得到对数变换模型：

其中，ε为随机扰动项。对模型（5）求解，求解结果见表7。

对数线性模型（5）的回归方程为：

由表7结果可知，F值满足：

方程（6）的显著性检验通过。对比回归方程（4）的求解结果，回归方程（6）的拟合程度R2提高了，AIC、SC的值都降低了，回归方程的标准误差SE也降低了。但是，回归系数的显著性大幅降低了，说明对数变换的方法，对多重共线性的修正效果不太理想。

下面在对数线性模型的基础上，使用逐步回归法对模型（6）进行修正。经过逐步回归法筛选后，剔除了变量和。由此建立新的回归模型：

（7）

其中，ε为随机扰动项。对逐步回归修正模型（7）进行求解，求解结果见表8。

得到逐步回归修正模型（7）的回归方程：

（8）

从回归方程（8）来看，体育产业增加值的对数和全社会体育固定资产投资的对数对世界冠军人数的对数Y的影响较大。这与理论分析和经验判断一致，体育产业的发展情况作为外部因素，是影响运动员水平的外界环境之一;而体育产业增加值和体育方面固定资产的投资情况，反映了我国体育产业的发展情况，因此其对世界冠军的人数也有较大影响。回归方程（8）的决定系数R2=0.769877，拟合程度较高。

对于模型的检验，查表得。由表8可知，F值满足，方程的显著性检验通过，说明在0.05显著性水平下回归方程（8）显著成立。查表得，对比表7结果，可知方程（8）回归系数的显著情况得到了极大的改善，且AIC、SC的值都降低了，回归方程的標准误差SE、残差平方和ESS也降低了，说明误差更小了。

4.3.2 异方差的检验

异方差性指对于给定的每一个自变量Xi，随机扰动项μi的条件方差不等于同一个常数，违背了随机扰动项等方差的基本假定。

（1）检验。

异方差的常用检验方法有：图示检验法、Goldfeld-Quanadt检验法、White检验。其中，Goldfeld-Quanadt检验法只适合大样本量的数据。因此，本文选取图示检验法和White检验法进行异方差检验。

5.3 研究的不足

本文为了便于分析，对模型进行了一定的假设限定，可能与实际情况有些差异。

本文拟合模型的形式设定存在一定主观性，与实际情况不一定相符合。

参考文献

[1] 国家统计局.中国统计年鉴[M]. 北京：中国统计出版社，1999—2017.

[2] Bernard A B，Busse M R.Who wins the Olympic games：economics resources and medal totals [J]. Review of Economics and Statictics，2004（86）：413-417.

[3] Lui Hon-Kwong，Suen Wing.Men，money，and medals： an econometric analysis of the Olympic games[J].Pacific Economic Review，2008，13（1）：1-16.