基于快速MUSIC算法的道路双黄线检测*
2019-11-27张新雨雷海栋王思米1
张新雨,雷海栋,王思米1,2,
(1.西安理工大学晶体生长设备及系统集成国家地方联合工程研究中心,西安 710048;2.陕西省复杂系统控制与智能信息处理重点实验室,西安 710048;3.西安理工大学自动化与信息工程学院,西安 710048)
随着汽车自动驾驶技术的飞速发展,对目标的精准识别对于车辆的自动行驶显得尤为重要,其中包括对道路及道路边沿识别、道路标线识别、行人识别、车辆及车辆类型识别、交通标志识别、障碍物识别和非机动车识别[1-3]。其中对双黄线进行精确检测能够实现车道偏离警告,对于实现车辆的完全自主驾驶,减少事故率有着十分重要的意义[4]。
对双黄线图像进行分割和边缘处理以后,其检测问题就转换成直线检测问题。目前,国内外较为流行的直线检测方法主要有三大类:第一类是最小二乘法[5-6],该方法的原理是根据直线上的点利用解析的方法得到直线参数,它的优点是实时性较好,简单易实现,但缺点是容易受到噪声的影响,同时检测多条直线较为困难。第二类是霍夫变换[7-8](Hough Transform,HT)方法,该方法将提取到的图像特征点转化到参数空间,通过在参数空间里寻找峰值来完成直线检测。虽然该方法的抗噪性好,稳定性高,但其具有高计算量和较长时间成本,无法满足许多实际应用的实时要求。第三类是利用谱估计的方法进行检测[9-10],将含有直线的二值图像转换为虚拟传感器阵列信号,通过构造远场信号模型和近场信号模型,利用谱估计方法分别搜索出直线的倾斜角和偏移量。此类方法分辨率高,抗噪性好,能够快速地同时检测多条直线。多重信号分类(Multiple Signal Classification,MUSIC)算法是一种经典的谱估计方法,由于其具有超分辨率检测精度和良好的抗噪性能被广泛应用[11]。但由于该方法采用对网格逐个遍历的方法,使得检测时间和精度相矛盾。
因此,本文提出了一种基于快速MUSIC算法的直线检测方法。首先,将双黄线图像经过分割和边缘提取,得到双黄线检测的二值图像,然后将其加入独立同分布的高斯噪声转化成多快拍信号,分别构造远场模型和近场模型。其次,基于远场模型先在倾斜角的范围内划分少量网格,利用MUSIC算法搜索到倾斜角的一次估计值,然后在倾斜角一次估计值附近再次划分网格,利用MUSIC算法进一步搜索倾斜角的估计值,从而得到直线倾斜角的估计值。再次,基于近场模型和倾斜角的估计值在偏移量的范围内划分少量网格,同理,分别两次利用MUSIC算法搜索偏移量的估计值,从而检测到双黄线边缘的直线参数。最后利用道路双黄线的图像对本文所提方法进行了有效性验证。
1 问题描述及MUSIC算法
1.1 问题描述
对道路双黄线图像进行检测的原理如下:首先对图像进行分割和边缘提取,得到仅含有双黄线边缘的二值图像,双黄线的边缘为四条直线,对四条直线进行检测即完成对双黄线的检测。假设经过图像分割和边缘检测得到M×M的二值图D,其中,像素值为“1”的点表示直线上的点,像素值为“0”的点表示背景点。如图1所示,建立直角坐标系,假设图像左上角为坐标原点,水平向右为x轴正向,垂直向下为y轴正向,直线上的点满足函数关系

(1)

图1 图像中的直线模型
1.2 MUSIC算法
MUSIC在1979年由Schmidt提出,是一种有效的DOA估计方法[11]。此算法的基本原理是将阵元接收到的数据进行采样,构造出数据的协方差矩阵,并对其进行特征值分解,得到相互正交的信号子空间和噪声子空间。基于这两个子空间的正交特性,构造空间谱函数,通过对谱函数进行谱峰搜索,便可以检测到信号的DOA信息[12-13]。
如图2所示,假设有p个不相关且均值为零的窄带信号si(n),阵列模型由m个等间距阵元构成,其阵元间隔为d。相邻阵元之间由于波程差的存在,而使得接收的信号存在相位差
(2)
式中:λ为信号的波长,d≤λ/2。

图2 均匀线阵远场模型
第m个阵元接收到的信号为
(3)
式中:em(n)为高斯噪声,其均值为零,方差为σ2,a(ψi)=[1,ejωi,…,e-j(m-1)ωi]T。
将式(3)表示为矩阵的形式
X(n)=A(ψ)S(n)+E(n)
(4)
式中:A=[a(ψ1),a(ψ2)…,a(ψi)]T,S=[s1(n),s2(n)…,sp(n)]T,E=[e1(n),e2(n)…,em(n)]T。
信号X(n)的协方差矩阵为
Rx=E[X(n)XH(n)]=A(ψ)E[S(n)SH(n)]AH(ψ)+σ2I=APAH+σ2I
(5)
对Rx数据进行特征值分解,获得特征值和特征向量,并对其按照从大到小的顺序进行排序,前p个大的特征值为信号特征值,后m-p个小的特征值为噪声特征值。由于噪声特征值对应的特征向量En=[vd+1,vd+2,…,vM]与矩阵A的列向量正交,因此可以定义谱函数
(6)
式中:a(ψ)是A的列向量。当矩阵a(ψ)与En的各列互相正交,分母为0,但由于噪声的存在,分母不为0,所以Pmusic(ψ)会有尖峰,因此,从谱峰就可以搜索到波达方向角ψ。
对于均匀线阵近场模型,第m个阵列接收到的信号为
(7)

同理,利用MUSIC算法对近场信号按照上述步骤进行搜索,就可以得到DOA估计值。
2 基于快速MUSIC算法的直线检测
2.1 远场信号模型的建立及直线倾斜角估计
由于MUSIC算法只能处理多快拍信号,因此,需要对原始的含有d条直线的M×M维二值图像D,加入L组服从相同分布、且与信号源无关的零均值高斯噪声,得到的L组图像分别为(D1,D2,…,DL),以构成多快拍信号。
为建立远场模型,首先将二值图像Dk,k=1,2,…,L转换为一维矢量。定义一个向量如下
u=[1,ejμ,ej2μ,…,ej(M-1)μ]T
(8)

然后根据下式将二值图像Dk转换成一维矢量

(9)

a(θi)=[1,ejμtanθi,ej2μtanθi,…,ej(M-1)μtanθi]T
(10)
根据上式,L组二值图像(D1,D2,…,DL)转化为多快拍阵列信号Z=(z1,z2,…,zL)。因为θi具有线性相位特性,信号si可以被视为一个远场信号。
利用MUSIC算法来搜索倾斜角范围。首先根据下式计算出信号的协方差矩阵
Rx=E(ZZH)
(11)
式中:Rx为求得的协方差矩阵。
对Rx进行特征值分解,获得特征值λp和特征向量αp,其中p=1,2,…,M。对特征值按从大到小顺序进行排序,信号子空间对应于d个较大特征值的特征向量,噪声子空间对应于剩余(M-d)个特征值的特征向量。噪声子空间对应的特征向量为噪声特征向量矩阵Gn=[αd+1,αd+2,…,αM]。
假设d条直线的倾斜角范围均为[-90°,90°],首先将[-90°,90°]划分为N1个网格,N1由倾斜角检测分辨率决定,取[1,50]内的整数,则第v1个网格上的角度取值表示如下,其中v1=1,2,…,N1:
(12)
(13)
2.2 近场信号模型的建立及直线偏移量的估计
预先设定参数μ1,μ1≤(π/|tanθi|),且μ1≠μ,将二值图(D1,D2,…,DL)转化成另外一种虚拟阵列信号r=(r1,r2,…,rL)。
(14)
式中:Dk(x,y)为二值图像Dk中(x,y)坐标点的像素值。
根据2.1中远场信号估计出来的入射角,可以将近场模型表示为
(15)
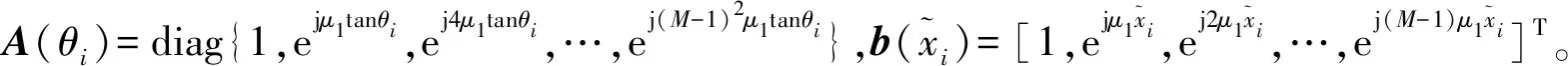
(16)
式中:Bi为虚拟阵列导向矩阵。


图4 经过图像处理后的二值图
3 仿真及结果分析
为验证本文方法的有效性,本文选取两幅道路双黄线图像进行验证,如图3所示。图4为经过图像分割和边缘检测后的图像,由图4可得,经过处理后的双黄线图像共有4条直线。

图3 照相机拍摄的道路双黄线
为验证本文方法的有效性,本次实验将本文结果与手工标定、传统MUSIC[14]和迭代自适应法(Iterative Adaptive Approach,IAA)[15]的结果进行对比。
三种方法算法参数设置如下:(1)IAA和传统MUSIC:d=4,μ=0.6,μ1=0.004;(2)本文方法:d=4,μ=0.555,N1=18,Δθ=10°,N2=20,μ=0.6,倾斜角检测分辨率为1°,μ1=0.003 9,N3=29,N4=20,μ1=0.003 9,偏移量分辨率为1像素点。
仿真结果如图5~图8所示,其中,图5分别为本文方法对图4(a)中四条直线倾斜角估计的功率谱曲线,图6图分别为本文方法对图4(a)中四条直线偏移量估计的功率谱曲线。

图5 图4(a)中四条直线倾斜角的功率谱

图6 图4(a)中四条直线偏移量的功率谱
图7分别为本文方法对图4(b)中四条直线倾斜角估计的功率谱曲线,图8分别为本文方法对图4(b)中四条直线偏移量估计的功率谱曲线。由这些图可得,本文方法具有较强的旁瓣抑制能力和较高的搜索精度。

图7 图4(b)中四条直线倾斜角的功率谱

图8 图4(b)中四条直线偏移量的功率谱
表1、表2为本文方法与其他两种方法的对比结果,由表1、表2可得,本文方法与MUSIC算法都能够精确检测到四条直线的倾斜角和偏移量,而IAA存在一定较小的误差。而由于IAA采用迭代策略,所以时间较长,传统MUSIC算法使用穷举策略,将所有有效范围全部划分网格,增加了搜索时间。本文方法采用两次划分网格的思想,在不降低MUSIC算法检测精度的前提下,将检测速度提高了40%,是一种快速精确的直线检测方法,对自动驾驶的双黄线检测具有重要的意义。

表1 本文与其他两种方法的比较结果(图4(a))

表2 本文与其他两种方法的比较结果(图4(b))
4 总结
本文提出了一种基于快速MUSIC算法的直线拟合方法,基于二值图建立了远场信号与近场信号模型,通过多次划分网格,减少使用MUSIC算法的次数,从而在不变检测精度的同时能够快速地获得双黄线的倾斜角和偏移量的估计值。与传统MUSIC算法以及IAA方法相比较,本文方法速度最快,精度与其他两种相同。因此,本文方法是一种高效的直线检测方法,对汽车自动驾驶偏离车道,减少事故的发生有着重要的实际意义。
