移动WSNs中基于半定规划的节点定位算法*
2019-11-27马佩勋洪贵华
马佩勋,洪贵华
(1.长沙民政职业技术学院软件学院,长沙 410004;2.滇西科技师范学院信息工程学院,云南 临沧 677000)
现多数定位算法只聚集于静态的无线传感网络(Wireless Sensor Networks,WSNs),假定锚节点和传感节点是静态的[1]。当然,通过频繁地更新位置估计,可以将这些定位算法应用于移动WSNs。但是,在设计这些算法时,并没有考虑如何通过移动信息,提高定位精度[2]。
文献[3]研究了节点的移动及移动速度对定位精度的影响。而文献[4]研究了如何利用移动速度估计节点位置。依据通信节点间的测距和相对测速信息,通过扩展卡尔曼滤波(Extended Kalman Filter,EKF)可估计节点位置。
此外,通常利用锚节点与传感节点间的无线信号的一个物理参数或多个物理参数测距。这些参数包括到达时间(Time of Arrival,ToA)[5]、到达时间差(Time Difference of Arrival,TDoA)[6]、接收信号强度(Received Signal Strength,RSS)[7-8]和到达角度(Angle of Arrival,AoA)[9]。其中,基于ToA测距估计精度较高,而基于 RSS测距成本低,易实施。
众所周知,测距信息总是伴随着一些噪声或者不确定信息,这影响了定位性能。而最大似然估计(Maximum Likelihood,ML)是用于克服定位阶段中不确定信息的常用技术。然而,ML估计的计算量大[10]。
利用内点法可将ML问题转化为凸优化问题。而半定规划(Semi-Definite Programming,SDP)[11]和二阶锥规划(Second Order Cone Programming,SOCP)是两个主要的凸优函数。基于SOCP定位系统简单,计算复杂度低。相比于基于SDP定位算法,基于SOCP定位算法的收敛速度更快。但是,基于SDP定位算法的定位精度更高。
为此,针对移动WSNs,提出基于ToA的SDP定位算法SDPL。SDPL算法先利用ToA测距和速度信息,再利用SDP估计节点位置。
1 系统模型
在二维空间内部署na个锚节点和ns个传感节点。所有锚节点和传感节点能够独立移动,从时刻n的位置移动至时刻n+1的新位置,其中n=1,…,N。其中N表示总的观察时刻数。
假定每个传感节点能够测量自己的速度矢量,其包含速率和方向。在两个连续观察时刻内,节点速度保持常量。将节点的速度矢量用于节点的位置估计。

(1)


(2)
式中:R表示节点通信半径。

(3)

2 基于速度辅助的ToA测距定位
假定ToA测距误差服从高斯分布。利用速度信息提高定位精度。考虑两种情况:准确速度信息和噪声速度信息[12]。
2.1 基于准确速度信息的定位
若速度信息准确,则式(1)的模型可修改成:
(4)
将式(4)代入式(3),基于ToA模型可更新为:

(5)

再利用式(6)求解:
(6)
将式(6)分解成多个子问题,并利用传感节点的局部观察求解。这些子问题依赖于邻居锚节点在不同时刻的位置、节点与邻居锚节点间距离以及节点在不同时刻的速度矢量。
令Bi={(j,n)|(i,j,n)∈A}。(j,n)∈Bi意味着在时刻n,锚节点j离传感节点i的距离小于R。具体而言,对于i∈{1,…,ns},传感节点i需解决的子问题:
(7)

(8)
目标函数式(8)是一个非凸优化问题,难以获取其精确解。为此,利用SDP解决此非凸优化问题[13]。
2.2 基于SDP的解
(9)
式中:dk表示矢量d的第k个元素。而rk表示矩阵R的第k个行。
据此,将式(9)可表述以下的约束优化问题:
(10)
式中:w=[w1…wK]T。利用表述式(10)的约束项:
(11)
利用恒等式xTAx=Tr(xxTA),可将式(11)转换成:[W]kk=Tr(DkS),其中k=1,…,K。而W、Dk和S的定义如式(12)、式(13)和式(14)所示:
(12)
(13)
(14)
再利用式(11)~式(14),式(11)的优化问题可表示为:

(15)
2.3 基于噪声速度信息的定位
在实际环境中很难准确地获取节点的速度信息[14]。因此,基于测速误差和测距误差条件下,估计节点位置。式(16)表示了包含测速误差的测速模型:
(16)


(17)
对式(17)进行对数变换,基于ML的定位问题可表述为:
(18)

求解式(18),等价于求解式(19):
(19)
对于任意一个传感节点i,式(19)的第一项为非凸优,而第二项是凸优的,其处理了在不同时刻节点i的测速误差。对式(19)第二项进行扩展,并丢弃常数项。同时,为了简化表述,将下标i删除。最终,可建立式(20)所示的目标函数:

(20)
式中:〈a,b〉=aTb。此外,引入以下标量:
(21)
(22)
式中:Z=STS。
与上节类似,将式(20)转化为SDP松驰的优化问题:
[L]n+1,n+1-2[L]n+2,n+1-2Ts[[L]n+2,1[L]n+2,2]v(n)+
2Ts[[L]n+1,1[L]n+1,2]v(n)}
(23)

3 性能仿真
3.1 仿真环境
利用MATLAB建立仿真平台,并利用MATLAB软件内的CVX工具包[15]。CVX工具包能够计算SDP问题。在方形区域100m×100m内部署锚节点和传感节点。这些节点依据Random-way点移动模型移动。令ϑmin表示节点的最大移动速度。
考虑T=30时刻。节点在每个时刻随机地选择一个目的节点,再移动至此目的节点。并随机选择移动速度进行移动。此外,引用均方根误差(Root Mean Square Error,RMSE)作为性能指标。
本文在第3节分别论述了准确速度信息和噪声速度信息两种环境下的定位问题。为此,接下来分析这两种环境下的SDPL算法的RMSE性能。
3.2 数据分析
3.2.1 基于准确速度信息环境
本小节考虑三类场景。这三类场景参数如表1所示。在这三类场景中,节点的移动的最大速度ϑmin在{1.4,2.8,4.2,5.6,7.0}内变化,且单位为m/s。

表1 场景参数
众所周知,传统的定位算法对测距误差、锚节点数以及通信半径非常敏感。为此,选定三个场景,分析测距误差、锚节点数以及通信半径对定位性能的影响。

图1 RMSE随和ϑmin的变化情况
图2、图3分别显示了锚节点数和通信半径参数对定位算法的影响。观察这两个图不难发现,锚节点数从3增加至6或者通信半径从2 m增加至4 m提高了定位精度。但相比于锚节点数从3增加至6或者通信半径从2 m增加至4 m,移动速度ϑmin从1.4 m/s增加至2.8 m/s时的定位性能更好。

图2 RMSE随锚节点数和ϑmin的变化情况
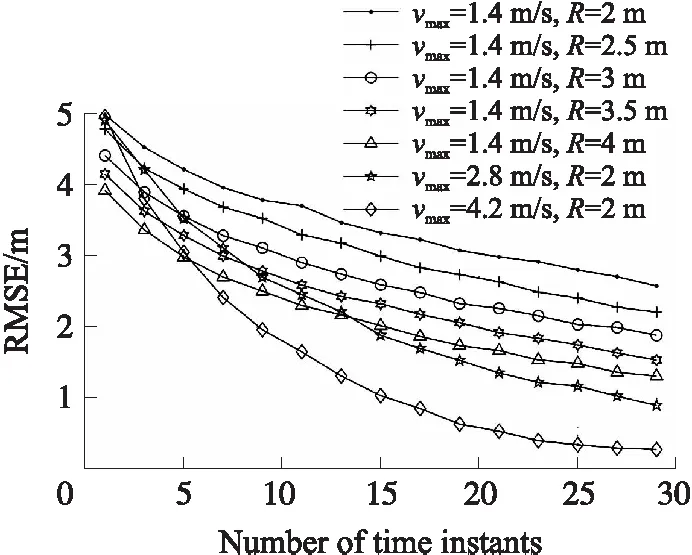
图3 RMSE随R和ϑmin的变化情况
3.2.2 基于噪声速度信息环境
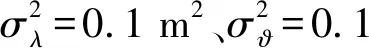

图4 参数ϑmin对RMSE的影响

图5 RMSE随变化情况
4 总结
针对移动无线传感网络的节点定位问题,基于半定规划的节点定位SDPL算法。SDPL算法利用ToA测距,并结合移动节点的速度信息联合估计移动节点位置。同时,考虑准确测速信息和噪声测速信息两种情况。并通过SDP求解基于ML的定位方程。仿真结果表明,相比于锚节点数和通信半径,移动信息对定位精度的影响更大。
