非同步网络中基于TOA的鲁棒非视距目标自定位算法*
2019-11-27朱伟辰
朱伟辰,王 刚
(宁波大学信息科学与工程学院,浙江 宁波 315211)
近年来,各种定位技术在我们的日常生活中发挥了重要作用。目标定位的应用包括导航,目标跟踪,救援,航空航天等[1-4]。基于到达时间(Time-of-Arrival,TOA)的定位方法具有较高的定位精度,在实际环境中十分常用。本文考虑构造目标源自定位问题[5],锚节点在同一未知时间向目标源发送信号,目标源依靠接收信号测量TOA[6]。在这个问题中,目标源不向锚节点发送信号,因而节省了能量并延长了目标源的电池寿命。而且,本方法不要求目标源和锚节点之间保持时间同步[7]。
传感器网络中的时间同步问题对目标定位的精度有着不可忽略的影响,近些年来该问题已经得到了学界的广泛研究[6-11]。在文献[6]中通过目标源接收来自其他锚节点的信号,可以节省目标源的一些能量,并且目标源不需要与其他锚节点保持严格的时间同步。通过使用文献[6]类似的信号收发方式并将时钟偏差当成噪声的一部分进行处理,文献[7]提出一种有效的分式规划(Fractional Programming,FP)方法用于估计目标源的位置。由文献[8]可知,目标源存在的时钟偏差(Clock Skew)和时钟漂移(Clock Offset)是难以处理的参数。最近,文献[9]通过将时钟偏差视为隐藏变量,为异步接收器提出了一种集中的基于期望最大化的被动定位方法,提升了算法性能且可以达到克拉美罗下界。文献[10]采用合作的方式同时完成传感器网络同步和目标源定位的工作,其中目标源之间的协作显著提高了同步和定位的性能。文献[11]提出了一种基于飞行时间(Time-of-Flight,TOF)的方法,该方法通过估计传感器对的相关时钟偏差用于修正TOF测量信息,并引入补偿因子来消除多组传感器对之间的相关时钟偏差从而提高算法的性能。
除了传感器间的时钟同步问题,信号在传播过程中可能被一些障碍阻挡,这种现象被称为非视距(Non-Line-of-Sight,NLOS)信号传播。非视距传播导致信号TOA测量值中存在NLOS误差。各种研究表明,NLOS误差通常远大于测量噪声,这种误差会对算法定位性能有着显著的负面影响[12-16]。一些方法使用非视距误差的分布或统计信息来提升定位精度[12-13]。然而,在时变的实际环境中很难获得这种统计信息。文献[14]提出了一个鲁棒的半正定规划(SDP)方法,无需NLOS误差的统计信息。在文献[15]中,两种对非视距误差具有鲁棒性的方法被提出,即二阶锥松弛(SOCR)和半正定松弛(SDR)方法。这两种方法既不需要路径状态信息也不需要NLOS误差的统计信息,它们只需要实际环境中是较易获得的NLOS误差的上界,并且表现出优于之前非鲁棒方法的性能。通过给定信号到达参考锚节点的时间戳,文献[16]将到达时间差(Time-Difference-Of-Arrival,TDOA)测量模型转化为TOA测量模型,并联合估计目标源发出信号的时间和位置,但该方法在非视距密集环境下定位效果较差。然而,上述文章中研究的定位问题是基于传感器网络完全同步这一条件,并且它们大多不具备目标源自定位的功能。因此,可以看出非同步传感器网络中存在NLOS误差时的目标源自定位问题是一个全新的研究领域。
本文在NLOS条件下解决非同步传感器网络中基于TOA的目标源自定位问题,采用文献[8]和[10]中的测量模型并加入了NLOS误差。模型中存在影响问题求解的参数,例如锚节点开始传输信号的起始传输时间,时钟偏差和时钟漂移。通常,有两种方法可以处理这些参数。一种是联合估计这些参数和目标源位置,另一种是通过模型的转换来消除它们。本文采用后者,通过使用其他测量值减去一个选定的参考测量值,可以消除起始传输时间和时钟漂移而只剩下时钟偏差。经此种处理后,TOA测量值被转换成TDOA测量值。同时经理论分析,可以验证文献[15]中使用的NLOS误差的上界过大,降低了定位性能。为克服该弊端,本文提出了一种新的鲁棒最小二乘(Robust Least Square,RLS)方法,该方法联合估计目标源位置和参考测量值中的NLOS误差,与[15]一样,同样不需要路径状态信息或NLOS误差的统计信息。这种做法将NLOS误差的上界缩小至合理的范围,从而提高了定位性能,然后根据所提出的RLS方法构造了一个非凸最小最大化优化问题。为了求解这个问题,首先应用了三角不等式来消除目标函数中的最大化部分,然后应用半正定松弛(Semidefinite Relaxation,SDR)技术将其松弛为半正定规划(Semidefinite Programming,SDP)问题并进行求解。
1 系统模型
考虑使用k(k=2或3)维定位场景,假设传感器网络中存在N+1个锚节点和一个目标源,其中第i个锚节点和目标源的位置分别由si(i=0,1,…,N)和x表示,x和si都是k维列向量。所有锚节点在同一起始传输时间T0向目标源发送信号,目标源测量并记录各个锚节点发送信号的TOA。假设锚节点之间是时间同步的(目标与锚节点之间不必保持时间同步),且锚节点和目标源之间的传播路径可能是NLOS的。基于上述假设,可将TOA测量模型写为[8]:
(1)

本文的目标是根据模型(1)估计未知目标源位置x,其中ω,T0和θ也是未知的。一种可能的方法是联合估计目标源位置这些未知参数,但太多的优化变量降低了算法的性能[10]。在本文中,我们采用与文献[7]中相同的方法:减去参考测量值并形成TDOA测量值,并通过将编号为0的锚节点指定为参考锚节点,可以将变换后的TDOA测量值表示为:

(2)
式(2)又可改写为如下形式:
di=ω(‖x-si‖-‖x-s0‖+wi-w0+ni),i=1,…,N
(3)
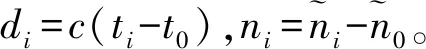
2 鲁棒半正定规划问题的推导
通常时钟偏差ω的值约为1,故本文做出与[6]中相同的假设ω=1+δ,且采用相同的方法来处理δ,即假设δ是随机变量并且服从区间为(-δmax,δmax)的均匀分布,其中δmax是已知常数。通常δ的值远小于1。据此,做出以下近似1/ω=1-δ,模型(3)可近似改写为:
di≈ri-r0+wi-w0+ni+δdi=ri-r0+wi-w0+i,i=1,…,N
(4)
式中:‖x-s0‖=r0,‖x-si‖=ri,i=ni+δdi(i=1,…,N),通过转换δdi可以被视为测量噪声i的一部分。
NLOS误差会对定位性能造成非常显著的负面影响。解决该问题的难点在于NLOS误差的统计信息和信号传播的路径信息通常是未知的,这意味着不能通过将NLOS误差与背景噪声组合从而将式(3)转换为视距(Line-Of-Sight,LOS)模型。文献[15]提出了一种处理NLOS误差方法,该方法仅需要NLOS误差的上界。通常可假设NLOS误差的上界为已知常数,即0≤wi≤i(i=0,…,N),并令ei=wi-w0,可以得到ei的上界为|ei|≤max{0,i}ρi,在[15]文中即对非视距误差ei进行处理。但是,经对该种非视距误差的结构分析,可以得出其上界过大的结论。当参考路径上的非视距误差w0值固定时,分析可得ei实际上落在[-w0,i-w0]的区间内,其区间长度为i。相比之下,[15]中使用的非视距误差区间[-ρi,ρi]的长度是2ρi,明显大于i,故导致了其算法存在额外的性能损失。由此促使本文将未知参考路径非视距误差w0作为变量与目标源位置进行联合估计。

(5)

(6)

(7)
式中:ai和y是N+k+4维列向量,由此可以构造一个最坏情况下RLS问题:
s.t. ‖x-si‖=ri,i=0,…,N
(8)
为求解问题(8),本文使用三角不等式来处理式(8)中的最大化部分:
(9)

s.t. ‖x-si‖=ri,i=0,…,N
(10)
将问题(10)用上镜图的形式等价表述为:
i=1,…,N,
i=1,…,N,
‖x-si‖=ri,i=0,…,N
(11)
式中:η=[η1,…,ηN]T。由式(10)可以看出,问题的目标函数中只有一个绝对值符号从而会产生两个不等式约束,所以该问题的约束数量少于[15]中问题的约束数量,但引入了更多的变量又会增加计算复杂度,具体见后文分析。问题(11)仍是非凸问题,难以求解。利用SDR技术将其放松为以下SDP问题:
(12a)
(12b)
(12c)
i=0,…,N
(12d)
式中:Y(1:k,1:k)表示矩阵Y的第1到k行和1到k列构成的子矩阵,y(1:k)表示y向量的第1到k个元素构成的子向量,而Y(k,k)和y(k)则分别代表矩阵和向量对应位置的元素。其余符号定义如下:
(13)
在文献[15]中已经证明,添加以下二阶锥约束可以改善SDP问题的精确性:
‖x-s0‖≤r0⟺‖x-s0‖≤y(N+k+1)‖x-si‖≤ri⟺‖x-si‖≤y(k+i)i=1,…,N
(14)
此外,根据已知条件0≤w0≤0并通过利用y和Y元素之间的内部关系,我们可以向问题(12)中添加如下约束:
0≤y(N+k+3)≤0y(N+k+2),0≤y(N+k+4)≤0y(N+k+1)Y(N+k+2,N+k+2)=y(N+k+3),Y(N+k+1,N+k+2)=y(N+k+4)
(15)
此外,由于NLOS误差远大于测量噪声[14-15]并且δ很小的事实[6-8],使得条件|i|≪wi成立,并结合式(4),可得如下不等式:
di-ri+r0+w0≥0
(16)
该结果与已知条件0≤w0≤0相结合,可以通过应用重构线性化技术(Reformulation-Linearization Technique,RLT)[17]以构成以下额外约束:
(di-ri+r0+w0)(w0-0)≤0
(di-ri+r0+w0)w0≥0
(17)
进一步,利用y和Y中对应元素重新表示约束(17)为:
diy(N+k+2)-Y(2+i,N+k+2)+y(N+k+4)+y(N+k+3)≤0(di-y(2+i)+y(N+k+1)+y(N+k+2))
(18a)
diy(N+k+2)-Y(2+i,N+k+2)+y(N+k+4)+y(N+k+3)≥0
(18b)
将约束(14),(15),(18)添加到问题(12)中,可得最终SDP问题:
(19)
至此,求解问题(19)即可得目标源的位置估计,为直观展现算法推导递进的过程,本节最后以图表的形式介绍算法的具体实施步骤,内容见表1。

表1 算法流程
3 算法复杂度分析
通常混合SD/SOCP问题的复杂度可通过下式求得[15]:
(20)


表2 算法复杂度
4 仿真结果
在本节中,通过仿真实验对所提出方法与其他方法的定位性能进行比较验证。各锚节点位置在表3中给出,目标源位置从[-50,50]×[-50,50]的正方形区域中随机产生。

表3 锚节点位置

场景一:在这种场景下,固定锚节点的个数为5(N=4),同时设置0=2,i=20α(i=1,…,4)。如图1所示,本文提出方法整体优于其他五种方法,且优势随α的增加愈加明显。具体的,当α=1时,与SOCP-Robust和SDP-Robust相比,本文提出方法的RMSE降低了3.1 m。需要注意的是,当α较大时,SDP-Robust和SOCP-Robust方法中的非视距误差ei大多符号为正,这意味着三角不等式中的等式基本不成立,严重影响了方法性能。随着α的增大SDP-TOA方法的定位精度快速下降,因其需要估计与NLOS误差相关的参数在较大NLOS误差的情况下无法得到精确的估计值。

图1 当α变化,0=2,i=20α时各方法性能对比
场景二:在这种场景下,固定锚节点的个数为5个(N=4),同时设置0=20,i=20α(i=1,…,4)。由图2可知,参考路径上的NLOS误差严重影响了FP和SDP-N方法的定位效果。根据文献[15]可知,SDP-Robust和SOCP-Robust方法直接受到非视距误差ei量级的影响。该场景下,随着α的增加非视距误差ei量级下降但三角不等式中的等式也渐渐无法满足,故造成了SDP-Robust和SOCP-Robust方法定位效果的波动。与其他方法不同,所提出的方法几乎不受参考路径上的NLOS误差的影响。原因是本文将w0作为估计变量同时用鲁棒方法处理NLOS误差。因此,所提出的方法仅受到wi量级大小的影响,仿真结果已经清楚地说明了这一点。同样受到非视距误差wi影响的SDP-TOA方法的定位效果则下降较快,最后在α=1甚的时候甚至比不过SDP-Robust方法,也印证了文献[16]中的结果。
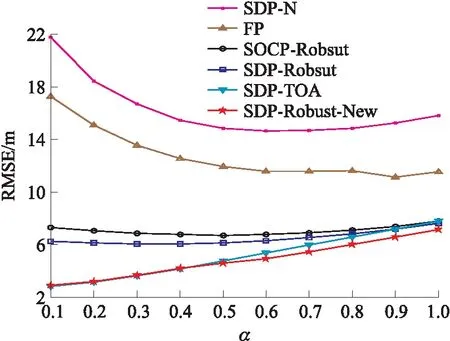
图2 当α变化,0=20,i=20α时各方法性能对比
场景三:在这种场景下,锚节点个数由5增加到9,即N由4增加到8,时设置0=i=20(i=1,…,N)。如图3所示,因为未对非视距误差做出有效处理,在非视距误差较大的环境下FP和SDP-N表现较差。本文提出的方法定位性能随锚节点个数增加而逐渐提升,且仍在定位效果上具有优势。尤其是与SDP-N方法相比,本文方法具有超过6 m的RMSE降低。SDP-Robust和SOCP-Robust方法表现出异常的仿真结果,即随着锚节点个数的增加,性能可能无法稳定提升。此现象可归因于这样的事实:随着锚节点个数的增加,不合适的非视距误差上界问题将对更多测量值产生负面影响。

图3 当锚节点数量N变化时各方法性能对比
5 总结
本文提出了一种新的RLS方法,在非同步网络中对NLOS条件下基于TOA的目标源自定位问题的求解有较好的效果。所提出的RLS方法通过模型转换消去了原模型中存在的一些干扰参数,解决了现有其他方法中存在的不合适的非视距误差上界问题,并挖掘出各优化变量间存在的关系,将这些关系转化为合理的凸约束,因此改善了定位性能。仿真结果证实了该方法的良好性能,并展现了方法对减轻NLOS误差影响的显著效果。
