基于改进ORB算法的双目视觉定位测量方法*
2019-11-27许四祥方建中蔡永祯
杨 宇,许四祥,方建中,蔡永祯
(安徽工业大学机械工程学院,安徽 马鞍山 243000)
现代化钢铁冶金行业中,成型的连铸板坯在运送前需按一定长度切割,火焰切割过程中铁元素会快速与空气中的氧气发生反应生成氧化物,随着熔融钢液蔓延至切割缝下沿,形成一条不规则且硬度较大的钢坯毛刺,若不及时处理,会严重影响轧材的质量和辊道的寿命。本课题组提出了一种等离子去除板坯毛刺的新方法[1],但是由于该系统不能对板坯在辊道上的位置进行实时检测,因此机器人不能按固定工作轨迹切除毛刺,故将其与双目视觉定位与测量系统结合,先对板坯进行定位与测量,再由机器人自主切除毛刺。
在背景复杂的环境中,如何快速寻找和精确匹配特征点成为钢坯定位与测量的难点。在众多特征检测算法中,ORB(Oriented fast and Rotated Brief)算法[2]具有计算量小,匹配速度快等优点,但传统的ORB算法的性能易受环境影响且匹配精度不高,需要进一步提高它的稳定性。邢凯盛[3]等通过提高选取匹配点质量的方式改进随机采样一致性(RANSAC)算法,剔除ORB算法误匹配点,但其特征点检测和描述方法未改变,仍存在误匹配。李卓[4]等采用三元组(LATCH[5])二进制描述子代替传统ORB二进制描述子,提升了描述符的鲁棒性,但特征点检测不稳定,出现误点率高的问题。樊彦国[6]等简化传统ORB算法金字塔模型并优化特征点提取方式,采用梯度方向提取特征点主方向,其算法提高了图像的配准率,但存在多次函数拟合,影响了算法实时性。李佳宽[7]等提出基于ORB特征的水下立体匹配方法,采用水下曲线极线约束,剔除部分误匹配点,该方法显著提升了运算速度,但算法易受环境影响而不稳定。左川[8]等采用加速分割检测(AGAST[9])算法进行特征点提取,利用改进的二进制描述子进行ORB特征描述,提高了特征点的匹配精度和实时性,但该算法在旋转性上还存在一定的不足。
针对上述问题,本文对ORB算法进行改进,首先对特征点邻域内的像素点灰度值进行加权,再采用灰度质心法提取特征点的主方向,以字符串描述子代替传统二进制描述子对特征点进行描述,提升特征点的匹配精度,最后对正确匹配的特征点对的像素坐标进行精确定位,得出特征点的亚像素坐标,依据亚像素坐标对物体进行测量,极大提升测量精度。
1 传统ORB算法原理
ORB是一种快速特征点提取和描述的算法,该算法是FAST(Features From Accelerated Segment Test)特征点检测和BRIEF(Binary Robust Independent Elementary Features)特征描述子的结合,并做了一定的优化和改进[10]。算法核心主要包括:
①特征点主方向计算:传统ORB算法采用FAST算法对图像进行特征点检测,运算速度快且实时性高,但检测的特征点不具有方向属性,传统ORB算法采用灰度质心法计算特征点主方向,实现旋转不变性。
②特征点描述子构建:ORB算法采用二值位描述符形式的BRIEF描述子,以特征点P为中心,定义一个邻域为31×31的补丁区域,在区域内采用高斯随机取样方式选择nd个像素点对,比较每个像素点对间的灰度值大小:
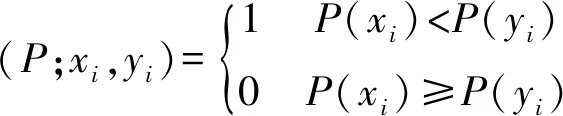
(1)
式中:xi,yi为第i个像素点对的两个像素,P(xi)和P(yi)为两个像素的灰度值。将补丁区域内所有比较结果构建一个nd维特征向量,生成特征点的描述符。

(2)
2 改进的ORB算法
2.1 改进特征点主方向
BRIEF描述子不具备旋转不变性,对特征点进行描述前,需确定特征点的主方向。传统ORB算法采用灰度质心法确定主方向,但计算精度存在误差。考虑到特征点周围的像素的灰度值对特征点的贡献是不同的,距离特征点越近,贡献越大,因此对像素灰度值进行高斯加权处理再通过灰度质心法计算主方向,提高计算主方向的精度,提高配准率。
具体求解步骤为:
①构建一个以特征点P为中心,半径为r的圆形补丁区域。以特征点为原点建立坐标系,遍历补丁区域内每个像素灰度值,使用高斯函数对每个灰度值加权处理,二维高斯函数为:
(3)
式中:σ为标准差,一般取值2s,s为特征点所在的尺度图像的尺度。
②定义补丁区域的矩,如式(4)所示,通过矩得出补丁区域的质心C和特征点的角度θ。
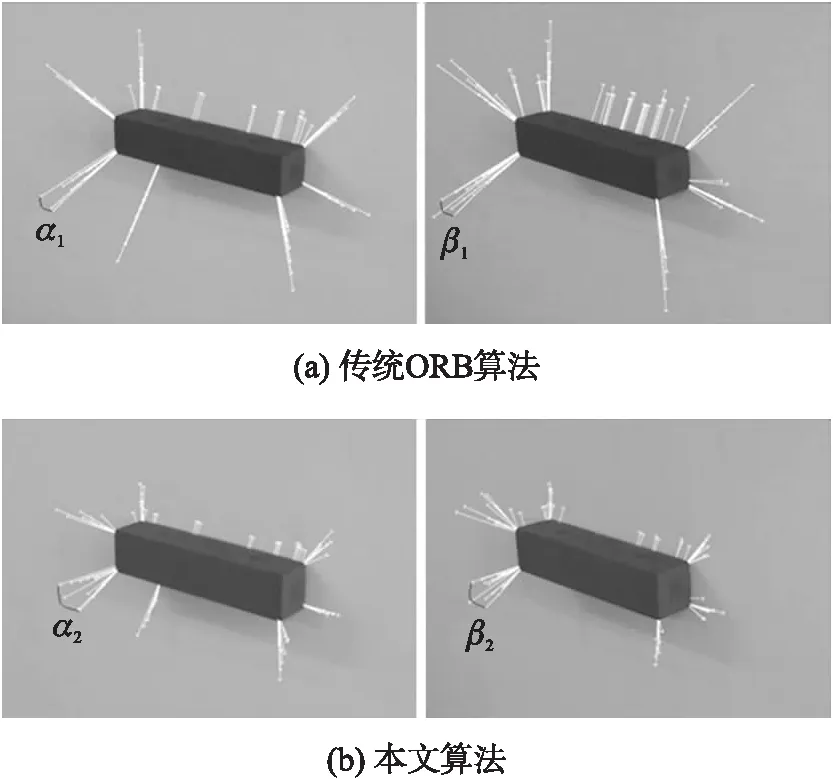
图1 主方向对比示意图

(4)
(5)
(6)
在课题组平行双目视觉定位连铸板坯模型过程中,由于左右相机的人为布置,导致左右两幅图像之间必然存在一定的尺度旋转变化。分别使用传统ORB算法与本文算法求解主方向,对比图如图1所示。图1中两组图片分别为对同一组图像使用传统ORB算法和改进ORB算法计算主方向。以板坯左下角部分特征点为例,由图1可知,角度α2>α1,β2>β1,即改进ORB算法计算出的各特征点主方向方向区间更大,不同特征点主方向更易区分,而传统ORB算法计算的各特征点主方向更聚集,易造成特征点误匹配。
2.2 改进特征点描述子
传统ORB算法采用BRIEF描述子描述特征点,生成一条长度为nd的二进制码,该二进制码为特征点周围nd个点对的比较结果。传统ORB算法采用汉明距离H来判断特征点描述符是否匹配,当汉明距离小于阈值Thanming时,认定两点为匹配点。二进制码描述子缺乏多样性,点对的比较结果单一,较大影响特征点的匹配精度。因此,本文提出对点对的比较结果进行多区间划分,生成一条长度为nd的字符串,使结果呈现更好的多样性,提升特征点的匹配精度,降低阈值Thanming.
具体操作步骤如下:
①实现BRIEF描述符的旋转不变性,需要以特征点为中心的补丁区域旋转角度θ,重新计算补丁区域内部的坐标:(x,y)为旋转前的坐标,(x′,y′)为旋转后的坐标。
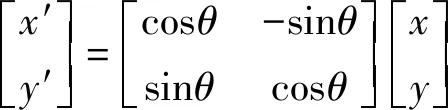
(7)
②采用重新计算后的点对坐标,对应补丁区域内像素的灰度值。分别比较nd对点对的像素灰度值,对比较结果进行如下分析:
将nd个点对(2n个点)组合成一个矩阵A,
(8)
对每一行中两个点对应的像素灰度值进行相减,对得到的差值进行归类,用一个字符表示,生成特征点的描述符。归类算法如下:
t=I(xn1,yn1)-I(xn2,yn2)
(9)
(10)
式中:I(xn1,yn1)和I(xn2,yn2)为点对的灰度值,Valp为特征点P周围点对的比较结果,灰度值差值t的区间可根据环境进行改变。
针对尺度旋转变化与视角变化的板坯模型进行共6组实验,实验结果如图2和表1所示,传统ORB算法匹配精度较差,存在一点多配准现象,其匹配正确率为51.82%,本文改进算法匹配正确率为83.62%,相比传统ORB算法精度提升了30.63个百分点。表明本文改进算法匹配正确率更高。

图2 匹配对比图

组号匹配精度/%传统ORB算法本文算法136.9878.86243.7584.80340.4781.35456.2580.89567.5087.50666.0088.34均值51.8283.62
3 测量实验及结果分析
连铸板坯定位与测量包括相机标定、图像校正、特征点提取与匹配等,其流程如图3所示。为验证本文改进算法的可靠性,通过实验比较传统ORB算法、文献[6]算法及本文改进算法对板坯尺寸的测量精度。
3.1 相机标定与立体校正
本文采用Zhang[11]提出的标定法并结合OpenCV计算机视觉库对相机进行标定[12]。标定板是14×10棋盘格,每格长度为25 mm,使用相机采集24组分辨率为1 920×1 080的标定板照片,标定结果如表2、表3所示,焦距和主点以像素为单位,平移矩阵参数为mm。
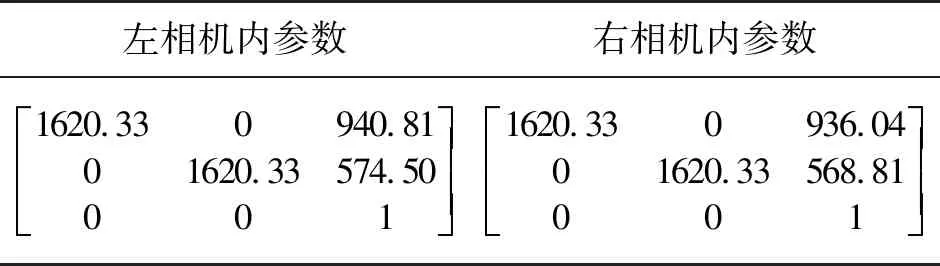
表2 相机内参数标定结果

表3 相机外参数标定结果
标定结果最大重投影误差为0.59pixels,平均重投影误差为0.42pixels。基于标定结果,对采集的板坯进行畸变校正和极线校正,校正前后的图像效果图4所示。

图4 立体校正前(上)和立体校正后(下)
3.2 匹配与测距
对校正后的左右连铸坯图像,采用本文改进的ORB算法对左右图像进行特征点检测、描述并匹配。
检测特征点时,FAST算法会计算每一个特征点的得分值,即每个角点的角点响应值V,根据角点响应值对角点进行非极大值抑制,排除多个特征点聚集在一起的问题。传统非极大值抑制方法是把角点的灰度与它邻近的圆周上16个像素点的灰度值的差值的绝对值之和作为角点响应值V,在3×3领域内比较V值,保留比其8邻域都大的像素作为最终的特征点。
筛选出测量需求的匹配点对,以这些特征点为中心,在其3×3邻域内进行二维二次函数的最小二乘法拟合,计算出邻域内最大得分值,以及该得分值所对应的亚像素级坐标。以特征点为原点(0,0)建立坐标系,x,y表示像素的横、纵坐标,z轴为像素得分值,3×3邻域内其他8个像素的坐标分别为(-1,-1),(-1,0),(-1,1),(0,-1),(0,1),(1,-1),(1,0),(1,1),这9个像素的得分值分别为V1,…,V9。
设二维二次函数为:
z=a1x2+a2y2+a3x+a4y+a5xy+C
(11)
(12)
极大值处的坐标(x′,y′)相对于特征点(x,y)的偏移量为(Δx,Δy)。选取左右图像匹配点对,采用上述方法得出特征点的亚像素坐标,计算特征点的视差,根据三角测量原理,得出该点的三维坐标。预测点如图5所示,筛选出的匹配点对如图6所示,关键特征点在左右图像中的像素坐标和空间坐标如表4所示。

图5 板坯左图像测量点

图6 板坯测量匹配点对

表4 角点坐标
4 实验结果分析
4.1 测量精度分析
实验中被测板坯模型尺寸为300 mm×67 mm×63 mm,测量模型尺寸如表5所示。

表5 传统算法测量板坯尺寸结果
从表5中可以得出,连铸板坯模型三条边的计算尺寸最低误差为0.42%,最高误差为1.93%,平均误差为1.35%,绝对误差保持在1.2 mm左右,均在误差允许范围内,而AB与BC边的相对误差较大,这与板坯角点不够明显,检测出的特征点和理想角点有一定偏差有关。其反映在图像上的像素偏移在各条边产生的绝对误差几乎相同,但相对误差区别较大。还需进一步提升测量精度。
4.2 对比分析
实验测试配置:Inter 酷睿i5 4210U处理器,内存8GB。改变双目相机与板坯的相对位置,对板坯拍摄三组不同视角的图像,分别比较传统ORB算法、文献[6]改进ORB算法和本文算法的测量误差、匹配时间。由表6~表8中多组实验数据对比可得,传统的ORB算法运算速度最快,其次是本文算法,文献[6]改进算法存在多次拟合函数,速度最慢,本文算法在测量阶段需要对精确的特征点像素坐标进行拟合,故速度比传统ORB算法稍慢。从测量精度考虑,本文算法测量误差最低,平均测量精度为0.48%,而传统ORB算法结果误差为2.17%,提升了1.69%,与文献[6]算法相比也提升了0.8%,因此本文改进算法在传统ORB算法基础上有很大的提升。

表6 传统算法

表7 文献[6]算法

表8 本文算法
5 结论
论文针对基于传统特征点检测的双目视觉测量中匹配时间长、误匹配率高和测量精度低的问题,提出一种应用到双目视觉测量中的改进ORB算法。该算法对特征点邻域内像素灰度值进行加权改进传统灰度质心法,同时以字符串描述子代替传统的二进制描述子对特征点进行描述,最后利用二维二次函数拟合对特征点进行定位。通过实验对比分析,本文改进算法在满足尺度和旋转不变性要求下,具有更高的正确匹配率,同时特征点采用亚像素定位,提高了双目立体视觉定位和测量的精度,为后续机器人自主去除毛刺提供了依据。
