Forced Vibration of the Non-Homogeneously Pre-Stressed System Consisting of the Hollow Cylinder and Surrounding Medium

SurkayD.AkbarovandEminT.Bagirov

Abstract: The paper deals with the study of the influence of the non-homogeneous prestresses in the system consisting of the hollow cylinder and surrounding elastic medium on the frequency response of this system caused by the time-harmonic ring load acting in the interior of the cylinder.The axisymmetric problem is considered and it is assumed that in the initial state,the system is compressed in the radial direction with homogeneously distributed static forces as a result of which,non-homogeneous pre-stresses (or initial stresses)appear in that.It is also assumed that after these pre-stresses appear in the interior of the cylinder,the point-located (with respect to the axial coordinate directed along the cylinder’s central axis)additional time-harmonic ring load acts.Thus,it is required to determine how the pre-stresses influence the frequency response of the system to the noted additional time-harmonic loading.This influence,which is the non-linear effect,is studied within the scope of the so-called three-dimensional linearized equations and relations of the theory of elastic waves in pre-stressed bodies.The solution to the corresponding boundary value problems is found by employing the discrete analytical solution method and numerical results on the influence of the pre-stresses on the frequency response of the interface stresses which appear as a result of the action of the additional time-harmonic forces,are presented and discussed.In particular,it is established that the pre-stresses mentioned above cause to decrease the magnitude of the interface dynamic stresses appearing as a result of the additional time-harmonic loading.

Keywords: Non-linear effect,inhomogeneous initial stresses,frequency response,timeharmonic ring load,hollow cylinder,surrounding medium.

1 Introduction

The more detailed and fundamental investigations of the dynamic problems regarding underground structures which,as usual,are modelled as a hollow cylinder surrounded with an elastic medium,requires to be taken into consideration the non-linear effects caused by the reference particularities of these structures,one of which are the non-homogeneous prestresses appearing as a result of the earth’s gravity.Such studies relate to the mechanics of underground structures which contain pipelines,tunnels,subway lining and mine workings as well as other similar structures.

At present,such structures are constructed at deeper depths,according to which,within them appear non-homogeneous initial stresses (or pre-stresses)with considerable magnitude caused by the Earth’s gravity and the magnitude of these stresses may be so great that they must be taken into consideration in understanding the dynamics of these structures.In other words,it appears necessary to consider the pre-stressed under the study of the dynamic problems for the underground structures.The present paper is concerned with the study of one such problem,namely,the study of the influence of the nonhomogeneous pre-stresses in the system consisting of the hollow cylinder and of the infinite elastic medium surrounding this cylinder to the frequency response of this system to the time-harmonic ring load acting in the interior of the cylinder.It is assumed that the initial stresses appear as a result of the action of the axisymmetric static radial forces acting at infinity and the time-harmonic dynamic forces are taken as additional ones concerning the forces which cause the pre-stresses.

It should be noted that the mathematical modelling of these problems cannot be made within the scope of the classical linear elastodynamics,consequently,for such modelling,it is necessary to employ the geometrically non-linear theory of elasticity,the solution of which is very difficult.Therefore,as usual,for mathematical modelling of such problems,the threedimensional linearized theory of elastic waves in pre-stressed bodies is used,the equations and relations of which are obtained through the linearization of the corresponding geometrical non-linear theory of elastodynamics.Moreover,note that the results obtained within the framework of the three-dimensional linearized theory are valuable in the cases,where,in the linearization procedure the higher-order terms can be neglected with respect to the first-order terms,and the possibility of neglecting them requires certain restrictions on the magnitude of the additional dynamic forces with concerning to the magnitude of the initial static ones.Despite this simplification,the influence of the pre-stresses on the stressstrain state caused by the additional dynamic forces can be taken into consideration through these linearized equations.Consequently,the linearized equations mentioned above can be taken as the first iteration under solution of the geometrical non-linear equations of elastodynamics (if the initial stress-strain state are taken as the zeroth iteration),and the problem studied in the present work and described via these linearized equations is a nonlinear one in its physico-mechanical nature.Note that such an approach is also used in the papers by Mohabuth et al.[Mohabuth,Kotousova and Ng (2016)],Vinh et al.[Vinh,Anha,Merodiob et al.(2018)] and in many others listed therein.

Despite the significance of the related investigations,up to now such investigations,i.e.investigations regarding the dynamics of the structural elements with non-homogeneous pre-stresses are almost completely absent (except for a few works carried out in the investigations [Engin and Suhubi (1978);Shearer,Abrahams,Parnel et al.(2013);Wu,Su,Liu et al.(2018);Akbarov and Bagirov (2019);Bagirov,Akbarov and Seyfullayev (2018)].Notwithstanding this,the corresponding problems related to the stability loss of mine workings with inhomogeneous initial stresses have been studied by Guz and his students,the results of which are detailed in the monograph by Guz [Guz (1977)] and a review of which is given in the paper by Guz [Guz (2003)].At the same time,it should be noted that in these investigations,the mine workings are modelled as an infinite homogeneous elastic or elastoplastic medium containing a cylindrical cavity and having initial nonhomogeneous axisymmetric stresses and the variational method is developed for the solution to the corresponding eigenvalue problems.

Now we attempt to detail the investigations made in the aforementioned works [Engin and Suhubi (1978);Shearer,Abrahams,Parnell et al.(2013);Wu,Su,Liu et al.(2018);Akbarov and Bagirov (2019);Bagirov,Akbarov and Seyfullayev (2018)].Note that in the papers [Engin and Suhubi (1978);Shearer,Abrahams,Parnell et al.(2013)],torsional waves in the hollow cylinder made of incompressible highly elastic materials are studied and it is assumed that the non-homogeneous pre-stresses therein are caused by static internal and external uniformly distributed compressional radial forces.Unlike the foregoing papers,the paper by Wu et al.[Wu,Su,Liu et al.(2018)] has studied the longitudinal axisymmetric wave propagation and dispersion in the hollow cylinder made of functionally graded highly elastic material.As in the previous last two papers,this study is also made for the case where the cylinder is pre-stressed with the compressional uniformly distributed forces acting on the internal and external face surfaces of the cylinder.Concrete numerical results in all three papers are obtained for Mooney-Rivlin strain energy function.

Note that in the paper by Engin et al.[Engin and Suhubi (1978)] (as in the paper by Shearer et al.[Shearer,Abrahams,Parnell et al.(2013)]),the initial stress-strain state is determined almost elementary without any difficulty.For the solution to the corresponding linearized wave propagation equations the paper by Engin et al.[Engin and Suhubi (1978)] employes the Frobenius method as well as the variational approach,and the concrete numerical results obtained within each approach are compared with each other.However,for the solution to the mentioned wave propagation equations the paper by Shearer et al.[Shearer,Abrahams,Parnell et al.(2013)] employs the Liouville-Green method.Numerical results presented and discussed in these works illustrate the influence of the non-homogeneity of the pre-stresses on the torsional wave dispersion propagated in the hollow cylinder.

In the case considered in the paper by Wu et al.[Wu,Su,Liu et al.(2018)],the analytical determination of the initial stress-strain state is more difficult,and separate works,such as the papers by Batra et al.[Batra and Bahrami (2009)] and Chen et al.[Chen,Liu,Kitipornchai et al.(2017)],are devoted to this determination.Consequently using the results obtained in these works,the paper by Wu et al.[Wu,Su,Liu et al.(2018)] solves the wave propagation equations by utilizing the state-space formalism for these equations with the approximate laminate or multi-layer technique.

The paper by Akbarov et al.[Akbarov and Bagirov (2019)] studies the longitudinal axisymmetric wave dispersion in a bi-layered (bi-material)hollow cylinder with nonhomogeneous pre-stresses caused by the hydrostatic pressures acting on the faces of that.For the solution to the corresponding field equations,the discrete analytical method is employed and numerical results on the influence of the mentioned non-homogeneous pre-stresses on the dispersion of the longitudinal axisymmetric waves are presented and discussed.

In the work by Bagirov et al.[Bagirov,Akbarov and Seyfullayev (2018)],the dynamics of the moving ring load acting in the interior of the cylindrical cavity contained in the infinite elastic medium with non-homogeneous pre-stresses is studied.Under this study,it is assumed that the pre-stresses are caused with the uniformly distributed normal forces acting at infinity in the inward radial direction.

Now we consider a brief review of the investigations related to the dynamics of the system consisting of the hollow cylinder and surrounding elastic medium which have been made by utilizing the classical linear theory of elastodynamics.Among these investigations,we can select the papers [Pozhuev (1980);Abdulkadirov (1981);Chonan (1981);Hasheminejad and Komeli (2009);Hussein,François,Schevenels et al.(2014);Yuan,Bostrom and Cai (2017)] and others listed therein.

Chonan [Chonan (1981)] studied the dynamics of the axisymmetric moving ring load acting in the interior of a cylindrical shell surrounded with an infinite elastic medium.Under this study,the motion of the shell is described within the scope of thick shell theory,however,the motion of the surrounding elastic medium is described by the exact equations of linear elastodynamics and it is assumed that the cylindrical shell and surrounding elastic medium are joined through a thin elastic bond.Numerical results on the critical velocity of the moving load and on the radial displacement of the shell are presented and discussed.The paper by Pozhuev [Pozhuev (1980)] also studied the dynamics of the axisymmetric moving load acting in the interior of the cylindrical shell surrounded with an elastic medium,however,it is assumed that the material of the surrounding elastic medium is transversally isotropic,the symmetry axis of which coincides with the central axis of the cylinder.Some numerical results on the radial displacement of the shell and on the radial stress acting between the shell and surrounding medium are presented,but numerical results on the critical velocity of the moving load are not presented.

The critical velocity of the moving ring load acting in the interior of the cylinder surrounded with elastic medium was also considered in the paper by Abdulkadirov [Abdulkadirov (1981)],in which,unlike the foregoing papers by Chonan [Chonan (1981)] and the paper by Pozhuev [Pozhuev (1980)],not only the motion of the surrounding elastic medium but also the motion of the cylinder is written with the exact equations of elastodynamics.Numerical results on the critical velocity are obtained through analyses of the corresponding dispersion curves.

The paper by Hasheminejad et al.[Hasheminejad and Komeli (2009)] investigated the dynamics of the axisymmetric moving load which acts in the interior of the hollow cylinder surrounded with the fluid-saturated infinite poroelastic medium.The motion of the fluidsaturated permeable medium is described by Biot’s dynamic theory of poroelasticity and it is assumed that the cylinder and the surrounding medium is connected through the thin massless viscoelastic bond.It is assumed that there exist discontinuities across the viscoelastic bond of the radial and axial displacements of the cylinder and of the surrounding medium and thetype differential operator is used (wherea1anda2are constants andtis the tıme),in order to express the interface stresses through the corresponding displacements’ discontinuities.Numerical results are considered for the radial displacements of the cylinder’s wall and of the porous soil at the interface points and under this consideration,attention is focused on the influence of the foregoinga1anda2constants on these displacements.

There are also a certain number of investigations (see,for instance,the investigations carried out in the papers [Hussein,François,Schevenels et al.(2014);Yuan,Bostrom and Cai (2017)] and others listed therein)in which mathematical methods are developed for the solution to more complicated problems related to moving load dynamics acting in the interior of the hollow cylinder embedded in an infinite layered medium (see,for instance,the paper by Hussein et al.[Hussein,François,Schevenels et al.(2014)])and semi-infinite homogeneous elastic mediums (see,for instance the paper by Yuan et al.[Yuan,Bostrom and Cai (2017)]).Note that in these works,numerical results are presented only for the vibration of the surrounding mediums caused by the moving load.

In recent years,series papers by Akbarov and his students was published (for instance,in the papers by Akbarov et al.[Akbarov and Mehdiyev (2017,2018a,2018b,2018c);Akbarov,Mehdiyev and Ozisik (2018);Ozisik,Mehdiyev and Akbarov (2018)] and others listed therein)in which the dynamics of the moving and oscillating moving load acting in the interior of the hollow cylinder surrounded with elastic medium were investigated and these investigations were made within the scope of the exact equations and relations of classical linear elastodynamics (except the paper by Akbarov et al.[Akbarov and Mehdiyev (2018a)].However,in the paper by Akbarov et al.[Akbarov and Mehdiyev (2018a)],the problem of the moving axisymmetric ring load is investigated for the initially uniaxial homogeneously stressed hollow cylinder surrounded with the initially uniaxial homogeneously stressed elastic medium within the scope of the three-dimensional linearized theory of elastic waves in pre-stressed bodies.It is assumed that these homogeneous uniaxial initial stresses appear as a result of the action of the uniformly distributed normal forces acting at infinity in the cylinder’s central axis direction.It should be noted that within this framework a lot of investigations were made regarding the study of the wave propagation in tubes,plates and cylinders,a consideration and review of which are made in the works [Guz (2004);Li,He,Mangan et al.(2017);Akbarov (2015)] and others listed therein.Moreover,we note that in the foregoing works,not only axisymmetric but also non-axisymmetric 3D (see,the papers by Akbarov et al.[Akbarov and Mehdiyev (2018b);Akbarov,Mehdiyev and Ozisik (2018)] dynamic problems were investigated.

This completes the consideration of the review of related investigations and finally,note that the problem which was indicated in the beginning paragraphs of the present section,i.e.the problem related to the forced vibration of the inhomogeneous initially stressed hollow cylinder surrounded with the non-homogeneous pre-stressed infinite elastic medium under action in the interior of the cylinder,the time-harmonic point-located (with respect to the cylinder’s axis)forces,in the case where the pre-stresses are absent,were investigated in the paper by Akbarov et al.[Akbarov and Mehdiyev (2017)].Therefore,the investigations carried out in the present paper can also be considered as generalization and development of the investigations carried out in the paper by Akbarov et al.[Akbarov and Mehdiyev (2017)] which was made within the framework of classical linear elastodynamics.

2 Formulation of the problem

We introduce to the consideration a bi-material elastic system consisting of the hollow cylinder with thicknesshand surrounding elastic medium,schematically shown in Fig.1 and assume that the external radius of the cross section of the cylinder isR.We differentiate the following three states in this system:the natural state (the first state),initial state (second state)and perturbed state (third state).Taking into consideration the nonexistence of any stresses and strains in the system in the natural state,we assume that in the initial state this system is loaded at infinity with uniformly distributed normal radial static forces with intensityqacting in the radial inward direction.We call these forces as the initial forces and the stress-strain state caused by these forces as the initial stress-strain state in the system under consideration and note that such initial loading can be taken as modelling of the appearing of the stress state in the underground structures as a result of the earth’s gravity.

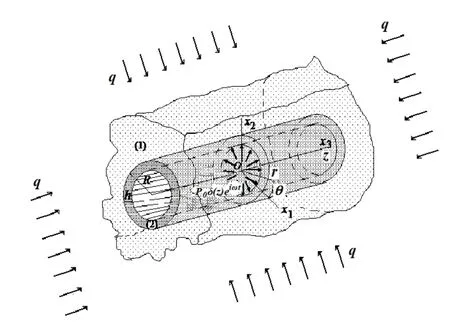
Figure 1:The sketch of the system consisting of a hollow cylinder and surrounding elastic medium and external forces acting on this system

Finally,we suppose that after these initial stress-strain states appear,in the interior of the cylinder,the additional (with respect to the initial loading)axisymmetric dynamic timeharmonic ring load acts,and as a result of this loading,the third state (i.e.,the perturbed state)appears in the system under consideration.

The main question in the present investigation is to determine how the initial stresses (or pre-stresses)influence the dynamic stress-strain field appearing as a result of the action of the noted-above additional time-harmonic ring load (i.e.,the dynamic stress-strain field appearing in the third perturbed state).To study this question,we use the three-dimensional linearized theory of elastic waves in pre-stressed bodies,the field equations and relations of which are described in the monographs [Guz (1977,2004);Eringen and Suhubi (1975);Akbarov (2015)] and in many others listed therein.Note that the equations and relations of this three-dimensional linearized theory are obtained from the corresponding geometrical non-linear equations and relations through their linearization with respect to the quantities appearing as a result of the action of the additional time-harmonic ring load.

Thus,within the framework of the foregoing assumptions,we attempt to investigate the aforementioned question and first,we associate the Cartesianand cylindricalOrθzcoordinate systems (Fig.1)with the central axis of the cylinder and the position of the points of the constituents we determine with the Lagrange coordinates in these coordinate systems.

For distinguishing the values related to the cylinder and surrounding elastic medium we use the upper indices (2)and (1)respectively,and the values related to the initial stresses we indicate by the additional upper index 0.

For determination of the initial stress state we employ the classical linear theory of elasticity and the expressions for the stresses obtained as a result of this determination,which are detailed in many monographs and textbooks regarding the classical linear theory of elasticity,can be presented as follows:

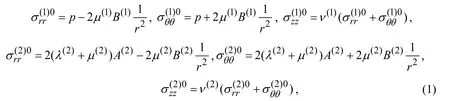
whereλ(n)andµ(n)are the Lame constants andν(n)is Poisson’s ratio of then-thmaterial.The unknown constantsB(1),A(2)andB(2)in (1)are determined from the following equations,which are obtained from the corresponding boundary and contact conditions satisfied under determination of the initial stresses.

Thus,the pre-stresses in the system under consideration are determined through the expressions in (1)and (2).For investigation of how these pre-stresses influence the dynamics of this system in the case where,in the interior of the cylinder,the additional time-harmonic ring load acts,we employ the 3D linearized theory of elastic waves in prestressed bodies.According to the monographs by Guz et al.[Guz (1977,2004);Eringen and Suhubi (1975);Akbarov (2015)] and others listed therein,the field equations of this theory for the case under consideration can be written as follows.

The equations of motion:

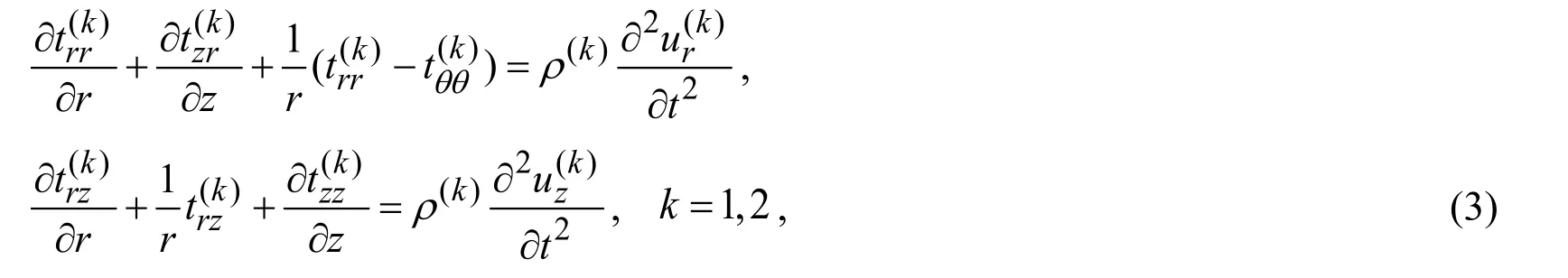
where

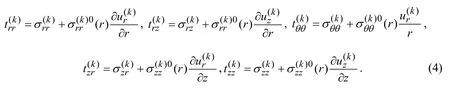
The elasticity and strain-displacement relations:

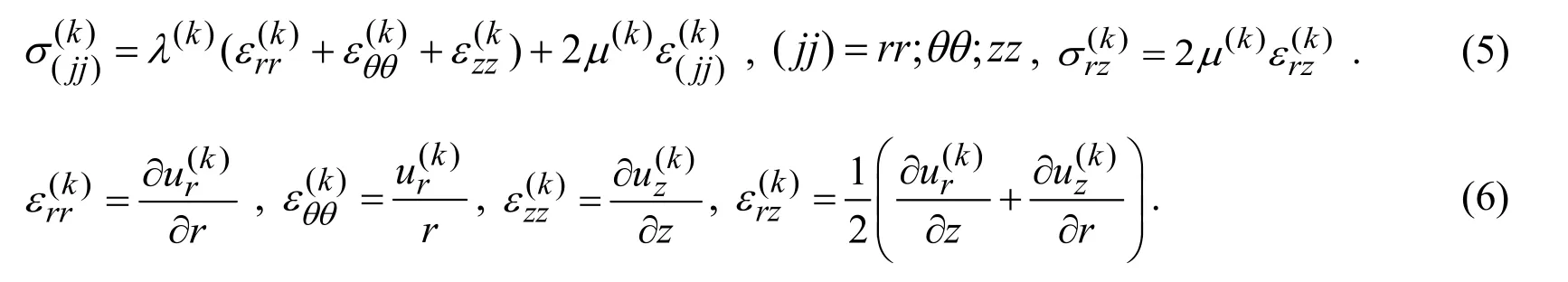
We formulate also the corresponding boundary and contact conditions.The boundary conditions in the interior of the cylinder and the decay conditions at infinity can be written as below.

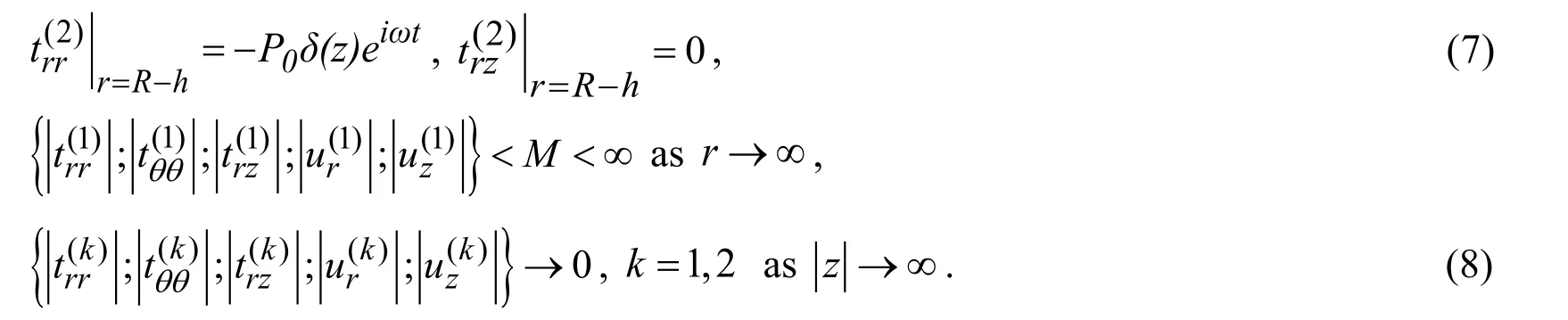
We also assume that the following perfect contact conditions on the interface between the cylinder and surrounding elastic medium are satisfied.

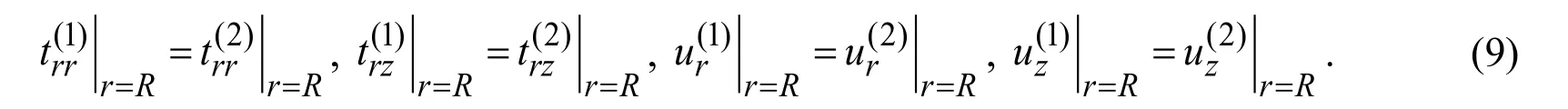
Thus,the mathematical modelling of the influence of the non-homogeneous initial stresses determined with the expressions (1)and (2)in the system under consideration on the dynamic stress field appearing as a result of the action of the time-harmonic ring load acting in the interior of the cylinder is reduced to the solution to the system of Eqs.(3)-(6)within the scope of the boundary conditions (7)and (8)and the contact conditions in (9).

It should be noted that under obtaining the linearized Eqs.(1)and (2)and the corresponding boundary conditions with respect to the forces in (7)from the corresponding geometric non-linear equations and relations,it is assumed that the higher order terms of the perturbed state can be neglected with respect to the corresponding linear order terms.Consequently,the linearized equations and relations can be taken as the first iteration under the solution procedure of the non-linear equations,and the results obtained within the framework of the linearized equations have accuracy with the orderO(p/q).Thus,we can conclude that in the quantitative sense,the results on the non-linear effects obtained within the framework of the linearized equations can be applied in the cases wherep≪q.However,in the qualitative sense,the results on the non-linear effects obtained within the framework of the linearized equations can be used in the larger diapason of the ratio / .p q

This completes the formulation of the problem.

3 Method of solution

In the present section,we attempt to develop the discrete-analytical method for the formulated problem,according to which,the solution region with respect to the coordinateris divided into sub-regions in each of which the pre-stresses are taken as constant ones.For the solution to the corresponding equations in each sub-region,we employ the classical Lame decomposition and Fourier transform with respect to the axial coordinatez.We begin the consideration of the solution method with the obtaining corresponding equations for the potentials which enter into the Lame decomposition.

3.1 Employing of the Lame decomposition and the Fourier transform

As noted above,for the solution to the considered problem,we use the classical Lame decomposition (see,for instance,the monograph by Eringen et al.[Eringen and Suhubi (1975)])which for the case under consideration (i.e.,for the axisymmetric case)can be presented as follows.

Substituting expressions in (10)into the expressions (6),(5)and (4)and doing some cumbersome mathematical manipulations we obtain the following equations for the potentialsΦ(k)andΨ(k)from the equations in (3)-(6).

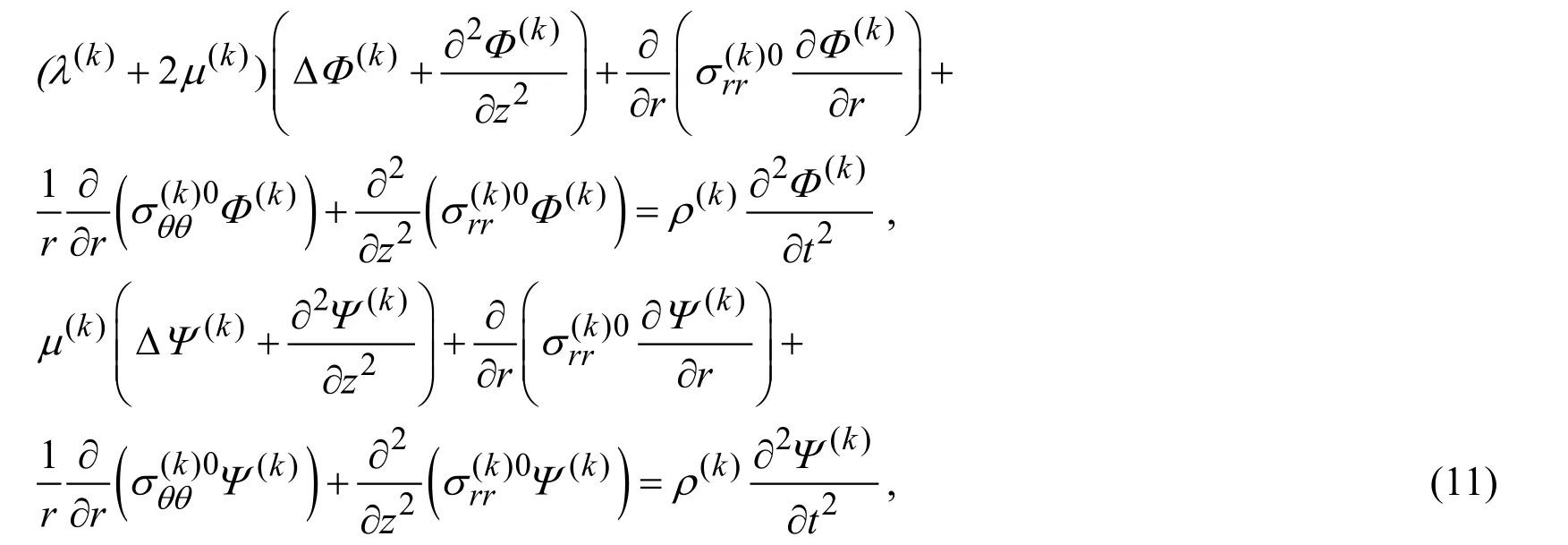
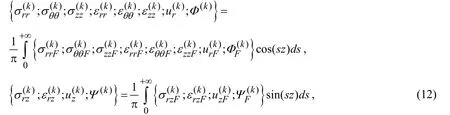
wheresis the Fourier transform parameter and the lower indexFindicates the Fourier transform of the same-named quantities.

Using expressions in (12)the following complete system of equations with respect to the Fourier transforms of the sought values are obtained from Eqs.(3)-(6).

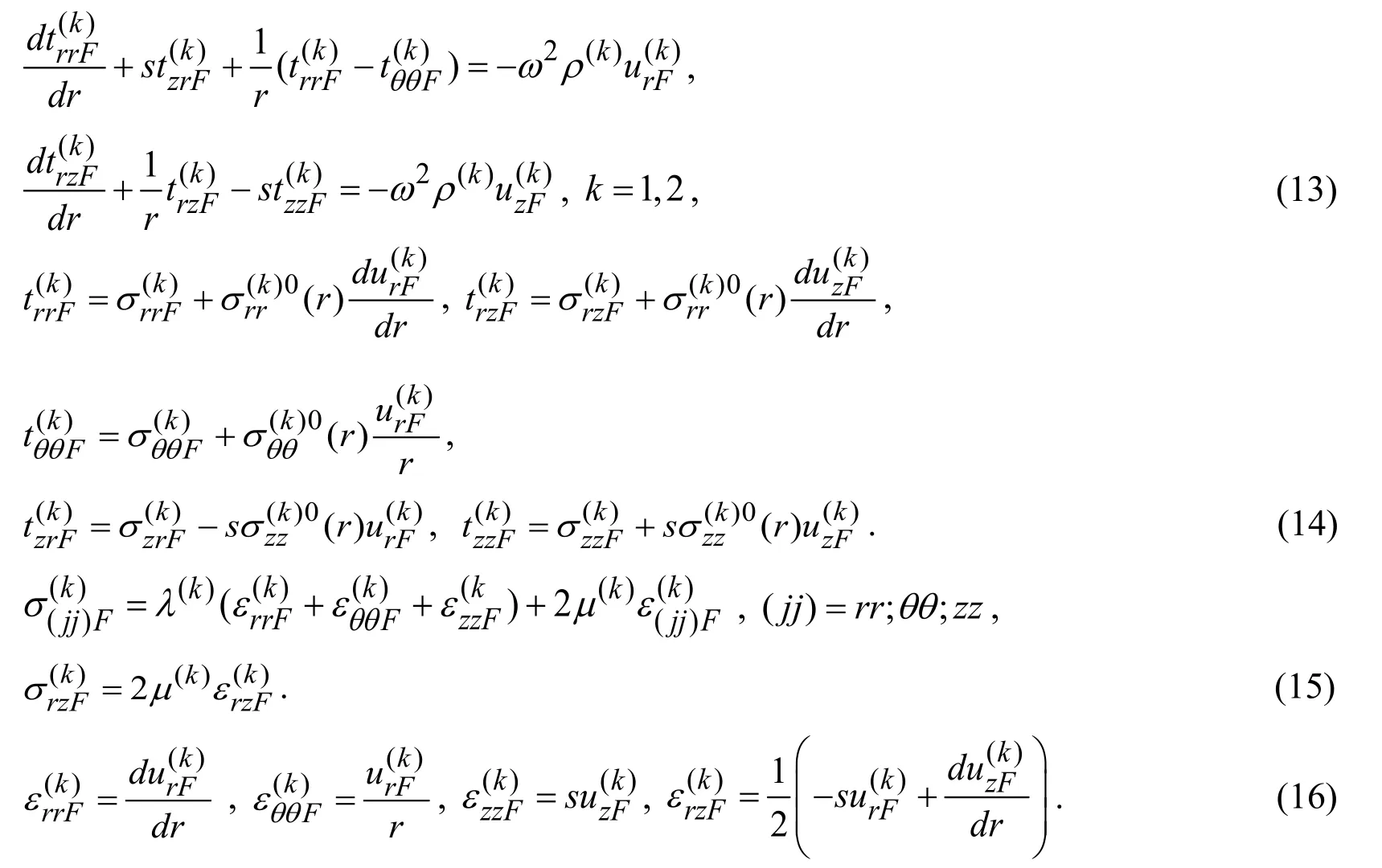
Note that the first boundary condition in (7)is transformed into the following one

however,the second condition in (7)and the contact conditions in (9)remain valid for their Fourier transforms as are.At the same time,the conditions in (8)can be rewritten as

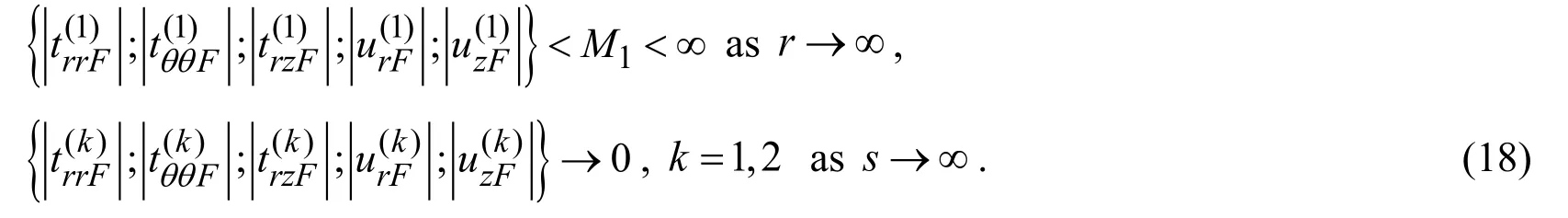
Moreover,substituting the expressions in (12)into the Eqs.(10)and (11)the following equations for the Fourier transforms of the potentialsandare obtained.

In this way,determination of the Fourier transforms of the sought values is reduced to the solution to the equations in (20),for which finding the analytical solution is impossible due to the expressions in (1)and (2).Therefore,we attempt to employ the discrete-analytical solution method for solution to these equations which allows for approximate analytical expressions to be obtained for the Fourier transforms of the sought values.Under application of this method,the solution domain with respect to the radial coordinateris divided into a certain number of subdomains (sub-cylindrical layers)within each of which the pre-stresses determined through the expressions in (1)and (2)are taken as constants,the values of which are calculated through the expressions (1)and (2)by replacing the variablerwithrm,wherermis the middle radius of the subdomain’s (or sublayer’s)cross section.After this procedure,attempts are made to obtain an analytical solution to the system of Eqs.(13)-(16)in each subdomain separately.

Now we attempt to realize the above-described procedure step by step.

3.2 Dividing regions into sub-regions and corresponding contact conditions

According to the foregoing discussions,the region [R-h,R] which occupied the hollow cylinder is divided into thenumber of sub-regions,wheren2= 1,2,...,N2.As well,the region [R,∞] occupied by the surrounding elastic medium is divided into theN1number of finite sub-regions [(R+ (RM-R)(n1- 1)/N1),(R+ (RM-R)n1/N1)] and an infinite sub-region [RM,∞],wheren1= 1,2,...,N1and the numbersN2,N1and the value forRMare determined in the solution procedure from the convergence requirement of the numerical results.

We assume that the non-homogeneous pre-stresses determined through expressions (1)and (2)can be taken as constant within each sub-region determined above and the values of these constants are determined through the following expressions.

In then2-thsub-region occupied by the hollow cylinder

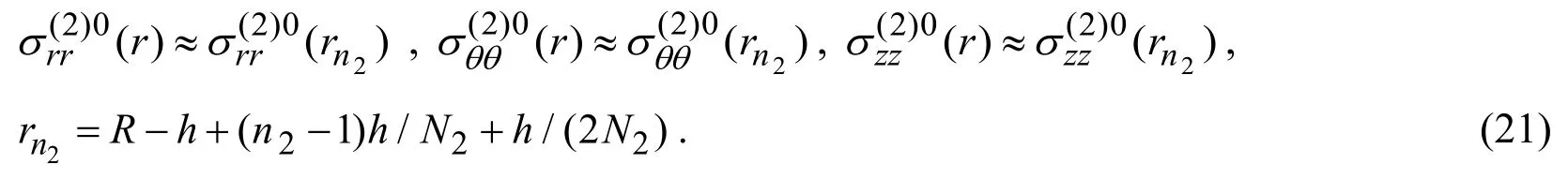
In then1-thfinite sub-region occupied by the surrounding medium

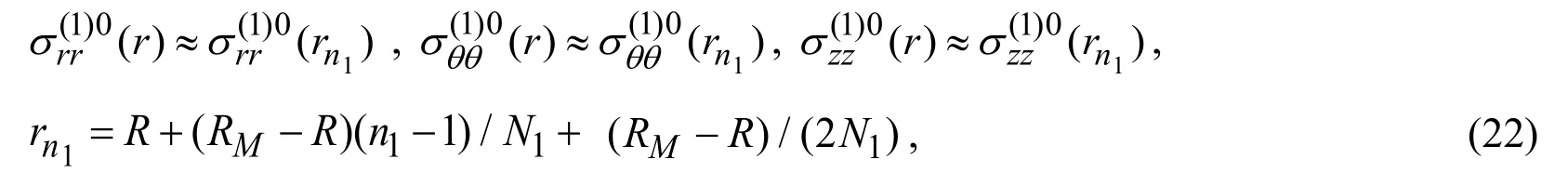
and in the infinite sub-regionalso occupied by the surrounding medium

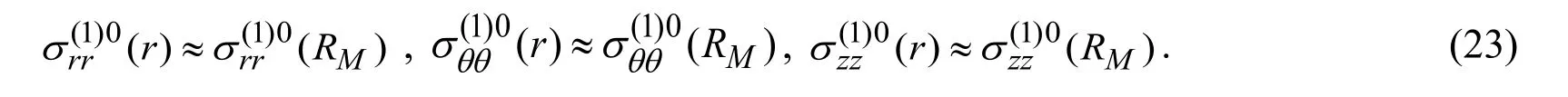
Denoting by the upper index (2)n2(by the upper index (1)n1)the values related to the hollow cylinder (surrounding medium),and by denoting by the upper index (1)∞ the values related to the infinite sub-region,we can write from (7),(9)and (17)the following boundary and contact conditions between the sub-regions.

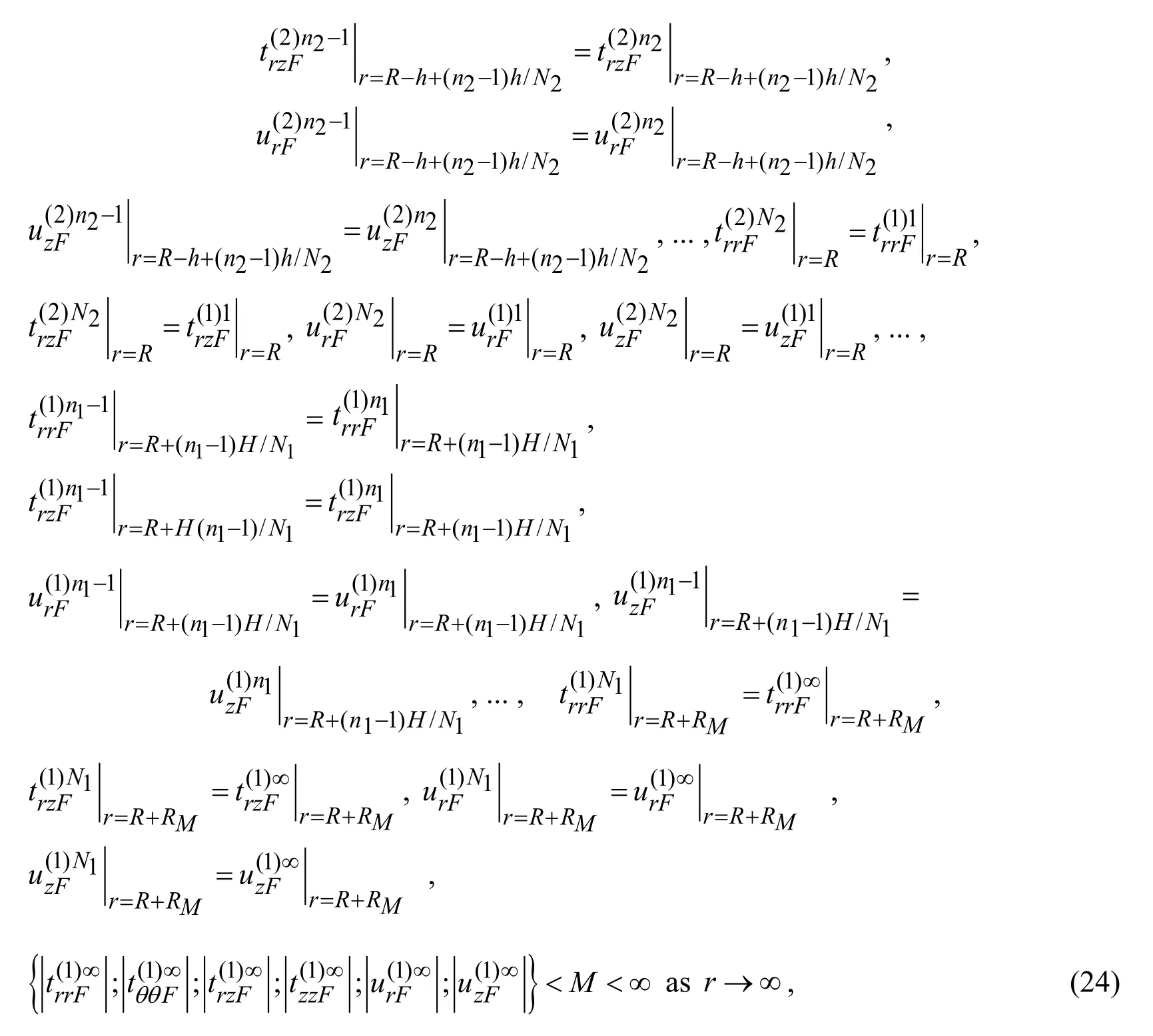
This completes the consideration of the discretization of the solution domain and the formulation of the contact conditions between the subdomains.

3.3 Solution to system of Eqs.(13),(14)and (20)within each subdomain

Under the foregoing discretization procedure,the relations (15),(16)and (19)remain valid in each subdomain as are,and during the mathematical transformations the upper indices (1)n1,(2)n2and (1)∞ must be used instead of the upper indices (1)and (2).

Thus,taking into account (21),(22)and (23),the equations given below are obtained from the Eqs.(13)and (14).

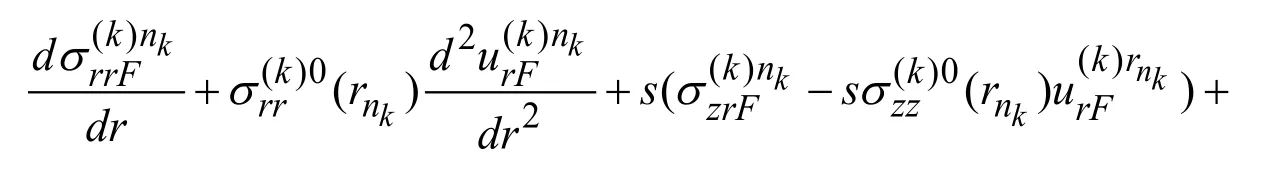
Writing the upper index (1)∞ instead of the upper index (1)niin Eq.(25)we also obtain the corresponding equations for the infinite sub-region

The following equations are also obtained from the equations in (20).

We represent the equations in (26)in the following form

where

3.4 Solution to the equations in (27)

The equations in (27)have the following form

According to Watson [Watson (1966)],using the substitution

we obtain the following Bessel equation for the functiony1(x)from the Eq.(29).

In a similar manner,we can write the following presentation for the potentialsand

and substituting the expressions in (32)into the equations in (27),we obtain the equations

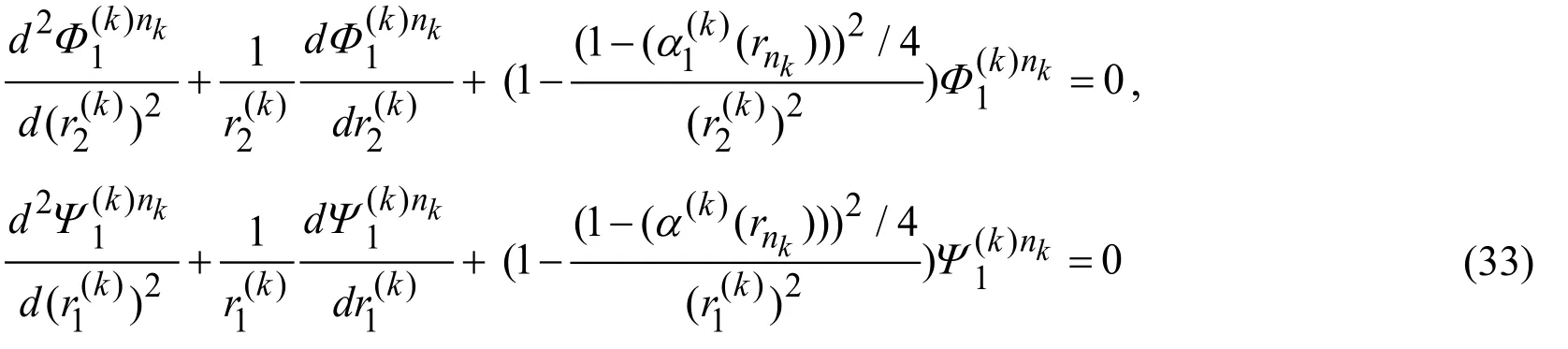
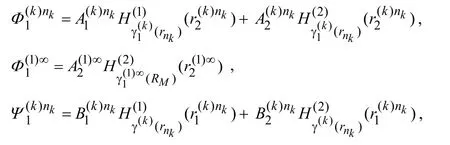
Substituting the expressions in (34)into (32)we obtain:

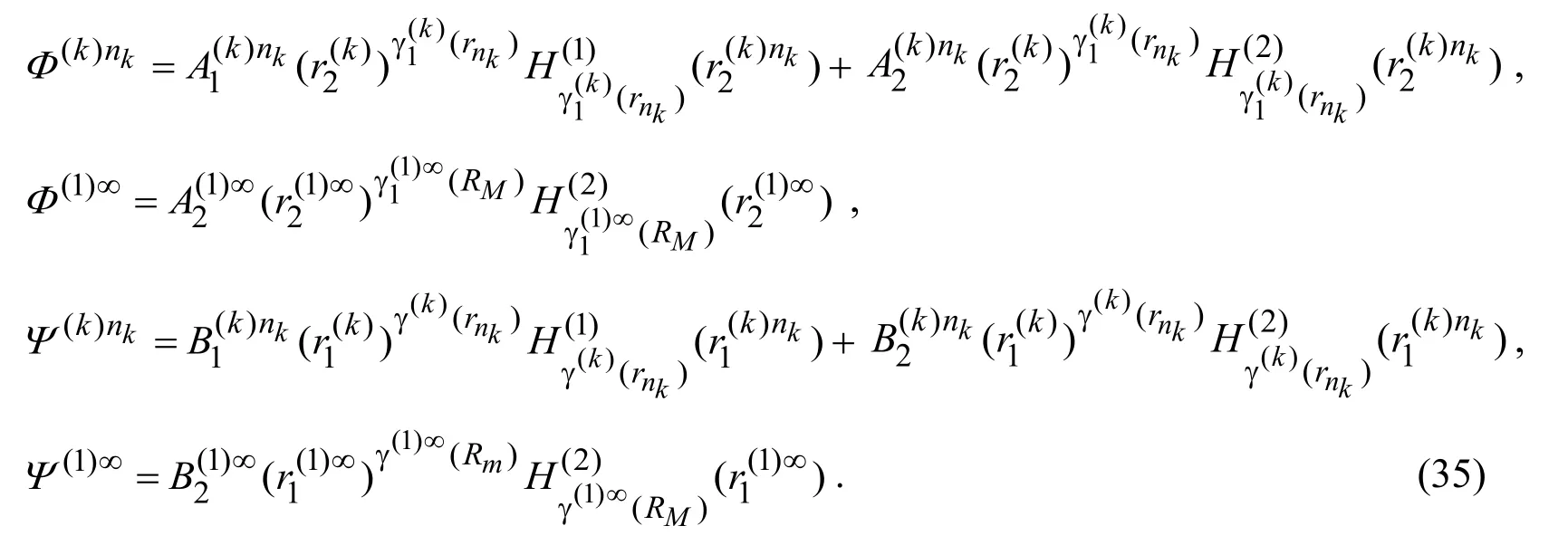
whereandare the Hankel functions of the first and second kind,respectively with the ordera,and

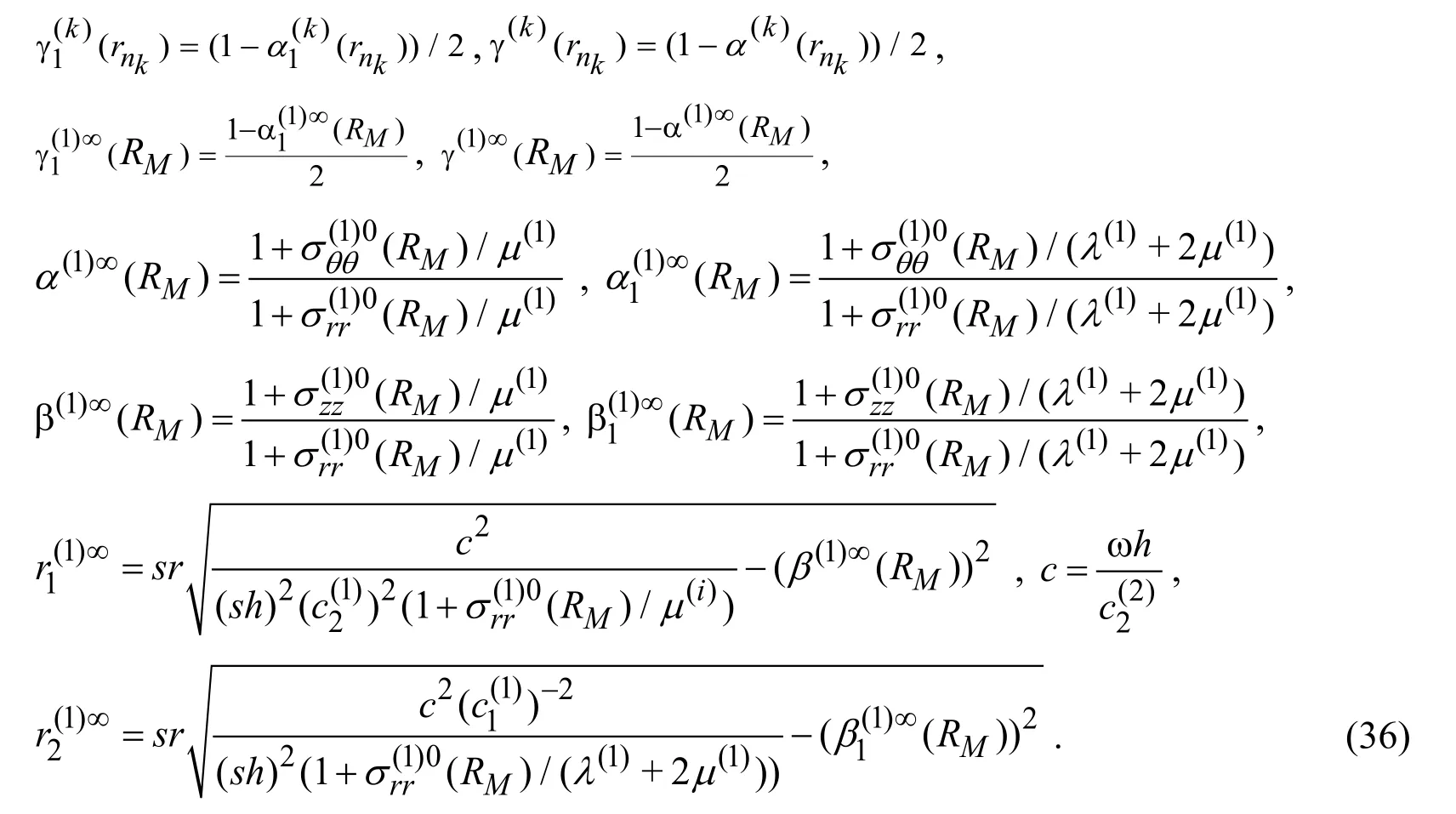
Thus,substituting the expressions in (35)into the expressions in (19)we find the expressions for the Fourier transforms of the displacements which have the following form

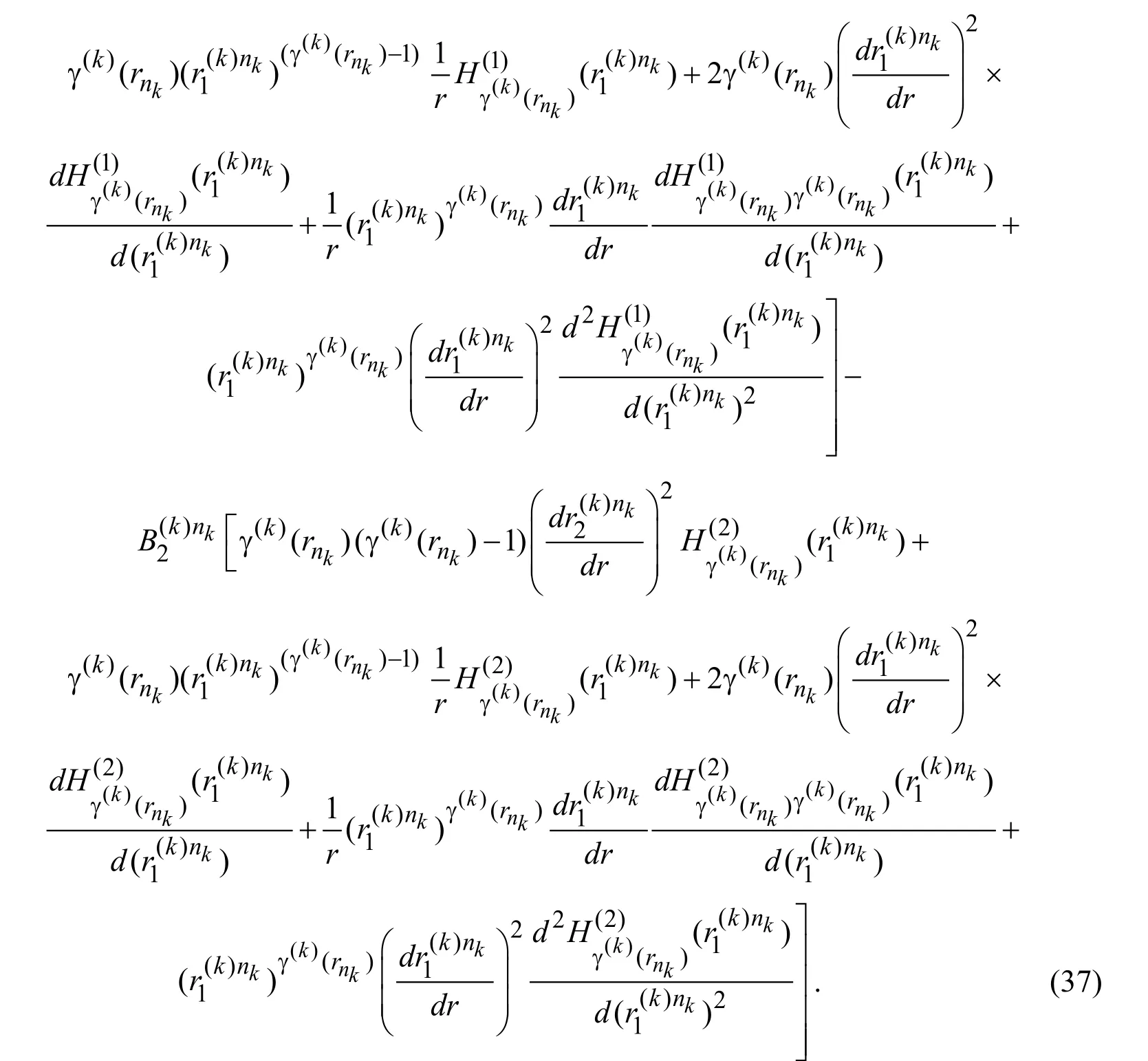
Finally,using expression (37)and Eqs.(15)and (16),we determine the expressions for the Fourier transforms of the stresses.Here,we do not give these expressions in order to reduce the volume of the paper and these expressions can be easily obtained after certain mathematical calculations and transforms.Thus,substituting these expressions into the relations in (24)the system of algebraic equations is obtained for determination of the unknown constants which can be expressed as components of them( = 4(N1+N2)+ 2)dimensional vectorx,where

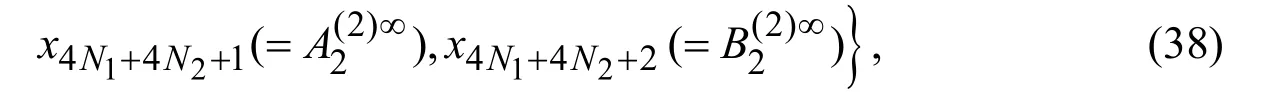
according to which,this system of equations can be presented as follows

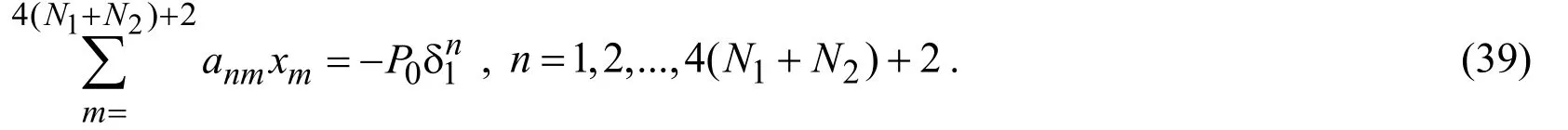
The expressions of the coefficientsnmain (39)can be easily determined from the expressions of the Fourier transforms of the stresses and displacements,the latter of which are given in (37).

In this way,we determine completely the Fourier transforms of the sought values after which their inverses are found through the integrals in (12).The algorithm for calculation of these integrals is developed and applied in the works by Akbarov [Akbarov (2015);Akbarov and Mehdiyev (2017,2018a,2018b,2018c)] and in many others listed therein.According to this algorithm,under the integration procedure,the Sommerfeld contour method is used and the improper integrals are replaced with the corresponding definite integrals,i.e.,the integration intervalis replaced with the finite intervaland this finite interval is divided into a certain number (denote it byNs)of short subintervals in each of which Gauss’s integration algorithm is employed.Under the calculation procedure,it is assumed thatNs= 200 andS1*= 9 which are determined from the convergence requirement of the numerical results.

It should be noted that under the calculation procedure of the Sommerfeld contour method,the Fourier transform parametersis taken as a complex one and is replaced with the complex parameter is+εand,in this way,singularity of the integrated expressions is avoided.Note that,in general,the values of the integrals do not depend on the value of theε,nevertheless,under high frequencies of the external forces it is required to increase the values of theεin order to avoid the jagged configuration of the graphs.Nevertheless,in the present investigation,it is assumed that 0.01=εand,therefore,in some cases,in certain parts of the graphs which will be discussed below,slightly jagged configurations appear.In the cases where the jagged configurations appear to be moderately considerable,the values ofεare increased before 0.02 and in this way,the corresponding graphs are smoothed.

These and other aspects of the algorithm used here are also discussed in detail in the foregoing papers and in the monograph by Akbarov [Akbarov (2015)] and therefore we do not consider here questions related to its validity.

Finally,note that the discrete-analytical solution method which is employed in the present paper was also used in the papers [Akbarov (2006);Akbarov and Panachli (2015);Akbarov,Guliyev and Yahnioglu (2017);Akbarov,Guliyev,Sevdimaliyev et al.(2018)],and is also detailed in the monograph by Akbarov [Akbarov (2015)].Moreover,note that this method was used in the works [Akbarov and Bagirov (2019);Bagirov,Akbarov and Seyfullayev (2018)] in which an attempt is made for consideration of the corresponding wave dispersion and moving load problem acting in the cylindrical cavity containing the infinite elastic medium with non-homogeneous pre-stresses.

In the principal sense,the discrete analytical method employed in the present paper is the same as that employed in the papers [Akbarov,Guliyev,Sevdimaliyev et al.(2018);Akbarov and Bagirov (2019)].However,in the present paper,this method is developed and employed for the problem under consideration,wherein the solution procedure differs significantly from those considered in the previous papers.For instance,the difficulty of the method employed in the present paper is in the use of the Fourier transforms and finding their inverse transform for series problems.At the same time,it should be noted that the difference of the method employed in the present paper from that employed in the papers by Akbarov [Akbarov (2006)] and Akbarov et al.[Akbarov,Guliyev and Yahnioglu (2017)] is that in those papers the discrete analytical method is employed within the framework of the classical linear theory of elastodynamics,however,in the present paper this method (as in the papers by Akbaro et al.[Akbarov,Guliyev,Sevdimaliyev et al.(2018);Akbarov and Bagirov (2019)])is employed within the framework of the threedimensional linearized theory of elastic waves in bodies with initial stresses.Namely,the foregoing statements explain the novelty and originality of the present work in the methodological sense.

Also,note that the discrete analytical solution method applied in the aforementioned and present papers differs from the methods employed in the paper by Wu et al.[Wu,Su,Liu et al.(2018)] and others listed therein,where the axisymmetric longitudinal wave propagation in the pressurized functionally graded elastomeric hollow cylinder is investigated.Under this investigation,the pre-stresses in the cylinder are determined through the solution obtained in the papers [Batra and Bahrami (2009);Chen,Liu and Kitipornchai (2017)] and the solution of the wave propagation equations is solved by employing the state-space formalism for these equations with the approximate laminate or multi-layer technique.Note that in employing the multi-layer technique,not only the values of the pre-stresses in each sub layer,but also the values of the other variable coefficients are taken as constants.However,in the present method,only the values of the initial stresses are taken as the corresponding constants within each sub layer.

This completes the consideration of the solution method.

4 Numerical results and discussions

4.1 Analyses of the numerical results related to the frequency responses of the interface stresses

Now we consider the numerical results which are obtained with employing the method described in the previous section and first we analyze the influence of the inhomogeneous initial stresses on the frequency response of the interface normal stress.Note that under this consideration the magnitude of the initial stresses will be estimated through the ratioq/µ(1).Moreover,note that all the results which will be discussed below are obtained in the case whereN1= 15,N2= 130 andRM/R= 3,the validity of which will be illustrated through the convergence of the numerical results.

Under numerical investigation we consider the following four cases

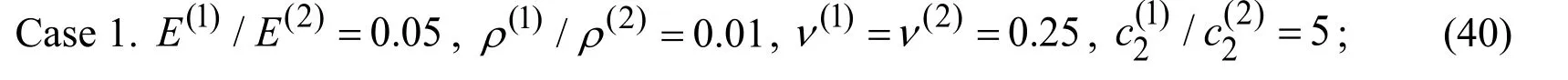
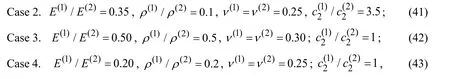
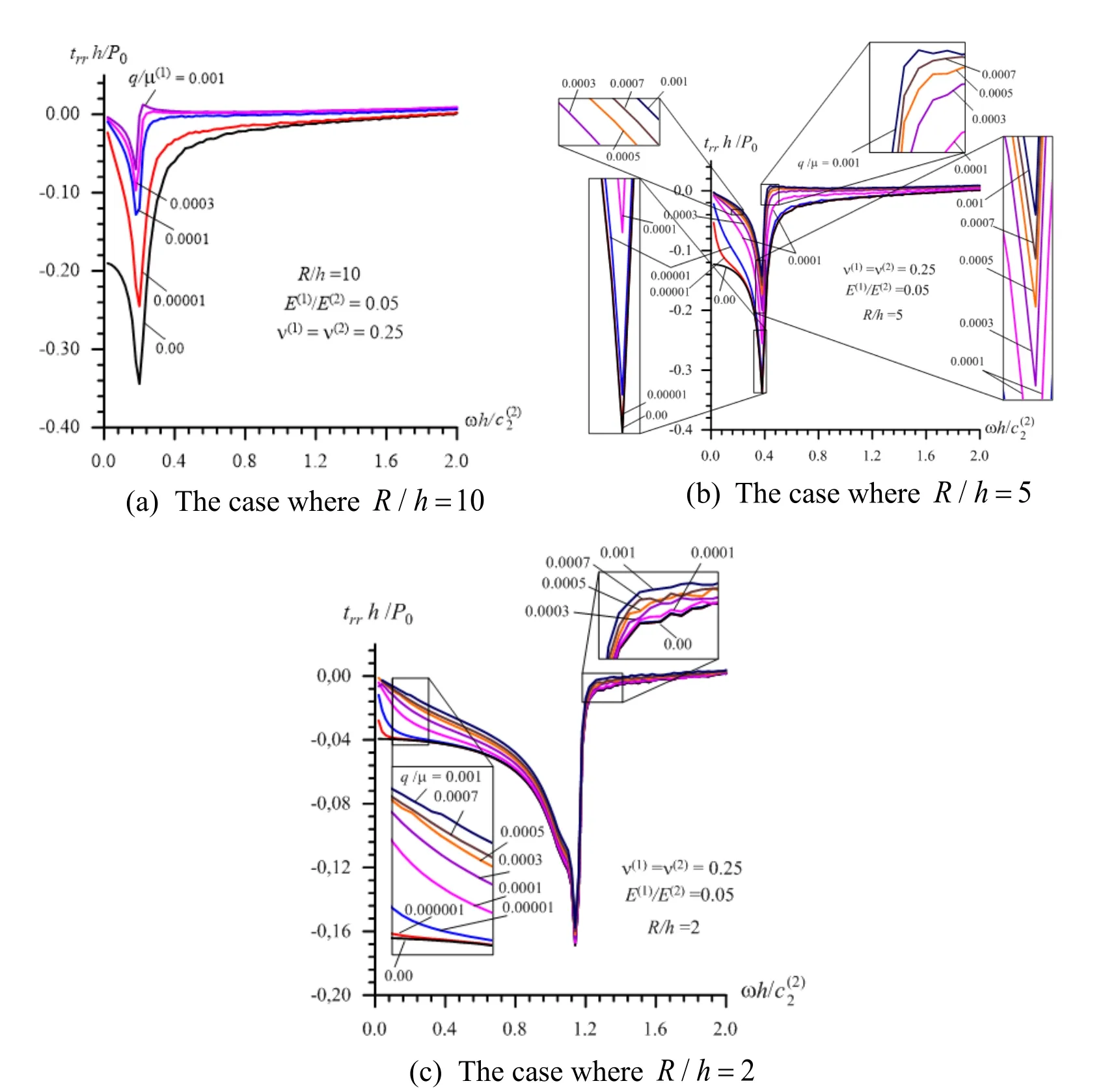
Figure 2:The influence of the initial stresses on the frequency response of the interface normal stress in Case 1 (40)

Consider the graphs related to the frequency response of the interface normal stress

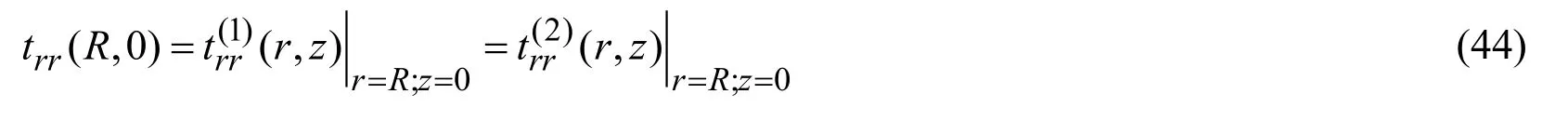
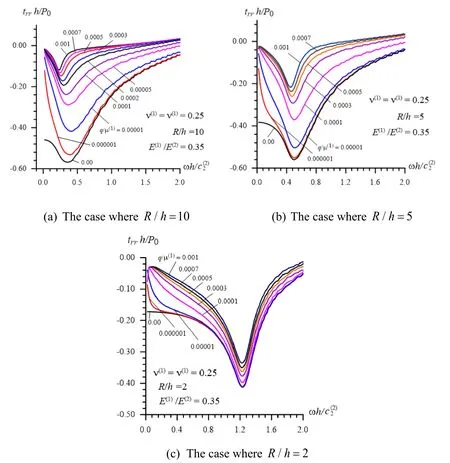
Figure 3:The influence of the initial stresses on the frequency response of the interface normal stress in Case 2 (41)

which are presented in Figs.2,3,4 and 5 for Case 1,Case 2,Case 3 and Case 4,respectively.In these figures,the graphs grouped by the letters a,b and c relate to the cases whereR/h= 10,5 and 2,respectively.Note that the graphs obtained in the case whereq/µ(1)=0 and shown in these figures coincide with the corresponding ones given in the paper by Akbarov et al.[Akbarov and Mehdiyev (2017)].Consequently,the results obtained in the paper by Akbarov et al.[Akbarov and Mehdiyev (2017)] is the particular case of those obtained in the present paper and the originality of the present results is in taking into consideration the influence of the non-homogeneous pre-stresses on the frequency response of the studied quantities.Namely,this constitutes the originality of the obtained numerical results.

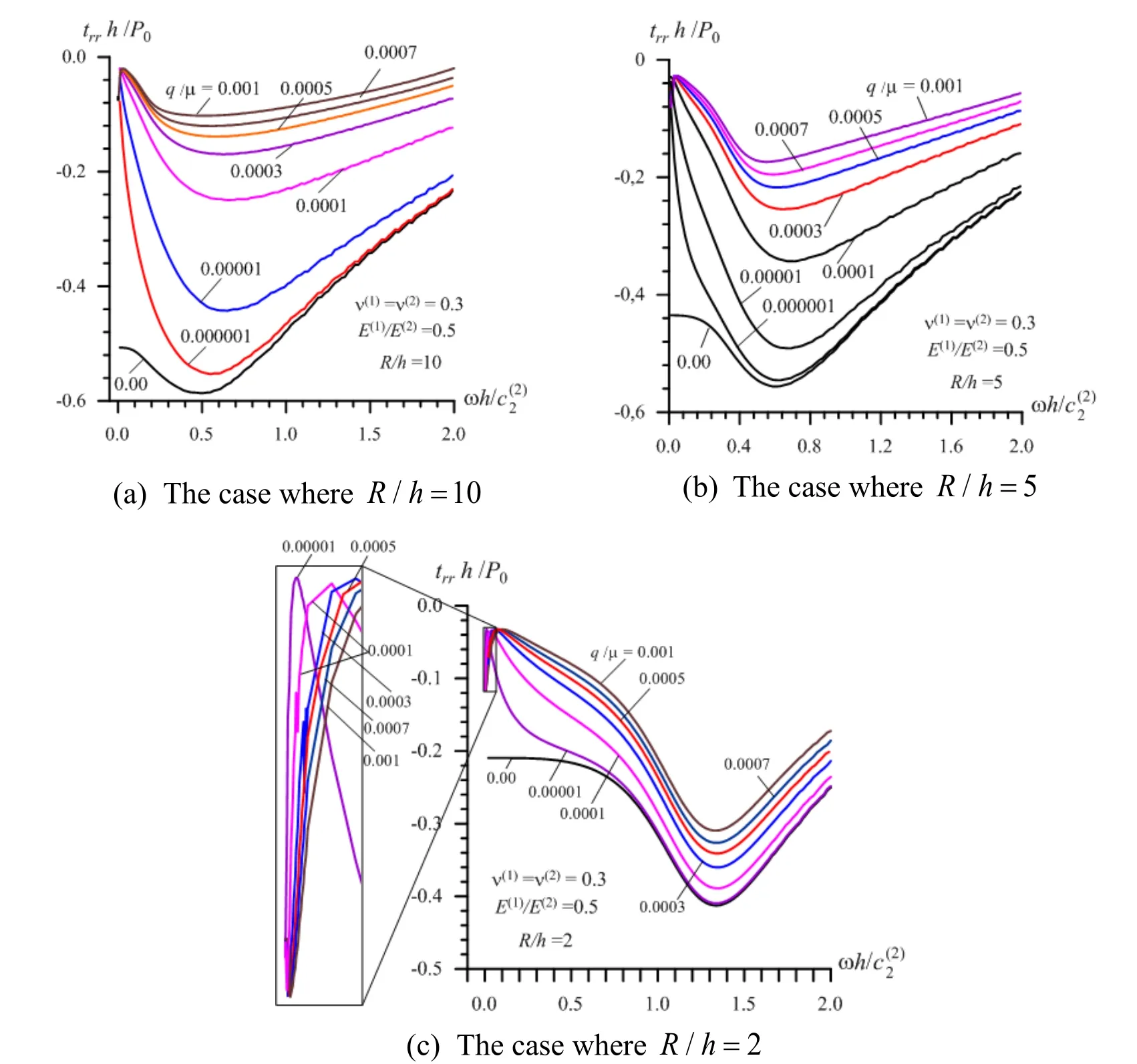
Figure 4:The influence of the initial stresses on the frequency response of the interface normal stress in Case 3 (42)

Unfortunately,we cannot find any results by other authors which can be used for comparison with the present results.Also,we cannot compare the present results with the corresponding ones obtained in the paper by Akbarov et al.[Akbarov and Mehdiyev (2018b)] because in that paper,the corresponding 3D problem is studied within the framework of classical linear elastodynamics.Therefore,for confirmation of the validity of the used calculation algorithm and PC programs,use is made of the results obtained in the paper by Akbarov et al.[Akbarov and Mehdiyev (2017)] and with physico-mechanical considerations.These considerations will be indicated below under discussions of the corresponding numerical results.

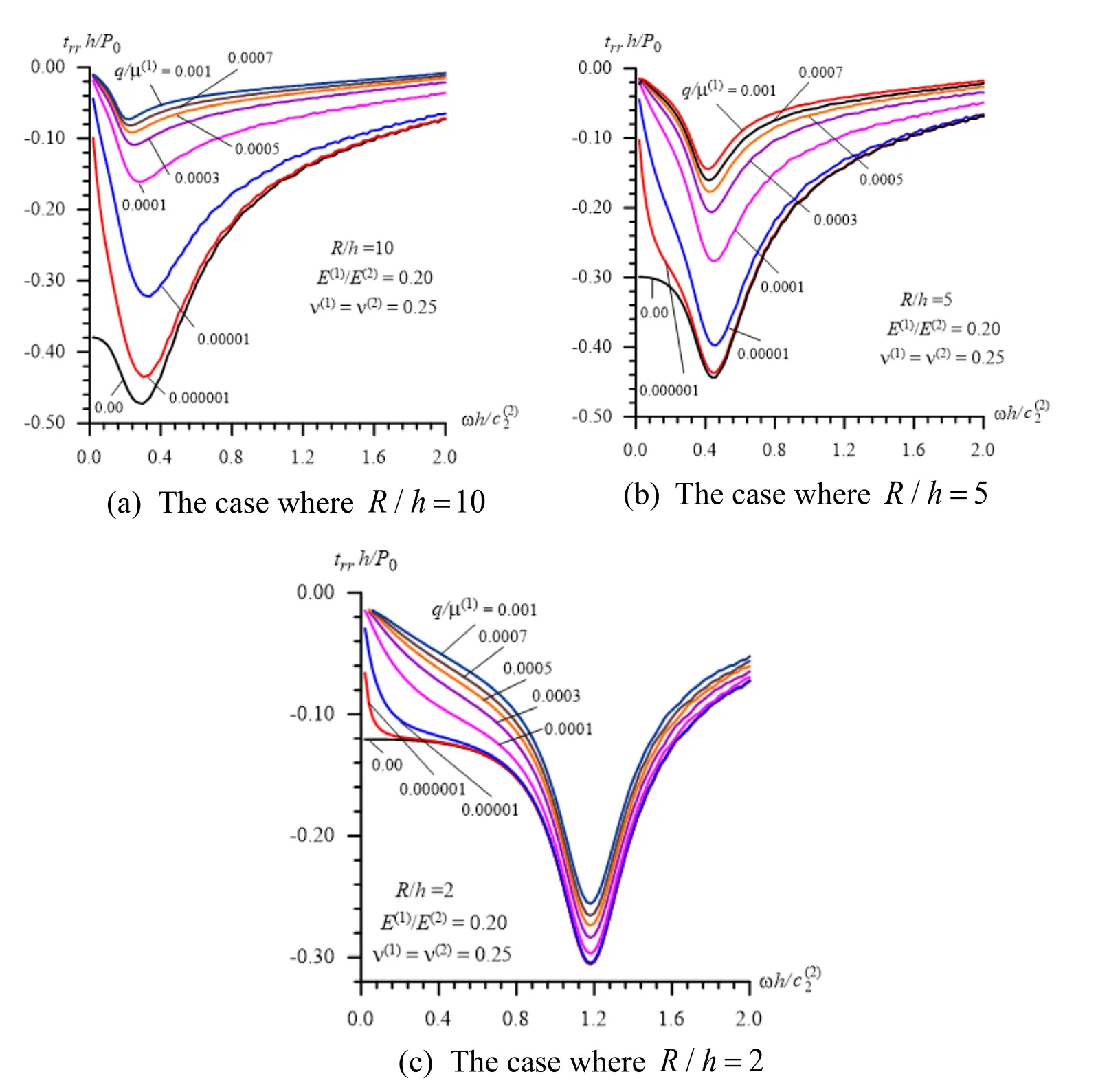
Figure 5:The influence of the initial stresses on the frequency response of the interface normal stress in Case 4 (43)

Thus,we analyze the obtained numerical results and begin this analysis by recalling the character of the frequency response of the quantities related to the forced vibration of the half-space (see,for instance,the works [Lamb (1904);Gladwell (1968);Johnson (1985)])and of the stratified half-space (see,for instance,the corresponding problems detailed in the monograph by Akbarov [Akbarov (2015)] and in others listed therein),and finally,of the system consisting of the hollow cylinder and surrounding elastic medium without any initial stresses (see,the paper by Akbarov et al.[Akbarov and Mehdiyev (2017)]).In these investigations,it was established that the frequency responses have non-monotonic character,i.e.,there exists such a value of the frequency of the forced vibration (we call this value of the frequency as “the resonance frequency”)under which the absolute values of the related quantities have their absolute maximum (we call this value as “the resonance value”).Based on this consideration,according to the results given in Figs.2-5,it can be concluded that this character of the frequency response of the interface normal stress holds also for the case where there exist non-homogeneous pre-stresses determined by the expressions in (1)and (2)in the system under consideration.In toto,the considered type of initial stresses,i.e.,the initial stresses caused by the compressional forces acting at infinity in the radial inward direction,in all cases indicated in (40)-(43),cause to decrease the absolute values of the initial interface normal stress.Note that the magnitude of this decreasing,as well as the magnitude of the decreasing of the “resonance values” of the stress,increases monotonically with the absolute values ofq/µ(1).However,according to the results given in Figs.2-5,the change of the “resonance” frequencies withq/µ(1)is insignificant.Also,it follows from the results given in Figs.2-5,i.e.,from comparison of the results grouped by the letters a,b and c with each other,that the magnitude of the influence of the initial stresses,i.e.,ofq/µ(1)on the absolute values of the stress under consideration increases with the ratioR/h.

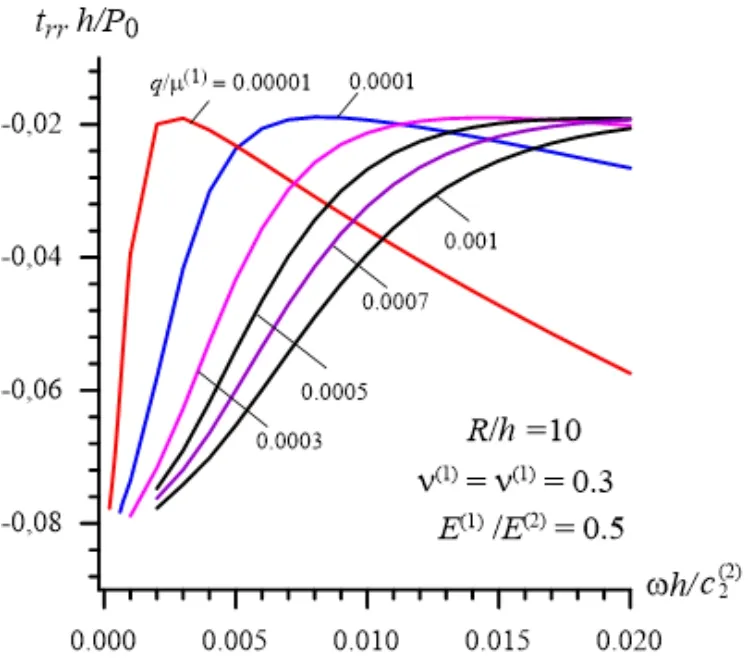
Figure 6:The character of the frequency response of the interface normal stress in the lower frequencies of the vibration of the external forces in Case 3 (42)under R / h= 10

Note that all the conclusions made above on the character of the influence of the prestresses determined with the expressions in (1)and (2),on the character of the frequency response of the interface normal stress agree well with physico-mechanical considerations and this agreement can also be taken as validation of the solution method,the calculation algorithm and the PC programs.

Now,we analyze the influence of the frequency of the vibration on the magnitude of the influence of the initial stresses on the absolute values of the studied interface stress.Moreover,we analyze how the graphs constructed for the cases whereq/µ(1)≠0 approach the corresponding ones constructed underq/µ(1)=0 asq/µ(1)→0.

It follows from the graphs given in Figs.2-5 and from other numerical results,an example of which will be given below,that in the cases where 0.02 ≤≤2.0,a decrease (an increase)in the values of the vibration frequency causes to increase (to decrease)the magnitude of the influence of the initial stresses on the absolute values of the studied stress.Consequently,in low-frequency vibrations,the influence of the initial stresses on the values of the interface stress is more considerable than in the high-frequency cases.Moreover,under high-frequency vibrations,the results obtained for the pre-stressed cases approach the corresponding ones obtained for the case where the pre-stresses in the system are absent asq/µ(1)→0.However,this situation does not take place under lowfrequency vibrations of the system,i.e.,in the cases whereω→ 0.This is because the case whereω→ 0 means the corresponding static additional loading case of the system,for which the results are obtained for the pre-stressed and non-pre-stressed cases,differ from each other.

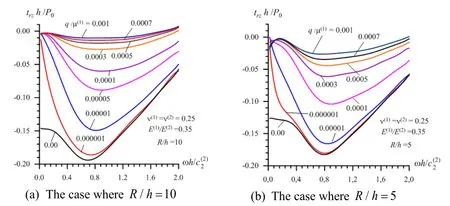
Figure 7:The influence of the initial stresses on the frequency response of the interface shear stress in Case 2 (41)

At the same time,the numerical results show that in the cases whereω→ 0 the character of the dependence between the interface stress and frequency becomes more complicated.As an example,Fig.6 shows the frequency response of the stress in the cases where 0.0001 ≤≤0.02 in Case 3 underR/h= 10,according to which before a certain value of the vibration frequency (denote it by∈(0.0001,0.02)),the absolute values of the stress decrease and after this value the absolute values of the stress increase with the frequency.In toto,the values ofdepend on,andincreases withq/µ(1).Note that the frequency response of the stress in the cases where 0.0001 ≤ωh/ c2(2)≤0.02 is also indicated in the zoomed part in Fig.4(c)which also relates to Case 3 forR/h= 2.

The foregoing particularities of the influence of the inhomogeneous initial stresses on the frequency response of the interface normal stress hold also (in the qualitative sense)for the interface shear stress

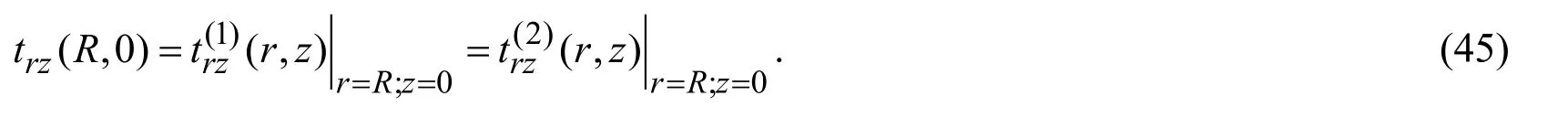
This conclusion can be validated with the graphs shown in Fig.7 which show the frequency response of the interface shear stresstrz(45)in Case 2 underR/h= 10(Fig.7(a))and 5 (Fig.7(b)).It follows from comparison of the results given in Fig.7 with the corresponding ones given in Fig.3 that the magnitude of the interface normal stress is significantly greater than the corresponding ones of the interface shear stress.Note that under construction of the graphs given in Fig.7 the smoothing procedure indicated in Subsection 3.4 is used.

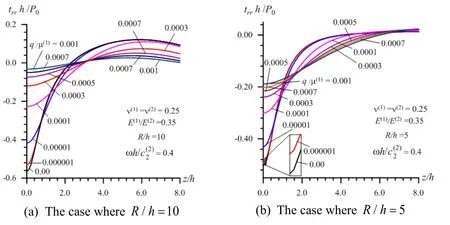
Figure 8:The influence of the initial stresses on the distribution of the interface normal stress with respect to the dimensionless axial coordinate /z h in Case 2 (41)

Now we consider the results which illustrate the influence of the non-homogeneous prestresses on the distribution of the interface stresses with respect to the axial coordinatez/h.For this purpose,we consider the graphs given in Figs.8 and 9 which illustrate the distribution for the interface normal and shear stresses,respectively for Case 2 and the graphs in these figures are grouped by the letter a and b corresponding to the cases whereR/h= 10 and 5,respectively.It follows from these results that all the pre-stresses determined through the expressions in (1)and (2)cause to decrease the absolute maximums of these stresses with respect to the dimensionless coordinatez/h.Moreover,these results show that they have the “vibrational” character and “amplitudes” of this “vibration” are decay with the distance from the point at which the time-harmonic ring load acts.

Figure 9:The influence of the initial stresses on the distribution of the interface shear stress with respect to the dimensionless axial coordinate z /h in Case 2 (41)

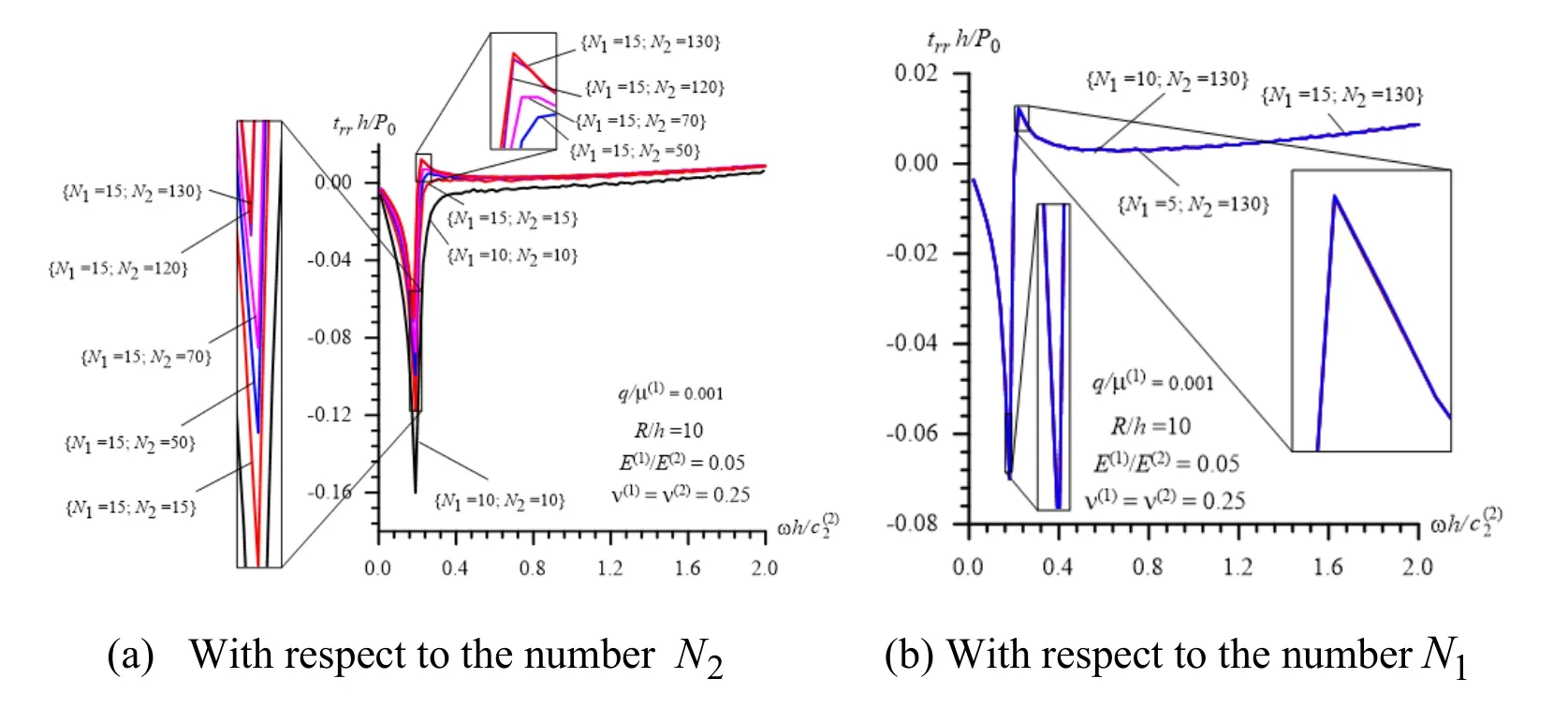
Figure 10:Convergence of the numerical results with respect to the numbers N 2and N1 in Case 1 (40)under R / h= 10

4.2 Numerical results illustrating the convergence of these results

The convergence of the numerical results are controlled through the convergence of the results with respect to the numbersN1andN2,as well as,with respect to the ratioRM/R.For examination of these convergences we consider Case 1 and Case 2 underq/µ(1)=0.001 andR/h= 10 which are the most adverse cases.

Consider the graphs given in Figs.10 and 11 which are constructed for Case 1 (Fig.10)and Case 2 (Fig.11)under various values of the numberN2(graphs grouped by the letter a)andN1(graphs grouped by the letter b)and by the ratioRM/R(graphs grouped by the letter c in Fig.11).It follows from these results that the main parameter which determines the convergence of the numerical results is the numberN2and an increase in the results of this number causes a decrease of the absolute values of the interface stresses.Comparison of the results obtained in the cases whereN2= 120 andN2= 130 coincide with each other with the accuracy 10- 6.Therefore,all the results discussed in the previous subsection are obtained in the case whereN2= 130 and here it is assumed thatN1= 15 andRM/R= 3,the selection of which is based on the results given in Fig.10(b),Fig.11(b)and Fig.11(c).Note that under construction of the graphs given in Fig.11(a)the smoothing procedure indicated in Subsection 3.4 is used.

Figure 11:Convergence of the numerical results with respect to the numbers N 2 (a)and N1 (b)and to the ratio RM /R (c)in Case 2 (41)under R / h= 10

4.3 Notes on the application of the obtained theoretical results

Now we attempt to argue the possible real applications of the obtained results,despite the difficulty of this realization,of the axisymmetric time-harmonic ring load which acts in the interior of the cylinder.Nevertheless,the theoretical results obtained within this assumption can provide very important information on the considered type of non-linear dynamical effects such as the influence of the inhomogeneous initial stresses on the forced vibration of the system under consideration.For instance,the results obtained on the influence of the inhomogeneous initial stresses on the amplitudes of the interface stresses caused by additional time-harmonic loading hold in the qualitative sense also for nonaxisymmetric additional time harmonic loading cases.Moreover,the theoretical results on the dependence of the aforementioned non-linear effects on the mechanical and geometrical properties of the system are valid also in the qualitative sense in nonaxisymmetric time-harmonic loading cases.

The solution method developed and the results obtained in the present paper can also be used in the following applications.We recall that in the present paper the steady-state axisymmetric dynamic problem has been considered,according to which,if using the solution procedure of this problem whereiωis taken as the Laplace transformation parameterp,then the theoretical results obtained in the present paper in the cases wherep→ 0 andp→∞ can be taken with a certain accuracy as the results related to the corresponding non steady-state dynamic problem with zero initial conditions undert→∞ andt→ 0,respectively.An example of such a non-steady state dynamic problem is an explosion inside the pipes used in geological prospecting.Consequently,the theoretical results obtained in the present paper may have applications not only in the qualitative sense,but may also have direct quantitative applications for the limit cases of the corresponding non stationary non-linear dynamical problems.

5 Conclusions

Thus,in the present paper within the scope of the 3D linearized equations and relations of the theory of elastic waves in pre-stressed bodies,the forced vibration of the initially inhomogeneous stressed cylinder surrounded with an initially inhomogeneous stressed medium under action of the time-harmonic ring load,is studied.This study is made for the axially symmetric case by employing the so-called discrete analytical method which allows us to find the approximate analytical solution to the corresponding boundary value problems.It is assumed that the initial inhomogeneous stresses appear as a result of the uniformly distributed compressional normal forces acting at infinity in the radial inward direction.The aim of the investigations is to determine how the initial stresses influence the stress state in the system as a result of the action of the additional dynamic timeharmonic ring load.This influence appears as a result of the non-linear effect which is described through the linearized theory of elastic waves in initially stressed bodies,the equations and relations of which are obtained from the corresponding geometrical nonlinear dynamic equations and relations of the theory of elastodynamics through the linearization procedure.

Numerical results on the influence of the initial stresses on the frequency responses of the interface stresses are presented and discussed.Under these discussions,the magnitude of the non-homogeneous pre-stresses is estimated through the ratioq/µ(1)whereqis the intensity of the initial forces acting at infinity in the inward radial direction andµ(1)is the shear modulus of the surrounding medium.The analyses of the numerical results allow us to draw the following concrete conclusions on the character of the influence of the aforementioned initial stresses on the frequency responses of the interface stresses caused by the additional time-harmonic ring load acting in the interior of the cylinder.

- The non-homogeneous pre-stresses appearing as a result of the initial compressional forces mentioned above cause to decrease the absolute values of the interface stresses and this character of the influence of the pre-stresses is in good agreement with well-known physico-mechanical and engineering considerations;

- The phenomenon described in the previous conclusion can be modelled only within the scope of the geometrically non-linear theories of deformable bodies,the first iteration for which is the so-called 3D linearized theory of elastic waves in pre-stressed bodies;

- The frequency responses of the interface stresses have non-monotonic character for all the considered values of the initial loading,i.e.for all the values of the ratioq/µ(1);

- An increase in the absolute values of the ratioq/µ(1)causes a decrease in the “resonance” values of the interface stresses and the magnitude of this decrease grows monotonically withq/µ(1);

- The dependence of the “resonance” frequencies on the ratioq/µ(1)is insignificant,however,these frequencies increase with the ratioR/h,wherehis the thickness andRis the external radius of the cross section of the cylinder;

- An increase in the values of the ratioR/hcauses to increase the magnitude of the influence of the initial stresses on the absolute values of the interface stresses;

- The comparison of the numerical results obtained in the cases indicated in (40)-(43)and illustrated in Figs.2-5 shows that the absolute values of the “resonance” stresses with respect to the elasticity constants of the materials of the constituents of the system are determined not only with the ratiobut also with the ratio,so that the absolute values of the “resonance” stresses increase with decreasing of the ratio(as in Case 1 (40),Case 2 (41)and Case 3 (42)),however,in the cases where the ratioremains constant (as in Case 3 (42)and Case 4 (43))then the magnitude of the absolute values of the “resonance” stresses is determined with the ratioaccording to which,an increase in the values of the ratiocauses to increase the absolute values of the “resonance” stresses;

- A decrease of the frequency of the additional external ring load causes to increase the influence of the initial stresses on the values of the interface stresses,however,the magnitude of this influence decreases with increasing of the noted frequency.

Besides all of the foregoing conclusions,other concrete conclusions can also be made following on from the numerical results given in Figs.6-11 which can be easily made by prepared readers.