Finite Element Investigation of Flow Field Below Asymmetric Drill Bits for Reverse Circulation in Drilling Tight Oil and Gas Reservoirs

YiLuo,ErxiuShi,YinFeng,BoyunGuoandLiehuiZhang

Abstract: Development of unconventional tight oil and gas reservoirs such as shale pays presents a huge challenge to the petroleum industry due to the naturally low permeability of shale formations and thus low productivity of oil and gas wells.Shale formations are also vulnerable to the contamination of the water in the drilling and completion fluids,which further reduces reservoir permeability.Although gas-drilling (drilling with gas)has been used to address the issue,several problems such as formation water influx,wellbore collapse,excessive gas volume requirement and hole cleaning in horizontal drilling,still hinder its application.A new technique called gas-lift drilling has recently been proposed to solve these problems,but the optimal design of drilling operation requires a thorough investigation of fluid flow field below the asymmetric drill bits for evaluating the fluid power needed to clean the bottom hole.Such an investigation is conducted in this work based on the Finite Element Method (FEM)implemented in an open source computational framework,FEniCS.Pressure and flow velocity fields were computed for three designs of drill bit face characterized by radial bit blades and one eccentric orifice of discharge.One of the designs is found superior over the other two because it generates relatively uniform flow velocities between blades and provides a balanced fluid power needed to clean all the bit teeth on each bit blade.To quantify the capability of borehole cleanup presented by three drill bit designs,the energy per unit volume is calculated in each region of drill bit and compared with the required value suggested by the literature.In addition,the developed FEM model under FEniCS framework provides engineers an accurate tool for optimizing drill bit design for efficiently gas-lift drilling unconventional tight oil and gas reservoirs.

Keywords: Gas-lift drilling,reverse circulation,unconventional reservoirs,bit design.

1 Introduction

Tight oil and gas reservoirs are generally regarded as oil reservoirs with permeability less than 1 mD and gas reservoirs with permeability less than 0.01mD.Tight sands and shale oil/gas reservoirs are examples.The oil and gas industry face a huge challenge in producing oil and gas from the tight oil and gas reservoirs due to the low-permeability-controlled low productivity of wells.The low conductivity of wells is attributed not only to the natural low permeability of reservoir rocks but also the permeability damage by the water from the drilling and fracturing fluids.According to Li et al.[Li,Guo,Gao et al.(2012)] the productivity of wells can drop easily by 50% in hydraulically fractured wells due to water filtration,in addition to the permeability damage due to capillary pressure which is still a major factor dominating well productivity [Romero,Valko and Economides (2003)].

Non-aqueous fracturing has been tested for reducing permeability damage and thus improving oil and gas well productivity in unconventional reservoirs [Guo,Shan and Feng (2014)],and gas-drilling (drilling with gas as a circulation fluid)has proved to be more promising to resolve the issue of permeability damage [Li,Guo,Yang et al.(2014)].Although many researches on gas-drilling [Moore and Lafave (1956);Smith,Neufeld and Sorrells (1986);Supon and Adewumi (1991)] has been conducted,there are still several problems that hinder the application of gas-drilling technique.The first problem is the formation fluid (water)influx in drilling wet formation intervals [Lyons,Guo,Graham et al.(2009)],where very high gas injection rates must be used to remove the formation fluid,which is not feasible in many areas.This problem is considered as a bottleneck for the applications of the gas-drilling technique.The second problem is also related to the excessive formation fluid influx.It is the wellbore collapse caused by the wetting of formation rock in the upper-hole sections by the produced formation water.Formation rocks in the upper hole section,such as shale,containing clays,swell and create stresses at the hole-wall,causing borehole collapse [Lyons,Guo and Seidel (2001)].The third problem is the extremely high gas injection rate required for effectively removing drill cuttings in the annulus drilled with large drill bits [Guo and Ghalambor (2002)].The fourth problem is the borehole cleaning issue in horizontal drillings where drill cuttings accumulate and form domes in the horizontal annulus.This can cause high-drag and torque and sometimes operation failure due to pipe sticking [GRI (1997)].

In order to address problems limiting the application of gas-drilling technique,a new gasdrilling technique called gas-lift drilling was proposed by Guo et al.[Guo,Li,Song et al.(2017)] to solve the problems associated with the conventional gas-drilling technique.The gas-lift drilling is designed to use reverse circulation for removing drill cuttings and produced formation water through the inside of the drill string,instead of the annulus.Different from fluid circulation in conventional drillings where drilling fluid enters the borehole system from drilling string,passing through drill bit nozzles,and flows back to surface through annulus,in the reverse circulation,the drilling fluid is pumped into the drilling system from the annulus,and flows back to the wellhead through the drilling string.The reverse circulation presents several advantages over the conventional one,such as reducing the formation leakage,protecting the oil and gas formation,cutting sample very clear [Li,Ru,Li et al.(2006)],critical sampling,lost circulation zones,and economical circulating volumes [Hand,Bishop and Perking (1979)].Reverse circulation also has attractions for the offshore environment [Crabtree,Li and Luft (2007)].When using the conventional circulation drilling technology with symmetric,the formation rock in the center of borehole could be broken by the pressure from water hole,but this mechanism does not work for gas-lift drilling with a reverse circulation.Because in the conventional circulation,drilling fluid enters the borehole system from drilling string,passing through drill bit nozzles,and flows back to surface through annulus,so that the cuttings do not need to pass through drill bit nozzles (nozzle is a device designed to control characteristics of a fluid flow,especially to increase velocity).While for the reverse circulation,drill cuttings need to enter the insider of drill pipe through the orifice (the size of the orifice is larger than nozzle to allow cutting getting through).That means the formation rock right below the orifice cannot be effectively crashed because no blade can reach the center area for a symmetric drill bit where the orifice is located in the center.Therefore,the concept of asymmetric drill bits is proposed for the reverse circulation to allow blade covering center area and improve the drilling efficiency.However,when drilling using an asymmetrical bit,the flow pattern is not uniform for different regions formed by the pattern of blades on a drill bit,so that each region presents different capability in removing formation cuttings.That means,for a symmetric drill bit,the similar flow field is expected in each region between drill bit blades implying the same bole cleanup efficiency.While for an asymmetric drill bit,cuttings may not be effectively removed in a particular region that eventually reduces the overall drilling efficiency.Thus,it is significant to perform a thorough investigation of fluid flow field below the asymmetric drill bits to evaluate the fluid power so as to ensure the power is adequate to clean the borehole in each region between bit blades.

The objective of this paper is to perform a theoretical study for the concept of asymmetric drill bits.To clarify the effect of various bit designs on the borehole cleanup capability,three conceptual designs of asymmetric drill bits are proposed and the fluid flow field below each drill bit is numerically investigated.Researches [Walker and Li (2000);Li and Walker (2001);Yong,Lihong,Deyong et al.(2016);Zhu,Huang,Wang et al.(2015)] have been conducted to evaluate the borehole cleanup,the concept of critical energy per unit volume of fluid s adopted in this study to quantify the borehole cleanup capability,and as suggested by Lyons et al.[Lyons,Guo and Seidel (2001)],to effectively remove drill cuttings,the required energy per unit volume is 143.4 J/m3,which is used to study the applicability of the proposed three drill bit designs.Numerical investigations are conducted using Finite Element Method (FEM).Pressure and flow velocity fields were computed for three designs of drill bit face (referred to as Bit Design I,Bit Design II and Bit Design III)where the first two designs are characterized by four bit blades and one eccentric orifice of discharge while the third one consists of six bit blades and one orifice of discharge.The simulation results reveal that the third design of drilling bits (Bit Design III)is superior over the other two designs because it generates relatively uniform flow velocities between the blades,which provides enough balanced fluid power needed to clean all bit teeth on bit blades.The computational framework,FEniCS,is employed which simplifies the implementation of finite element method and provides engineers an excellent tool for optimizing bit design for efficient gas-lift-drilling in developing unconventional tight oil and gas reservoirs.This research will enhance the understanding about the effect of the drill bit face design on the flow patterns via investigating the flow patterns for the proposed three conceptual designs of asymmetric drill bit.The paper associates the regional flow patterns with the capability of borehole cleanup efficiency in term of the energy per unit volume,and paves the way for the further optimization and application of the asymmetric drill bit in the gas-lift drilling as well as other engineering applications.In addition,the powerful tool,FEniCS,is firstly time introduced into such simulation for assisting the drill bit design.Details regarding the geometric designs and FEM implementation in FEniCS are elaborated in Section 2 and Section 3,respectively.

2 Drill bit face design

Instead of pumping gas down the drill string,through the drill bit and up the annulus to the surface in conventional gas-drilling,the gas-lift-drilling uses reverse circulation of gas,where the gas is pumped to the annulus,through the drill bit,and up the drill string to the surface in the gas-lift-drilling operations.This reverse circulation requires gas to sweep drill cuttings at the bottom hole and entrain them to a large orifice of discharge so that the drill cuttings are pushed to the inside of drill string.This process of gas-cleaning of bottom hole requires the drill bit face designed in such a way that gas flows between blades uniformly to balance the fluid power for sweeping the bottom hole and remove drill cuttings completely.The discharge orifice is off the bit center to cut rock at bit center.Because of this asymmetric nature of bit face,the bit blades must be designed to create balanced fluid velocity and thus cleaning power between the bit blades.The cleaning power is evaluated by the average kinetic energy of gas flow between blades.This evaluation is done on basis of FEM solution to the pressure and velocity fields.

Three asymmetric drill bit face designs are considered in FEM modeling of fluid flow,as demonstrated in Fig.1,where Fig.1(a)shows an original design of the bit face with 4 blades of equal-width and a small fluid exit port.This is a simple design for easy manufacturing.Fig.1(b)presents a modified bit face design with 4 blades of non-equalwidth but a large fluid exit port.This design tests the effects of port size and blade size on the fluid flow field.Fig.1(c)illustrates a bit face design with 6 blades of non-equal-width and a large fluid exit port.This design tests the effects of number of blades and arrangement on the fluid field.All dimensions are measured in millimeters in Fig.(1)but in meters for computational models.The dark areas represent fluid entry and exit sections and the white areas stand for bit blades for installation of bit teeth.The blades are designed to be 25.4 mm (1 inch)high so that the flow domain between bit blades is 25.4 mm (1 inch)thick when the bit teeth touch the bottom hole.

Figure 1:A bit face design (a)with 4 blades of equal-width and a small fluid exit port;(b)with 4 blades of non-equal-width and a large fluid exit port;(c)with 6 blades of non-equalwidth and a large fluid exit port

3 Mathematical model

3.1 Governing equations

The objective of this investigation is to achieve a flow field where the fluid power is balanced among the sections between bit blades so that the drill cuttings between the blades are thoroughly entrained by the flowing fluid.This fluid power is evaluated by the kinetic energy of the fluid.The average fluid velocities between the blades are computed for calculating the kinetic energy.

Assuming negligible density change in the area below the drill bit,the incompressible Navier-Stokes equations can be employed to describe the flow behavior.

where,u and p denote velocity (vector in m/s)and pressure (scalar in Pa),respectively,ρ is the fluid density (kg/m3),σ(u,p)is the stress tensor given as follows for a Newtonian fluid.

where,μis the dynamic viscosity (Pa·s)and ∈(u)is the strain-rate tensor

A major difficulty in solving above equations is the coupling of velocity and pressure fields.Therefore,numerous researches have been performed and various splitting and iterative strategies were studied.The interest in using projection methods to overcome this difficulty in viscous incompressible flows started in the late 1960s with the ground-breaking work of [Chorin (1968);Temam (1969)],which is referred to as Chorin’s method.The most attractive feature of projection methods is that,at each time step,one only needs to solve a sequence of decoupled equations for the velocity and the pressure,making it very efficient for large scale numerical simulations [Guermond,Minev and Shen (2006)].However,these solutions were lack of accuracy until a modified version was presented by Goda [Goda (1979)],known as Incremental Pressure Correction Scheme (IPCS).The IPCS improved the computational accuracy compared to the original scheme and was employed in this study.

The implementation of IPCS scheme involves three steps.Step 1 is to compute a tentative velocity u∗by advancing the momentum equation (Eq.(1))by a midpoint finite difference scheme in time but using the pressure pnfrom the previous time interval.We will also linearize the nonlinear convective term by using the known velocity unfrom the previous time step:un·Δun.The variational problem for this first step is

To derive a weak formulation for Finite Element Method,test functionsvandq,chosen respectively in proper function spaces,are required (note that q is a scalar-valued test function from the pressure space,whereas the test function v is a vector-valued test function from the velocity space).By multiplying Eq.(5)by the test functionvand Eq.(2)by the test functionq,and integrate over the domain Ω,we have,

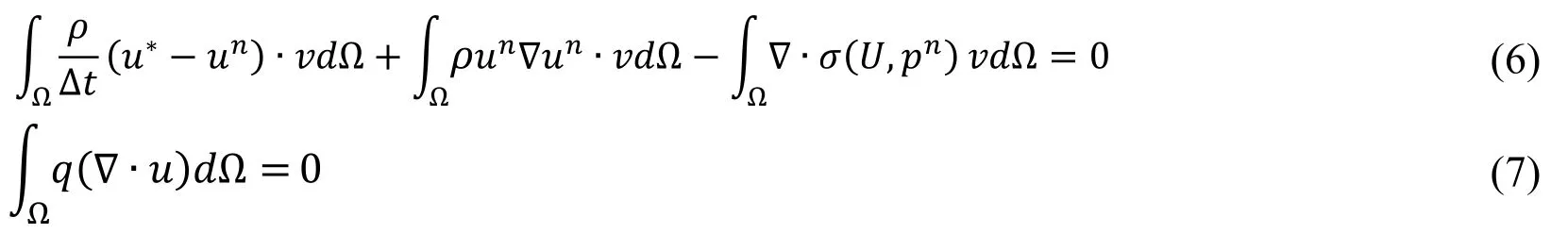
The third term in Eq.(6)can be further derived and yields [Goda (1979)].

The tentative velocity u∗can therefore be determined via solving Eq.(8).

Step 2is a correction to update the pressure field (pn+1)from the resultant tentative velocity via solving Eq.(10)that is obtained by combining Eq.(9)and Eq.(7).

where the boundary terms have been eliminated [Langtangen and Logg (2017)].

Step 3is to update the velocity.This step can be accomplished through Eq.(11)(weak formulation of Eq.(9))based on the tentative velocity u∗and the pressure pn+1calculated from Step 1 and Step 2,respectively.

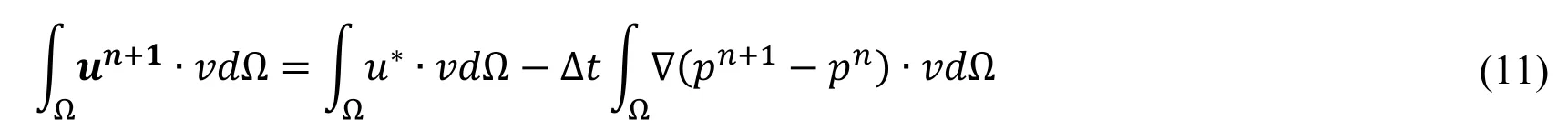
In summary,we may thus solve the Navier-Stokes equations efficiently by solving a sequence of three linear variational problems in each timestep.

The IPCS scheme was implemented in FEniCS (https://fenicsproject.org/),an open-source computing platform for solving partial differential equations (PDEs)based on FEM [Braess (2007);Brenner and Scott (2008)].In FEniCS code,previous three steps are addressed sequentially,and each step consist of three operations.The first operation is to translate the equation in each step into the variational format.This procedure is shown in Fig.2(a)where,code below comments “# Define variational problem for step 1”,“# Define variational problem for step 2” and “# Define variational problem for step 3” demonstrate the variational translation of Eq.(8),Eq.(10)and Eq.(11),respectively.Functions such as “dot” and “nabla_grad” are provided by FEniCS to make the translation more straightforward to mathematicians.“dx” and “ds” indicates the integration over the domain and boundary,respectively,and other work such as splitting linear and bilinear terms as well as integrations will be handled by FEniCS automatically.The second operation is to assign the boundary conditions for each step.The boundary conditions can either be associated with velocity (defined as “bcu” in Fig.2(b))or with pressure (defined as “bcp” in Fig.2(b))” The third operation is to specify solvers for the linear system of equations and solve the problem and in this example the efficient “gmres” algorithm is selected as shown in Fig.2(b).Eventually,based on the Python interface provided by FEniCS,the problem can be easily translated to an efficient finite element code.For more details regarding the implementation of FEniCS,readers are directed to FEniCS’s Tutorial [Langtangen and Logg (2017)].Furthermore,ParaView,an open-source visualization application,was adopted to visualize the computational outcomes.

Figure 2:A part of python code in FEniCS (a)to define variational problems;(b)to evolve right-hand side vector,b,and implement boundary conditions in a timestep loop,where the velocity and pressure boundaries are specified in Step 1 and Step 2,respectively

3.2 Verification case

To verify the implementation of presented solution procedure,a numerical simulation has been performed in solving for a 2D lid-driven cavity problem.In this case,vertical and horizontal velocity on both middle axis of horizontal and vertical has been compared to the solution of Ghia et al.[Ghia,Ghia and Shin (1982)].As shown in Fig.3,fluid flow in a 2D lid-driven cavity model is dominated by the dragging force of container lid.The lid-driven cavity is a well-known benchmark problem for viscous incompressible fluid flow.The vertical dashed line and the horizontal dotted line in Fig.3 indicate the location where velocity profiles shown as dashed line in Figure 4a and dotted line in Fig.4(b)are evaluated,respectively.In the presented case,magnitude of the square is defined as 1 meter,dragging velocity of the lid is set as 1 meter/sec.By comparing to the reference velocity profile shown as discrete points [Ghia,Ghia and Shin (1982)],the solution algorithm producing the velocity profile (both dashed and dotted lines in Fig.4)can be verified.

Figure 3:Schematic of the 2D lid-driven cavity model

Figure 4:The dashed line in Figure 4a and the dotted line in Fig.4(b)are the velocities along x-axis (ux)and y-axis (uy)calculated in the presented study,respectively.The spatial distribution of these velocity value is shown Fig.3,where velocities shown as dashed line is spatially distributed along the dashed line in Fig.3 (vertical center line),and velocities shown as dotted line is spatially distributed along the dotted line in Fig.3 (horizontal center line)

3.3 Computational domains

The discretization of the computational domain is demonstrated in Fig.5,where Fig.5(a),Fig.5(b)and Fig.5(c)present the mesh systems of FEM for Bit Design I,II and III,respectively.The red,blue and black contours represent the inflow boundary where drilling fluid enters the system,the outflow boundary where the drilling fluid leaves the system and no-flow boundary,respectively.

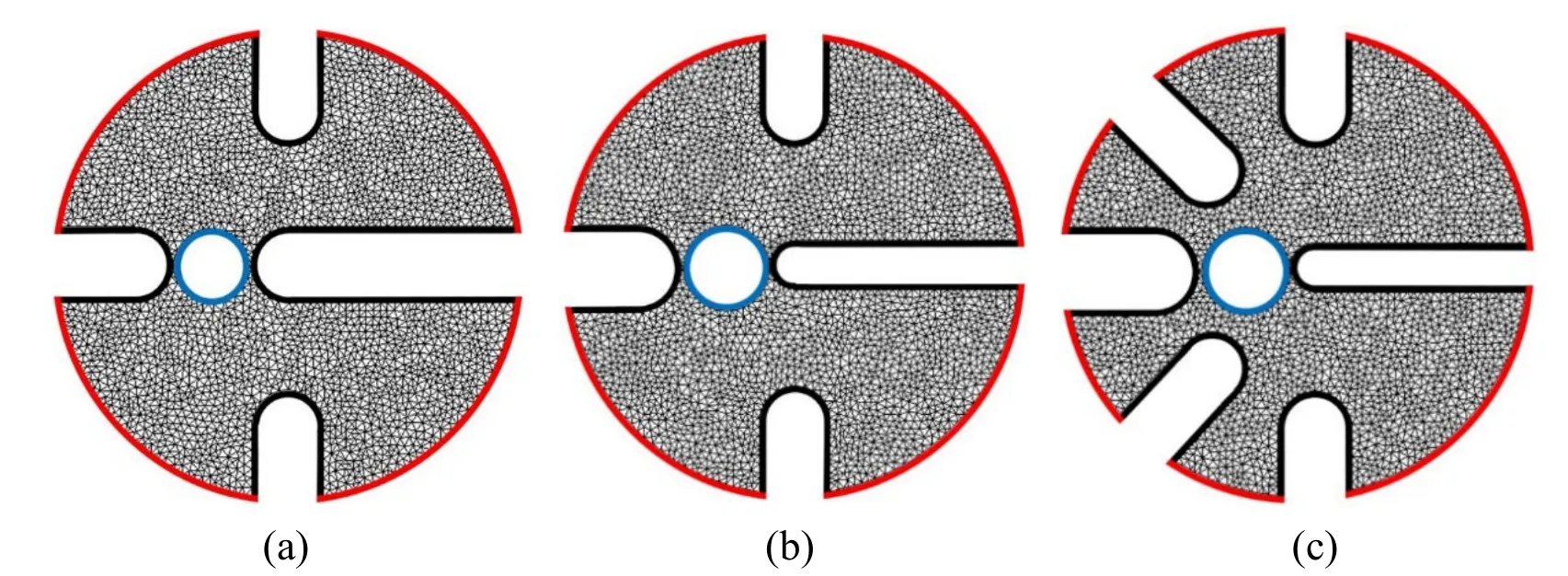
Figure 5:Discretization of computational domains (subfigures are for each of three drill bit designs),where the red contours represent the inflow boundary from which drilling fluid enters the domain and a constant pressure was specified;the blue contours represent the outflow boundary (orifice)from which the drilling fluid leaves the domain and the flux if fixed;the black contours are “walls”,known as no-flow boundaries

4 Result and discussion

Optimal design of gas-lift drilling processes requires a thorough investigation of fluid flow field below the asymmetric drill bits for evaluating the fluid power needed to clean the bottom hole.Pressure and velocity magnitude were computed for three designs of drill bit face.The entire domain is split into several regions,and the average kinetic energy of each region is calculated between blades in order to quantitatively evaluate the balanced fluid power.The formula for kinetic energy is

where E is kinetic energy,J;ρ is the density of gas,kg/m3;A is the area,m2;ℎ is the height of well hole bottle from bit blades (bit blades is 0.0254 meter thick when the bit teeth touch the bottom hole),m;is average velocity,m/s.In this paper,both the area and average velocity of a particular region are approximated numerically based on the mesh system of FEM.The area of a given region is estimated as the sum of the area of each cell in a region,and the average velocityin the region can be estimated by,whereAis the area of a region anduis velocity vector.These calculations can be implemented in FEniCS as shown in Fig.6.Consequently,the fluid volume and mass in the region are Aℎ and Aℎρ,respectively,by assuming an incompressible flow.Three types of parameters are considered in this study,they are geometric parameters,properties,operational parameters,where the geometric parameters are shown in Fig.1 and the properties and operational parameters are indicated in Tab.1.

Figure 6:A part of python code in FEniCS to approximate the area and average velocity in a subdomain defined via calling the function VelMagDomain()

Table 1:Parameters used in the simulation model

4.1 Symmetric design (reference case)

The result of Symmetric Design is shown in Fig.7 as a reference,where Fig.7(a)and Fig.7(b)demonstrate the pressure field and velocity magnitude field,respectively.The highest and lowest pressure value are located at the entry area and exit port,respectively.The symmetric distributed velocity magnitude reaches its peak around the exit port and approaches zero at near blade areas.The entire computational domain of the symmetric design is divided into four regions as labeled in Fig.8.

Figure 7:Pressure field (a)and velocity field (b)of the Symmetric Design

As shown in Fig.8 and Tab.2,the average velocityin region ①,②,③ and ④ are 7.641 m/s,7.659 m/s,7.656 m/s and 7.650 m/s,respectively,which are approximately identical.And the energy per unit volume in each region of the four-blade symmetric design is about 339 J/m3,which is much higher than the required energy per unit volume to remove cuttings (143.4 J/m3).The Symmetric Design generate uniform flow velocities between regions formed by the four blades,but could not drill the formation rock in the center of borehole for the reverse circulation.

Figure 8:The regions between the blades for the Symmetric Design,where the red color indicates each the interested region while the blue color indicates rest of regions;①,②,③,④ are the indices of each region

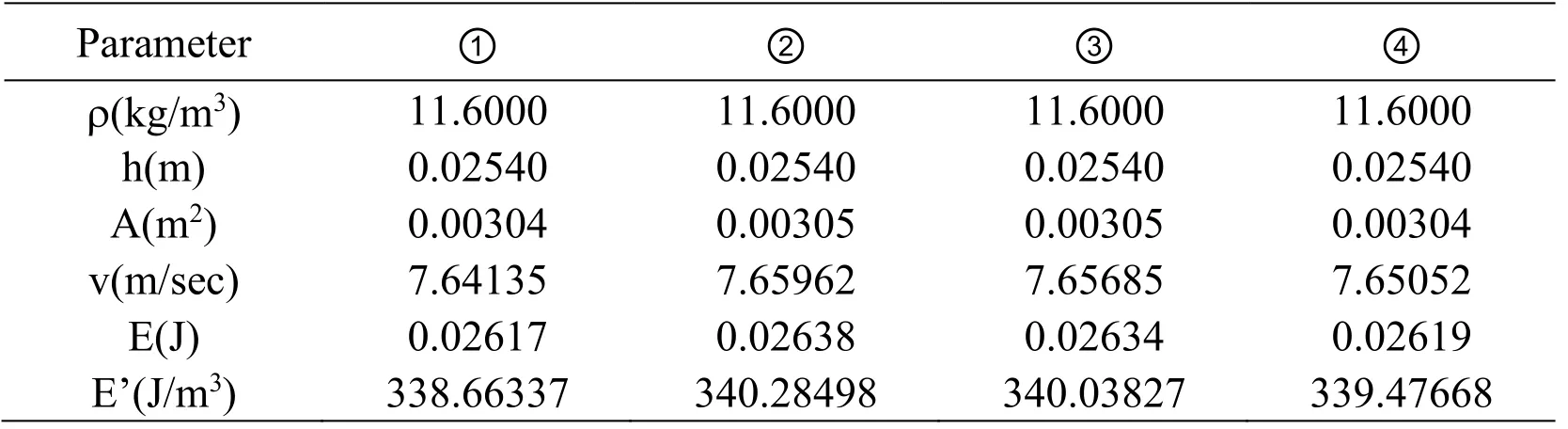
Table 2:The parameters and calculated result in each region between the blades in the Symmetric Design

4.2 Bit Design I

The result of Bit Design I is demonstrated in Fig.9,where Fig.9(a)and Fig.9(b)demonstrate the pressure field and velocity magnitude field,respectively.The highest and lowest pressure value are located at the entry area and exit port,respectively.The velocity magnitude reaches its peak around the exit port and approaches zero at near blade areas.For the velocity magnitude field in Fig.9(b),the velocity value at the left side of that figure are significantly higher than the value in the right-side region.This phenomenon is attributed to the asymmetric inner structure that results in different fluid flow pathways and cross-sectional areas (opening size between blades).Apparently,the longest blade shown in Fig.9(b)increases flow tortuosity and in the other words,increase flow resistance for the fluid in right side regions.In order to generate relatively uniform flow velocities between the four blades,one improvement is to change the size of longest blade and that idea yields the second design,known as a modification of Bit Design I.

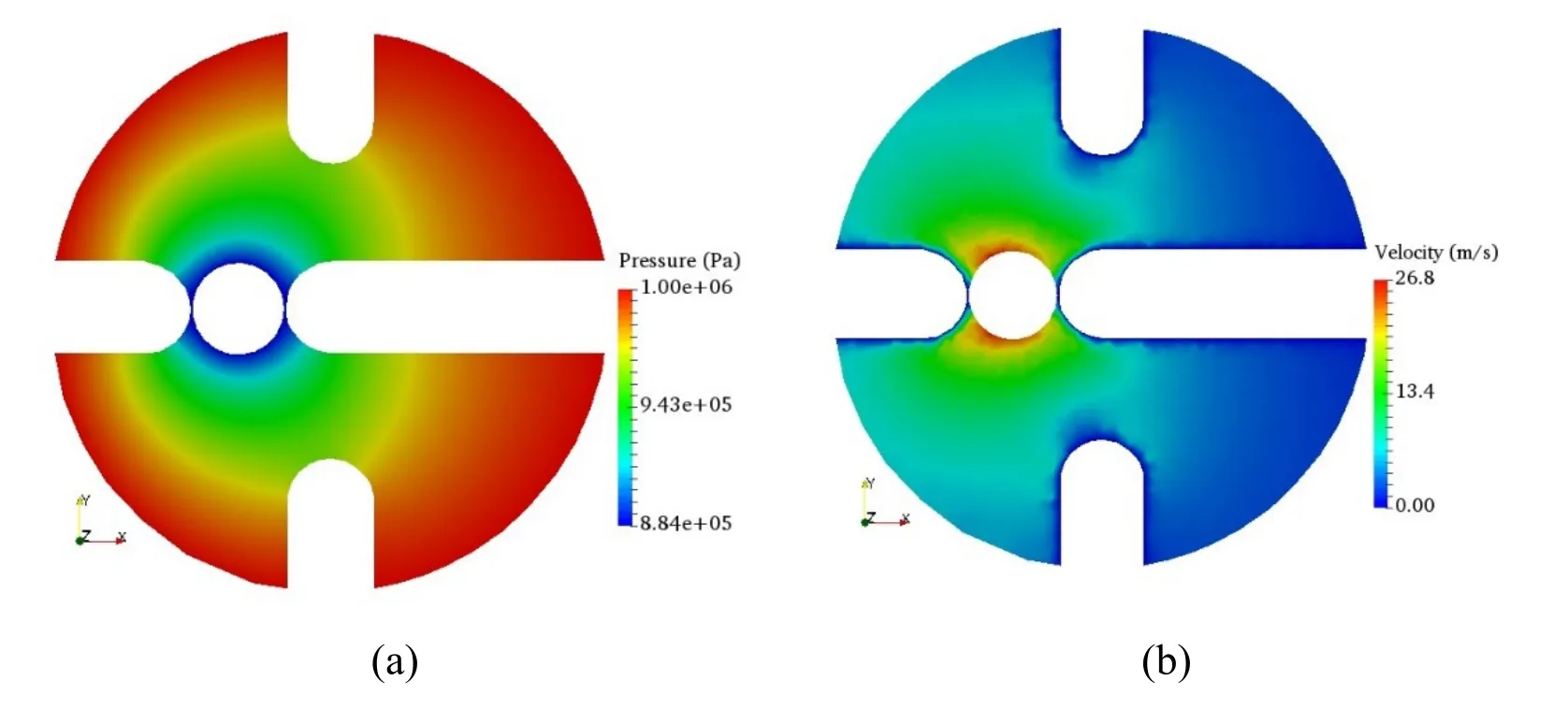
Figure 9:Pressure field (a)and velocity field (b)of Bit Design I

The entire computational domain of Bit Design I was divided into four regions as labeled in Fig.10.As is show in Tab.3,the average velocityin ① and ② are 3.89 m/s and 3.95 m/s,respectively,which are lower than that in region ③ and ④.Correspondingly,the kinetic energy in ① and ② is also lower than that in ③ and ④.Comparing to the Symmetric Design,Bit Design I can drill the center of borehole,but could not generate uniform flow velocities between the four blades.The energy per unit volume of region ① and ② in Bit Design I are 87.57 J/m3and 90.71 J/m3,respectively.Neither of them meets the required energy per unit volume to remove cuttings (143.4 J/m3).Although the energy per unit volume in region ③ and ④ are 470.20 J/m3and 479.53 J/m3,which are much higher than 143.4 J/m3,Bit Design I still cannot clean up borehole effectively.

Figure 10:The regions between the blades for the Bit Design I,where the red color indicates each the interested region while the blue color indicates rest of regions;①,②,③,④ are the indices of each region

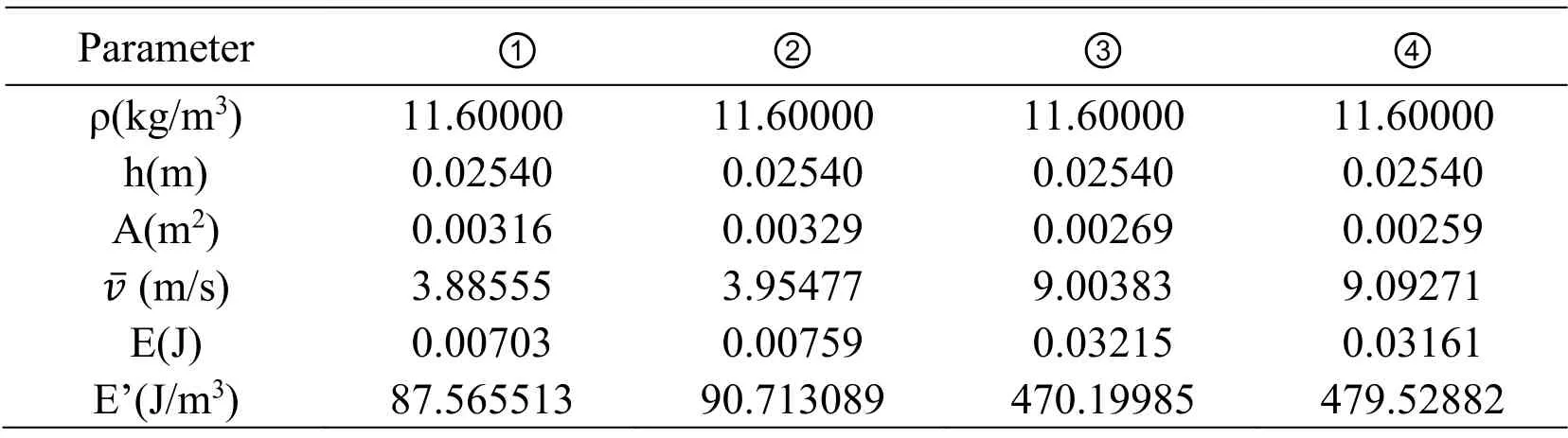
Table 3:The parameters and calculated result in each region of Bit Design I

4.3 Bit Design II

The simulation result for the second design (Bit Design II)is demonstrated in Fig.11,Fig.11(a)and Fig.11(b)indicate the distributions of pressure and velocity magnitude,respectively.

Figure 11:Pressure field (a)and velocity field (b)of Bit Design II

Compared with the velocity field shown in Fig.9(b),the one in Fig.11(b)is a little bit more uniform,implying the Bit Design II is a better design against Bit Design I.However,the velocity magnitude in the left region of Fig.11(b)is still apparently higher than that in the right side.That is because the flow pathway in the left region is still dominant so that most fluid enters the system from left edges.Since the effect of this modified design on improving flow uniformity is limited,another design (Bit Design III)was proposed and studied in this paper,where two more blades are introduced to reduce dominating status of the left-side region of the system via artificially enhancing the flow complexity of that region,and finally it allows fluid entering the system through right side edges.

The entire computational domain of Bit Design II was divided into four regions as labeled in Fig.12.As is show in Tab.4,the average velocity in ① and ② are 4.07 m/s and 4.15 m/s,respectively,which are slightly higher than the average velocity of ① and ② in Tab.3.Comparing to Bit Design I,Bit Design II presents very limited improvement.The energy per unit volume of region ① and ② for Bit Design I are 87.57 J/m3and 90.71 J/m3,respectively.While the energy per unit volume of region ③ and ④ for Bit Design II are increased to 96.22 J/m3and 99.97 J/m3approximately by 9.84% and 10.21%,respectively.However,neither of them reaches the required critical energy per unit volume (143.4 J/m3),meaning that Bit Design II cannot remove drill cutting effectively either.

Figure 12:The regions between the blades for the Bit Design II,where the red color indicates each the interested region while the blue color indicates rest of regions;①,②,③ and ④ are the indices of each region

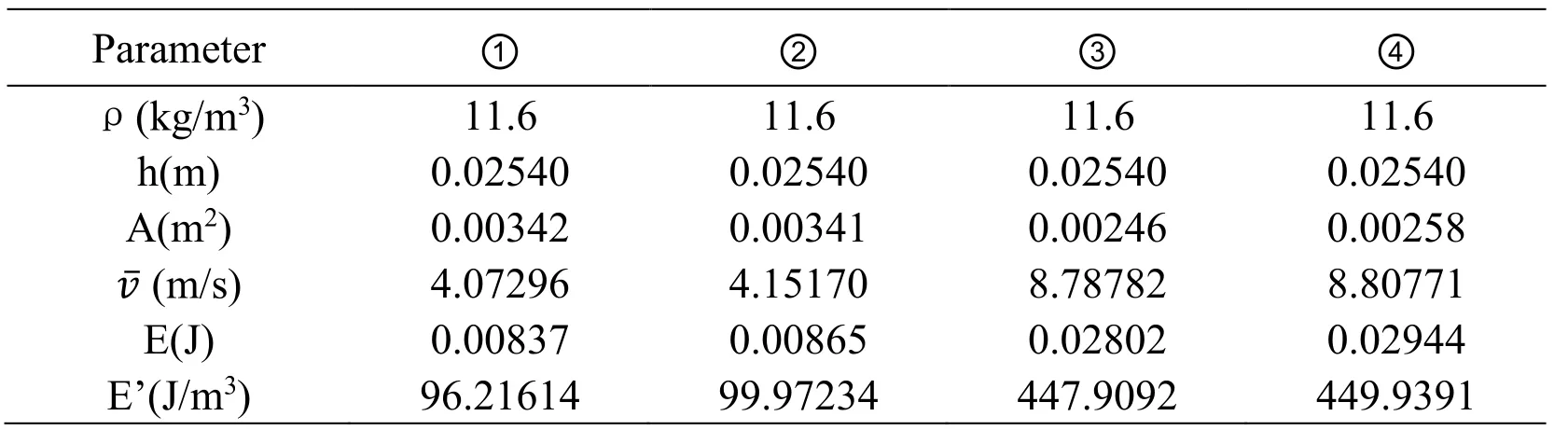
Table 4:The parameters and calculated result in each region of Bit Design II

4.4 Bit Design III

Fig.13 presents the simulation result of the Bit Design III,including both pressure field as well as velocity field.Compared with previous designs,the flow velocity distribution in Fig.13(b)is much more uniform,with higher velocity value because of the structural complexity of the system.Around the exit port,velocity magnitude is evenly distributed,to ease the removal of drilling cuttings at the bottom of the well.Compared with Bit Design I and II,the Bit Design III is superior,because it generates relatively uniform flow velocities between blades,which provides balanced fluid power needed to clean all bit teeth on the bit blades.Different from the Bit Design I and Bit Design II,the Bit Design III consists of six regions as labeled in Fig.14.As is shown in Fig.14 and Tab.5,the average velocityin ① and ② is 7.81m/s and 7.89 m/s,respectively,which are much higher than the average velocityof ① and ② in Bit Design II.The kinetic energy present very little difference between each highlighted region in Fig.14,which implies that the Bit Design III generates relatively uniform flow velocities between the blades.In addition,for Bit Design III,the energy per unit volume in each of six regions is higher than the critical energy per unit volume of fluid required to remove cuttings.Even the region ① presents the energy of 353.62 J/m3that is still much larger than the required value.Therefore,Bit Design III generates relatively uniform regional velocities and provides balanced fluid power needed to clean all bit teeth on the bit blades.

Figure 13:Pressure field (a)and velocity field (b)of Bit Design III

Figure 14:The regions between the blades for the Bit Design III (subfigures are six regions)where the red color indicates each the interested region while the blue color indicates rest of regions;①,②,③,④,⑤ and ⑥ are the indices of each highlighted region

Table 5:The parameters and calculated result in each region of Bit Design III

5 Conclusions

Finite Element Method (FEM)was used to calculate the pressure and velocity fields below the drill bit faces of three designs.The following conclusions are drawn:

1.Bit Design I shown in Fig.1(a)for a bit with equal-width blades and small port does not create balanced flow power between blades.Gas flows much faster in the near-port region than in the far-port region where it will not clean the bit teeth.Bit Design I can drill the formation rock in the center of borehole but could not generate uniform flow velocity field in the regions between the four blades.According to the critical energy per unit volume of fluid required to remove cuttings (143.4 J/m3),only the regions ③ and ④ in Bit Design I present enough capability to remove cuttings.

2.Bit Design II shown in Fig.1(b)has non-equal-width blades and a large port.The flow field is similar to Bit Design I,meaning that increasing blade width and port size will not significantly improve flow field performance to clean the bit.Comparing to Bit Design I,Bit Design II presents very limited improvement,and still could not meet the requirement of borehole cleanup.The energy per unit volume of region ① and ② for Bit Design I are 87.57 J/m3and 90.71 J/m3,respectively.While the energy per unit volume of region ③ and ④ for Bit Design II are increased to 96.22 J/m3and 99.97 J/m3approximately by 9.84% and 10.21%,respectively.However,neither of them reaches the required critical energy per unit volume (143.4 J/m3).

3.Bit Design III shown in Fig.1(c)has more blades in the near-port-half space.The added blades significantly improve flow field to achieve a much better flow power balance between blades and thus bit cleaning.For Bit Design III,the energy per unit volume in each of six regions is higher than the critical energy per unit volume of fluid required to remove cuttings.Even the region ① presents the energy of 353.62 J/m3that is still much larger than the required value.Therefore,Bit Design III generates relatively uniform regional velocities and provides a balanced fluid power needed to clean all bit teeth on the bit blades.

Acknowledgements:This research was supported by the Open Fund (PLN201704)of the China State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation at the Southwest Petroleum University and the China National Natural Science Foundation Founding Nos.51874252,51534006 and 51674044.This research was also supported by the China Scholarship Council Founding No.201808510219.