Dynamic Analyses of a Simply Supported Double-Beam System Subject to a Moving Mass with Fourier Transform Technique

Lizhong Jiang ,Xilin Chai ,Zhihua Tan ,Wangbao Zhou , ,Yulin Feng ,Zhipeng Lai and Lan Zheng

Abstract: In order to study the dynamic characteristics of a simply supported double-beam system under a moving mass,the system of fourth-order dynamic partial differential equations of a simply supported double-beam system was transformed into a system of second-order dynamic ordinary differential equations relative to time coordinates by performing the finite sin-Fourier Transform relative to space coordinates.And the analytical solution of the dynamic response of the simply supported double-beam system under a moving mass was obtained by solving the system of dynamic ordinary differential equations.The analytical method and ANSYS numerical method were used to calculate the dynamic responses of several simply supported double-beam systems under a moving mass at different speeds.The influences of inertial effect,mass movement speed,and Winkler-layer spring stiffness and damping on the dynamic responses of simply supported double-beam systems were analyzed.According to the study results,the analytical calculation results in this paper fit well with the ANSYS finite element numerical calculation results,demonstrating the rationality of the analytical method.The inertial effect has a significant influence on the dynamic response characteristics of the simply supported double-beam system.The simply supported double-beam system underwent several resonant speeds under a moving mass,and the Winkler-layer spring stiffness has a relatively significant effect on the vibration of the first beam.

Keywords: Double-beam system,moving mass,dynamic response,analytical method,finite sin-Fourier Transform.

1 Introduction

The dynamic response problem of beam-type structures under a vehicle has a great importance in many engineering applications such as highway bridges,railways bridges,and aircraft/taxiway bridges in airports [Lai and Ho (2016);Ghafarian and Ariaei (2016);Jia,Zhao,Li et al.(2018);Lai,Hanzic and Ho (2019);Lee (1998);Sadek,Abualrub,Abukhaled (2007);Tsukazan (2005);Yang and Yau (2017);Zhang,Jia,Zheng et al.(2016)].Therefore,accurately predicting the dynamic response of beam-type structures is of great significance in engineering applications [Yan,Zhao,Sun et al.(2019);Beskou and Theodorakopoulos (2011);Gou,Yang,Leng et al.(2018);Miao,Shi,Luo et al.(2018);Rusin,Śniady and Śniady (2011);Tan,Guan and Zhang (2018);Wu,Zhou,Gao et al.(2019);Yan and Ren (2016)].

In traditional studies,researchers generally simplified a vehicle to the so-called moving load [Kim and McCullough (2003);Yang,Chen,Xiang et al.(2008);Zheng,Cheung,Au et al.(1998)].Yang et al.[Yang,Chen,Xiang et al.(2008)] investigated the free and forced vibration of slender functionally graded material beams with open edge cracks under a combined action of an axial compression and a concentrated transverse moving load.Şimşek et al.[Şimşek and Cansız (2012)] and Wu et al.[Wu and Gao (2015)] investigated the dynamic response of a simply supported viscously damped double-beam system under moving harmonic loads.Ariaei et al.[Ariaei,Ziaei-Rad and Ghayour (2011)] investigated a unique yet method of obtaining the exact solution for the vibration of an undamped multibeam system due to a moving load.However,one disadvantage of the moving load model is that the interactions between vehicle and bridge are neglected [Lee (1998)],and thus it cannot truly reflect the dynamic response characteristics of a bridge across,which the vehicle runs.In addition,considering the moving load model is correct and effective only when the vehicle has a small mass (relative to the mass of the bridge)and a low speed [Yang and Lin (2005)],it is no doubt unreasonable for bridge design.

According to recent developments in structural materials and constructional technologies [Zhou and Wang (2019);Jiang,Feng,Zhou et al.(2019);Li,Liu,Yu et al.(2019);Zhang,Liu,Wang et al.(2019)],the structures are likely to be affected by sudden changes in masses and substructure elements,in which the inertia effect of a moving mass is not negligible [Dehestani,Mofid and Vafai (2009);Lai,Chen,Ren et al.(2019);Jiang,Feng,Zhou et al.(2018);Feng,Jiang,Zhou et al.(2019)].Considering the inertial effect of vehicle mass into account,a vehicle can be simplified as moving mass [Nikkhoo,Rofooei and Shadnam (2007);Nikkhoo,Farazandeh,Hassanabadi et al.(2015)].In a recent study,the related problem of beam-type structures under a moving mass has been studied extensively.Gu et al.[Gu and Cheng (2004)] modeled a ball screw as a high-speed rotating shaft using Timoshenko beam theory and a nut as a moving concentrated mass.Gbadeyan et al.[Gbadeyan and Dada (2006)] investigated the elastodynamic response of a rectangular Mindlin plate subjected to a distributed moving mass.The set of governing characteristic partial differential equations that include the effects of shear deformation and rotary inertia has been expressed in its dimensionless form.Kargarnovin et al.[Kargarnovin,Ahmadian and Jafari-Talookolaei (2012)] presented the dynamic response of a delaminated composite beam under the action of moving oscillatory mass.The Poisson’s effect,shear deformation,and rotary inertia have been considered in this analysis.Pirmoradian et al.[Pirmoradian,Keshmiri and Karimpour (2015)] studied a Timoshenko beam excited by a sequence of identical moving masses as a time-varying problem.The effects of centripetal and Coriolis accelerations besides the vertical component of acceleration of the moving mass are considered.A range of analysis methods has been proposed to study the dynamic responses of bridges under moving mass.Yavari et al.[Yavari,Nouri and Mofid (2002)] analyzed the dynamic response of Timoshenko beams under moving mass using a numerical method called discrete element technique.Ariaei et al.[Ariaei,Ziaei-Rad and Ghayour (2009)] presented an analytical approach,as well as a calculation method for determining the dynamic response of the undamped Euler-Bernoulli beams with breathing cracks under a point moving mass using the so-called discrete element technique and the finite element method.Eftekhari et al.[Eftekhari and Jafari (2012,2014)] proposed multiple methods that are the finite element method,the differential quadrature method,the integral quadrature method,and the triangular quadrature rule to study the transient response of rectangular plates subjected to moving masses.Ye et al.[Ye and Chen (2009)] proposed a moving finite element method to perform the dynamic analysis of a simply supported beam for a moving mass.Kiani et al.[Kiani,Nikkhoo and Mehri (2010)] studied the dynamic response of multispan viscoelastic thin beams subjected to a moving mass by a generalized moving least square method.Şimşek [Şimşek (2010)] investigated the vibration of a functionally graded simply-supported beam due to a moving mass by using Euler-Bernoulli,Timoshenko and the third order shear deformation beam theories.Ariaei [Ariaei,Ziaei-Rad and Malekzadeh (2013)] presented an analytical transfer matrix method to determine the effect of intermediate flexible constraints on the dynamic behavior of a multi-span beam subject to a moving mass.However,most of the existing methods are finite element numerical method [Ariaei,Ziaei-Rad and Ghayour (2009);Yavari,Nouri and Mofid (2002)],semi-analytical method [Eftekhari and Jafari (2012,2014);Ye and Chen (2009)],or more complex analytical method [Ariaei,Ziaei-Rad and Malekzadeh (2013);Kiani,Nikkhoo and Mehri (2010);Şimşek (2010)],which results in low computational efficiency in solving the dynamic response of beams under moving mass.In addition,they mainly focused on the dynamic responses of single-beam systems,but rarely considered the dynamic responses of double-beam systems under moving load [Jiang,Zhang,Feng et al.(2019);Nguyen (2016);Shen,Jiang,Zhang et al.(2018);Şimşek (2011)].

These studies indicate that although the dynamic responses of beam-like structure under moving mass has been investigated profoundly in a way and laid a theoretical basis for the engineering applications of beam-like structure,studies on the dynamic response of a beam mainly focused on single-beam models,and many researches have some limitations.For example,the analytical expression form is too complex to solve,which results in low computational efficiency,and the materials and geometric properties of each beam are required to be identical.Therefore,for further simplifying the process of calculating the dynamic responses of double-beam systems under moving mass,in this study,we proposed a simple and efficient method of solving the dynamic response of a simply supported double-beam system under moving mass based on the finite sin-Fourier Transform theory.Taking a typical simply supported double-beam system in Beijing-Shanghai railway system as an example,the analytical calculation results of this paper were compared with the ANSYS finite element numerical calculation results,demonstrating the correctness and reliability of the proposed analytical method.Then the influences of inertial effect,mass movement speed,Winkler-layer spring stiffness and damping on the dynamic responses of simply supported double-beam systems were analyzed,offering a reliable and effective theoretical basis for solving practical engineering problems.

2 Mathematical model and governing equations

When a vehicle passes through a simply supported double-beam system at uniform speed,it can be simplified as the analytical model shown in Fig.1.Assuming that the motion of the beam is under small deformation and within the elastic range,the vibration differential equation of simply supported double-beam system under the action of moving mass can be expressed as follows [Lai,Jiang and Zhou (2018)]:

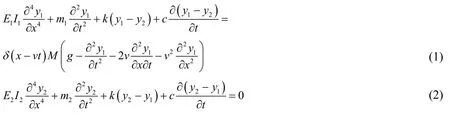
whereyi(x,t)i= 1,2;Eii= 1,2;Iii= 1,2 andmii= 1,2 represent the deflections,elastic moduli,horizontal moments of inertia and per-unit-length beam masses of the first beam,and the second beam,respectively;krepresents the Winkler-layer spring stiffness between the first beam and the second beam;crepresents the Winkler-layer spring damping between the first beam and the second beam;δrepresents Dirac function;vrepresents load movement speed;Mrepresents the size of moving mass.

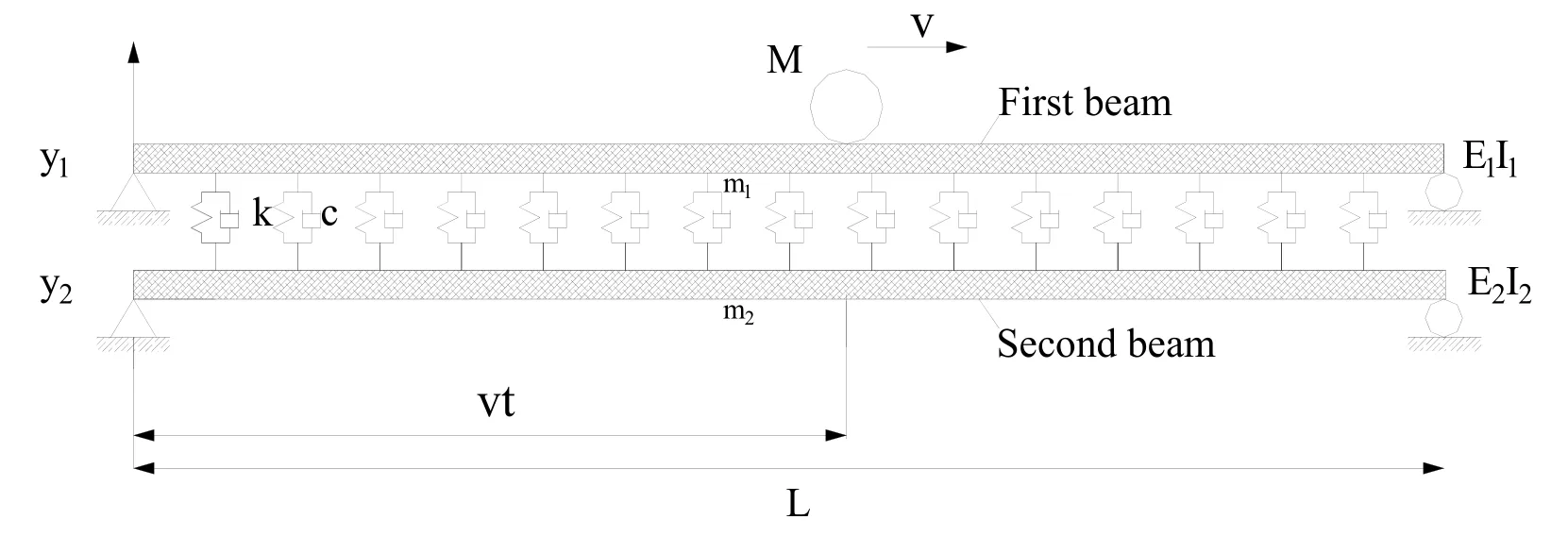
Figure 1:Simply supported double-beam system under moving mass

To solve the above partial differential equations system of vibration,first of all,the finite sin-Fourier Transform for space coordinatexwas performed,and for 0x L≤ ≤ ,it is defined as follows:

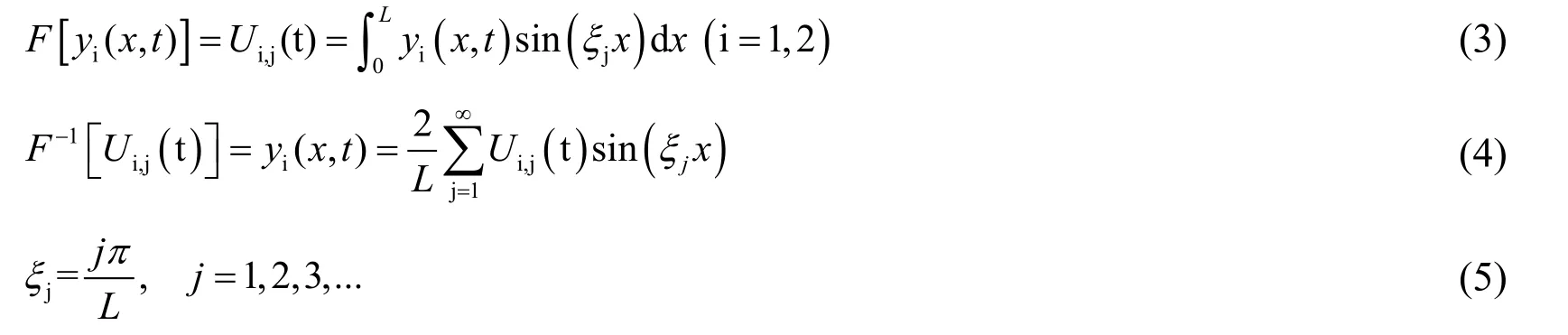
Under minor deformation conditions,the boundary condition of the simply supported beam system can be written as:

According to the boundary condition,the finite sin-Fourier Transform of the fourth-order derivative of the displacement function relative to coordinatexcan be obtained:

Performing finite sin-Fourier transform for both sides of Eqs.(1)and (2)relative to coordinatexleads to the following equation:

Substituting Eq.(4)into Eq.(8)results in:

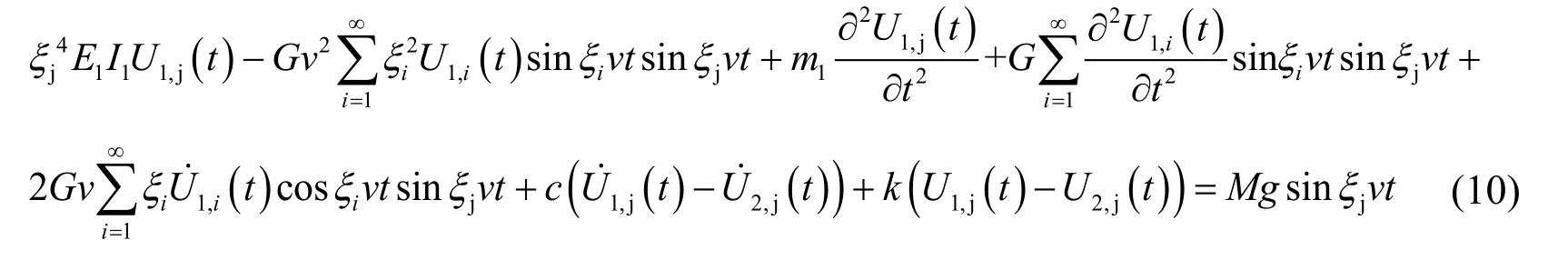
Eqs.(9)and (10)can be further expressed as:

3 Equation solution

Due to the continuous change in the position of moving mass on the simply supported double-beam system,the mass matrix,damping matrixand stiffness matrixin Eq.(11)all constantly change with the passage of time.As a result,the governing equations of the simply supported double-beam coupled system under moving mass denotes a system of differential equations with second-order time-varying coefficients,and the coefficient matrixesandof the equations also change with the movement parameterv.In general,for such differential equations systems,the most effective and common methods are step-by-step integration methods.At present,the frequently used step-by-step integration methods include the linear acceleration method,Willson-θmethod,and Newmark-βmethod.The Newmark-βmethod was employed in this study.

Assuming that two groups of unknown variables (t t+Δη ,and)att+Δtmeet a dynamic equation,i.e.,

Assuming the speed and displacement att+Δtas

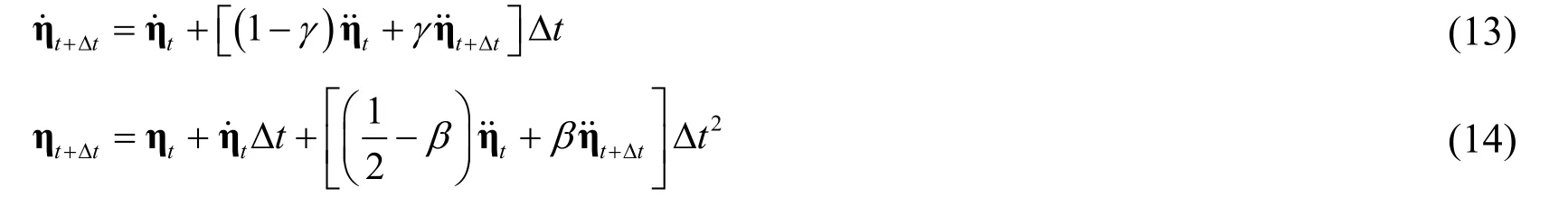
where ,γ βrepresent the Newmark parameters.The acceleration,speed,and displacement att+Δtcan be obtained by sorting out and substituting related equations:

where

Solve η at each moment by employing Newmark-βstep-by-step integration method,i.e.,{Uj} in Eq.(11),then the deflection of any point on the simply supported double-beam system at any moment can be further obtained by Eq.(4).

4 Analysis of example and applications of the analytical method

4.1 Verification of the analytical method

A typical simply supported double-beam system in Beijing-Shanghai railway system is taken as an example.In this system,the first beam is a rail,and the second beam is a typical simply supported bridge.The material properties and geometric parameters are as follows:span:L= 32 m;moving mass:M= 8500 kg ;elastic moduli of the first beam and the second beam:E1= 2.06 ×1011Pa ,E2= 3 .5 × 1 010Pa;line masses of the first beam and the second beam:m1=60 kg/m,m2=3 6000 kg/m;Winkler-layer spring stiffness and damping:k= 6 × 107N/m2,c=9.625 ×104N ⋅s/m2;moments of inertia of the first beam and the second beam:I1=3 .217× 1 0-5m4,I2=10.42 m4;densities of the first beam and the second beam:ρ1=7 .85 × 103kg/m3,ρ2=2.5 × 103kg/m3.

To verify correctness of proposed analytical method,the ANSYS finite element numerical method was employed to calculate the dynamic responses of the above simply supported double-beam system under the moving mass at different speeds,and the calculation results of the two methods were compared.The proposed analytical method was compiled in MATLAB R2016a [MATLAB (2016)].Regarding the ANSYS finite element model,the BEAM3 element was used to model the first beam and the second beam.The Winklerlayer spring and damping between the first beam and the second beam were modeled by COMBIN14 elements,and the spacing between the COMBIN14 elements was set as 0.032 m.The moving mass was modeled by the MASS21 element and was coupled with the first layer beam by coupling displacement.The simplified support constraints were modeled by restricting the degree of freedom at the two ends of the model in x and y directions.The comparison results are shown in Tab.1 and Figs.2-3.In Tab.1,mFandmSrepresent the analytical method results of the dynamic response peaks of the mid-span deflection of the first beam and the second beam,respectively;aFandaSrepresent the ANSYS numerical calculation results of the dynamic response peaks of the mid-span deflection of the first beam and the second beam,respectively;andrepresent the errors between the calculation results obtained by the two methods for the dynamic response peaks of the mid-span deflections of the first beam and the second beam,respectively.

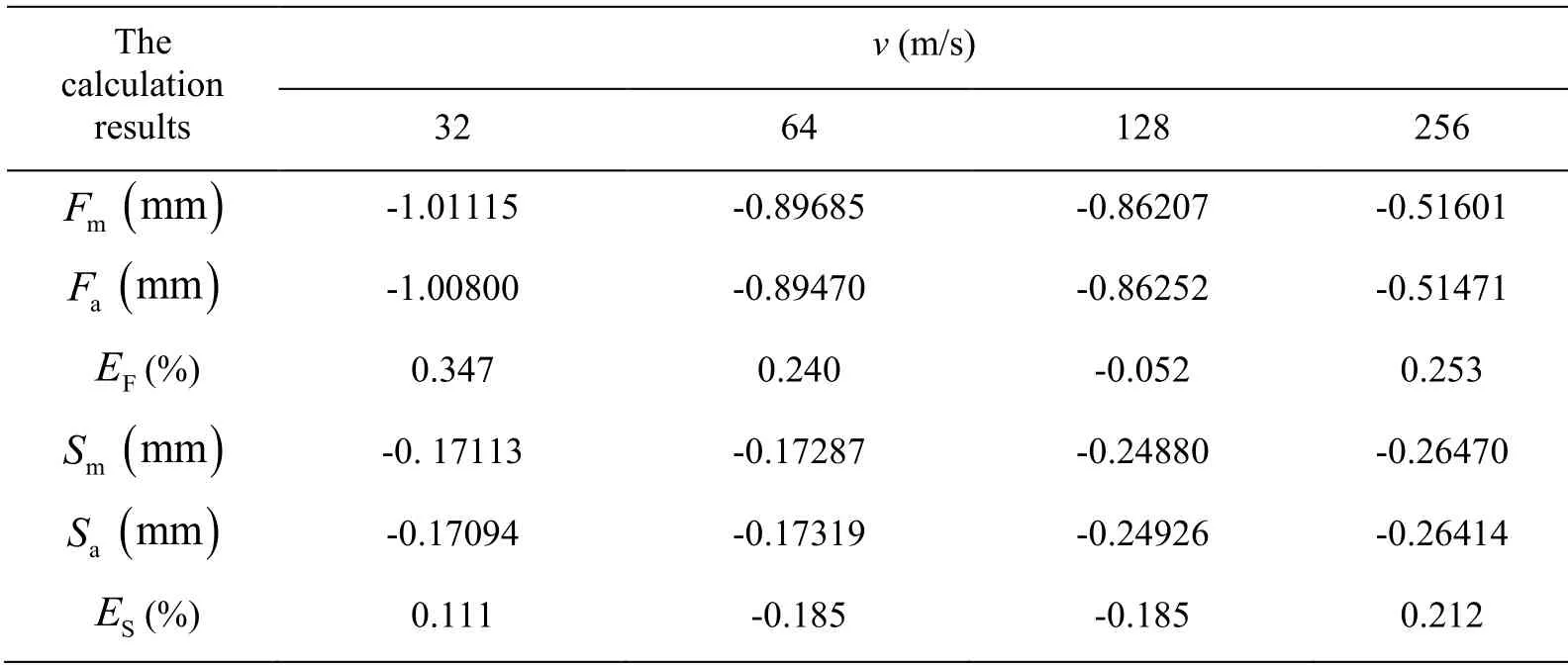
Table 1:Comparison of the calculation results for the dynamic response peaks of the midspan deflections of the simply supported double-beam system at different speeds

According to Tab.1,under moving mass at different speeds,the errors between the calculation results obtained by the two methods for the dynamic response peaks of the midspan deflections of the second beam were 0.347%,0.240%,0.052%,and 0.253%,respectively,all less than 0.5%.Meanwhile,according to Figs.2-3,under moving mass at different speeds,the dynamic response time-history curves of the mid-span deflections of the simply supported double-beam system calculated by the analytical method and ANSYS finite element numerical method fitted well,further demonstrating the correctness of the analytical method proposed in this study.

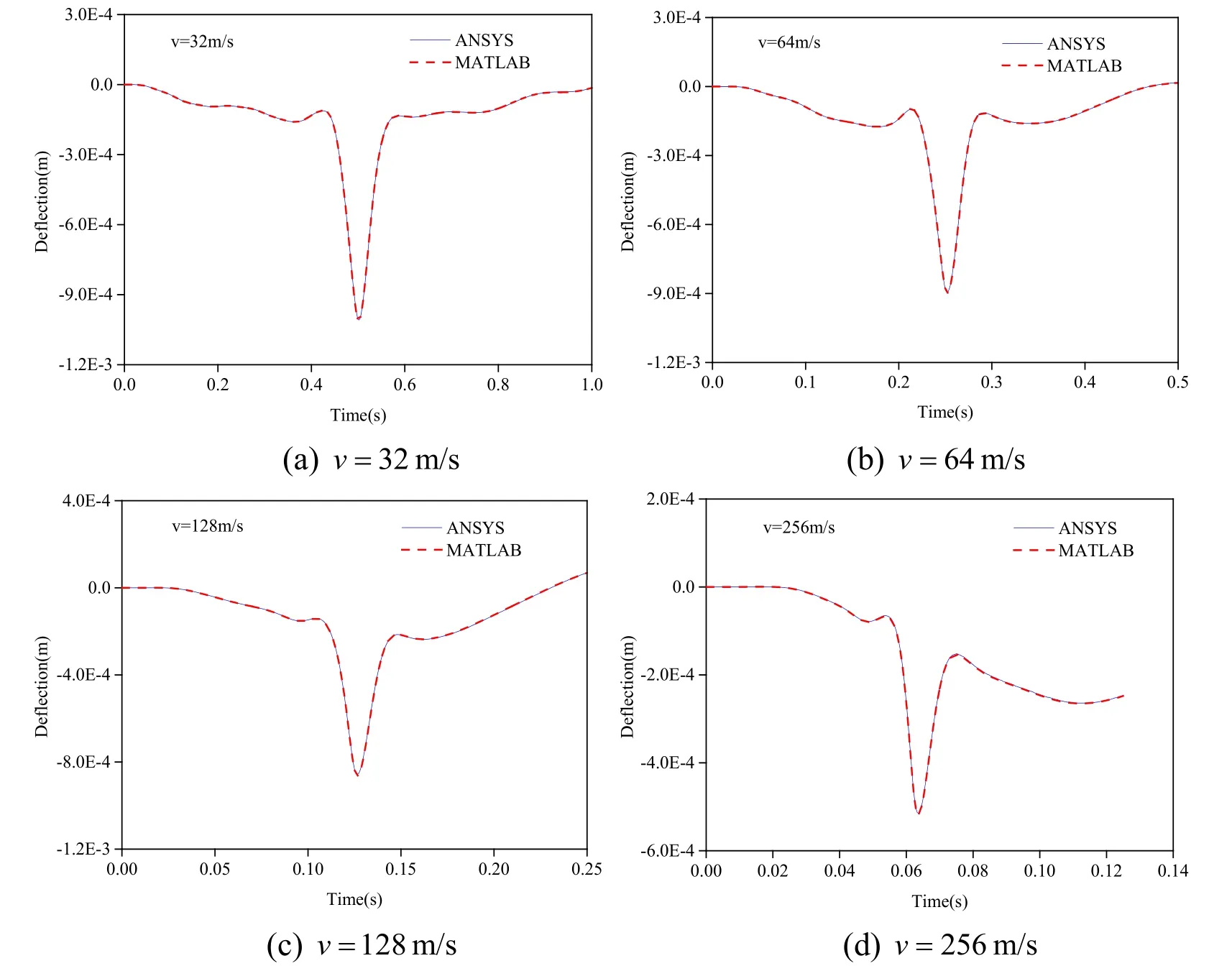
Figure 2:Comparison of the calculation results for the dynamic response time-history curves of the mid-span deflections of the first simply support beam at different speeds

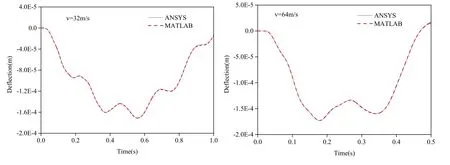
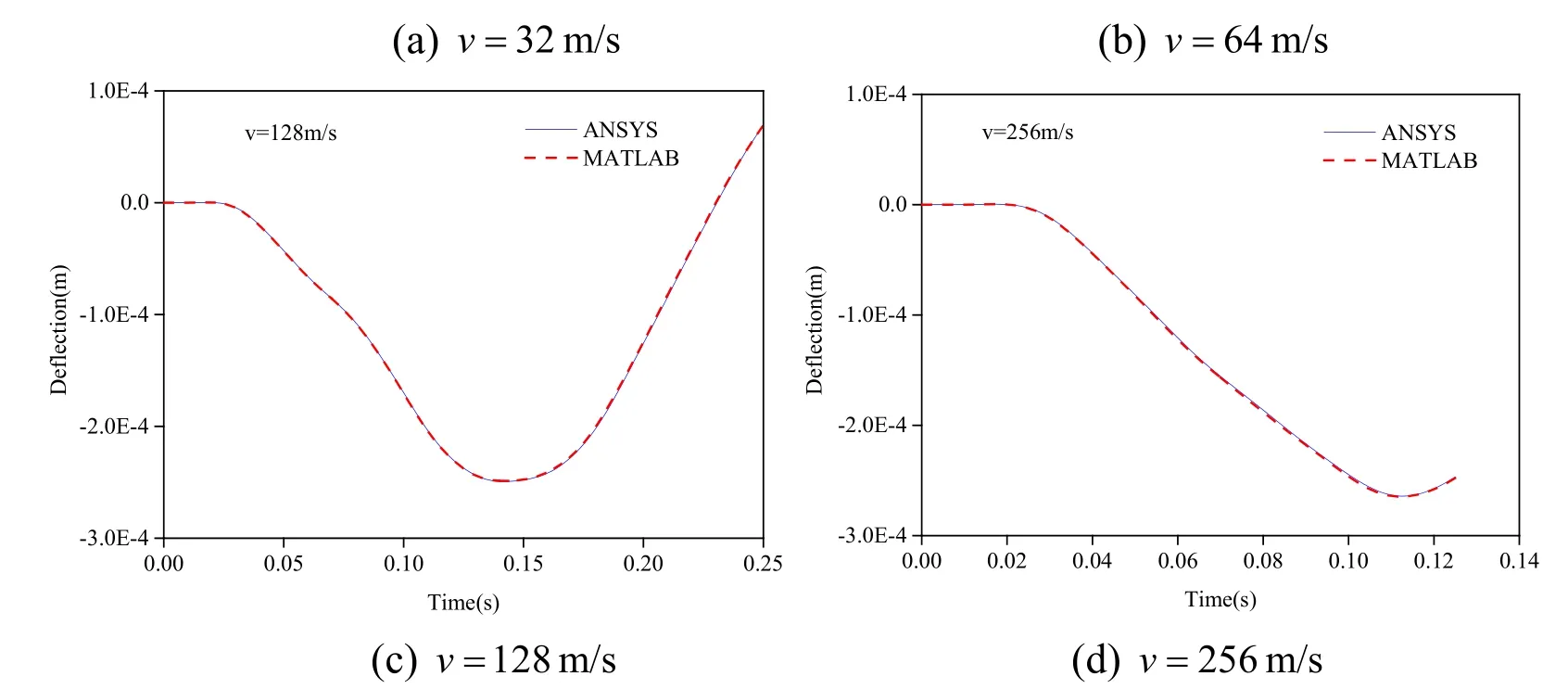
Figure 3:Comparison of the calculation results for the dynamic response time-history curves of the mid-span deflections of the second simply support beam at different speeds

4.2 Influence of moving mass on maximum deflection of double simply supported beams

In order to study the influence of moving mass on inertial effect,the analytical method proposed in this study was used to calculate the dynamic responses of the simply supported double-beam system under different moving masses at the same movement speed (v= 32 m/s )according to two circumstances,i.e.,considering the inertial effect and without considering inertial effect.The comparison results are shown in Tab.2,Fig.4 and Fig.5.In Tab.2,andrepresent the errors due to inertial effect for the dynamic response peaks of the mid-span deflections of the first beam and the second beam,respectively;Fm′ andSm′ represent the analytical calculation results,regardless of inertial effect,of the dynamic response peaks of the mid-span deflections of the first beam and the second beam,respectively.

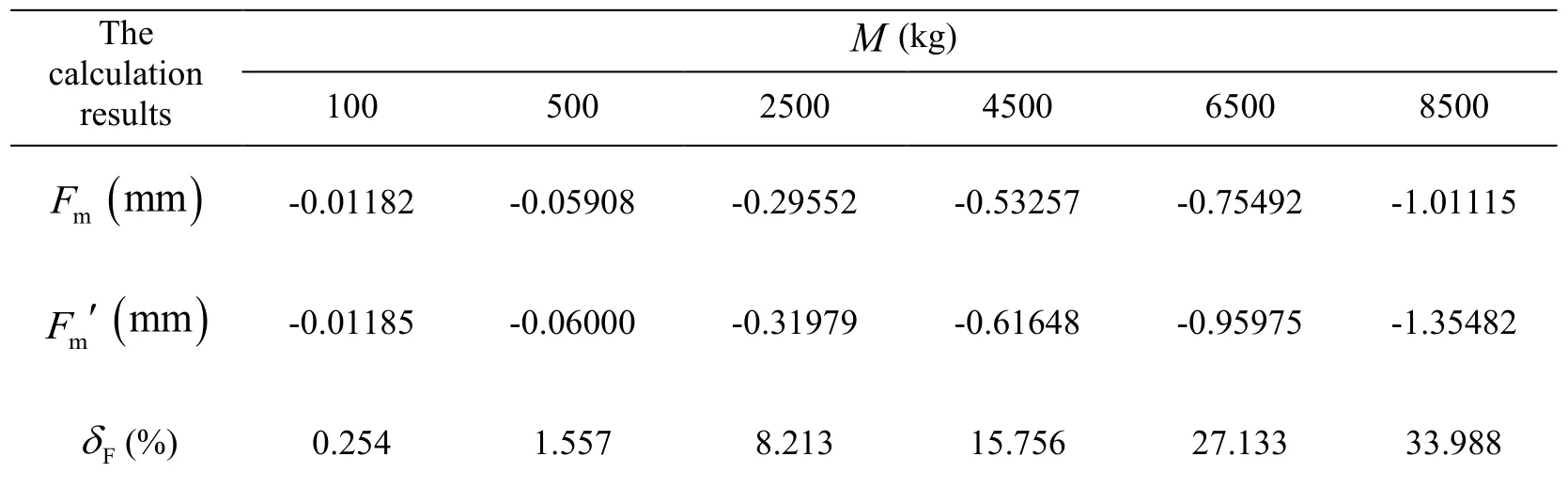
Table 2:Comparison of the calculation results for the dynamic response peaks of the midspan deflections of the simply supported double-beam system under different moving masses

S ( )m mm -0.00203 -0.01015 -0.05067 -0.09105 -0.13126 -0.17113 S ′ ( )m mm -0.00204 -0.01031 -0.05491 -0.10573 -0.16406 -0.23167 Sδ (%)0.493 1.576 8.368 16.123 24.989 35.377

Figure 4:Comparison of the calculation results for the dynamic response time-history curves of the mid-span deflections of the first simply support beam under different moving masses

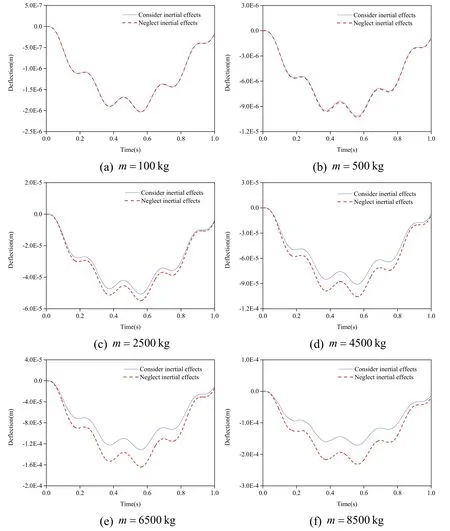
Figure 5:Comparison of the calculation results for the dynamic response time-history curves of the mid-span deflections of the second simply support beam under different moving masses

According to Tab.2,Fig.4 and Fig.5,when the moving mass was 100 kg,the errors in the dynamic response peaks of the mid-span deflections of the first beam and the second beam were all less than 0.5%.The results suggested that when the moving mass was small relative to the mass of the first beam,inertial effect only had an insignificant influence on the dynamic responses of the mid-span deflections of the simply supported double-beam system.However,when the moving mass was 8,500 kg,the errors in the dynamic response peaks of the mid-span deflections of the first beam and the second beam uniformly exceeded 33%,suggesting that when the moving mass was large relative to the mass of the first beam,the influence of inertial effect on the dynamic responses cannot be neglected.

4.3 Influence of moving mass speed on maximum deflection of double simply supported beams

In order to study the influence of speed on inertial effect,the proposed analytical method was also used to calculate the dynamic responses of the simply supported double-beam system at the same mass ratioλ(λ=M/M1,Mrepresents the moving mass,M1represents the mass of the first beam)but at different movement speeds according to two circumstances,i.e.,considering the inertial effect and without considering the inertial effect,and the calculation results of the dynamic response peaks of the mid-span deflections of the simply supported double-beam system were also compared,and the comparison results are shown in Figs.6-9.

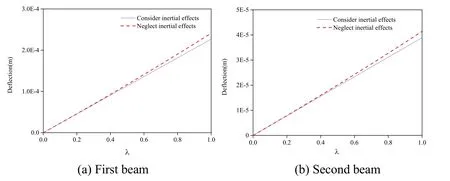
Figure 6:Comparison of the calculation results for the dynamic response peaks of the midspan deflections of the simply supported double-beam system at 32 m/sv=

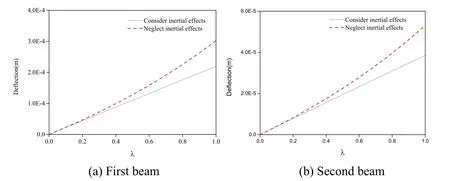
Figure 7:Comparison of the calculation results for the dynamic response peaks of the midspan deflections of the simply supported double-beam system at v= 64 m/s

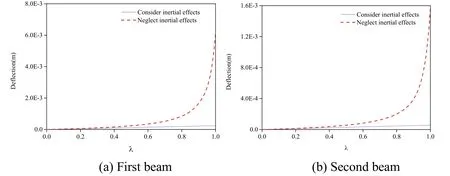
Figure 8:Comparison of the calculation results for the dynamic response peaks of the midspan deflections of the simply supported double-beam system at v= 128 m/s

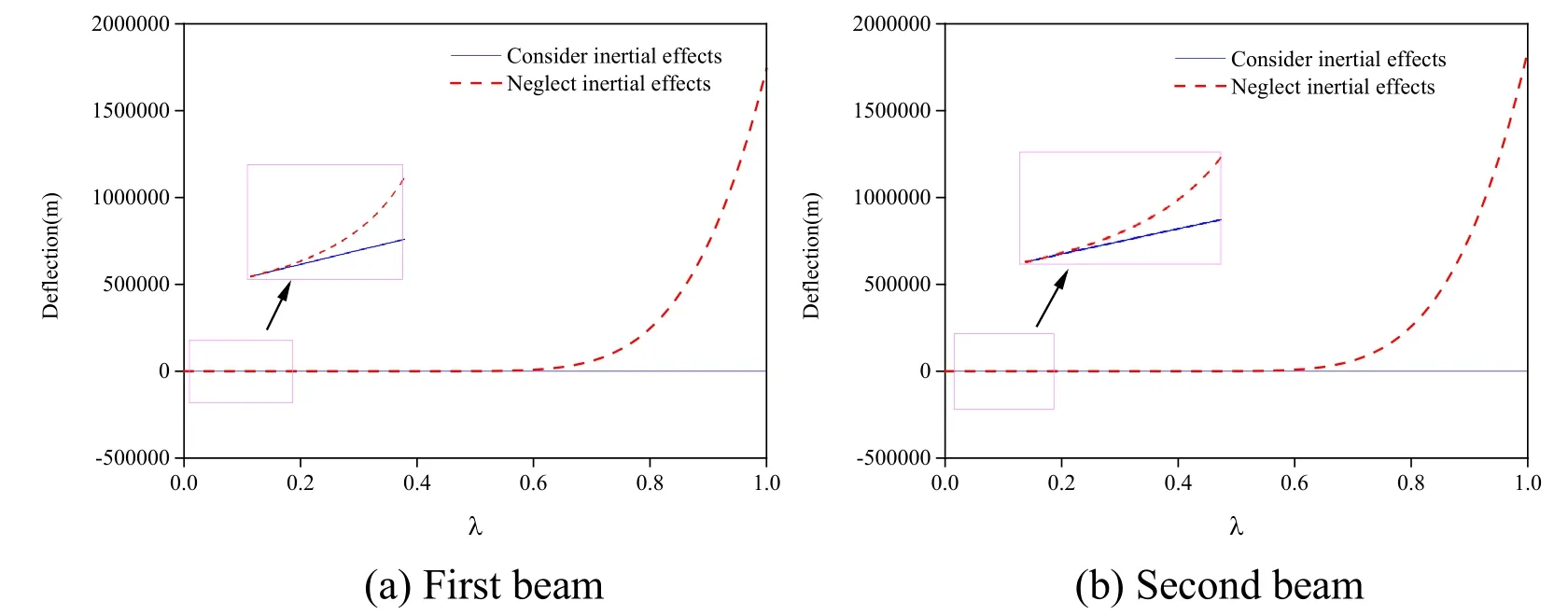
Figure 9:Comparison of the calculation results for the dynamic response peaks of the midspan deflections of the simply supported double-beam system at v= 256 m/s

According to Figs.6-9,when the mass ratio was less than 0.2,inertial effect always had a relatively small influence on the calculation results of the dynamic response peaks of the mid-span deflections of the simply supported double-beam system regardless of the movement speed.However,when the mass ratio exceeded 0.2,with the movement speed increasing,the influence of inertial effect on the calculation results of the dynamic response peaks of the mid-span deflections gradually enhanced.When the movement speed reached 256 m/s,without considering the inertial effect,the calculation results of the dynamic response peaks of the mid-span deflections of the simply supported double-beam system were divergent.The results suggested that under a large moving mass and at a high movement speed,inertial effect had a significant influence on the dynamic responses of the simply supported double-beam system.Therefore,excluding the influence of inertial effect would cause significant errors in the calculation results of the dynamic response of the simply supported double-beam system.

4.4 Effect of Winkler-layer spring stiffness and damping on the dynamic response of the simply supported double-beam system

In order to study the influence of Winkler-layer spring stiffness on the dynamic response of the simply supported double-beam system,after setting the spring stiffness values of various Winkler layers (i.e.,k1=1 .2 × 1 08N/m2,k2=3 × 108N/m2andk3= 6 × 1 08N/m2),the effect of Winkler-layer spring stiffness on the dynamic responses and impact coefficientIof the mid-span deflections when the mass movement speed increased from 0 to 200 m/s was analyzed,and the calculation results are shown in Fig.10 and Fig.11.WhereI= (Dd-Ds)/Ds,DdandDsrepresent the maximum dynamic mid-span deflection and static deflection,respectively.

Figure 10:Effects of Winkler-layer spring stiffness on the dynamic response of the simply supported double-beam system

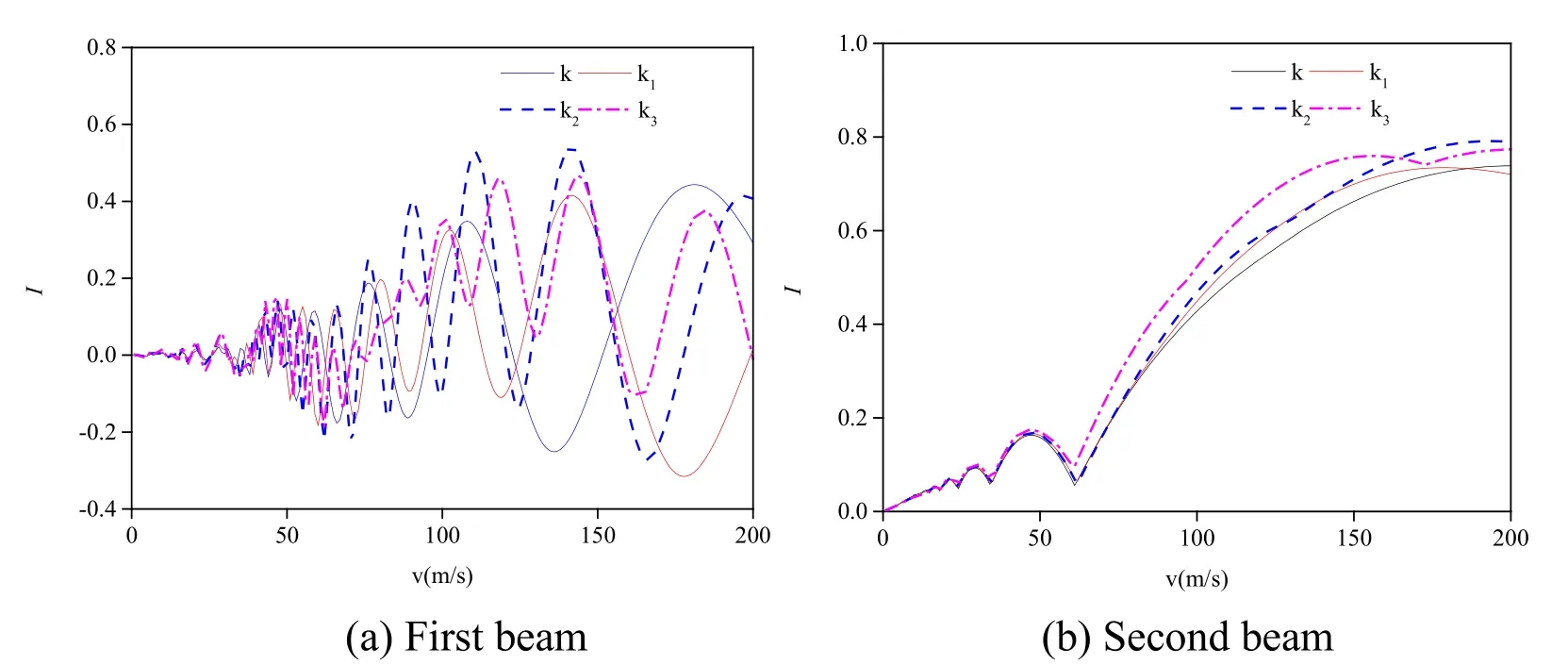
Figure 11:Effects of Winkler-layer spring stiffness on the impact coefficient of the simply supported double-beam system

In order to study the influence of Winkler-layer damping on the dynamic response of the simply supported double-beam system,the proposed analytical method was used to calculate the dynamic responses and impact coefficient of the mid-span deflections of the simply supported double-beam system when the mass movement speed increased from 0 to 200 m/s according to two circumstances,i.e.,with and without damping.The calculation results are shown in Fig.12 and Fig.13.

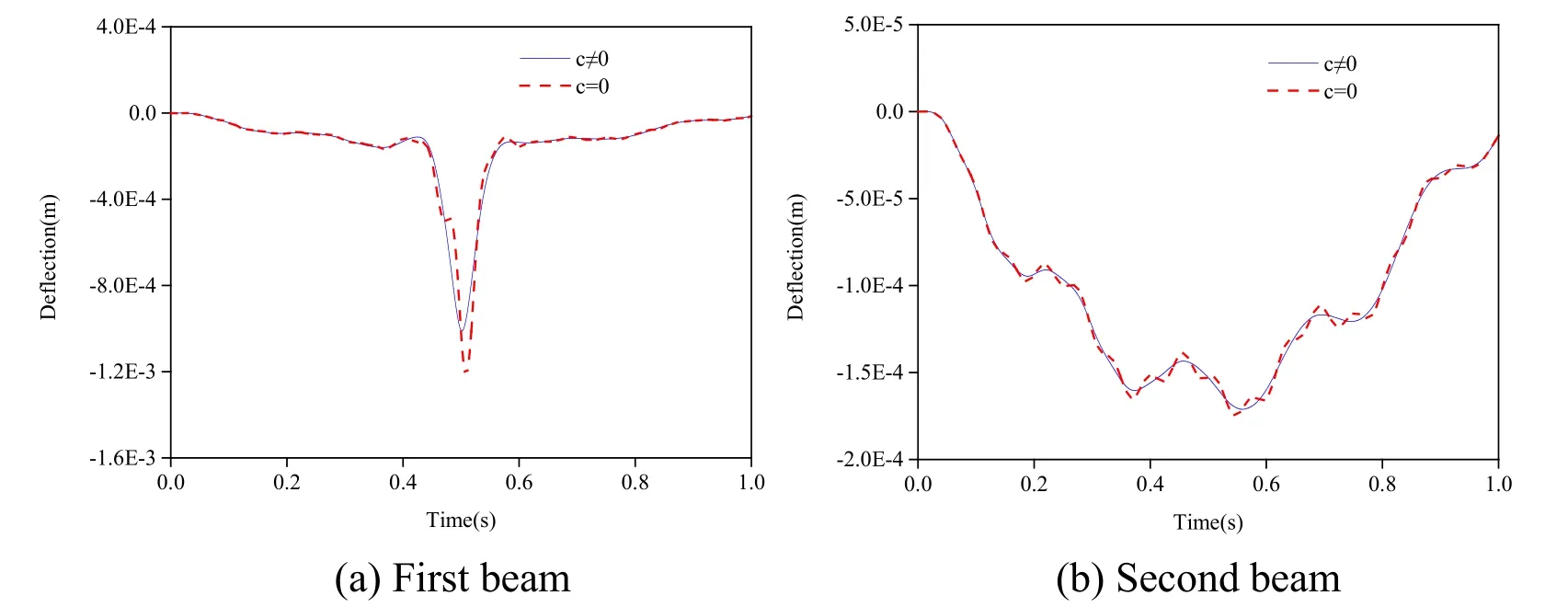
Figure12:Effects of Winkler-layer damping on the dynamic response of the simply supported double-beam system

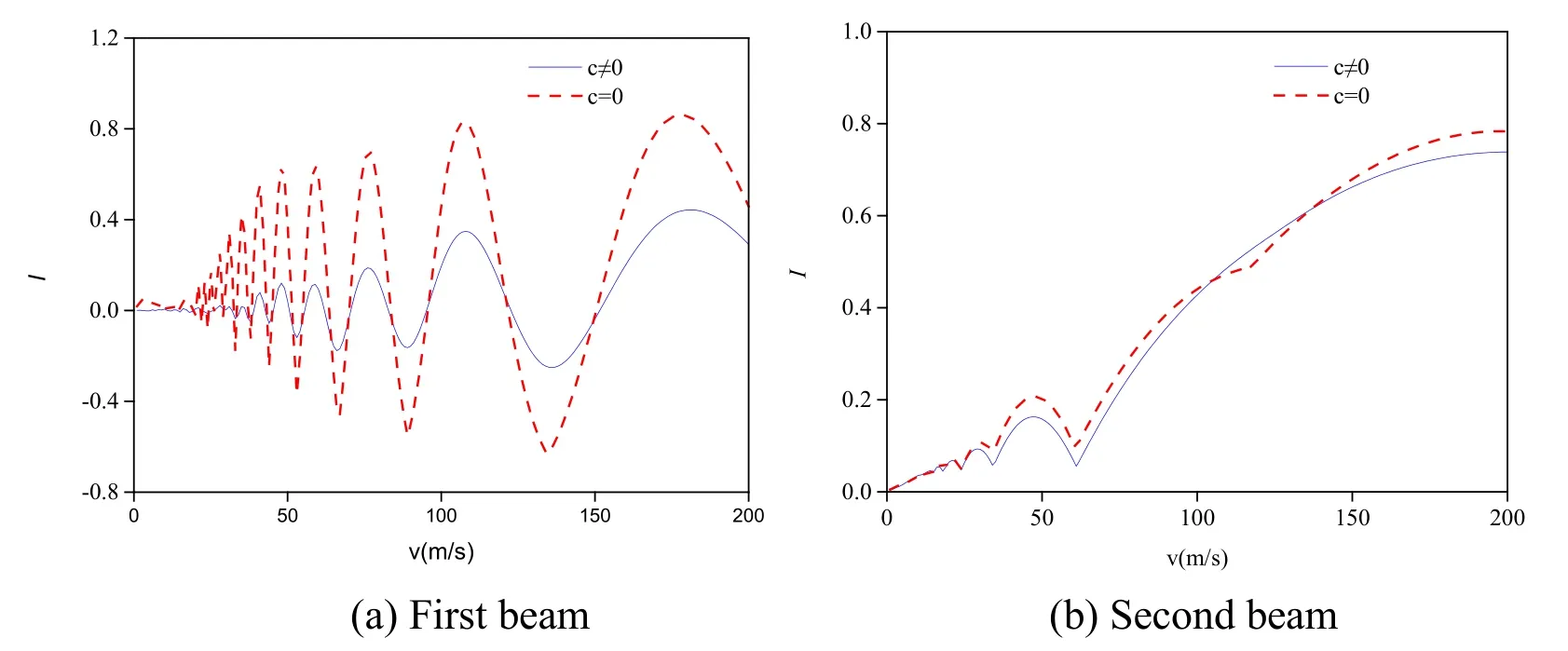
Figure 13:Effects of Winkler-layer damping on the impact coefficient of the simply supported double-beam system

According to Figs.10-13:When the mass movement speed increased from 0 to 200 m/s,its effect on impact coefficient was complicated.The impact coefficient-movement speed relationship curve of the first beam presented the form of a sine wave,and the amplitude of the sine wave increased with the movement speed increasing.The impact coefficientmovement speed relationship curve of the second beam presented the form of a half-sine wave,and its amplitude and period both increased with the movement speed increasing.This suggested that the movement speeds at which the moving mass caused the simply supported double-beam system to experience resonance were not continuous (i.e.,occurring at several speed points),and that the higher the mass movement speed,the higher the amplitude of the resonant dynamic response of the simply supported double-beam system.Winkler-layer spring stiffness showed a relatively small effect on both the midspan dynamic response and impact coefficient of the second beam,but its effect on the mid-span dynamic response and the impact coefficient of the first beam was uniformly significant.The amplitude of the resonant dynamic response of the first beam presented an increasing trend first and then decreasing afterwards with the Winkler-layer spring stiffness increasing.Thus,it is necessary to avoid sensitive Winkler-layer spring stiffness values to reduce the dynamic response of the first beam.In the presence of damping in the Winkler layer,the mid-span dynamic response and impact coefficient of the simply supported double-beam system were significantly smaller than those without damping in Winkler layer.Thus,increasing damping could effectively reduce the dynamic response of the simply supported double-beam system.

4.5 Effect of elastic moduli of the first beam and the second beam on the dynamic response of the simply supported double-beam system

In order to study the influence of elastic modulus of the first beam and the second beam on the dynamic response of the simply supported double-beam system,three cases of elastic moduli values of the first beam (E11=1.03 × 1011N/m2,E12=4.12 × 1 011N/m2andE13=1.03 × 1012N/m2)and three cases of elastic moduli values of the second beam (E21=1.725 ×1010N/m2,E22=6.9 × 1010N/m2andE23=1.725 ×1011N/m2)are chosen,and the effect of the elastic modulus values of the first beam and the second beam on the dynamic responses and the impact coefficient of the mid-span deflections of the simply supported double-beam system are analyzed when the mass movement speed increased from 0 to 200 m/s,and the calculation results are shown in Figs.14-17.

According to Figs.14-17:The elastic moduli of the first beam and the second beam exerted a significant influence on both the mid-span dynamic response and the impact coefficient of the first beam,and the mid-span dynamic response decreases with the increase of both the elastic modulus of the first beam and the second beam.The elastic modulus of the first beam exerted a relatively small effect on both the mid-span dynamic response and the impact coefficient of the second beam.However,the elastic modulus of the second beam exerted on the mid-span dynamic response and impact coefficient of the first beam was uniformly significant,and the mid-span dynamic response decreases with the increase of the elastic modulus of the second beam.Thus,increasing the elastic modulus of the second beam could effectively reduce the dynamic response of the simply supported double-beam system.

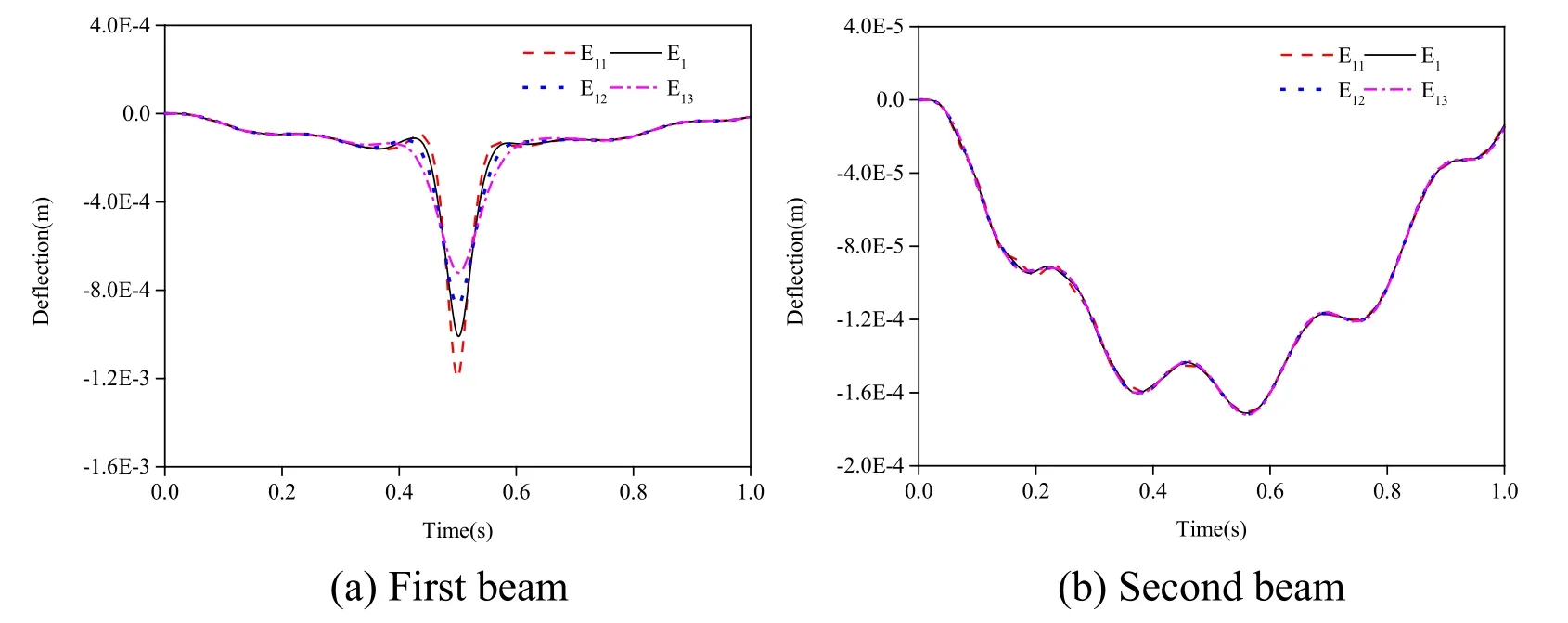
Figure 14:Effects of elastic modulus of the first beam on the dynamic response of the simply supported double-beam system

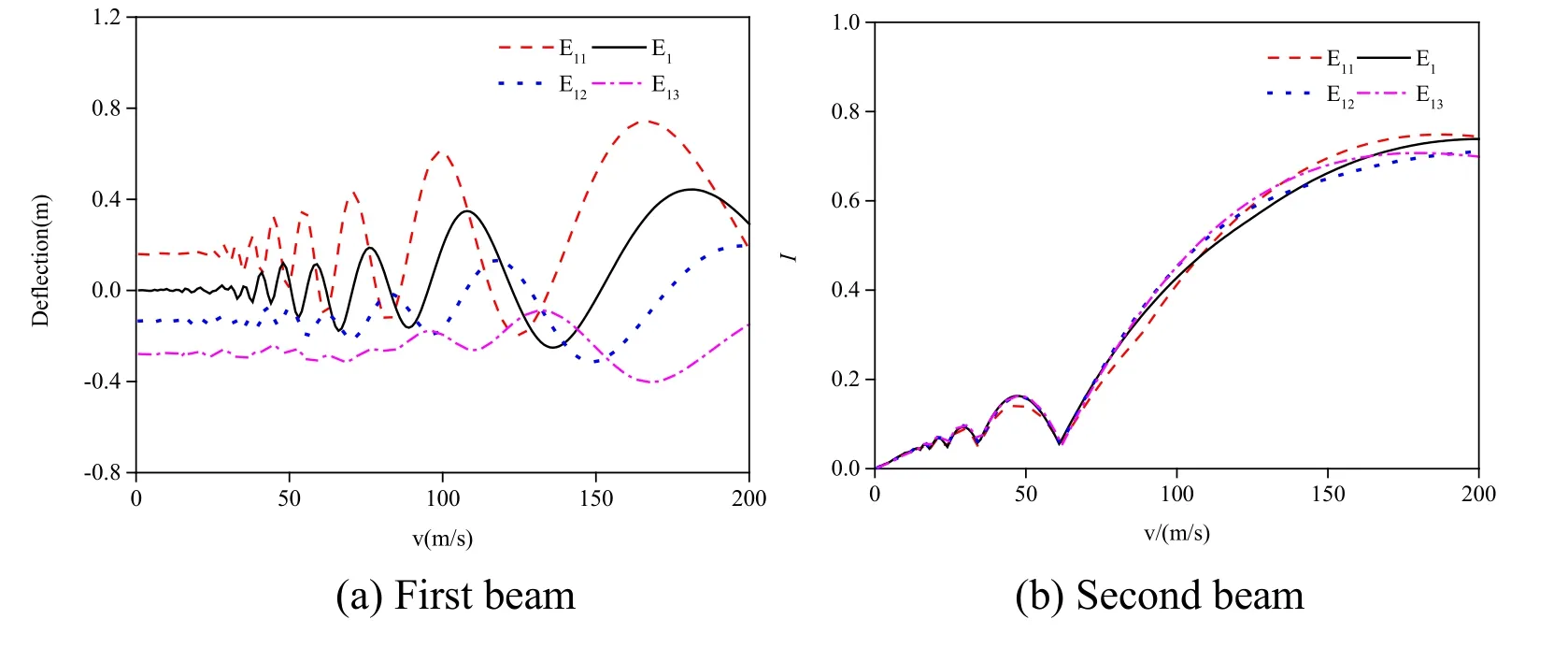
Figure 15:Effects of elastic modulus of the first beam on the impact coefficient of the simply supported double-beam system

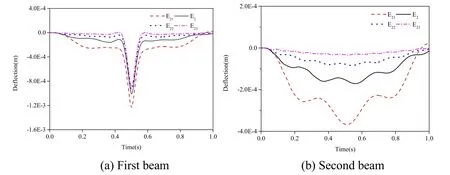
Figure 16:Effects of elastic modulus of the second beam on the dynamic response of the simply supported double-beam system

Figure 17:Effects of elastic modulus of the second beam on the impact coefficient of the simply supported double-beam system

5 Conclusions

Employing finite sin-Fourier Inverse Transform,the analytical solution for the dynamic response of the simply supported double-beam system under a moving mass was obtained.The dynamic responses of the simply supported double-beam system with different parameters were compared,and the main results were as follows:

(1)The analytical calculation results fit well with the ANSYS finite element numerical calculation results,demonstrating the effectiveness of the proposed analytical method.

(2)When the moving mass was small relative to the mass of the first beam,the inertial effect only has an insignificant influence on the dynamic responses of the mid-span deflections,and the influence of inertial effect on the dynamic responses cannot be ignored when the moving mass is large relative to the mass of the first beam.

(3)Under a large moving mass and at a high movement speed,the inertial effect has a significant influence on the dynamic responses of the simply supported double-beam system.Therefore,ignoring the inertial effect would cause significant errors in the calculation results of the dynamic response of the simply supported double-beam system.

(4)The simply supported double-beam system has several resonant speeds.The higher the mass movement speed,the higher the amplitude of the resonant dynamic response of the simply supported double-beam system would be.

(5)The effect of Winkler-layer spring stiffness and damping on the vibration of the second beam is not obvious,but its influence on the vibration of the first beam is significant.The Winkler-layer damping can effectively reduce the dynamic response of the double-layer simply supported beam.

(6)The mid-span dynamic response of the first beam decrease with the increase of the elastic modulus of the first beam and the second beam,but the mid-span dynamic response of the second beam decrease with the increase of the elastic modulus of the first beam and the second beam.

Acknowledgement:The research described in this paper was financially supported by the Fundamental Research Funds for the Central Universities of Central South University (2018zzts189),the National Natural Science Foundations of China (51778630).

Appendix A:Nomenclature

cWinkler-layer spring damping

E1Elastic moduli of the first beam

E2Elastic moduli of the second beam

{Fj} Vibration vector

I1Horizontal moments of inertia of the first beam

I2Horizontal moments of inertia of the second beam

kWinkler-layer spring stiffness

LLength of the beam

MSize of moving mass

m1Per-unit-length beam masses of the first beam

m2Per-unit-length beam masses of the second beam

NNumber of Fourier series

tTime

{Uj} Displacement vector

{} Speed vector

{} Accelerated speed vector

vLoad movement speed

y(x,t)1Deflections of the first beam

y(x,t)2Deflections of the second beam

δDirac function

η Generalized displacement vector

ΔtTime step

Appendix B：The detailed expression ofand