3-D Thermo-Stress Field in Laminated Cylindrical Shells
2019-11-26HaiQianSaiHuenLoDingZhouandYangYang
Hai Qian ,Sai-Huen Lo,Ding Zhou and Yang Yang
Abstract: The temperature and the stress distribution in simply-supported laminated cylindrical shells undergo thermal loads on the surface have been investigated.Exact solutions of physical quantities including temperature,heat flux,thermal displacement and stress are developed for the cylindrical laminated shell.Cylindrical shells are partitioned into more thin layers.In cylindrical coordinate,analytical expressions for physical quantities inside each layer are derived.Taking into account the compatibility of physical quantities at the interfaces,the relations between the outer and the inner layer of the laminated shell can be described with a transfer matrix.The undetermined parameters from the solutions of each layer can be obtained with boundary conditions.The convergence of the solutions to the number of Fourier series terms has been checked.The accuracy and feasibility of the present method is verified by comparing theoretical results with numerical outcomes due to Finite Element Method (FEM).Finally,the influences of surface temperature,geometrical size and material properties with respects to temperature,thermal stresses and displacement of layered cylindrical shell are worked out in details in a parameter study.
Keywords: Laminated cylindrical shells,thermo-elasticity,analytical solutions,transfer matrix.
1 Introduction
The mechanical responses of layered cylindrical shells have attracted considerable research efforts due to their increasing applications in the transportation of liquid and solid materials.Owing to the inhomogeneity of the laminated shell,complex stresses and deformations may be resulted even under a uniform temperature field.An accurate assessment of the displacement and the stress distribution in layered shell due to temperature loads would bring an important effect on the design and the structural safety of cylindrical pipes and other laminated composite cylindrical structures.
Lots of findings on temperature field of structural elements were presented before.Chang et al.[Chang,Kang and Chen (1973)] used Green’s formulas to study steady and transient heat transfer in porous materials.Marin et al.[Marin and Lesnic (2007)] investigated the problems of steady heat conduction around nonlinear functionally graded materials (FGMs).Norouzi et al.[Norouzi,Delouei and Seilsepour (2013)] obtained exact solution for steady-state heat transfer in the fiber reinforced composite multilayered materials.Kayhani et al.[Kayhani,Norouzi and Delouei (2012)] adopted Sturm-Liouville theorem to derive the exact solution to investigate steady heat conduction in laminated cylinder.Tarn et al.[Tarn and Wang (2003)] used the state space approach to study the problem of heat conduction in anisotropic tube made by functional gradient materials.LU factorization approach is used by Kayhani et al.[Kayhani,Shariati,Nourozi et al.(2009)] to get an explicit solution of the steady heat conduction for composite laminated cylinder.Based on an equivalent single layer method,Blanc et al.[Blanc and Touratier (2007)] adopted equivalent single layer method and obtained an advanced exact model to solve the heat conduction problems for laminated structures.Ma et al.[Ma and Chang (2004)] developed a refined approach to solve the problem of heat conduction for anisotropic laminates.Haji-Sheikh et al.[Haji-Sheikh,Beck and Agonafer (2003)] derived an analytical solution to investigate steady heat conduction in doublelayered objects.Rahideh et al.[Rahideh,Malekzadeh and Haghighi (2012)] simulated the heat conduction with finite wave heat speed in laminated FGM domain.
Thermal stresses on laminated structures have been widely studied by many researchers.Eason [Eason (1962)] studied time dependent thermal stress problems when the material is anisotropic.Ieşan [Ieşan (1980)] employed the linear thermo-elasticity theory and investigated the responses of laminated cylinder.Fard [Fard (2015)] showed exact analytical result to analyze a composite laminated panel under different boundary conditions according to an advanced sandwich panel theory.Aziz et al.[Aziz and Torabi (2013)] derived an exact solution of thermal stresses for hollow cylinder with constant interior heat generation and prescribed temperature conditions.Based on the thermoelastic theory,Ruhi et al.[Ruhi,Angoshtari and Naghdabadi (2005)] obtained an analytical solution of laminated cylinders made by functionally graded materials.Ma et al.[Ma,Dui,Yang et al.(2015)] studied thermal displacements and stress from a hollow FGM sphere subjected to uniform thermal load and present an analytical solution.Hyer et al.[Hyer and Cooper (1986)] derived an analytical solution to solve the problem of composite pips under surrounding temperature gradient.Hyer et al.[Hyer,Cooper and Cohen (1986)] studied the influences of a constant temperature change on deformations and stresses in composite pipes.For the Green-Lindsay type objects,Hetnarski et al.[Hetnarski and Ignaczak (1993)] investigated the thermo-elastic waves induced by instantaneous heating-source.Ghugal et al.[Ghugal and Kulkarni (2013)] studied thermal stresses and displacements for orthotropic cross-ply multilayered plates with the theory of trigonometric shear deformation.Huang et al.[Huang and Tauchert (1992)] investigated the static response of a double-curved cross-ply composite plate subjected to mechanical and thermal loads.Ali et al.[Ali,Alsubari and Aminanda (2016)] provided an improved theory of shear deformation to investigate a laminated shell under hygrothermal and mechanical loads through simplifying this problem to such case of generalized plane strain deformations.On basis of Donnell’s shell theory,Wu et al.[Wu,Jiang and Liu (2005)] studied the thermal buckling in multilayered shells made by FGMs.Javaheri et al.[Javaheri and Eslami (2002)] derived analytical solutions for the rectangular panel made by functional graded material subjected to thermal loads according to the classic plate theory.Alankaya et al.[Alankaya and Oktem (2016)] studied the problem of static analysis of cross-ply double-curved shell on basis of an improved shear deformation theory.Chen et al.[Chen and Liu (2001)] studied thermal stress of the thin laminates with a boundary element method.Najafizadeh et al.[Najafizadeh and Eslami (2002)] discussed thermal buckling of circle panel made by FGMs on basis of an advanced shear deformation plate theory.With an asymptotic approach,Reddy et al.[Reddy and Cheng (2001)] studied 3D deformations in simplysupported plane made by FGMs.Shiah et al.[Shiah,Guao and Tan (2005)] developed BEM to analyze the thermal effects in 2D anisotropic material with heat sources.Kim et al.[Kim,Zhou and Chattopadhyay (2002)] established the thermal-piezoelectricmechanical coupling model to study the distribution of interlaminar stress in smart laminated shells.Yas et al.[Yas and Aragh (2010)] discussed the 3D steady problem for the fiber rein-forced cylindrical panel made by FGMs.Kumar et al.[Kumar,Chakrabarti and Ketkar (2013)] provided static study of skew laminated shells with the theory of higher order shear deformation.Yuan [Yuan (1993)] provided an exact solution to discuss the thermal-induced responses of thick laminated shells under varying thermal load.Qian et al.[Qian,Zhou,Liu et al.(2014,2015)] derived analytical solutions for simply-supported laminated plane undergoing different thermal loads.Moreover,Qian et al.[Qian,Zhou,Liu et al.(2015)] studied the simply-supported composite arches under steady thermal loads.On basis of refined shear deformation theory,Alankaya et al.[Alankaya and Erdonmez (2017)] used Double Fourier series to study the effects of curvature on hyperbolic paraboloidal formed,multilayered composite surfaces.With Galerkin finite element method,Ahmadi [Ahmadi (2017)] present a layer wise solution to investigate the distribution of stress in laminated plate under prescribed mechanical loads.Sladek et al.[Sladek,Sladek,Solek et al.(2008)] analyzed the thermal stresses in the Reissner-Mindlin shells with a meshless local Petrov-Galerkin approach.Civalek et al.[Civalek (2007);Civalek (2008);Civalek (2017);Civalek and Acar (2007)] studied free vibration in the conical panel,isotropic conical shells,carbon nanotubes reinforced,FG shell and plates,Mindlin plates on elastic foundations by discrete singular convolution.Bishay et al.[Bishay,Sladek,Sladek et al.(2012)] explored a new finite element to study MEE materials.Akgöz et al.[Akgöz and Civalek (2011)] studied nonlinear free vibration about thin laminates supported by non-linear elastic foundations.Zuo et al.[Zuo,Yang,Chen et al.(2014)] used a wavelet finite element to analyze FG plates with the Mindlin plate theory.Baltacıoglu et al.[Baltacıoglu,Akgöz and Civalek (2010)] studied large deflection of laminated plates.Xiang et al.[Xiang,Ma,Kitiornchai et al.(2002)] studied vibration in thin cylinders supported by intermediate ring and obtained an exact solution.Talebitooti [Talebitooti (2013)] studied free vibration in composite conical shells with LW-DQM.Wu et al.[Wu and Chi (2004)] presented an asymptotic theory to study nonlinear problem in laminated cylinders based on 3D nonlinear elastic theory.Wu et al.[Wu,Chiu and Wang (2008)] analyzed simply supported laminated piezoelectric plates based on the RKP method.Heydarpour et al.[Heydarpour,Malekzadeh,Haghighi et al.(2012);Heydarpour,Malekzadeh and Gholipour (2019);Heydarpour and Malekzadeh (2019)] used Lord-Shulman theory to study thermoelastic behavior of multi-FG spherical shells and FG-GPLRC spherical shells,and analyzed thermoelastic response of rotating FG cylinders with layerwise differential quadrature method.Malekzadeh et al.[Malekzadeh and Ghaedsharaf (2014)] studied thermoelastic problem of laminated cylindrical panels according to 3D thermoelasticity theory.Malekzadeh et al.[Malekzadeh,Fiouz and Razi (2009)] presented a dynamic solution of laminated plates undergo moving load on the basis of 3D elasticity theory.Malekzadeh et al.[Malekzadeh and Beni (2015)] studied nonlinear free vibration of FG plates undergo different conditions.
Without the consideration of the effect of transverse shear deformation,the classic lamination theory with Love-Kirchhoff assumptions is a practical approach to assess the behavior of thin laminates.For thick laminates,the effect from transverse shear deformation should not be ignored.In this study,the 3D thermo-elasticity theory is applied to the laminated cylindrical shells under steady-state thermal loads on surfaces.The analytical solutions of each layer in laminated shells were developed with the help of transfer matrix method.Unlike one-layer equivalent approach,each layer of different material properties is dealt with separately,such that displacement and stresses at the interface are strictly compatible.
2 Temperature distributions over the cylinder
2.1 Temperature in a single shell layer
A laminated cylindrical shell consisted ofPlayers and the radius of the outer surface injth layer isrj(j=1,2...P).The materials of each layer are isotropic.The geometry and the cylindrical coordinate system of the shell are presented in Fig.1.The total length and the inner radius are represented bylandr0,respectively.The material of each laminated layer is isotropic with possibly district to each other.The case is considered that the temperature of the two ends is a constant and this value is taken as the reference temperature.Without loss of generality,the temperatures are furtherly considered to be zero based on the relative temperature concept.The shell is simple-supported on boundaries.The inner and the outer surfaces are under thermal loadst1(θ,z)andtp(θ,z),respectively.Besides,we assume that the properties of materials are uninfluenced by the thermal process experienced by the shell.
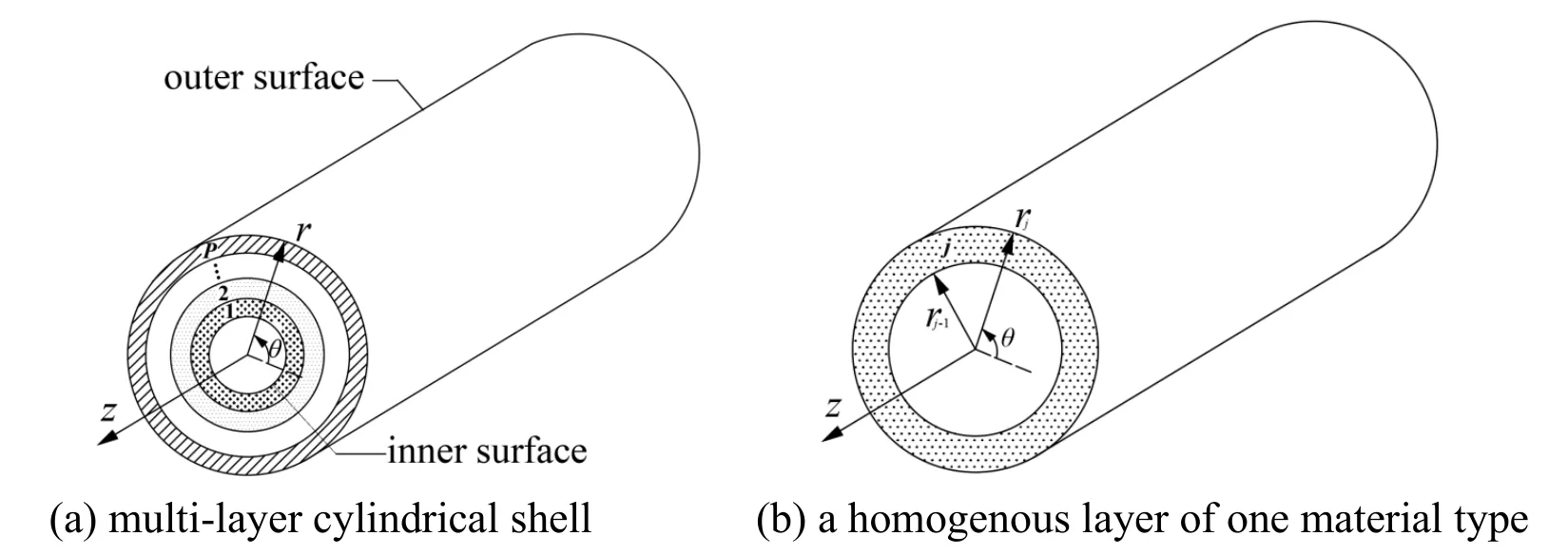
Figure 1:Model of multi-layer cylindrical shell
The thinning layer approach is introduced to solve the heat governing equation.As a result,each isotropic layer is further divided intoMj(j=1,2…P)layers.Thus,the total layer-number isNIn such case,the variablerin the heat governing equation can be approximately replaced by the center coordinate of layerri0.For thin layers,the heat conduction equation in theith (i=1,2 …N)layer can be given as
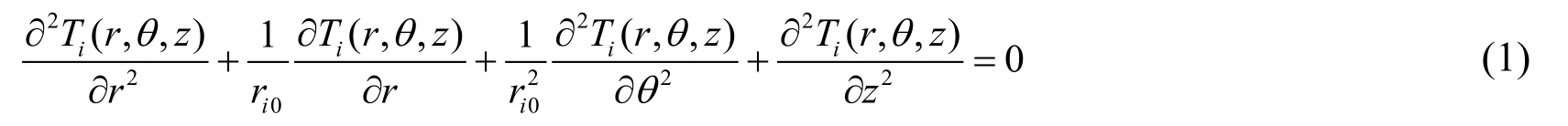
whereri0is the center coordinate of theith thin layer.
The temperature condition on the edges is

The temperature distributionTi(r,θ,z)can be given by the Fourier series

The temperature solution (3)satisfies the temperature conditions (2).Substituting Eq.(3)into Eq.(1),Ti(r,θ,z)can be worked out as follows,
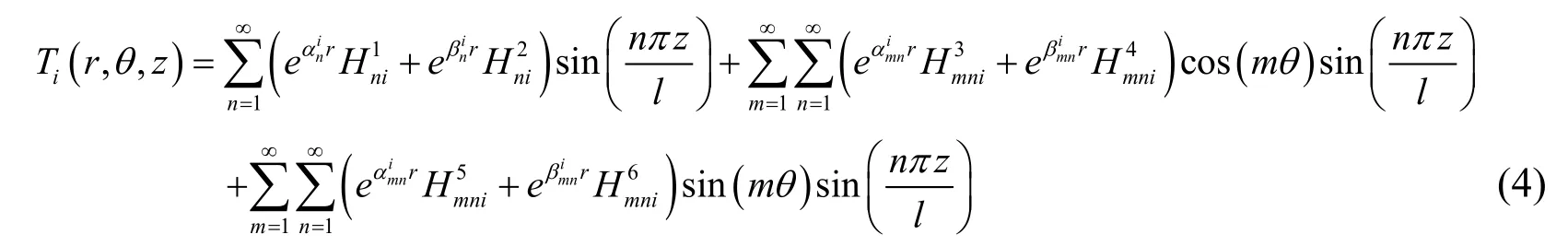
where,
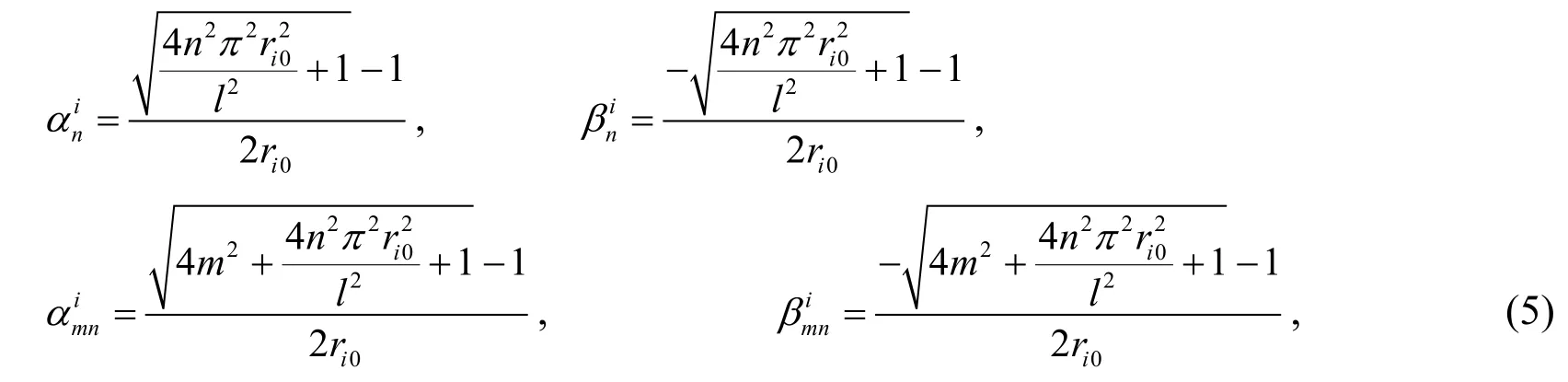
2.2 Induction formulae of temperature
Based on Eq.(4),we can rewrite the temperature and the heat flux as matrix,i.e.,
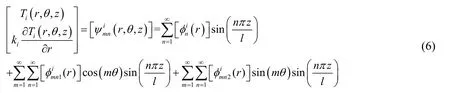
wherekiis heat transfer coefficient,andare 2×1 matrix function described as from temperature solution (4),
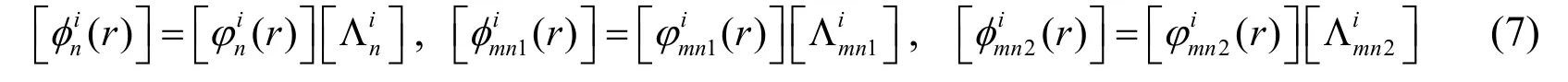
respectively,
in which,
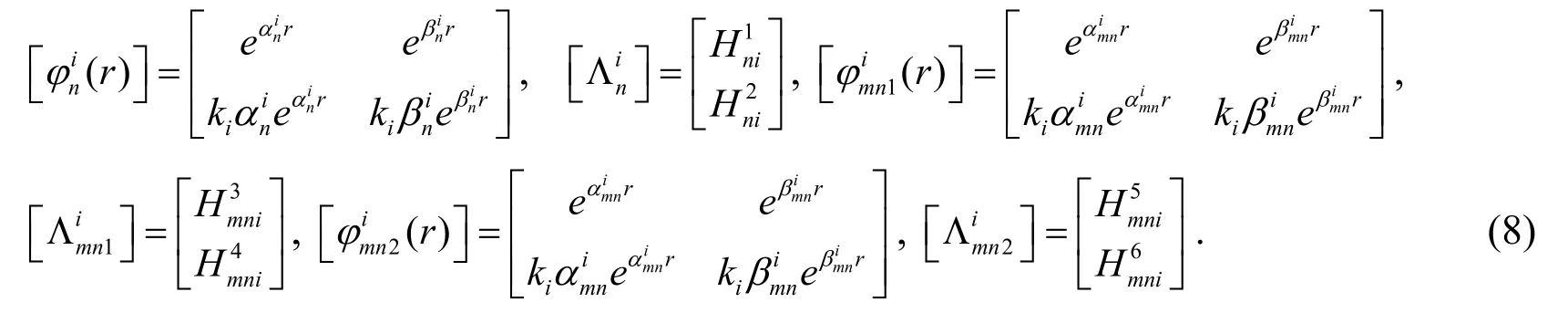
Takingr=riandr=ri-1in Eq.(7)respectively,the unknown coefficientsandcan be eliminated as follows,
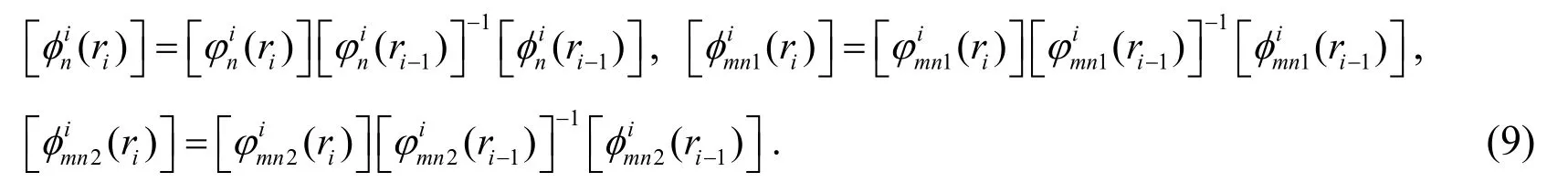
Based on the continuity condition at the interface of the laminated shell,we have

Therefore,the relations between theqth (q=2,3…N)and the inner layers can be recursively obtained:
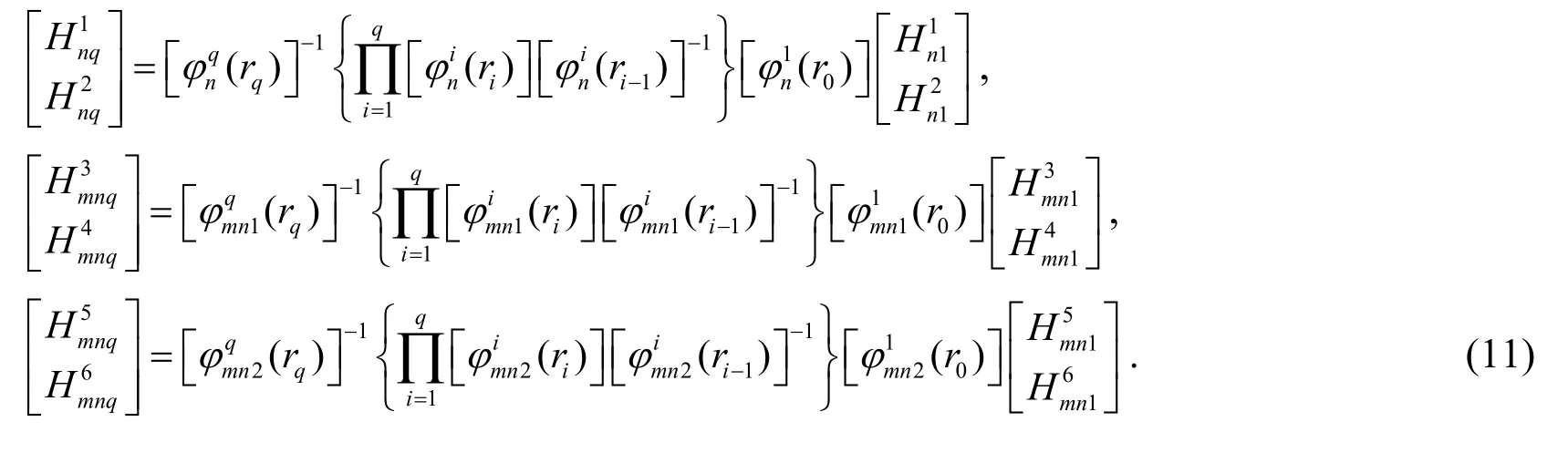
2.3 Undetermined temperature coefficients
Think over that outer and inner surfaces of cylindrical shell under steady state thermal loadstp(θ,z)andt1(θ,z),

The Fourier series can be adopted to express temperature loadstp(θ,z)andt1(θ,z),
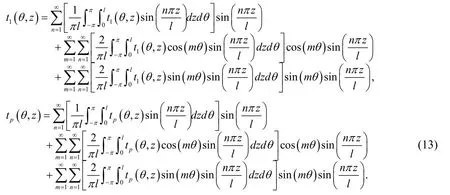
Substituting the temperature solution (4)into boundary Eqs.(12)and (13)gives

Solving Eq.(11)(takingq=N)and Eq.(14),andcan all be determined.Substituting the coefficients of the first layerback to Eq.(11),the unknown coefficients of theqth layer(q=2,3…N-1)can be determined in turn.At last,the temperature distribution can be derived out by taking these coefficients to the general solution of temperature field (4).
3 Displacement and stress distributions over the cylinder
3.1 Displacement in a single layer
The thermal expansion coefficient is denoted byαi.The Young’s modulus of each layer is denoted byEi.The Poisson's ratio is denoted byμi.The thinning layer approach in Section 2.1 can also be employed in simplifying the three-dimensional thermo-elasticity equation.Thermo-elastic constitutive relationships of theith layer (i=1,2 …N)in the cylindrical coordinate system are given by
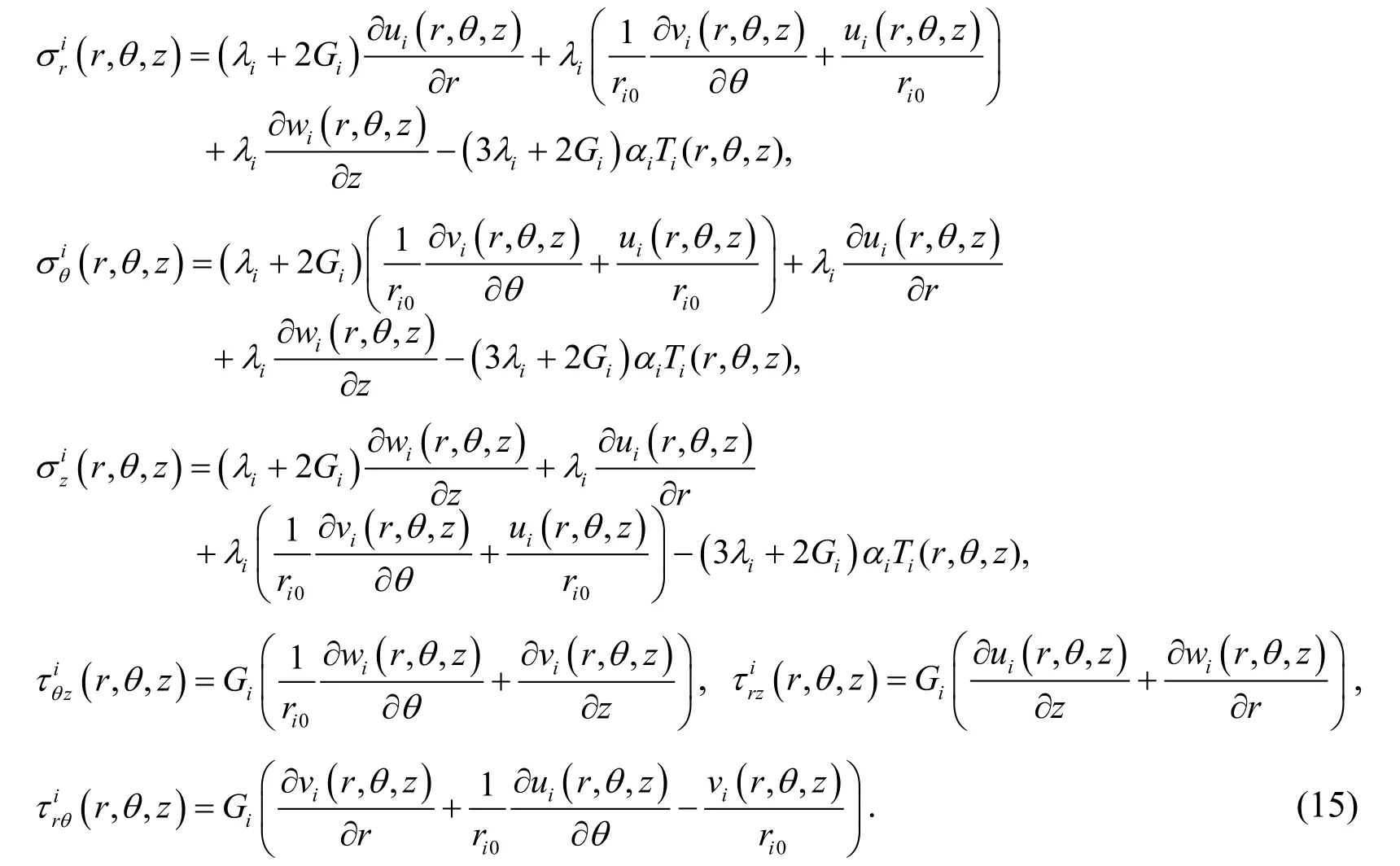

The equilibrium equations without the body forces for theith layer (i=1,2,…N)can be written as
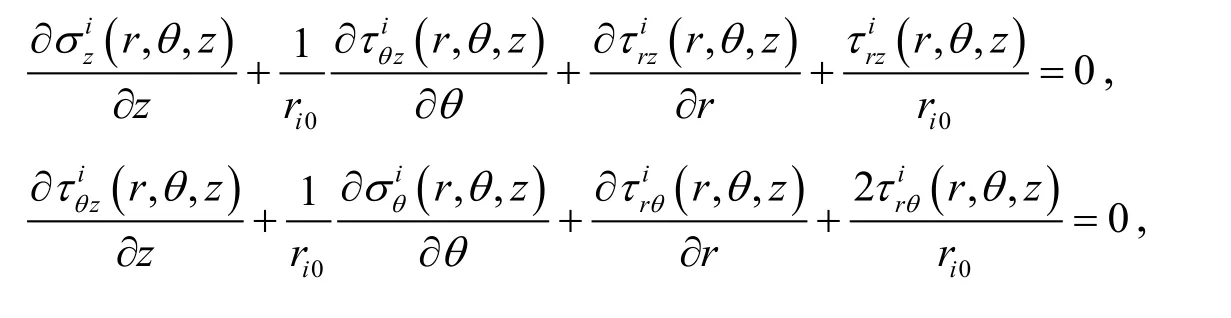
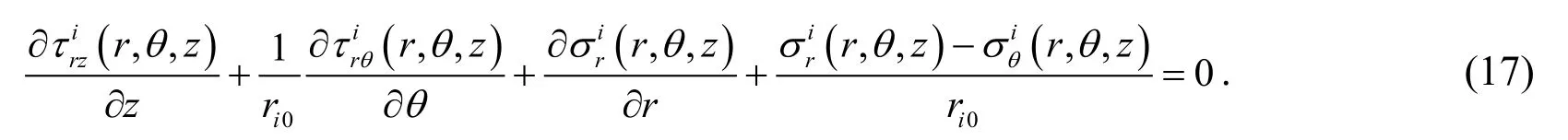
Substituting thermo-elastic constitutive relationships (15)into Eq.(17),the equilibrium differential equations for displacements are given by

Since there is no in-plane displacement on both ends,we can obtain

The Fourier series can be adopted to describe the displacement as follows,
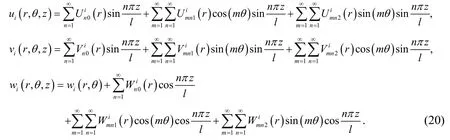
3.1.1 Case 1:n=0
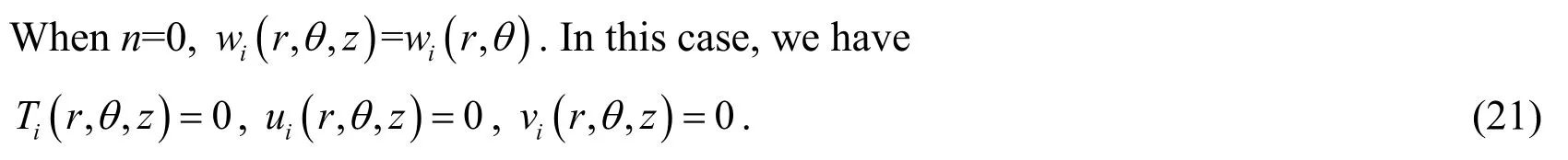
Substituting solution (21)into the equilibrium differential Eq.(18),a partial differential equation of second order is obtained:
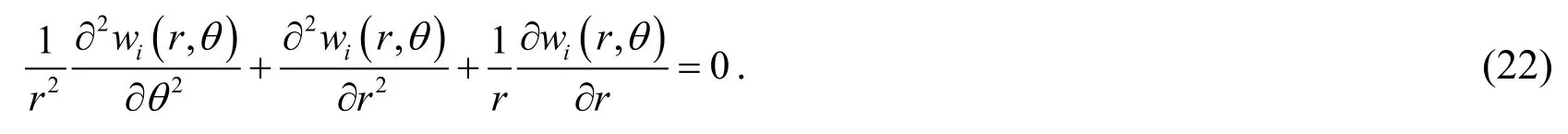
According to Eq.(22),the solution ofwi(r,θ)can be given by
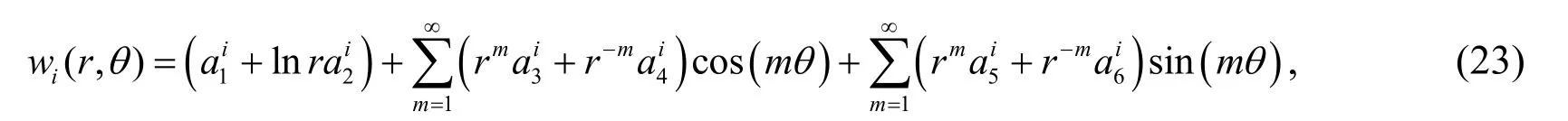
wherea1i,a2i,a3i,a4i,a5ianda6iare the coefficients determined from boundary conditions.
3.1.2 Case 2:n>0
Whenn>0,expressions of temperature (4)and displacement (20)are substituted into Eq.(18).The solutions ofui(r,θ,z),vi(r,θ,z)andwi(r,θ,z)are derived out as:

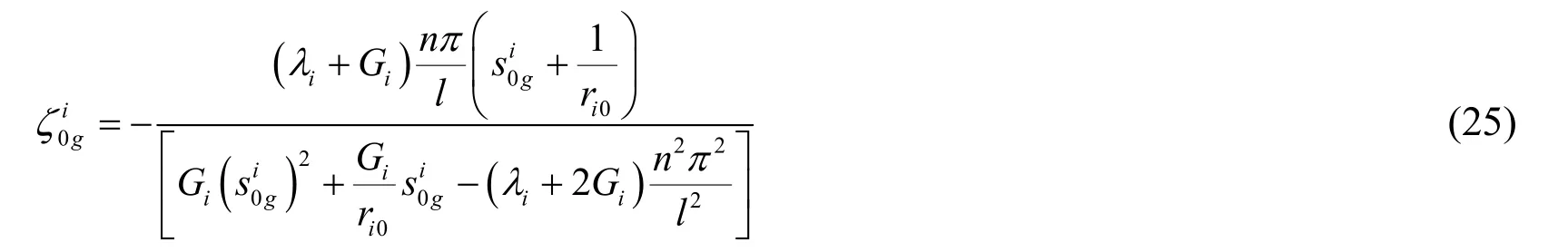
where,are the results of the equation:
and
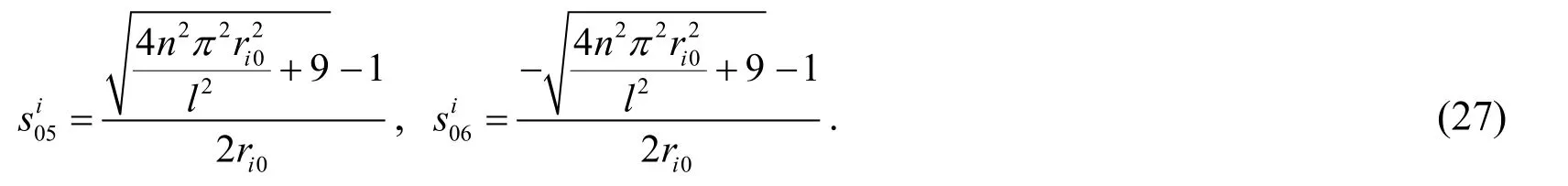
The second group of coefficients,and(g=1,2,3,4,5,6)can be obtained.is the roots of the following equation,
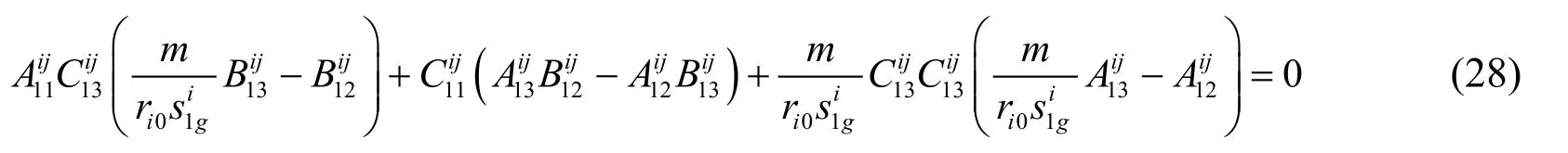
and

where,
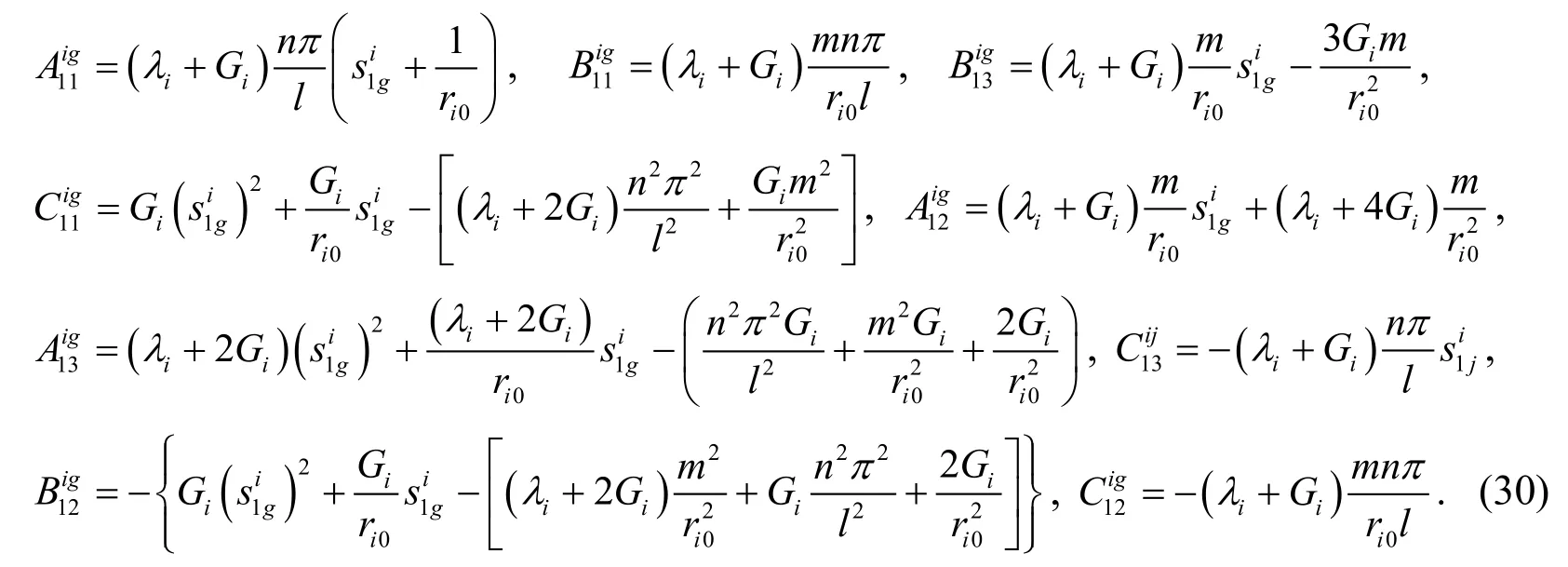
The third group of coefficientscan be obtained.is the roots of the following equation,
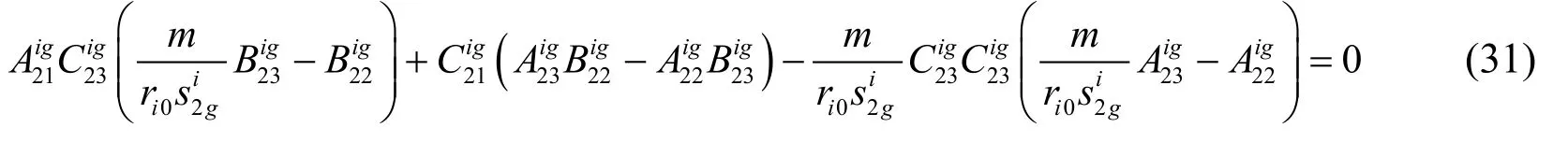
and

where,

Aswi(r,θ,z)≠ 0 forn=0,the complete solutions for displacements are the combining Eqs.(23)and (24)
3.2 Stresses in a single layer
Take the solutions of displacement to equation (15),the complete stress components are given by



3.3 Induction formulas of displacement and stress
The induction formulas are divided into two parts based on solutions of displacement and stress for case 1:n=0 and case 2:n>0.
3.3.1 Case 1:n=0
Whenn=0,the displacements and stresses as given in Eqs.(23)and (34)can be shortened as:
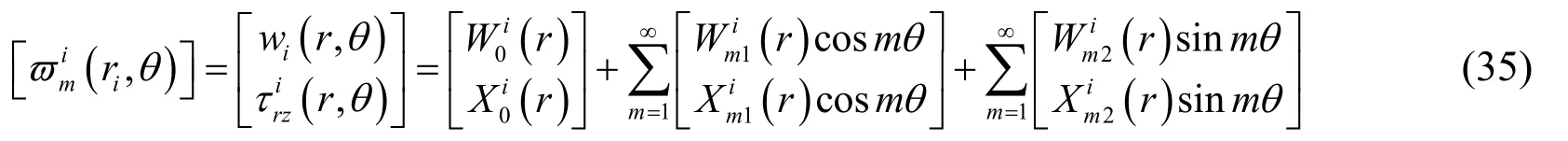
where,andare defined as the displacement functions,,andare stress functions.
For brevity,Eqs.(23),(34)and (35)can be rewritten as
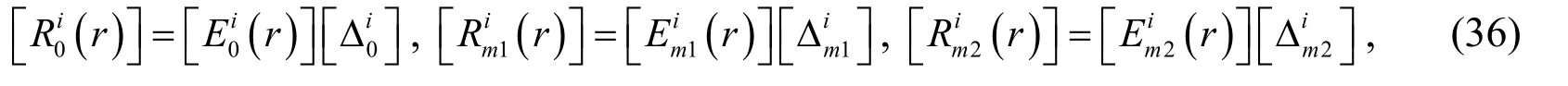
in which,

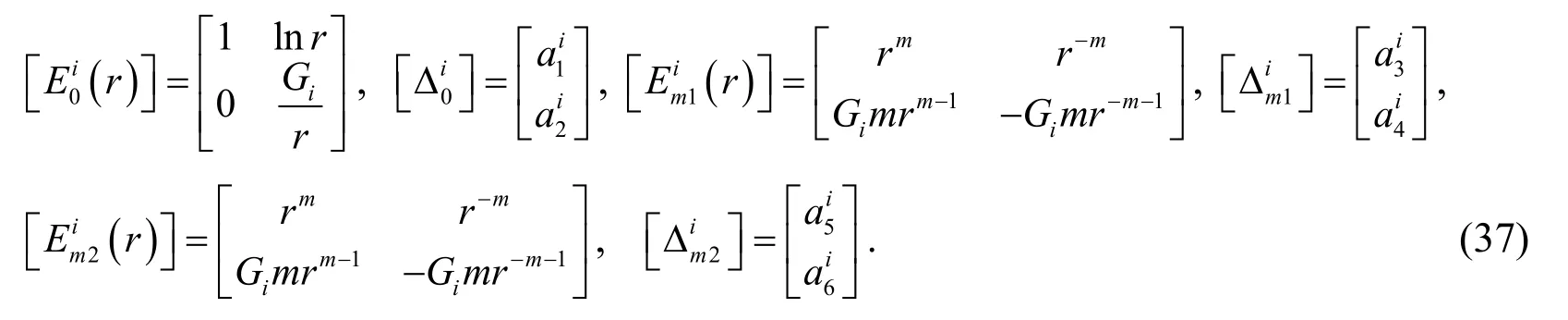
On basis of the continuities of physical quantities on the interface,we have

Thus,the relationships of physical quantities betweenqth and the innermost layers are given by:

3.3.2 Case 2:n>0
Whenn>0,the displacements and stresses of an isotropic layer as given in Eqs.(28)and (39)can be shortly rewritten as:
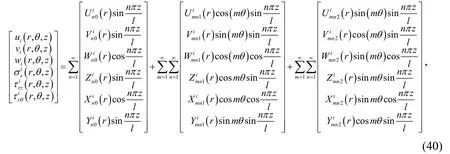
For brevity,Eqs.(24),(34)and (40)can be expressed as
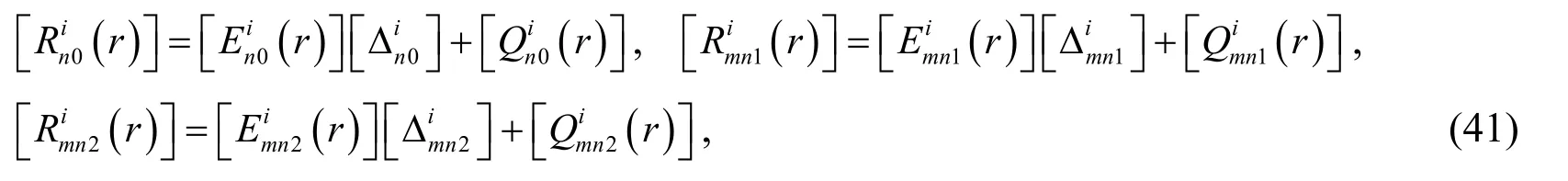
On basis of the compatibility of physical quantities at the interface,the relationships betweenqth (q=2,3,…,N)and innermost layers are given by:
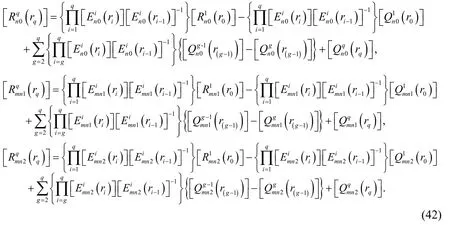
3.4 Coefficients of displacement and stress
In this analysis,the mechanical loads are not considered.If existed,the superposition method is adopted.The temperature conditions of cylindrical shells are
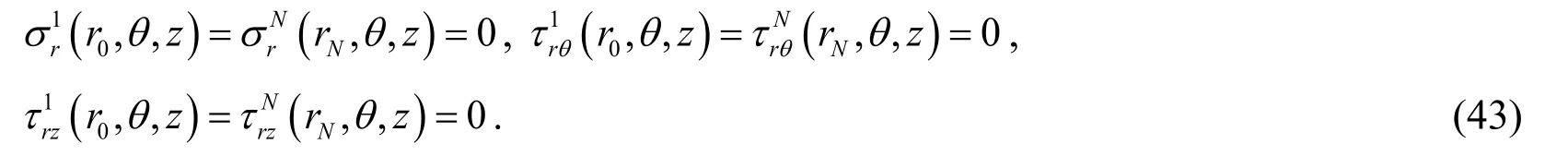
The two casesn=0 andn>0 are identified and are considered separately.
3.4.1 Case 1:n=0
Whenn=0,substituting Eq.(43)into Eq.(39)(takingq=N),the relationships of physical quantities between outer and inner layers are given by
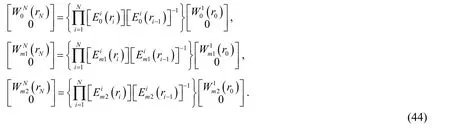
3.4.2 Case 2:n>0
Whenn>0,substituting Eq.(43)into Eq.(42)(takingq=N),the relationships of physical quantities betweenNth and innermost layers are
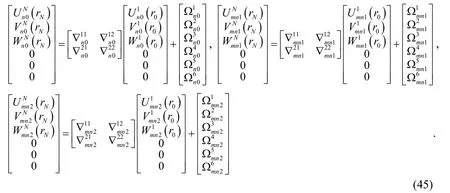
The detail of each matrix and abbreviations in Eq.(45)is given in Appendix B.
4 Convergence and comparison
A numerical example has been implemented to investigate the convergence ability of the present method.The double precision computations are conducted in the following numerical calculations.As the most common laminated structure in engineering practice,a triple-layer cylindrical shell is present as instance.The materials of surface layers and middle layer are steel and concrete,respectively,and their radii arer0=1.5 m,r1=1.9 m,r2=2.3 m,r3=2.7 m.The shell length isl=10 m.Poisson’s ratios of steel and concrete are 0.3 and 0.2,respectively.The thermal conductivities of steel and concrete are 50 W/(m·oC)and 2 W/(m·oC),respectively.The Young’s Moduli of steel and concrete are 200GPa and 30GPa,respectively.Thermal expansion coefficients of steel and concrete are 1.2×10-5/℃ and 0.7×10-5/℃,respectively.The inner surface of the cylindrical shell undergoes a uniform steady-state thermal load:t1(θ,z)=0℃,meanwhile the outer surface undergoes the thermal load:

where,t0=100oC.
The laminated shell is divided into 15 thin layers.Limiting indicesmandnin the infinite series toLin Eqs.(6),(25),(26)and (36),we have approximate results of displacement and stress in terms ofL.Five different numbers forL=15,20,25,30,35 have been checked in the series.Tab.1 provides the numerical results atr=1.6 m,θ=1.8 rad,z=4.2 m andr=2.0 m,θ=1.28 rad,z=3.2 m,respectively.Tab.1 reflects that the data converge rapidly with the growing numbers of termL.There is little difference between solutions forL=30 and 35.Thus,the terms’ number of Fourier series is set asL=30 in the subsequent calculations.

Table 1:Investigation of convergence
To evaluate the errors in adopting the thin layer approach in Eq.(2),the three-layer shell has been further divided progressively into 6,9,12,15 and 18 thin layers.Tab.2 presents the numerical results for displacements and stresses atr=1.6m,θ=1.8 rad,z=4.2 m andr=2.0 m,θ=1.28 rad,z=3.2 m,respectively.It is clear that the data forN=15 and 18 have identical three significant figures.This means we can eliminate the error through enlarging the number of the thin layers (i.e.,decreasing the thickness of thin layers).A finite element (FE)simulation with the help of ANSYS software (Element types:solid 90 for temperature analysis,solid 186 for structural analysis)has been implemented to assure the validity of the current method.The comparison of results at the five locations is given in Tab.3,which suggests that the FEM simulation results agree well with the analytical solutions.

Table 2:The influence of total thinning layer numbers
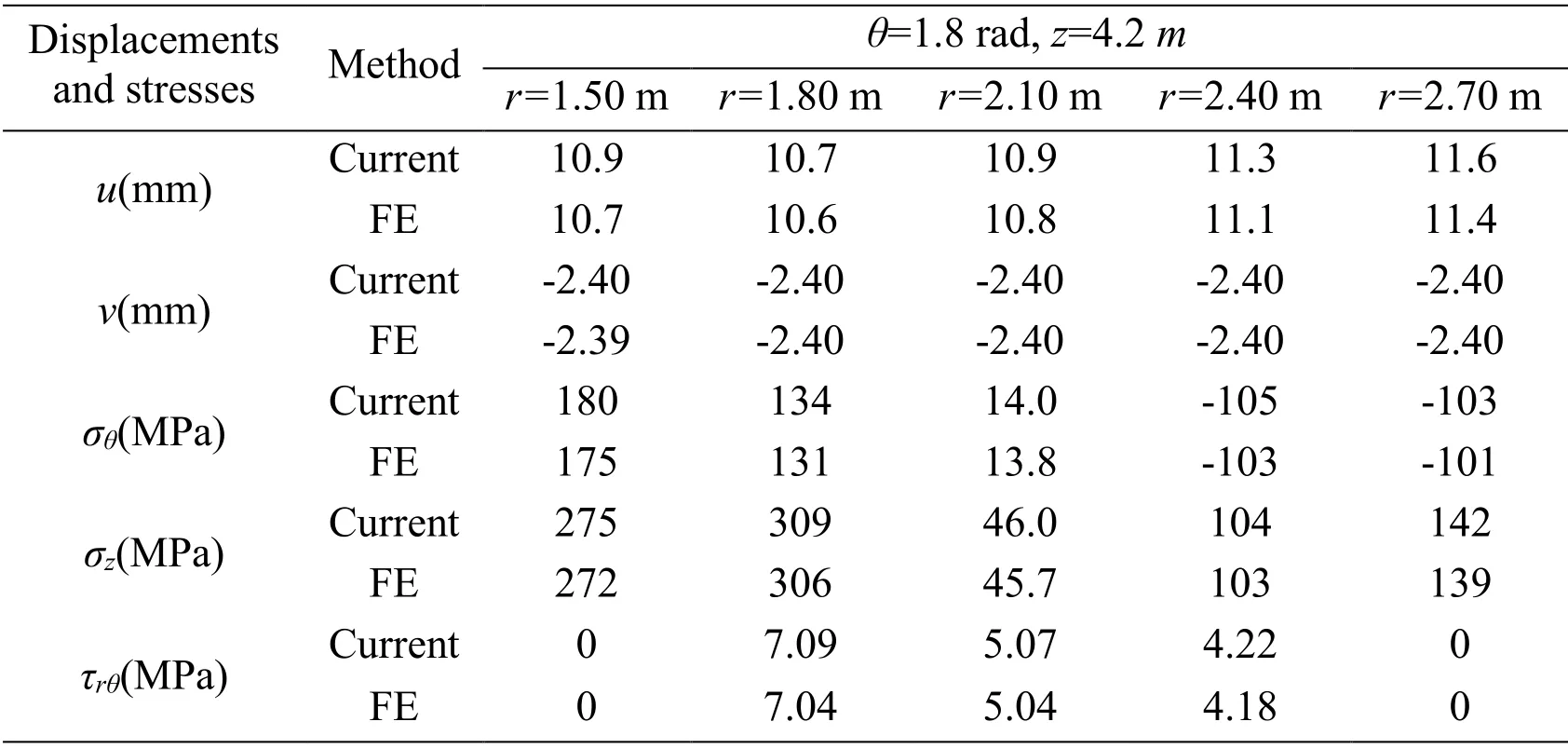
Table 3:Comparison studies towards current results and FE results
Numerical data are compared with the results from Ayoubi et al.[Ayoubi and Alibeigloo (2017)] to validate the present method.The hollow cylinder in reference is an isotropicone-walled functionally graded materials cylindrical shell with the dimensions ofr0=0.95 m,rp=1.05m,l=3 m.The surface temperatures aret1(θ,z)=200K andtp(θ,z)=0,respectively.The outer surface is metal (Ni)with the material propertieskm=90.5 W/(m·K),Em=206 GPa andαm=1.33×10-5/K.The inner surface is ceramic (SiC)with the material propertieskc=65 W/(m·K),Ec=427 GPa andαc=4.3×10-6/K.The material properties of the cylinder follow the laws:
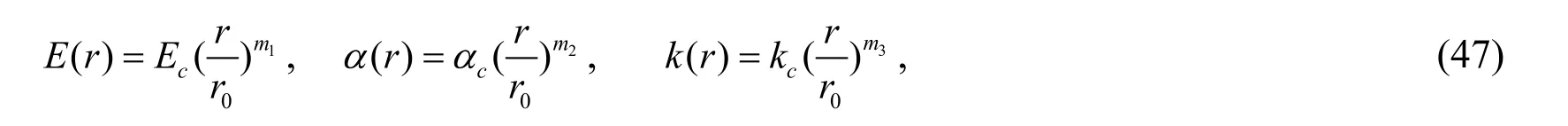
The functionally graded cylinder is divided into ten layers and the nondimensional stressσr*along the thickness atz=1.5 m can be obtained in Tab.4.From comparison of the present results with the reference,good agreement is found.

Table 4:Comparison of radial stresses σr* through the thickness with reference
5 Parameter studies
In this part,the discussion of temperature,displacement and stress mainly is focused on the influences of surface temperaturet0,geometric dimensions,the number of laminated layers and the material properties.
5.1 Influence of surface temperatures
The first model is a triple-layered cylindrical shell.The layer radii arer0=1.5 m,r1=1.9 m,r2=2.3 m,r3=2.7 m,respectively.The shell length isl=10 m.The material properties are identical with that shell shown in Section 4.The outer surface of the shell undergoes three different thermal loadst0:50oC,100oC,150oC in Eq.(46).The temperature of the inner surface is constant as 0oC.
Fig.2 illustrates the temperature change along therdirection atθ=1.8 rad,z=4.2 m for various temperature fields.It follows that the temperature variation rate within the surface layers along therdirection are pretty small in Fig.2.However,the temperature gradient within the middle layer is larger because the thermal conductivity of the surface layers in the cylindrical shell is much greater than that of the core layer.Fig.3 reflects the distributions ofu,v,σrandτθz.We can find from Figs.2 and 3 that the absolute values of all physical quantities increase with the increasing thermal loadst0from the outer surface.It is clear from Figs.3(a)and 3(b)that theuandvvary slightly withrbut increase with the increasing thermal load.Fig.3(c)presents thatσris always positive.Moreover,we can see from Fig.3(d)thatτθzare of discontinuity on the interfaces,i.e.,differentτθzexist for distinct material properties on two sides in the shell.
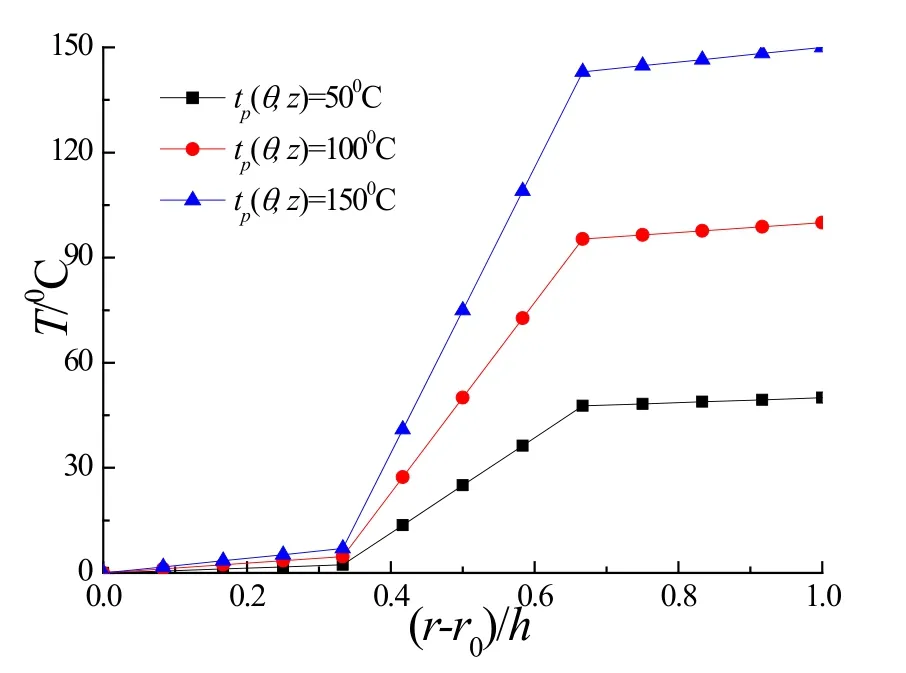
Figure 2:The temperature change along r-axis at θ=1.8 rad,z=4.2 m for a 3-layered cylindrical shell under different surface temperatures
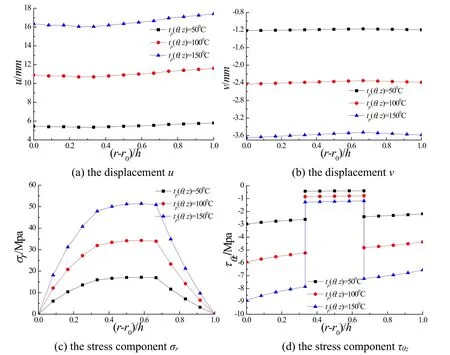
Figure 3:Displacements and stresses at θ=1.8 rad,z=4.2 m under different thermal loads
To analyze the stress distribution features on the interface,the distributions of stressesσθandτθzon two sides of the interface atr=1.9 m,z=4.25 m along theθdirection are depicted in Fig.4 fort0=100oC.Since the Young’s modulus of steel is relatively greater,we can see that the absolute values of stresses in surface layers are greater than those in middle layer at all time.
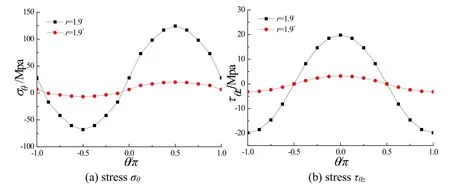
Figure 4:The σθ and τθz distribution for t0=100oC at r=1.9 m,z=4.25 m
5.2 Figures influence of the ratio h/r0
A three-layered cylindrical shell with thicknessh(i.e.,r3-r0)=1.2 m andh1=h2=h3=0.4 m is studied in this part.We considered three different valuesr0=1 m,1.5 m and 3 m,for whichh/r0=1.20,0.80 and 0.40 respectively.The shell length isl=10 m.The material properties of laminated shells are the same as given in Section 4.The outer surface in the cylindrical shell undergoes thermal loadt0=100oC in Eq.(46).The inner surface undergoes a constant thermal loadt1(θ,z)=0oC.
The temperature distribution along the radial directionratθ=1.8 rad,z=4.2 m is plotted in Fig.5,and Fig.6 presents the changes ofu,v,σrandσz.Fig.5 illustrates that the temperature distribution is almost constant with different ratioh/r0.Figs.6(a)and 6(b)reflect that absolute values for displacementsuandvincrease with increasingh/r0.Fig.6(c)tells that the change rates ofσrandσzincrease with the increasingh/r0.
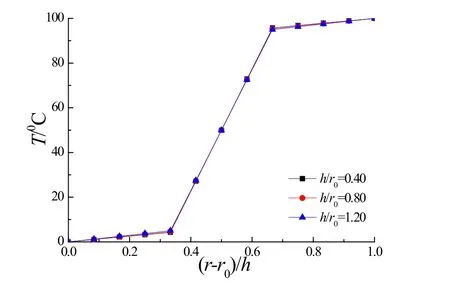
Figure 5:The temperature change at θ=1.8 rad,z=4.2 m along r-axis under different h/r0

Figure 6:Physical quantities at the r-axis at θ=1.8 rad,z=4.2 m under different h/r0
5.3 Influence of material properties
The last model is to compare the displacement and the stress along ther-axis of three distinct two-layered shells.The material of the inner layer is steel,while the material of the outer layer is concrete.The inner dimension of the tube isr0=2 m,and the outer dimension isr2=3.2 m.Hence the thicknesshof the tube equal to 1.2 m.All shells have the same lengthl=10 m.We considered three different thicknesses for the steel layerhs=0.4 m,0.6 m and 0.8 m for whichhs/hc=2.0,1.0 and 0.5 respectively.The outer surface in the layered shells undergoes a distributed thermal load witht0=100oC in Eq.(46).The inner surface is suffered a constant temperaturet1(θ,z)=20oC.The distributions ofT,v,w,σzandτrzatθ=π/4,z=4.5 m along the radial direction are given in Fig.7 and Fig.8.For cylindrical shells of the same total thickness,we can find temperature filed,thermal stresses and displacements are different.Fig.7 reflects that the temperatureTvaries lightly in steel layer,as thermal conductivity of steel is greater than concrete.Figs.8(a)and 8(b)clearly present that the displacementvandwchange substantially in the shell ofhs=0.4 m.The reason is that the Young’s modulus for steel is significantly greater than concrete.We can also observe from Fig.8(c)that the change ofσzon the interface between steel and concrete layers increases with decreasing ratiohs/hc.As shown in Fig.8(d)τrzis almost invariant near the inner surface,however,τrzchanges quite substantially in place away from the inner surface,say (r-r0)/h> 0.2 .
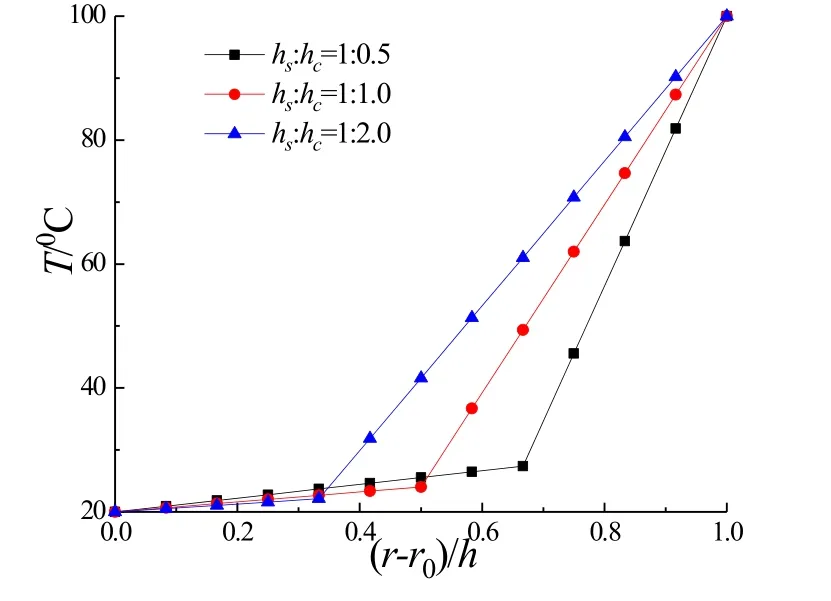
Figure 7:The temperature change at θ=π/4 rad,z=4.5 m along r-axis to different laminates

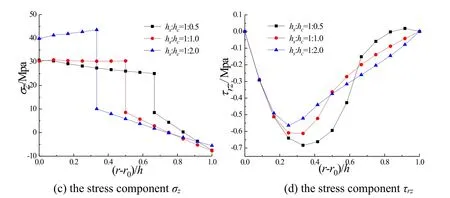
Figure 8:Displacement and stress distribution at θ=π/4 rad,z=4.5 m along r-axis under different laminates
6 Conclusions
This study presents an investigation into simply-supported layered cylindrical shells subjected to thermal loads on the surface on basis of the theory of exact threedimensional thermo-elasticity.With the consideration of the effect of transverse shear deformation and the continuities at the interface,the exact temperature and stress solutions can be readily derived by solving several sets of algebraic equations for laminated cylinders with arbitrary layers.Main conclusions are summarized as listed:
(1)By use of the theoretical method developed in this paper,the temperature distribution,displacement and stress of cylindrical layered shells under thermal loads can be derived in a straightforward way.
(2)A thinning layer approach is explored to solve the heat conduction equation and the three-dimensional thermo-elasticity equation.The results of FEM simulation are presented to compare with results due to the analytical method.The comparison of results suggests the accuracy and correctness of the present methodology.Also,the convergence property of the proposed method is examined and an excellent convergence property of the present approach is found.The present methodology can be used to study the thermal buckling problems.
(3)Results showed that the research objects in the shell consistently grow with the increasing thermal load on the outer surface.Stressσθandτθzare of discontinuity on the interfaces,i.e.,distinct material properties exist on two sides in the shell.The geometrical sizes and the material properties make significant influences on the temperature field,thermal stresses and displacements of layered cylindrical shells.
Acknowledgement:This work is financially supported by the Transportation Science and Technology Project of Jiangsu Province (Grant No.2014Y01),the Seed Funding Program for Basic Research of the University of Hong Kong,the Research Foundation for Advanced Talents of Jiangsu University (Grant No.16JDG053)and the Basic Research Program of Jiangsu Province (Grant No.BK20160519,BK20160536).
Appendix A.



Appendix B.
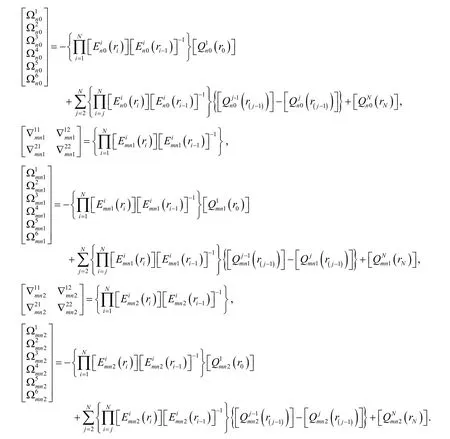
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- A Semi-Discretizing Method Based Efficient Model for Fluidelastic Instability Threshold Prediction of Tube Bundles
- Numerical Analysis of Tilted Cutting and F128 Brushes
- The Exact Inference of Beta Process and Beta Bernoulli Process From Finite Observations
- CPAC:Energy-Efficient Algorithm for IoT Sensor Networks Based on Enhanced Hybrid Intelligent Swarm
- Finite Element Investigation of Flow Field Below Asymmetric Drill Bits for Reverse Circulation in Drilling Tight Oil and Gas Reservoirs
- Novel Ensemble Modeling Method for Enhancing Subset Diversity Using Clustering Indicator Vector Based on Stacked Autoencoder
