为学生数学思维能力的提升而教
2019-11-25胡文兵
胡文兵
【关键词】经历过程;思维能力;組合图形的面积
【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009(2019)73-0053-03
组合图形是相对于正方形、长方形、三角形等基本图形来说比较复杂的平面几何图形。学习这些图形的面积计算,是基于面积概念(即“物体所占平面图形的大小”)的掌握,通过把组合图形分或补成一个或几个基本图形后进行的。因此,本课的学习对学生进一步理解什么是面积及提高面积的计算能力具有很好的巩固和促进作用。要想更好地掌握这部分内容,首先,要弄清小学数学里的组合图形的概念。小学数学里的组合图形通常是指一个或几个基本图形拼合而成的平面几何图形。它是在完成了基本图形(即长方形、正方形、平行四边形、三角形、梯形等图形)的面积教学后学习的内容。在掌握基本图形的面积计算后教学这部分内容,有两点考量:一是基于学生在生活中的认识。在生活中,学生经常会见到这类图形,有时也要解决这些图形的面积问题,这时学习有助于学生掌握解决问题的方法及技巧;二是进一步巩固基本图形的面积计算方法。要计算组合图形的面积,要么通过添补法把组合图形转化成几个基本图形,要么通过分割法把组合图形分成几个基本图形,已学过的基本图形的面积计算是求组合图形面积的知识基础,同时又能在计算组合图形面积时得到巩固。其次,要引导学生在操作实践中经历知识的抽象过程。本课的教学是从简单分类开始的。学生学会分类对于他们今后学习推理及内化数学概念具有非常重要的作用。众所周知,数学学科是一门抽象性很强的学科。数学抽象的结果来自知识抽象的过程,有效的数学学习不能只注重抽象结果,更要让学生经历抽象的过程。
一、复习旧知,引入新课
1.出示如图1所示的一组图形。
(1)小组讨论:这组图形如果让你来分一分,可以怎么分?为什么?
(2)小组汇报:
生1:我们根据图形的边数,把①③④⑤号图形分为一类,②号图形分为一类,⑥号图形分为一类。①③④⑤号图形是四条边,②号图形是五条边,⑥号图形是三条边。
师:不错!还有不同的分法吗?
生2:我们把①③④⑤⑥号图形分为一类,②号图形分为一类。第一类是很简单的图形,第二类图形稍复杂些。
师:在数学上,第一类简单的图形叫“基本图形”,第二类稍复杂的图形叫“组合图形”(板书课题)。
2.复习基本图形的面积计算公式:我们已经学习过基本图形的面积计算,是怎么算的?你能说一说吗?
3.揭示课题:组合图形的面积如何计算呢?这节课我们就来一起探讨。(板书:面积)
上述教学片段,通过让学生将一组图形进行分类,使他们直观地感知组合图形和基本图形的不同。基本图形的面积计算直接利用公式即可,组合图形的面积计算则不能,以旧知复习引入课题水到渠成。
二、探究新知,理清思路
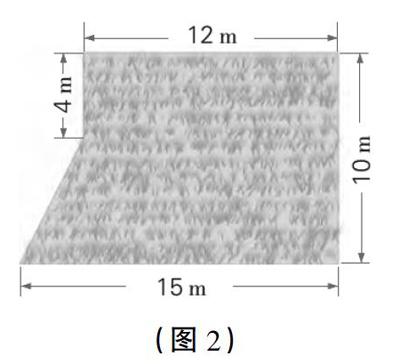
出示例10:华丰小学校园里有一块草坪(如图2),它的面积是多少平方米?
1.方法初探:你准备怎样算?讨论后汇报。
生1:可以把这个图形分成两个图形。
师:你的策略是分一分(板书:分割法),那分到的两个图形我们叫什么图形?
生1:基本图形。
师:如何求面积?
生1:把分到的两个基本图形的面积分别求出来,相加就得到组合图形的面积。
师:还有不同的想法吗?
生2:还可以把左边缺的一块补上,原来的组合图形就成了一个长方形,用长方形面积减去补的梯形面积就得到组合图形的面积。
师:这个想法很好!我们把刚刚那个方法叫分割法,那这个方法叫什么呢?
生2:添补法。(板书)
2.方法深探:根据大家的想法,这个组合图形能怎样分割,又能怎样添补呢?
(1)单独分一分或补一补。
(2)小组讨论:在小组内与同学交流。
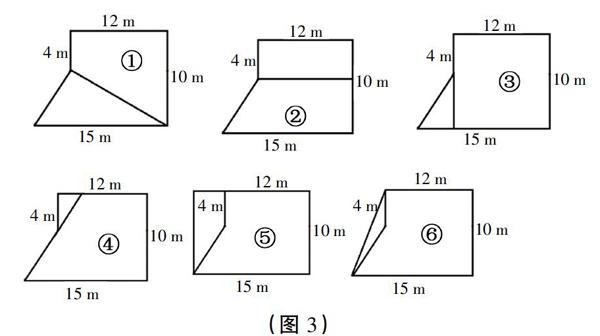
(3)交流汇报:学生通过分割或添补得到图形。(根据不同方法相机板书,形成如图3所示的6个图形)
在学生初步知道组合图形的面积不能直接计算后,教师引导他们进行两个思维层次的探究。在学生初步了解计算组合图形面积的两种方法——分割法和添补法后,让他们通过画一画、连一连体验两种方法的不同。
3.计算并交流。
(1)计算。请大家从上述6个图形中选择一种,利用给出的数据来独立计算一下它们的面积。
(2)汇报并大组交流:
①号图形:10-4=6m,15×6÷2=45m2,(4+10)×12÷2=84m2,84+45=129m2。
②号图形:10-4=6m,(12+15)×6÷2=81m2,12×4=48m2,81+48=129m2。
③号图形:15-12=3m,10-4=6m,3×6÷2=9m2,12×10=120m2,9+120=129m2。
④号图形:没人回答。
⑤号图形:15-12=3m,(4+10)×3÷2=21m2,15×10=150m2,150-21=129m2。
⑥号图形:15-12=3m,4×3÷2=6m2,(12+15)×10÷2=135m2,135-6=129m2。
师:④号图形怎么没人回答?
生:④号图形分成的是梯形和三角形,根据给出的数据不能求出它们各自的面积,也就不能算出组合图形的面积。
师:说得真好!④号图形虽然可以这样分割,但求不出它们各自的面积。可见,同学们在利用分割或添补的方法计算组合图形的面积时,要注意什么?
生1:在分割组合图形时,分到的每个图形都要能结合给出的条件分别求出它们的面积才行。
生2:添补的方法也一样,要能结合给出的条件分别求出补成图形的面积才行。
师:说得真不错!给同学们点赞!⑥号图形的方法同学们在理解上可能有点困难,因为这种情况下高的画法在小学阶段不作要求。
(3)小组讨论并汇报:计算组合图形的面积时,这两种方法有什么相同点和不同点?
生1:分割的方法最后是把分到的几个基本图形的面积相加,用的是加法。
生2:添补的方法是从补得的基本图形中把多余部分的面积减去,用的是减法。
生3:用这两种方法计算组合图形的面积时,都要先算出分割后或添补成的基本图形的面积。
师:说得真好!
学生在动手分或补之后,可行还是不可行,要通过能否分别计算出组合图形的面积来检验。在一环扣一环的提问和交流中,学生的思维不断碰撞,逐渐体悟出在利用分割法或添补法时,要以能分别求出分或补得的每个基本图形的面积为前提。最后的讨论总结带领学生厘清了组合图形面积计算的思路。
三、渗透转化,思维巩固
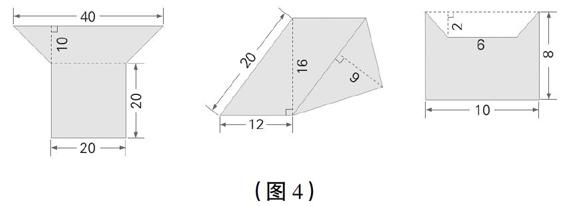
师:带着上面的收获,我们来求下图4中各个图形的面积,并在小组内交流不同的计算方法,比较一下,找出你认为最好的方法。
小结:从计算方法最优化或最简化的角度来看,有的组合图形一看就能确定选择分割法还是添补法。如一看就知道第一个图能用分割法,第三个图能用添补法。
通过练习巩固,让学生进一步明晰计算组合图形的面积时如何选择分割法和添补法,在实践中感悟两种方法的取舍。
总之,本课通过让学生经历探究知识的全过程,使他们既巩固了简单基本图形的面积计算方法,又掌握了复杂组合图形的面积计算方法,在一定程度上促进了学生思维能力的提升。
(作者单位:江苏省盐城市大丰区万盈小学)
