点乘双根法解决一类直线与圆锥曲线相交弦问题

胡贵平

(甘肃省白银市第一中学 730900)

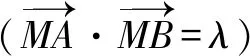
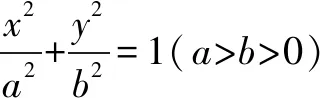
(1)求椭圆C的方程；

(2)直线不经过点A(0,1),且与椭圆交于M,N两点,若以MN为直径的圆经过点A,求证:直线l过定点,并求出该定点的坐标.

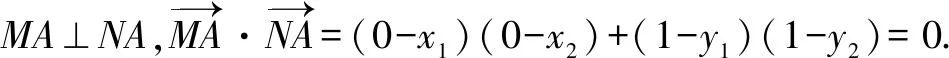
x2+2(kx+m)2-2=(1+2k2)(x1-x)(x2-x) (1)

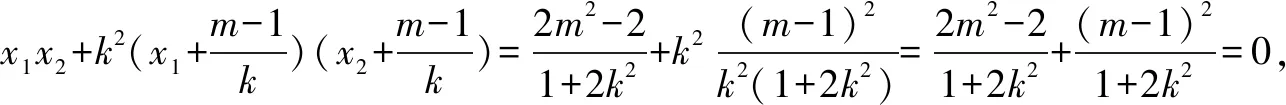
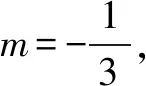
(1)求直线AB的斜率；

(2)设M为曲线C上一点，C在M处的切线与直线AB平行，且AM⊥BM，求直线AB的方程．

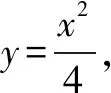
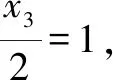
设直线AB的方程为y=x+m，因为点A,B在直线AB上,所以y1=x1+m,y2=x2+m,

所以(x1-2)(x2-2)+(x1+m-1)(x2+m-1)=0.

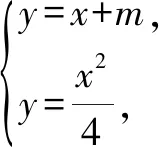
因为x1,x2是方程x2-4x-4m=0的两个根,所以x2-4x-4m=(x1-x)(x2-x) (1)

在(1)式中令x=2,得22-4×2-4m=(x1-2)(x2-2)．

在(1)式中令x=1-m,得(1-m)2-4×(1-m)-4m=(x1+m-1)(x2+m-1)，所以

(x1-2)(x2-2)+(x1+m-1)(x2+m-1)=22-4×2-4m+(1-m)2-4×(1-m)-4m=0．

解得m=-1(舍)，m=7，所以直线AB的方程为y=x+7．

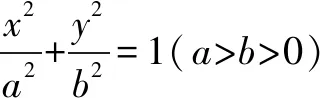
(1)求椭圆的方程；

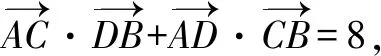
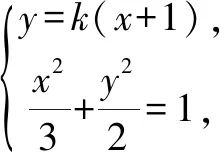
因为x1,x2是方程2x2+3k2(x+1)2-6=0的两个根,

所以2x2+3k2(x+1)2-6=(2+3k2)(x1-x)(x2-x). (1)

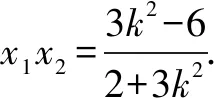
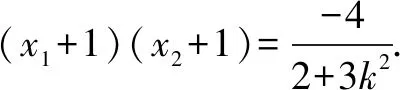
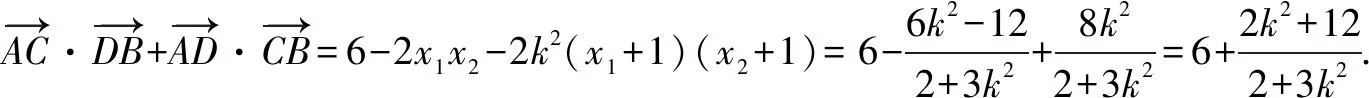
例4 (2012重庆理)设椭圆中心在原点O，长轴在x轴上，上顶点为A，左右焦点分别为F1,F2，线段OF1,OF2中点分别为B1,B2，且△AB1B2是面积为4的直角三角形.

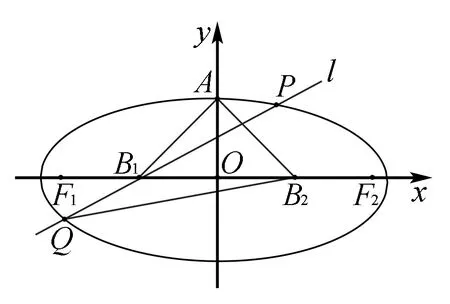
(1)求该椭圆的离心率和标准方程；

(2)过B1作直线l交椭圆于P,Q两点，使PB2⊥QB2，求直线l的方程.

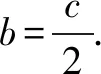
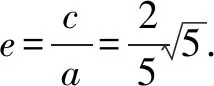
由题设条件S△AB1B2=4，得b2=4，从而a2=5b2=20.

(2)易知直线l不与轴垂直,则设直线l方程为y=k(x+2),P(x1,y1)，Q(x2,y2) .