一类题型 多向延伸

周儒省

(广东省高州中学 525200)

高中生对知识的学习以及掌握相对来说都是比较零散而片面的，尤其数学，常常对各个知识点都独立地应用，顾此而忘彼，对整个知识点没有一个总的概括，更别说知识点之间的内在联系性了，从而使得学生对知识的理解只停留在肤浅的表面，大大地阻碍了他们更深入地探究与钻研.为此我们作为老师就应该在平时的教学中有意识地培养学生的归纳整理和延伸拓展思维能力的培养.下面主要以两类关于线圆的类型题来分析如何点面扩散培养学生的归纳拓展思维，希望对大家能起到抛砖引玉的作用.

一、过交点求方程问题

例1 求过直线2x+y+4=0与圆C2:x2+y2+2x-4y+1=0的交点且有最小面积的圆的方程.

分析通俗做法就是联立直线与圆的方程构建出一个二元二次方程组，解此方程组得出两个交点的的坐标，然后设出所求圆的一般方程，结合圆心到两交点的距离等于半径和圆面积最小则半径最小，得出一个三元二次方程组，解此方程组得出所求圆的方程.

然而，此思路虽然不复杂但求解三元二次方程组却比较繁琐且容易出错.下面我们一起来探讨一种比较新颖的方法.

设一新的方程：x2+y2+2x-4y+1+λ(2x+y+4)=0 其中λ为一个可变的常数则自然会问此方程表示的是怎样的几何图形，不妨将方程转换一下

x2+y2+(2λ+2)x+(λ-4)y+4λ+1=0.

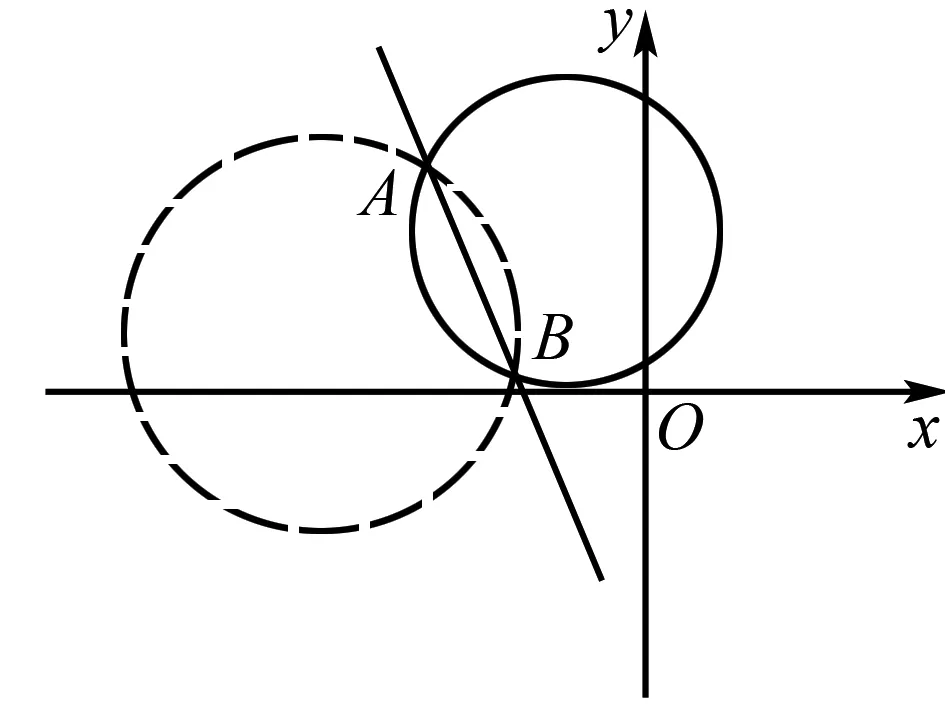
明显符合圆的一般方程，因此所设的方程x2+y2+2x-4y+1+λ(2x+y+4)=0表示的是一个圆，如图交点A、B的坐标满足方程组

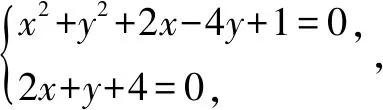
x2+y2+2x-4y+1+λ(2x+y+4)=0.

又因为λ是一个可变的常数，那么容易知道过A、B两点的所有圆都可以用下面的方程来表示

x2+y2+2x-4y+1+λ(2x+y+4)=0.

因此，题目所求的圆的方程可设为

x2+y2+2x-4y+1+λ(2x+y+4)=0,其中λ为一个可变的常数.

化为圆的标准方程：

然而教师不应就此打住，而该带有好奇心地向同学们提问：能否将此方法延伸到其他情况中去呢？给几分钟时间让学生们探索及讨论，然后各抒己见，同时将班里所有情况列出.最后老师也将自己的知识总结罗列出来：

凡是涉及到有交点求方程的(线与线、线与圆、圆与圆)，都可设所求方程为：

已知一个方程+另一个方程的λ倍=0.

(1)求直线l3过直线l1:A1x+B1y+C1=0与直线l2:A2x+B2y+C2=0交点的方程(或求直线l1关于直线l2对称的直线l3的方程)，都可设直线l3的方程为：

A1x+B1y+C1+λ(A2x+B2y+C2)=0.

(2)求过直线l:Ax+By+C=0与⊙O:x2+y2+Dx+Ey+F=0交点的⊙O2的方程，都可设⊙O2的方程为：

x2+y2+Dx+Ey+F+λ(Ax+By+C)=0.

(3)求过⊙O1:x2+y2+D1x+E1y+F1=0与⊙O2:x2+y2+D2x+E2y+F2=0交点的⊙O3的方程，都可设⊙O3的方程为：

x2+y2+D1x+E1y+F1

+λ(x2+y2+D2x+E2y+F2)=0.

更甚者，可将一点看成为半径为0的圆，如：求与直线l:Ax+By+C=0相切且切点为P(x0,y0)的⊙O的方程，此时点P(x0,y0)可看成圆心为P半径为0的圆且其方程为：(x-x0)2+(y-y0)2=0，那么可设所求圆的方程为：

(x-x0)2+(y-y0)2+λ(Ax+By+C)=0.

此方法亦可延伸至求过某特定点的圆的方程.

评析本题通过引入一个可变常数λ，设出过交点的所有圆的方程，结合题设条件求出λ值，从而得到所求圆的方程，避免了常规做法，尤其大大地简化了计算，更为重要的是整道题对同学来说有种焕然一新的感悟！而后面的引导归纳，更是由此思想延伸而拓展得到的.这样不仅能有效地提高同学们对知识的归化整理能力，在头脑中对此类型问题就有一个比较全新的方法去解题，并且于做题过程中同学们会潜移默化地逐渐形成举一反三的延伸思考，进而逐步养成对事情进行点联想到面的归纳和拓展思索，从而大大地提升了学生学习的效果.

二、求最值问题

例2 已知⊙C过⊙C1:x2+y2-4x-4=0与⊙C2:x2+y2-4y-6=0的交点，且⊙C关于直线l:y=x对称.

(1)求⊙C的方程；

(2)若x,y满足⊙C的方程，试求

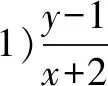
2)y-x的最值.

分析此题第(2)问乍一看无法下手，然而细想此例与我们学习过的斜率计算公式可对入号，而相减却与求直线在坐标轴上的截距相关.详细解题过程如下：

解(1)∵⊙C过⊙C1:x2+y2-4x-4=0与⊙C2:x2+y2-4y-6=0的交点,

∴⊙C的方程可设为：

x2+y2-4x-4+λ(x2+y2-4y-6)=0,

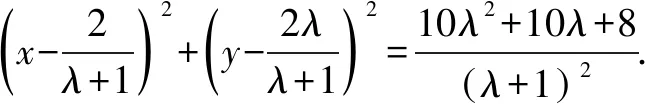
又∵⊙C关于直线l:y=x对称

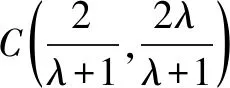
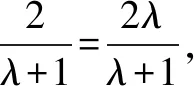
∴⊙C的方程方程为：(x-1)2+(y-1)2=7.

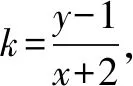
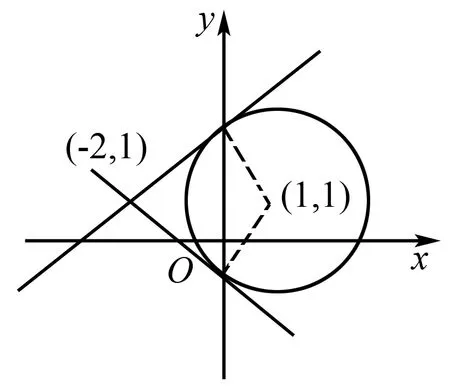
∴k表示是过定点(-2,1)和动点(x,y)的直线l的斜率.

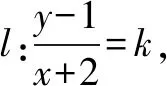
kx-y+2k+1=0.

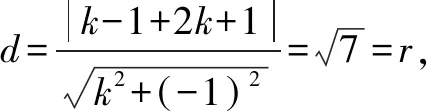
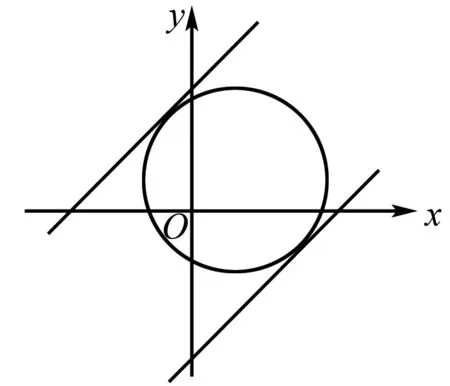
②设y-x=b(y=x+b)，则题目所求的最值问题就是求b的最值问题，也就是直线与圆有公共点的条件下求直线y=x+b在y轴上截距b的最值.由图可知：当直线y=x+b与⊙C相切时才取得最值，此时，圆心C到直线l的距离等于半径r，即：

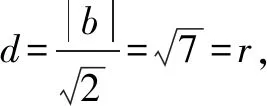
∴(y-x)min=-14，(y-x)max=14.

同时教师不应该就此结束，而逐渐引导学生对于一些求最值问题的一些知识点的总结和归纳：

(1)求形如：(x-a)2+(y-b)2的最小值，可转化为求定点P(a,b)到动点M(x,y)的线段|PM|的最小值，结合点到直线的距离最短和距离公式可求得.

注意：x2+y2事实上是定点(0,0)到动点M(x,y)的距离的平方.

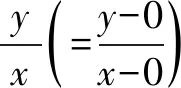
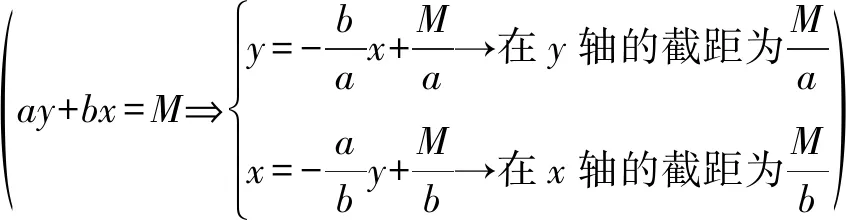
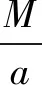
注意：求y±x的最值，事实上就是求直线y±x=b(y=∓x+b)在y轴上的截距b的最值.

评析此题主要利用学过的斜率与截距的相关知识来解题，同时结合数形结合的思想，大大地培养了我们将抽象转化为具体，激化对学习的求知欲！同时也因此而引出对其他求最值问题的一些方法总结，从而使学生渐渐地形成对知识间联系的思考和探讨，逐渐形成一个由点到面的大格局知识框架，大大增强同学们的归纳整理思维，形成对事物的繁衍性思考，从而大大地提升他们学习的效率！

总之，于平常的课题教学中我们教师应当有意识地进行对各个模块知识的串联及延伸，由点及面、举一反三、思此顾彼，灵活掌握，进而激发学生发散思维学习，对所接触所学习的事和物于老师的系统讲学、分析演绎中潜移默化地养成归纳总结和拓展延伸思维，久而久之，学生的学习效率也会逐渐的提升.于另一个层面上，也为同学们日后进入高校深造系统学习高等知识打下牢固思维格局，初步形成框架分块且串联延伸的合理思考，更便于他们日后的学习.