EP 元的一些新刻画

史丽妍,马丽,魏俊潮

(扬州大学数学科学学院,江苏扬州225002)

1 引言

本文所涉及的环均表示有单位元的结合环.设R是一个环,a∈R, 若存在c∈R, 使得

则称a为R的群可逆元[1], 且称c为a的群逆元.由文献[2]知, 群可逆元a的群逆元是唯一确定的, 通常记为a#.本文用R#表示环R的全体群可逆元的集合.

设R为一个环,∗为环R到R的一个双射, 满足条件(a∗)∗=a; (a+b)∗=a∗+b∗;(ab)∗=b∗a∗, 其中a,b∈R, 则称R为一个对合环, 有时也简称R为∗-环[3].

设a∈R, 若存在x∈R, 满足a=axa;x=xax; (ax)∗=ax; (xa)∗=xa, 则称a为Moore Penrose 可逆元, 简称a为MP 可逆元,x称为a的MP 逆元.由文献[4]知, MP 可逆元a的MP 逆元是唯一确定的, 记为a†.用R†表示∗-环R的全体MP 可逆元的集合.

设R为∗-环, 若a∈R#∩R†且a†=a#, 则称a为R的EP 元[5].用REP表示R的全体EP 元的集合.EP 元的研究起源于矩阵广义逆与算子广义逆, 最早可追溯到对EP 矩阵[6]的研究.对EP 矩阵的刻画还可参见文献[7 −11].本文主要从纯环论的角度研究EP 元,通过构造几个特定的方程, 研究其解与结合∗-环上一个core 可逆元成为EP 元的等价条件,这是环论上研究EP 元的一种新型的方法.

2 主要结果

引理1[12]设a∈R#∩R†, 则

(1)Ra=Ra2=Ra#=Ra†a=Ra∗a=Ra#a;

(2)aR=a2R=a#R=aa†R=aa∗R;

(3)Ra∗=Ra†=R(a∗)2=Raa∗;

(4)a∗R=a†R=(a∗)2R=a∗aR.

若a∈R#∩R†且aa#=(aa#)∗, 则a∈REP.因此当aa#=aa†时必有a∈REP.从而有下面的引理.

引理2[13]设a∈R#∩R†,

(1) 若Ra⊆Ra∗, 则a∈REP;

(2) 若Ra∗⊆Ra, 则a∈REP;

(3) 若aR⊆a∗R, 则a∈REP;

(4) 若a∗R⊆aR, 则a∈REP.

设R为∗-环,a∈R#∩R†, 则(a#)∗=(a∗)#, (a†)∗=(a∗)†, (a†)†=a.由于(a#)†及(a†)#未必存在, 因此记χa={a,a∗,a†,a#,(a#)∗,(a†)∗}.

定理3设a∈R#∩R†, 则a∈REP当且仅当下面的方程(2.1) 在χa中至少有一个解,

证必要性由于a∈REP, 所以a†=a#.易见a†aa∗a=a∗a,a∗a2a†=a∗a2a#=a∗a,从而x=a†为方程(2.1) 在χa中的一个解.

充分性(1) 若x=a为解, 则a2a∗a=a∗a3.从而由引理1 知aR=a2R=a(aa∗R)=a2a∗R=a2(a∗aR)=a2a∗aR=a∗a3R=a∗aR=a∗R, 由引理2 知a∈REP.

(2) 若x=a#为解, 则a#aa∗a=a∗a2a#=a∗a.由引理1 知

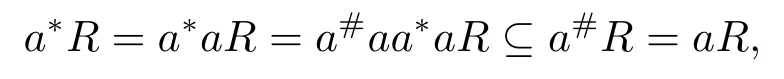
由引理2 知a∈REP.

(3) 若x=a†为解, 则a†aa∗a=a∗a2a†, 即a∗a=a∗a2a†.由引理1 知

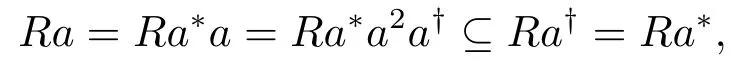
由引理2 知a∈REP.

(4) 若x=a∗为解, 则

将(2.2)左乘(a†)∗得aa∗a=a2a∗, 由引理1 得

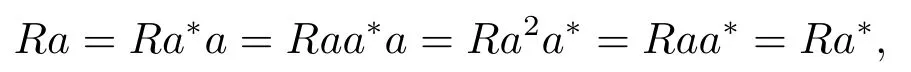
由引理2 知a∈REP.

(5) 若x=(a#)∗为解, 则

对(2.3)应用对合得a∗aa∗a#=a#a∗a∗a, 由引理1 知

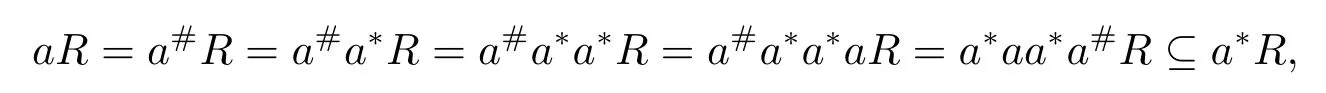
由引理2 知a∈REP.

(6) 若x=(a†)∗为解, 则

对(2.4)应用对合得a∗aa∗a†=a†a∗a∗a, 由引理1 知

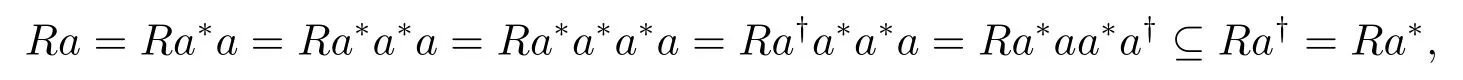
由引理2 知a∈REP.

注意到x∈χa当且仅当x∗∈χa, 因此对方程(2.1)两边取对合可得下面的方程

由定理3 可得如下推论.

推论4设a∈R#∩R†, 则a∈REP当且仅当上面的方程(2.5)在χa中至少有一个解.

由于a∈REP当且仅当a∗∈REP, 因此把方程(2.1)中的a换成a∗, 可得下面的方程

利用定理3，可得如下推论.

推论5设a∈R#∩R†, 则a∈REP当且仅当上面的方程(2.6)在χa中至少有一个解.

把方程(2.6)两边取对合可得下面的方程

由推论5 知有下面的推论.

推论6设a∈R#∩R†, 则a∈REP当且仅当上面的方程(2.7)在χa中至少有一个解.

定理7设a∈R#∩R†, 若下列条件之一成立, 则a∈REP.

(1)a2a∗=a∗a3a†;

(2)a#aa∗=a∗;

(3) (a†)∗aa∗=a∗a2(a†)∗a†.

证(1) 由于a2a∗=a∗a3a†, 右乘a得a2a∗a=a∗a3.由定理3 充分性的证明(1) 知a∈REP.

(2) 由于a#aa∗=a∗, 右乘(a†)∗得a#a=a†a, 故a∈REP.

(3) 由于(a†)∗=(a†aa†)∗=(a†)∗a†a, 从而R(a†)∗⊆Ra.又a=aa†a=a(a†a)∗=aa∗(a†)∗, 从而Ra⊆R(a†)∗, 于是R(a†)∗=Ra.由于(a†)∗aa∗=a∗a2(a†)∗a†, 两边取对合得

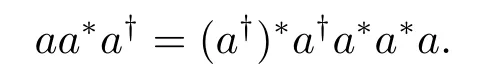
故由引理1 知Ra=Ra∗a=Ra∗a∗a=Ra∗a∗a∗a=Ra†a∗a∗a=Raa†a∗a∗a=R(a†)∗a†a∗a∗a=Raa∗a†⊆Ra†=Ra∗, 由引理2 知a∈REP.

推论8设a∈R#∩R†, 则Ra=R(a†)∗;aR=(a†)∗R.

方程(2.1)右乘a†得下面的方程

由定理7 知当x=a,a#, (a†)∗为方程(2.8)的解时, 都有a∈REP.