血型判读系统中的边缘检测算法研究

姚娜 ，杨波 ，李桐 ，郭滨 ，马海涛

（1.长春理工大学 电子信息工程学院，长春 130022；2.吉林大学 通信工程学院，长春 130012；3.长春国科医工科技发展有限公司，长春 130102）

在当今时代，健康已经是人们最为关注的话题之一，而血型检测作为最基本的医疗辅助工作，也获得越来越多的关注。但是在发展中国家的农村地区，那里根本没有实验室和训练有素的技术人员。虽然有来自密克罗尼西亚、埃尔登生物制剂等公司的应用护理点的解决方案，但对于发展中国家的大规模使用来说，这些方案的价格高得让人望而却步（每次测试10～20美元不等）［1］。所以，便携式血型检测装置的出现是必然的，但是便携式的血液检测装置也会面对很多技术问题，其中在没有专业的医疗条件情况下获取到的数字图像背景光不均匀就是其中一个，如若不能很好的解决背景光的问题，那么就会影响边缘检测进而影响血型判读结果。

针对图像背景不均匀的问题，很多学者提出了解决办法，其中同态滤波是常用的方法之一。但是同态滤波增强是从整体的角度对图像进行光照不均修正，虽然可以在不丢失信息的情况下去除背景影响，却没有充分考虑图像的空间局部特性，这样就会出现在增强一部分时，其余部分出现过增强的现象。2013年，张亚飞、谢明鸿［2］提出局部同态滤波算法，即对图像的各个子图像分别进行同态滤波，然后对局部同态滤波产生的块效应采用相邻子图像边界平均的方法进行去除。但是，实现复杂且块效应去除不明显，很容易产生新的边缘。2018年，李开伟、张立亭等人［3］基于同态滤波原理，设计新的滤波函数从而达到细节增强，影像清晰的目的。但是其对新滤波函数的构造较复杂，且之后对高频和低频分量的处理效果不够明显。当然也有从边缘检测算法方面做优化的，例如2015年，秦雪、王欢等人［4］提出基于图像边缘检测的图像识别算法用来改善得到的边缘信息，但是在光源影响较大时还是会出现检测结果亮度不均匀的现象。针对以上问题，本文提出在进行同态滤波后使用数学形态学中的高低帽变换来减少部分像素过增强的影响。

1 原理和方法

1.1 同态滤波

同态滤波（Homomorphic filter）是信号与图像处理中的一种常用技术，它采用了一种线性滤波在不同域中的非线性映射，也是一种在频域中进行的图像对比度增强和压缩图像亮度范围的特殊方法。同态滤波器不但能够减少低频并且增加高频，还能减少光照变化并锐化边缘细节。图像的同态滤波技术的依据是图像获取过程中的照明反射成像原理，如图1所示。

图1 图像获取原理图

其中，L(x,y)表示入射光源产生的亮度图像；R(x,y)代表物体本身产生的反射图像；S(x,y)是观察到的图像。根据兰德提出的理论，对于给定图像S(x,y)中的每个点都可以用公式表示为：

一般来说，亮度图像L(x,y)变化缓慢，主要是低频成分，反射图像R(x,y)反应物体细节，体现为高频成分。当想要去除背景光不均匀时也就是在给定图像S(x,y)中分离亮度图像L(x,y)和反射图像R(x,y)，并分别采取压缩低频、提升高频的方法，就可以达到减弱照度分量、增强反射分量从而使图像清晰的目的。由于亮度图像相当于乘性噪声，直接运算不方便，所以先对待增强图像取对数，然后进行傅立叶变换，在频域中利用同态滤波器H(u,v)进行滤波，最后通过逆傅立叶变换及指数变换得到增强后的图像，过程如图2所示。其中G(x,y)是同态滤波后图像。在同态滤波中，滤波效果的好坏取决于滤波函数H(u,v)，为了压制低频的亮度分量，增强高频的反射分量，滤波器H(u,v)应是一个高通滤波器，但又不能完全清除低频分量，仅作适当压制。因此，同态滤波器一般采用如下形式，即：

式中，γL＜1和γH＞1控制滤波器幅度的范围；Hhp(u,v)通常为高通滤波器，如高斯高通滤波器、巴特沃兹高通滤波器、Laplacian滤波器等。由于高斯函数的傅立叶变换仍是高斯函数，所以此次同态滤波使用高斯高通滤波器。

图2 同态滤波过程

由于同态滤波是全局性滤波，所以就会在对一部分进行滤波增强时，另一部分过增强。为避免出现上述现象，本文提出使用数学形态学中的高低帽变换来去除过增强的影响。

1.2 数学形态学

1.2.1 图像膨胀、腐蚀

膨胀和腐蚀这两种操作是形态学处理的基础，许多形态学算法都是以这两种运算为基础的［5］。在灰度形态学方法中，膨胀是一种对图像的扩张变换。通过膨胀变换，对图像的外部进行滤波处理，可以填充图像中的小孔及在图像边缘处的小凹陷部分，并使整幅图像的灰度值提高［6］。腐蚀算法是一种收缩变换，对图像内部做滤波处理，可以消除小且无意义的物体，通过腐蚀变换能降低整幅图像的灰度值［7］。

设f(s,t)是输入图像，b(x,y)是结构元素，其中Df和Db分别是f和b的定义域，用b对f进行灰度膨胀，表示为f⊕b，膨胀后的灰度图像像素为：

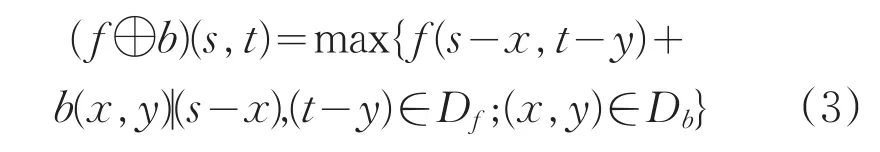
式中，(s-x)和(t-y)必须在f的定义域内以及x和y必须在b的定义域内。

用b对f进行灰度腐蚀，表示为f-b，并定义腐蚀后的灰度图像素值为：

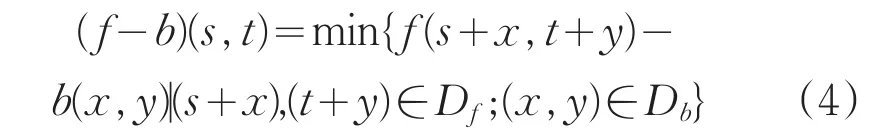
式中，(s+x)和(t+y)必须在f的定义域内以及x和y必须在b的定义域内。

1.2.2 高、低帽变换

对图像先进行腐蚀操作，再进行膨胀操作，即图像的开运算。结构元素b对f的开运算记为f∘b，定义为f∘b=(f-b)⊕b。开运算能够除去孤立的小点、毛刺和小桥，而总的位置和形状不变。并且开运算是一个基于几何运算的滤波器，结构元素大小的不同将导致滤波效果的不同，而不同的结构元素也会导致不同的分割，即提取出不同的特征［8］。

对图像先进行膨胀操作，再进行腐蚀操作，即图像的闭运算。结构元素b对f的闭运算记为f·b，定义为f⋅b=(f⊕b)-b。闭运算能够填平小孔，弥合小裂缝，而总的位置和形状不变。并且闭运算是通过填充图像的凹角来滤波图像的，结构元素大小的不同将导致滤波效果的不同，而不同结构元素同样会导致不同的分割。

从原图像中减去开运算的图像称为顶帽变换，也称为高帽变换。设g(x,y)为输出图像，顶帽变换即为g=f-(f∘b)，高帽变换可以求出图像中的峰值。用闭运算的图像减去原图像称为底帽变换，也称为低帽变换。若h(x,y)为输出图像，顶帽变换即为h=(f⋅b)-f，而低帽变换可以求出图像中的谷值。这两个变换都是用一个结构元素通过开操作或闭操作从一副图像中删除物体，而不是拟合被删除的物体［9］。然后，差操作得到一副仅保留已删除分量的图像。所以经过高低帽变换可以对原图像进行增强，使边界更加鲜明。高帽变换用于暗背景上的亮物体，而低帽变换则用于亮背景上的暗物体［10］。由于这一原因，当谈到这两个变换时，常常分别称为白顶帽变换和黑底帽变换。由于本实验获得的原灰度图像是亮背景、暗物体，而低帽变换的结果是暗背景、亮物体，高帽变换得到的结果是暗物体、亮背景。所以，为得到和原灰度图像相同的处理效果，本实验采用在原图的基础上叠加顶帽变换后减去低帽变换后的图像（若z(x,y)为输出图像，即z=(f+h)-g）的办法来去除过增强的影响。

2 仿真实验及结果

由于本次的实验目的是得到血型判读结果，所以得到正确的边缘信息是必要的。本实验使用微流卡作为血液样本载体，其检测血型原理和其他试管或者试纸检测原理相同。其中数字图像结果是通过普通的智能手机拍照获得的，如图3所示。其血型结果判读过程如图4所示。

图3 原图

图4 图像处理过程流程图

根据上述处理过程得到待检测血液样本有哪几种（抗A、抗B和抗D）发生凝集反应，在图像上表现为边缘是否连续，进而判断出对应的血型。由于Canny算子属于先平滑后求导数的方法，且根据对信噪比与定位乘积进行测度，相对其他检测方法可以得到最优化逼近算子，所以本次边缘检测使用Canny算子。为验证高低帽变换确实去除了过增强的影响，本次实验在MATLAB仿真实验平台上进行。实验过程：首先对获得的数字图像灰度化，然后在相同的条件下进行同态滤波和同态滤波后进行数学形态学高低帽变换的图像进行对比，进而得出结论。

2.1 同态滤波

首先对得到的数字图像进行灰度化，结果如图5所示。从图6原图的二值化图像中可见，如果此时对其进行边缘检测是得不到完整的边缘信息的，所以此时采用同态滤波的方法进行背景消除，图7是同态滤波后的灰度图像，图8是同态滤波后的二值图像。此时，同态滤波后二值化的阈值为187，此时无论增加或减小阈值的值都不会得到更好的二值化效果，即阈值可选范围较小，不利于得到准确的二值图像，也就是说同态滤波后很难得到较好的二值化图像。其次，从边缘检测的结果（图9）中可以看出，同态滤波确实使右下角光线较暗的部分得到了改善，也能检测出边缘，即右下角亮度相对较暗的部分确实可以检测出来，但是却出现了其他部分的过增强现象，丢失部分信息。并且，对能够去除背景影响的部分的边缘也没能得到正确的边缘检测效果，这个时候是没有办法区分是否有凝集反应的，进而无法进行血型判读。在此基础上本文提出使用高低帽变换的方法来改善过增强的影响。

图5 原图的灰度图

图6 原图的二值化图像

图7 同态滤波后的灰度图像

图8 同态滤波后的二值图像

图9 同态滤波后的边缘检测图像

2.2 同态滤波后进行高低帽变换

针对同态滤波后出现的过增强现象，提出使用数学形态学中的高低帽变换进行改善。图10是使用本文方法后的灰度图像，图11和图12分别是对应的二值图像和边缘检测图像。对比图10和图7，从图像增强的角度可以看到高低帽变换使同态滤波后的灰度对比度增强，使得边缘信息更加明显，也使得二值化时可选的阈值范围增大，进而可以得到较完整的二值化图像，如图11所示。同时从图12中可以看出图像经过高低帽变换后确实可以保证在去除背景影响的同时也使得过增强的部分得到改善，即可以得到较完整且相对准确的边缘检测效果。因为只有保证检测边缘的完整性，才能正确识别是否有凝集反应为得到准确的判读结果提供技术支持。

图10 本文算法后的灰度图像

图11 本文算法后的二值图像

图12 本文算法后的边缘检测图像

2.3 有无高低帽变换数据对比

本文采用灰度直方图和三维立体图两种方式进行数据对比。

灰度直方图是灰度值的统计图形，以图形的方式反映图像灰度分布情况，灰度直方图分为两个类型。一是标准灰度直方图，表示像素个数和灰度值大小的关系；二是归一化的直方图，表示同一灰度值大小的像素所占百分比和灰度值的关系。由于本文不讨论占比，所以使用标准直方图做对比说明，图13是同态滤波后的灰度直方图，图14是本文算法后的灰度直方图，比较二者可以看出，经过高低帽变换后使得150以下的灰度像素点增多，200到255之间像素点相对减少，也就是说高低帽变换使过增强的部分得到了改善。相对于只用同态滤波进行背景影响消除，本文方法解决了同态滤波过增强的问题，得到了更好的图像边缘，为之后的血型判读工作中图像识别等工作提供技术基础。

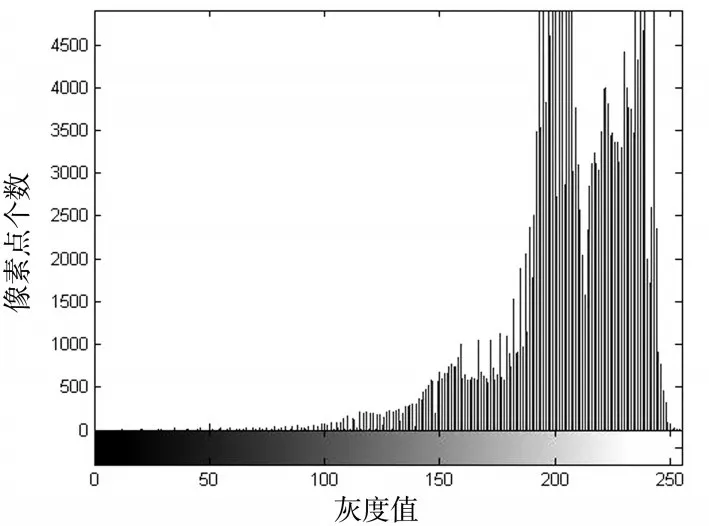
图13 同态滤波后的灰度直方图

图14 本文算法后的灰度直方图

图15 同态滤波后的三维立体图

图16 本文算法后的三维立体图

由于直方图只是显示灰度值的总数，不够具体。所以本文又使用三维立体图来进行对比说明，它既显示了整幅图片的灰度值，又显示了详细的位置信息。图15和图16分别是同态滤波后和本文算法后的三维立体图。首先，从图中可以更明显的看出经高低帽变换后图像对比度明显增强，即拉伸了灰度图像使灰度值使150以下的像素点增多。其次，从提供的位置信息上可以看出，不仅同态滤波后过增强的部分的灰度值对比明显变大，整幅图像的背景亮度也都基于一个平面，也就是说去处理背景影响的同时很好的降低了过增强的影响，也就使得有用信息和背景充分区别开来，为二值化图像提供较大阈值空间，进而得到更准确的边缘信息。另外，从提高血型判读准确率的角度来讲，经高低帽变换后图像较只通过同态滤波的图像更能提供精准的边缘信息，也就是说提高了图像识别的准确率。

综上所述，由于对图像的处理部分在血型判读系统中起着对判读结果的关键作用，所以对图像边缘的准确获取是必不可少的一个环节。经实验表明，对同态滤波后的图像进行高低帽变换可以在去除背景影响的同时防止出现过增强现象，进而得到完整且准确的边缘检测效果，为后期图像识别的工作提供准确的数据，提高血型判读的准确率。

3 结论

随着人们健康意识的逐渐增强，血型检测的重要性也越来越被大家关注，所以基于图像处理的便携式血型检测方法也被大家逐渐地接受，可是便携式血型检测器件在获取数字图像的时候，光源等干扰因素会使得背景亮度不均匀进而得不到理想的边缘检测效果，从而影响检测结果。去除背景影响常用的方法之一就是同态滤波，但是由于同态滤波是全局性滤波方法，就会使一部分图像得到滤波，另一部分出现过增强的现象。所以本文针对在同态滤波时出现的过增强现象提出使用数学形态学中的高低帽变换的方法来改善。经实验表明：在相同滤波条件下提出的办法能获得较好的二值图像和边缘检测图像，即能在很大程度上去除背景影响的同时改善过增强的影响，达到实验目的，为之后的血型判读中的图像识别等其他过程提供技术基础。