基于迭代分割的无线传感器网络定位算法

张婧，国晶

（长春理工大学 计算机科学技术学院，长春 130022）

随着物联网技术的不断发展，无线传感器网络（WSNs，wireless sensor networks）凭借着其低成本、微型化、低功耗和灵活的组网方式、铺设方式以及适合移动目标等特点称为物联网的底层支撑技术［1］。它正被广泛的应用在国防、医疗、环境、目标跟踪等多个领域。明确传感器节点的具体位置，是大多数应用服务中不可或缺的一部分。例如：在国防中只有知道突发事件（如枪声、爆炸等）的具体位置，军队才能够对事发地及时采取应对措施；对于环境监测中只有知道火灾的准确方位才能指导消防人员进行扑火操作；对于入侵监控，只有知道入侵者的行动轨迹才能进行追踪［2］。因此，无线传感器网络定位技术是大多数应用的基础，如果只知道发生的事件，却不知道具体的位置，感知的数据可能失去意义。同时，明确传感器节点所在的位置，可以提高网络的路由效率，实现网络的负载均衡和网络拓扑的自配置，使整个网络的覆盖质量得到提升［3］。因此，无线传感器网络定位是一项必不可少的关键技术。

目前，利用全球定位系统（GPS）来获取节点的位置信息是比较简单且常用的方法。然而，由于昂贵的硬件和能源问题，在每个节点上部署GPS显然不符合WSN中普通节点成本低、体积小的要求。因此，通常利用少量已知位置信息的节点（信标节点），并通过一些定位算法来实现对未知节点的定位［2］。无线传感器网络的定位算法可根据是否需要测量节点间的欧氏距离或角度分为基于测距的定位算法与非测距的定位算法。其中基于测距的定位算法有TOA（基于时间的定位方法）［4］、TDOA（基于信号传输时间差的定位方法）［5］、AOA（基于信号角度的定位方法）［6］以及RSSI（基于信号强度的定位方法）［7-8］等。非测距定位算法主要有质心算法［9］、APIT算法［10］、DV-Hop算法［11-12］等。由于非测距的定位算法无需增加额外的硬件成本，算法简单易实现，在能耗方面相比测距的定位算法有一定的优势，因而针对非测距算法中的APIT进行改进将有一定意义。

国内外学者针对APIT定位算法中存在的定位精度低的问题，提出了不少改进的方法。当未知节点邻近信标节点分布不均匀或者未知节点靠近由信标节点组成三角形的某一条边时，APIT算法可能会产生节点误判（内部节点误判成外部节点或外部节点误判成内部节点）。针对节点误判产生的误差，文献［13］利用三角形面积或角度和的方法对节点产生的误判进行修正。但由于RSSI测距具有不准确性，无法得到精确的面积或角度之和，因而使得未知节点无法准确定位。文献［14］通过部署虚拟信标节点虽然能够有效判断未知节点在三角形的内部还是外部，但部署虚拟信标节点会消耗较多的计算资源以及时间。文献［15］提出了一种协同系数APIT定位算法，利用RSSI测距和加权三角坐标的计算方法来对未知节点进行定位。虽然达到了减少定位误差和扩展定位覆盖率的效果，但该方法大大增加了硬件成本以及能耗。因此，综合各个改进算法的优势与弊端，将改进的APIT算法以及质心算法相融合，能够有效地提高APIT算法的定位覆盖率以及定位精度。

1 APIT定位算法

1.1 APIT算法定位原理

APIT是一种实现成本较低、操作简单、易于实现并且定位精度较高的算法。它的基本原理是未知节点首先收集邻近信标节点的信息，然后从这些信标节点中任意选取三个节点组成三角形。假设集合中有n个信标节点，则共有种不同的选取方法。通过这些不同的选取方法逐一判断未知节点是否位于每个三角形的内部。最后，通过计算包含目标节点所在的三角形的重叠区域的质心，并将质心作为未知节点所在的位置。如图1所示，P点为重叠区域的质心，即未知节点所在的位置［10，13］。

图1 APIT定位原理

由于在无线传感器网络中大多数节点都是静止的，所以APIT利用网络中相对较高的节点密度来模拟节点移动，利用无线信号的传播强弱来描述是否远离或靠近信标节点。其判定原理如图2所示，如果节点P运动至1的位置，将同时远离信标节点A、B、C，则P点在DABC外。另外，如果节点P运动至节点1的位置，将靠近A远离B、C，并依次对2、3、4进行相同的判断，则可判定未知节点P在DABC内。

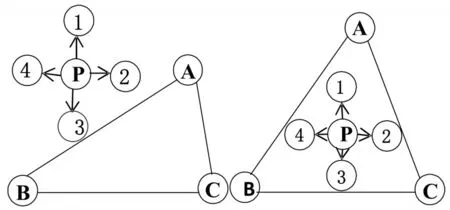
图2 PIT原理

1.2 APIT算法存在的误差

（1）In-To-Out和Out-To-In错误

在APIT定位算法中，当节点的密度较低时，可能会产生内部节点错判成外部节点（In-To-Out）和外部节点错判成内部节点（Out-To-In）的错误。如图3（a）所示，当未知节点P模拟运动2或3的位置时，未知节点P没有同时靠近或远离三个信标节点A、B、C，则可能发生Out-To-In错误［15］。同理，图3（b）未知节点P模拟运动到4的位置时，同时远离三个信标节点，则被判定未知节点在三角形外，可能产生 In-To-Out错误［15］。

（2）重叠区域过大引起的误差

当节点分布不均匀或部分未知节点邻近的信标节点数量较少时，可能会导致包含目标节点所在的三角形的重叠区域过大，进而将其重叠区域的质心作为未知节点的坐标会造成较大的误差。

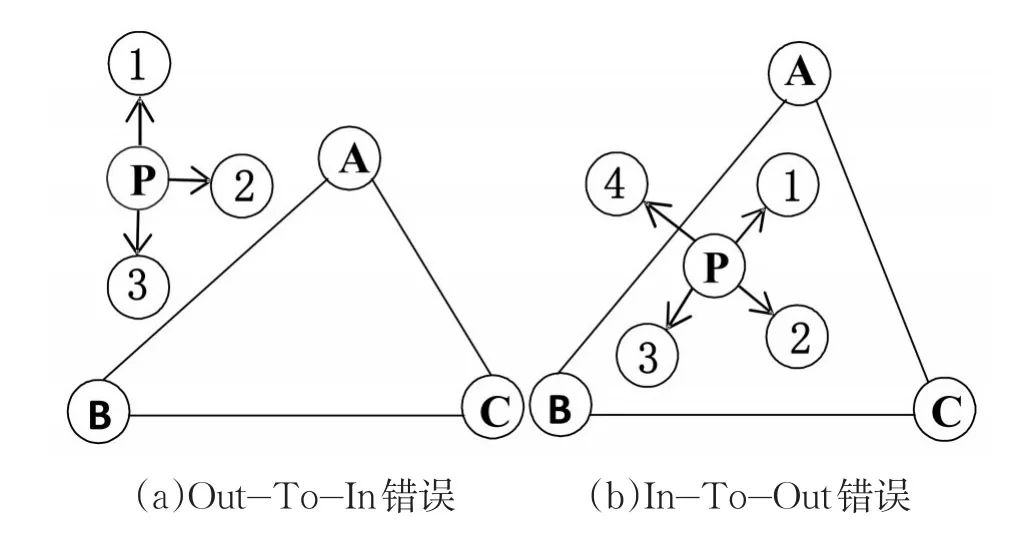
图3 误差分析

2 改进的APIT算法

2.1 三角形内点的判定

为了尽量减少APIT算法中的In-To-Out和Out-To-In引起的误差以及尽可能的提高定位精度。判定内点的方法如下：

根据同向法对节点进行判定。同向法的基本原理为：假设存在一个点P以及DABC。判断P点是否在DABC内。则需判断：

（1）P点和A点在BC这条直线的同一侧；

（2）P点和B点在AC这条直线的同一侧；

（3）P点和C点在AB这条直线的同一侧。

同时满足上述三种条件，则证明P点在DABC内，否则，P点在DABC外。

如图4所示，判断P点和A点在BC这条直线的同一侧，则过A点作BC的垂线交于F点，即∠AFB=∠AFC=90°。

若P点和A点在同一侧，

则∠AFP＜∠AFB，∠AFP＜∠AFC

故∠AFP＜90°

否则，∠AFP＞90°

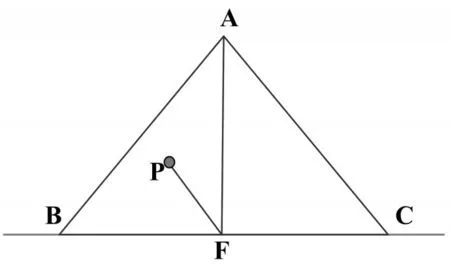
图4 同侧判定方法

通过上述证明，同理如图5所示，可得到如下命题：

命题1：若未知节点P在由三个信标节点组成的DABC内，则∠AFP，∠BHP，∠CMP的角度均小于90°。

命题2：若未知节点P在由三个信标节点组成的DABC外，则∠AFP，∠BHP，∠CMP中必然存在一个角大于90°。

其中F、H、M分别为A点、B点、C点到对边的垂足。

图5 角度判定

相应角度的计算方式如下：

（1）通过RSSI测距的数学模型公式［9］：

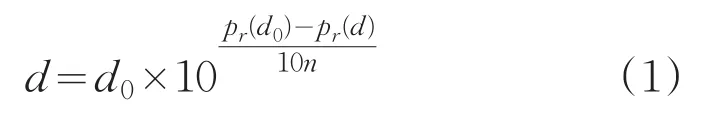
式中，d0为参考距离；Pr(d0)表示无线信号对应的接收功率；Pr(d)为接收机接收到的无线射频信号功率；n为传播因子；d表示信号的发射机器与接收机器之间的距离，即未知节点与信标节点之间的距离。

（2）如图6所示，通过两点间的距离公式求出三个信标节点A（x1，y1），B（x2，y2），C（x3，y3）之间的距离为：

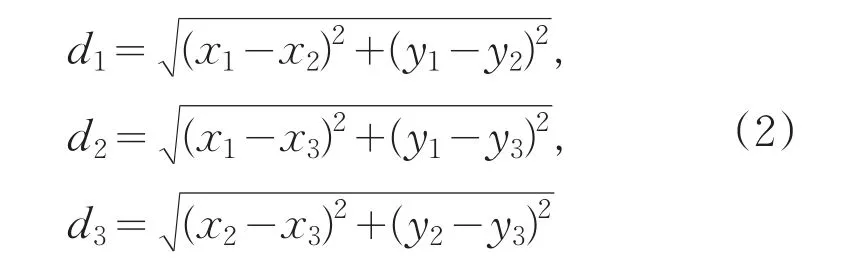
（3）由点到直线的距离公式求出AF的距离：

其中已知A、C的坐标，则a=y3-y2，b=x2-x3，c=x3×y2-x2×y3。

由余弦定理可得：

（4）求出判定角度：

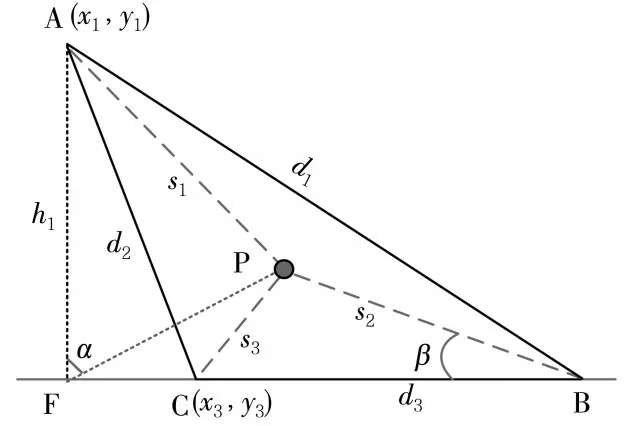
图6 角度计算

如果存在某一个三角形包含未知节点，则该三角形被定义为有效三角形。为了得到更精确的定位结果，即对有效三角形可进行区域的划分与迭代，最终求出未知节点的坐标。

2.2 有效三角形的划分与迭代

为了进一步提高未知节点的定位精度，在判定未知节点在三个信标节点所组成的三角形内之后，可以通过作垂线的方法来缩小未知节点所在区域。如图7所示，A，B，C为信标节点。在DABC内，角度由小到大的排列顺序为∠A，∠B，∠C，过C点作AB的垂线交于F点，即可求出最小角度A、垂足F以及未知节点P组成的角度∠AFP的大小。若∠AFP＞90°，则未知节点P在DBCF内，否则，未知节点P在DACF内。

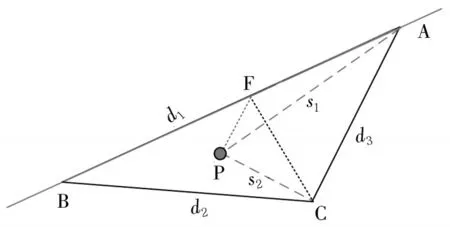
图7 区域划分

通过上述方法进行迭代分割，可得到如图8所示的迭代示意图。P点为未知节点，三个信标节点组成的三角形为DABC，最大角度为∠C，最小角度为∠A。迭代过程如下：

（1）过A点作BC的垂线交于F点，求出F点的坐标以及通过RSSI测距得到AP、BP、CP的距离；

（2）利用余弦定理可求出∠AFP角度。

（3）若 ∠AFP＞90°，则P点在DABF区域。否则，P点在DACF区域并保留P点所在的区域。假设P点在DABF区域，即令DABF中的最大角度为∠A，最小角度为∠C。

（4）重复以上步骤，直到P点所在的三角形区域为网格所能查找到的最小定位的区域（利用网格扫描法［16］所能探测到的最小单元格区域）为止。

（5）迭代结束。

图8 迭代示例图

综上，改进APIT算法的流程图如图9所示。

图9 APIT算法流程图

3 算法仿真

为了验证算法的有效性，通过MATLAB分别利用原始APIT算法、文献［13］提出基于角度和改进的APIT算法以及基于迭代分割的无线传感器网络定位算法进行仿真实验，并结合实验数据对三个算法进行性能分析与比较。实验场景设定在1 000 m×1 000 m的二维平面内，节点随机分布在监测区域内。

在仿真实验中，RSSI的各个参数值如表1所示。

表1 实验参数

场景1：设定通信半径R=100，节点总数N=300。平均运行50次，可得到如表2所示数据。

通过对实验数据表2的分析，可得出当节点总数不变时，待定位节点的平均定位误差和信标节点比例之间的关系，如图10所示。

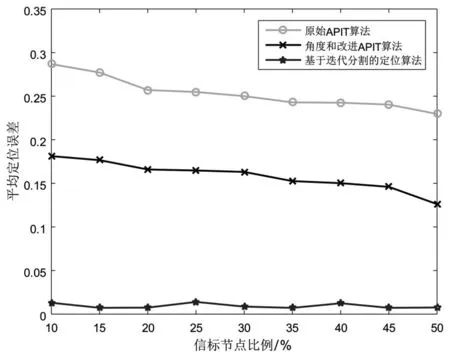
图10 节点比例与定位误差对比图

原始APIT算法和文献［13］利用角度和改进的APIT算法的平均定位误差随着信标节点比例的增加而减小。这是因为信标节点比例增加的同时，包含未知节点所在的三角形的重叠区域会随之减小，使得定位误差越来越小。如图10所示，基于迭代分割的无线传感器定位算法随着信标节点比例的增加，定位误差趋于稳定且一直保持较高的精度。因为基于迭代分割的无线传感器定位算法运用最小三角形迭代思想求出包含未知节点的最小区域代替原始算法中多个三角形的重叠区域。总之，两种改进算法的定位精度均高于原始APIT算法的定位精度，并且基于迭代分割的无线传感器定位算法的定位精度最高。

场景2：设定通信半径R=100，信标节点的个数为：anchors=nodes·ρ，ρ=0.3。平均运行50次，可得到如表2所示数据。

通过对实验数据表3的分析，得到待定位节点的平均定位误差和节点数量之间的关系，如图11所示。

图11 节点数量与定位误差对比图

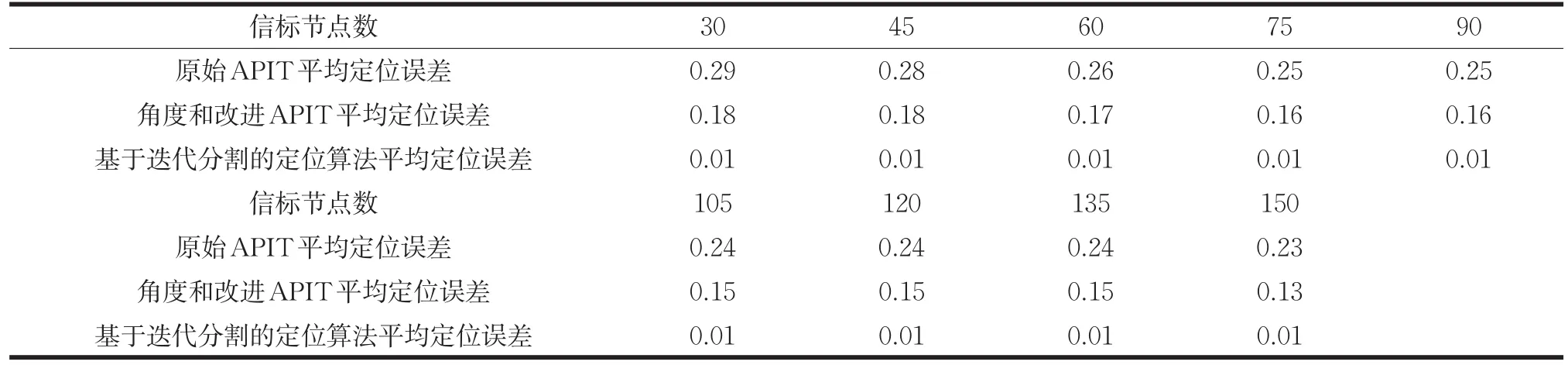
表2 实验数据

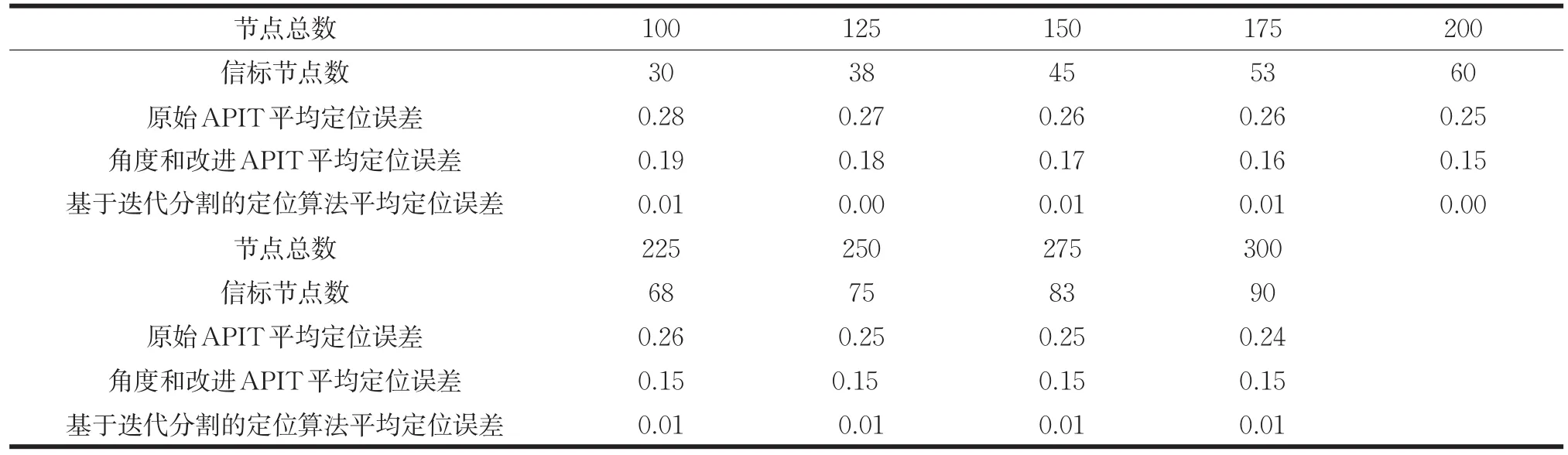
表3 实验数据

当信标节点比例不变时，随着区域内节点数量的增加，使得待定位节点邻近信标节点的数量不断增加，故节点的平均定位误差的变化趋势同样会随着节点数量的增加而减小。基于迭代分割的无线传感器网络定位算法的定位精度明显优于原始APIT算法和文献［13］利用角度和改进的APIT算法的定位精度。

通过场景1与场景2的比较分析，基于迭代分割的无线传感器网络定位算法的定位精度比利用角度和改进的APIT算法平均提高15.1%，较原始APIT算法平均提高24.6%。

4 结论

针对APIT定位算法存在的误差，基于迭代分割的无线传感器定位算法主要从两个方面进行了误差修正。首先，对于APIT算法存在的两种典型错误In-To-Out和Out-To-In错误，引入了一种新的判断内部节点的方法，该方法能够有效的避免上述两种错误的产生；其次，当未知节点被判定在三角形内部的情况下，利用迭代分割方法进一步缩小三角形区域，从而确定最终定位区域。通过上述两种方法进行了多次仿真实验，结果表明，基于迭代分割的无线传感器定位算法可有效降低定位误差，且当信标节点比例不高或者节点密度变大时能够保持算法的稳定性。