沥青质在渣油加氢催化剂中的扩散受阻
2019-11-22孙昱东韩忠祥
孙昱东, 陈 洁, 韩忠祥
(中国石油大学(华东) 化学工程学院,山东 青岛 266580)
渣油加氢过程中,沥青质分子需扩散进入催化剂内部,在催化剂内部的活性中心上与活性氢发生反应。研究表明,沥青质聚集体在催化剂中的扩散行为非常复杂,不仅与沥青质分子的尺寸有关,还和催化剂孔径尺寸、曲折性等性质有关[1]。为了研究沥青质分子在催化剂孔道中扩散时受到的阻碍作用与扩散分子大小和催化剂孔径尺寸的关系,研究者[2-4]多使用与两者有关的扩散受阻因子来表示沥青质聚集体在催化剂中扩散时的受阻程度,但目前主要集中在模型催化剂中的扩散受阻研究。
本文中笔者主要考察了不同实验条件下,沥青质大分子的甲苯溶液在不同孔径催化剂中的受阻扩散行为,并计算沥青质在催化剂中的受阻扩散参数。
1 实验部分
1.1 原料
实验原料为塔河常压渣油的正庚烷沥青质,所用溶剂为甲苯(化学纯,阿拉丁化学试剂有限公司产品)。沥青质20 ℃的密度为1170 kg/m3,平均相对分子质量7122(VPO-蒸汽压渗透法测定),氢/碳摩尔比1.05。甲苯20 ℃的密度为867 kg/m3,25 ℃的黏度5.9×10-4Pa·s,摩尔体积1.06×10-4m3/mol。
1.2 催化剂
扩散研究使用5种工业Al2O3基渣油加氢处理催化剂(均为中国石化齐鲁石化公司催化剂厂生产),催化剂内部特征不同,但外部特征相近,横截面均为直径约0.9 mm的四叶草形,轴向长度约10 mm,分别标注为A、B、C、D、E,基本性质如表1所示。催化剂的表面性质由美国Micrometrics生产的ASAP2010物理吸附仪测定。

表1 5种催化剂的性质Table 1 Properties of five catalysts
1.3 实验方法
实验前分别将催化剂放置于150 ℃的真空干燥箱中干燥3 h,结束后冷却至室温并称取一定质量的催化剂(使剂/油质量比为1/10),将催化剂置于盛有甲苯的烧杯中2 h,使催化剂孔道中充满溶剂,然后将多余的甲苯移除。
另量取200 mL甲苯溶剂置于三口烧瓶中,称取一定质量的沥青质加入溶剂中,使沥青质在溶液中的质量分数分别为0.2%、0.3%、1.0%、2.0%和3.0%。将盛有溶液的三口烧瓶放在100 ℃的恒温油浴锅中加热搅拌30 min,使沥青质完全溶解于甲苯中,然后放在25 ℃的水浴锅中恒温并不停搅拌。
将甲苯浸泡后的不同工业催化剂加入到盛有沥青质溶液的三口烧瓶中并开始计时,在常温(25 ℃)和常压下,实验进行480 min,每隔20 min取1次样品加入到1 cm石英液槽中,使用紫外-可见分光光度计在波长为750 nm条件下测定溶液的吸光度,进而计算溶液中沥青质的质量分数[5],考察沥青质聚集体在催化剂孔道中的扩散受阻情况。为了降低取出样品对后续实验结果的影响,每个具有不同孔径催化剂的扩散实验分6组进行,每组只取4次样,扩散实验结果见文献[5]。
2 结果与讨论
2.1 扩散受阻因子的计算
沥青质分子大小与加氢处理催化剂的孔径尺寸处于同一数量级,在催化剂中扩散时,孔壁与沥青质分子之间存在交互作用,催化剂孔道会阻碍沥青质的扩散,从而使沥青质分子的有效扩散系数降低。对于沥青质大分子在多孔催化剂中的有效扩散系数,可由式(1)计算[6]:
Deff=F(λ)D∞εp/τ
(1)
扩散受阻因子有不同的计算关联式,采用应用比较广泛的幂率经验关系式[7],即:
F(λ)=(1-λ)k
(2)
关联式(1)和式(2),得到沥青质分子在多孔催化剂中的限制性扩散受阻方程为:
F(λ)=(1-λ)k=Deffτ/D∞εp
(3)
将由扩散实验得到的估计参数及计算参数代入式(3),以Deff/D∞εp和1-λ的对数作图,可以得到一条直线,直线的斜率即为k,截距为lnτ,从而得到F(λ)。故可根据不同条件下的扩散实验数据,考察沥青质聚集体在加氢处理催化剂中的扩散受阻情况。
2.2 沥青质在不同催化剂中的受阻扩散
将不同初始浓度和不同孔径催化剂的扩散实验结果,根据前述数学模型拟合出相应的参数[5],整理得到不同实验条件下的λ和Deff/D∞εp等结果,见表2。
由表2可知:使用相同的催化剂时,随着沥青质在溶液中初始质量分数的增加,沥青质聚集体的动力学半径Rh增大,λ值增大;当溶液初始质量分数相同时,随着催化剂平均孔半径的减小,λ值增大。
表2中所有Deff/D∞εp的计算值均远远小于1,说明沥青质聚集体在催化剂孔道中的扩散性能小于在溶液中的扩散性能,即沥青质在催化剂孔道中的扩散受到限制。

表2 5种催化剂的扩散实验参数Table 2 Parameters of diffusion experiments for five catalysts
1)Deffandεpare the calculated values undert=0.
使用B、C、D催化剂时,Deff/D∞εp的数量级为10-2,比使用催化剂A时减小了1个数量级,说明沥青质聚集体在催化剂B、C、D中的扩散比在催化剂A中的扩散受到了更严重的阻碍作用。使用催化剂E时,Deff非常小,当溶液初始质量分数增加到1.0%时,Deff为8.8×10-13m2/s,比使用其他催化剂时减小了一个数量级,Deff/D∞εp的数量级为10-3,说明在催化剂平均孔半径为4.7 nm时,沥青质聚集体在催化剂孔道中扩散受到了严重的阻碍作用,不利于其在催化剂中的扩散。
随着催化剂孔半径的减小,相同溶液浓度的Deff/D∞εp数值有明显的降低,如溶液初始质量分数为0.2%时,当孔半径从12.5 nm减小到4.7 nm时,Deff/D∞εp从0.1512减小到了0.0135,减小的幅度非常大,进一步证明了催化剂孔径尺寸对沥青质聚集体的有效扩散影响非常大。
2.3 催化剂孔径对扩散受阻因子的影响
为了解催化剂孔径对沥青质聚集体扩散的受阻影响程度,根据式(3),将表2中的扩散数据Deff/D∞εp对1-λ作图,两者均采用对数坐标,如 图1 所示,则直线的斜率即为溶质分子扩散受阻程度的系数k,截距为曲折因子的对数lnτ。

图1 不同催化剂时Deff/D∞εp随1-λ的变化Fig.1 Variation of Deff/D∞εp with 1-λ for different catalysts
由图1可知:使用不同的催化剂时,Deff/D∞εp与1-λ的双对数变化关系均为一直线,且在坐标上的位置不同;催化剂孔径越大,相应的趋势线越接近坐标原点,而催化剂E的趋势线与其他催化剂的趋势线相离较远。
5种催化剂的趋势线均具有较好的线性关系,拟合得到5条直线的斜率k,并根据截距计算出催化剂的曲折因子τ,结果见表3。
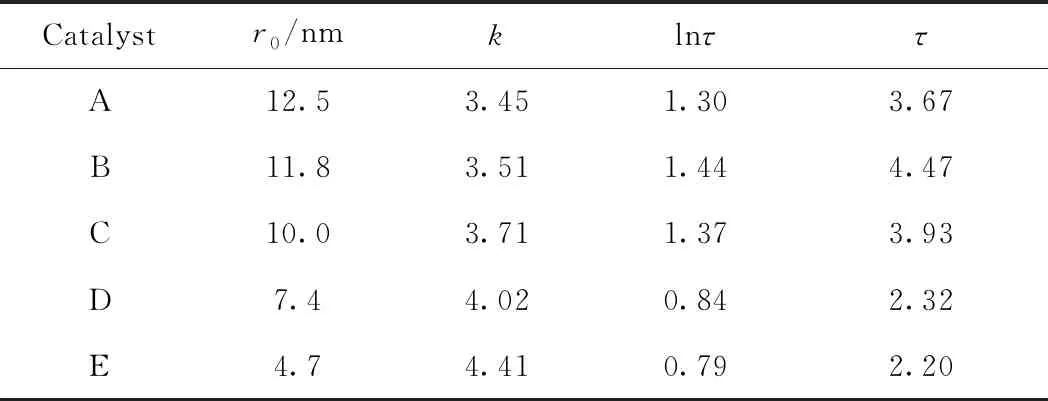
表3 Deff/D∞εp对1-λ的双对数趋势线拟合参数Table 3 Fitted data of the double logarithmicfor Deff/D∞εp with 1-λ
由表3可知,随着催化剂孔半径尺寸减小,k值增加,即沥青质聚集体在催化剂中扩散时的受阻程度增加。催化剂的曲折因子τ均在经验值2~7范围内,其中催化剂B的曲折因子最大。
将沥青质初始质量分数为0.2%时,使用5种催化剂进行扩散研究所得λ值代入式(3),得到沥青质聚集体在不同催化剂中的扩散受阻因子F(λ),见表4。
由表4可知,F(λ)均小于1,说明沥青质聚集体在5种催化剂中的扩散均为受阻扩散。扩散受阻因子F(λ)随催化剂孔半径的减小而降低,当催化剂孔半径从12.5 nm减小到4.7 nm时,F(λ)从0.4536减小到了0.0628,扩散受阻因子受催化剂孔径的影响非常大。当使用孔半径为4.7 nm的催化剂E进行扩散实验时,F(λ)值仅为0.0628,比使用其他催化剂时降低了一个数量级,说明沥青质聚集体在催化剂E中的扩散受到了严重阻碍。即随着催化剂孔径尺寸增加,沥青质聚集体在催化剂孔道中扩散的受阻程度减小,孔径越大越有利于扩散。
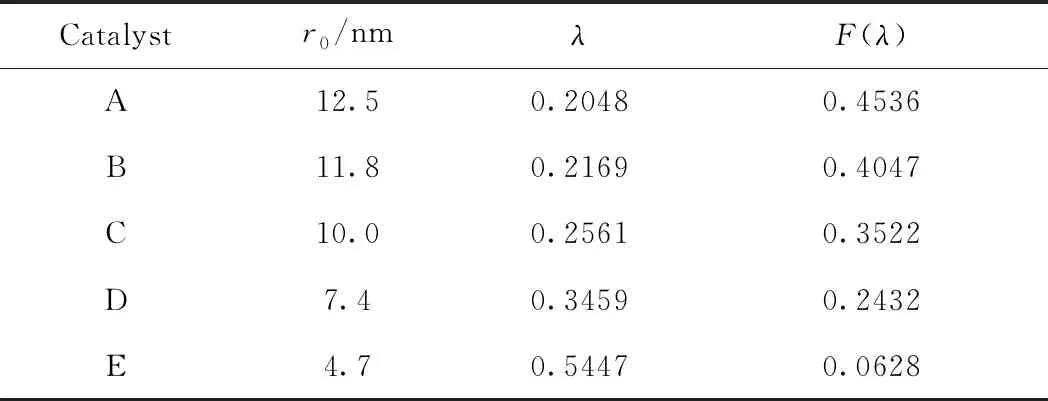
表4 沥青质在不同催化剂中的扩散受阻因子Table 4 Diffusion restrictive factors of asphaltenein different catalysts
w(Asphaltene)=0.2%
3 结 论
(1)沥青质聚集体在渣油加氢催化剂中为受阻扩散,其有效扩散系数和本相扩散系数的关系,可以采用受阻扩散因子表征。
(2)沥青质聚集体在不同孔径的催化剂孔道中扩散受阻情况明显不同。催化剂孔径越小,沥青质聚集体扩散时受阻碍作用越严重,扩散受阻因子F(λ)值越小,扩散阻力及扩散受阻因子受催化剂孔径的影响较大。
符号说明:
Deff——有效扩散系数,m/s;
D∞——本相扩散系数,m/s;
F(λ)——扩散受阻因子;
k——表示溶质分子扩散受阻程度的系数;
r0——催化剂平均孔半径,nm;
Rh——沥青质聚集体在甲苯溶液中的动力学半径,nm;
t——扩散时间,min;
w0(Asphaltene)——沥青质在甲苯溶液中的初始质量分数,%;
εp——催化剂孔隙率;
λ——沥青质分子动力学半径与催化剂孔半径的比值,即λ=Rh/r0;
τ——催化剂的曲折因子,指扩散物在催化剂中的实际扩散距离与扩散方向颗粒长度的比值(τ=xL/l),表示催化剂孔结构和曲折程度的结构参数。
