矩阵与其方幂相似的进一步讨论及应用

晏瑜敏，杨忠鹏，陈梅香，吕洪斌，余志拯

(1.莆田学院数学与金融学院，福建 莆田 351100；2北华大学数学与统计学院，吉林 吉林 132013； 3.厦门大学数学科学学院，福建 厦门 361005)

0 引 言

设Fn×n、F[x]分别表示数域F上的n×n阶矩阵、一元多项式集合，为复数域，In表示n×n阶单位矩阵.r(A)、Dk(A)、fA(x)和mA(x)分别表示矩阵A∈Fn×n的秩、第k阶行列式因子、特征多项式和最小多项式.设、+分别表示整数、正整数的集合.总约定n×n阶幂零矩阵本文不加特别说明，矩阵中没有写出的元素约定都是零.

2014年，第六届全国大学生数学竞赛预赛给出如下问题，为叙述方便标注为命题1：

命题1设n为给定的正整数，则对任意m，l∈+，存在n阶方阵X使得

(1)

第六届全国大学生数学竞赛组委会为命题1提供的答题要点可整理为：

1) 所求的方程变为

(2)

其中f1(a1)由a1确定，…，fn-2(a1，…，an-2)由a1，…，an-2确定.

3)观察方程组

(3)

直接可看出该方程组(3)有解.

张福振在文献[1]中给出：

命题2([1，问题3.4.19]) 如果矩阵A的所有特征值都是1，则对任意正整数k，总有Ak与A相似.

命题2是很有影响的问题，丘维声教授的“高等代数”将其作为习题([2，习题6.11.21])，也是2010年新疆大学考研试题([3，例8.5]).

文献[4，例8.12]，[5，例12.4]，[6，例8.2.28]，[7，题3.11]都采用了命题2，在叙述上有些不同：设方阵A的特征多项式fA(x)=(x-1)n，则对任意自然数k总有Ak与A相似.从解答上看文献[4-7] “自然数”与文献[1-3]的“正整数”的意义相同.1993年国家颁布的《量与单位》(GB 3100～3102—93)规定自然数包括0(见文献[8]).这样看来文献[1-3]对命题2的叙述是准确的.

在李尚志的《线性代数(数学专业用)》有:

命题3(见[9，习题7.4.5]) 求证：方阵A与所有的Ak(k为正整数)相似⟹A的特征值全为1.

我们首先证明如果矩阵A的所有特征值都是1，则对任意非零整数k，总有Ak与A相似，那么由此可得到矩阵A与所有的Ak(k∈+)相似的充分必要条件.应用这些讨论的结论和方法，证明了可概括命题1的更广泛的一类非线性矩阵方程解的存在性.

1 预备知识

引理1设λ(≠0)∈F，则λIn+Hn可逆且

(4)

证明：由文献[10；11，引理1]知

(5)

从式(5)有

由此得式(4).证毕.

显然式(4)与文献[12，(1)]等价.从文献[13，问题3.4.3]知，当A，B∈Fn×n时，A，B在数域F上相似⟺A，B在复数域上相似.这样下面讨论(除非特殊说明)都在复数域上进行.

引理2([13，定理3.3.6]) 设A∈n×n所有不同的特征值为λ1，λ2，…，λt，则其中ki为A的Jordan标准形中由特征值λi确定的Jordan块的最高阶数.

从文献[9，定理6.4.3]及其说明可得：

引理3设A，B∈Fn×n，则A，B相似⟺A，B的行列式因子Dk(A)=Dk(B)，k=1，2，…，n.

引理4设m(≠0)∈(即m为非零整数)，则存在qm(x)=1+mx+a2x2+…∈[x] ，使得

(6)

证明：从In与Hn可交换知，当m∈+时，应用二项式定理展开，由式(5)得即有qm(x)=1+mx+a2x2+…∈[x]，使(In+Hn)m=qm(Hn)，即此时式(6)成立.

对任意负整数m=-s(s∈+)，从式(4)知存在g(x)=1-x+…+(-1)kxk+…+(-1)n-1xn-1∈[x] ，使得

(7)

由式(7)知有qm(x)=[g(x)]s=[1-x+x2+…+(-1)txt+…+(-1)n-1xn-1]s，即

qm(x)=[g(x)]s=1-sx+a2x2+…=1+mx+a2x2+…∈[x].

(8)

对任意s=(-m)∈+，由式(4)，(7)和(8)得(In+Hn)m=[(In+Hn)-1]s=[g(Hn)]s=qm(Hn)，即知此时式(6)成立.证毕.

引理5设A∈n×n，如果对任意k∈+总有fAk(λ)=fA(λ)，则A的不同特征值为0或1.

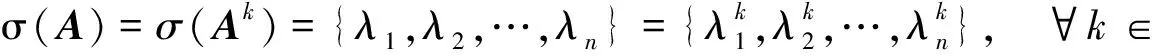
引理6([11，定理2]) 设A∈n×n，则下述命题等价：

ⅰ)r(A)=u(A)(A的非零特征值的个数)；

ⅱ)mA(x)=h(x)或mA(x)=xh(x)，这里首1多项式h(x)满足h(0)≠0；

ⅲ)r(A)=r(A2).

2 矩阵A与Ak相似的进一步讨论

定理1设A∈n×n的所有特征值都是1，则对任意k(≠0)∈总有Ak与A相似.

证明：由A的所有特征值都是1，知有可逆矩阵P使得

P-1AP=diag(J1，J2，…，Js)=JA，Ji=Ini+Hni，i=1，2，…，s，

(9)

由式(9)知

Dni-1(Ji)=…=D1(Ji)=1，Dni(Ji)=(λ-1)ni.

(10)

当k(≠0)∈时，由式(6)，(7)有

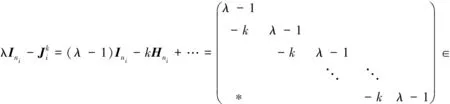
(11)

即对任意非零整数k总有Ak与A相似.证毕.

例1设A=diag(Ir，0)∈n×n，即A的特征值不全为1，从A=Ak知A与所有的Ak(k∈+)相似.这说明命题3未必总是正确的.

定理1表明命题2的结论对任意非零整数都成立.实际上文献[9，习题7.4.4]在2006年就提出了这样的问题.

推论1设A∈n×n，如果对任意k∈+总有Ak与A相似，则A的不同特征值为0或1，且A的Jordan标准形中由特征值0所确定的Jordan块都是一阶的.

证明：从对任意k∈+总有Ak与A相似，知有fAk(λ)=fA(λ)，∀k∈+.由引理5即得A的不同特征值为0或1.

设A的Jordan标准形JA，满足：

P-1AP=JA=diag(J1，J2，…，Jt，Jt+1，…，Js)， 其中P∈n×n可逆；

(12)

Ji=Hni，i=1，2，…，t；n1≥n2≥…≥nt，n1+n2+…+nt=n0；

(13)

Jj=Inj+Hnj，j=t+1，t+2，…，s.

(14)

当n0∈+，即n1∈+时，由式(5)和式(12)～(15)得

(15)

由于对任意k∈+总有Ak与A相似，应用式(12)～(15)可知特征值0(如果存在的话)确定的Jordan块都是一阶的.证毕.

从推论1及其证明可知，命题3可在保留前提条件下修改为：

推论2设A∈n×n，如果对任意k∈+总有Ak与A相似，则A的不同特征值为0或1.

也可保留命题3的结论修改为：

推论3设A∈n×n可逆，如果对任意k∈+总有Ak与A相似，则A的特征值全为1.

与命题3相对照，推论1较完整地讨论了张福振提出的命题2的逆问题.

许以超在文献[14-16]中都有与上述讨论相关的问题：

命题4([14，习题13.3.11；15，习题13.2.10；16，习题6.4.11]) 设矩阵A的特征值都等于1，试证：A和A的任意方幂都相似.

因为A的零次方幂为单位矩阵，可知命题4可按定理1的方式叙述.

从推论1的证明和式(12)～(14)知，当对任意k∈+总有Ak与A相似时，A满足

P-1AP=JA=diag(0n0，Int+1+Hnt+1，…，Ins+Hns).

(16)

反之，当A满足式(16)时，仿照定理1的证明可知，对任意k∈+总有Ak与A相似.这样作为命题2及其逆问题，应用推论1可得到：

定理2设A∈n×n，则对任意k∈+总有Ak与A相似⟺A的不同特征值为0或1，且特征值0确定的Jordan块都是一阶的⟺A的Jordan标准形由式(16)确定.

由式(16)知，对任意k∈+总有Ak与A相似的矩阵，满足矩阵秩与非零特征值个数相等.从定理2和引理6可得到：

定理3设A∈n×n，则对任意k∈+总有Ak与A相似⟺r(A)=u(A)且非零特征值全为1⟺r(A)=r(A2)且所有非零特征值全为1⟺mA(x)=xl(x-1)n-l，0≤l≤1.

设A∈n×n，如果有A#∈n×n使得AA#A=A，A#AA#=A#，AA#=A#A，则称A∈n×n是群可逆的，并称A#为A的群逆，此时也称A为GP矩阵.从文献[1，17-18] 知不是每个矩阵都为群可逆的，当然GP矩阵的群逆是唯一的.这样从文献[10-11]和定理3可得到：

推论4设A∈n×n，则对任意k∈+总有Ak与A相似⟺A为非零特征值全为1的GP矩阵.

3 一类非线性矩阵方程解的存在性

定理4设n与k(≥2)为给定的正整数，下三角矩阵G=(gij)∈n×n满足gii=k-1，i=1，2，…，n，且对任意非零的m1，m2，…，mk∈，如果m1+m2+…+mk≠0，则存在X∈n×n使得

Xm1+Xm2+…+Xmk=In+G.

(17)

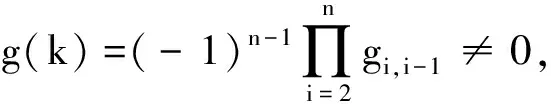
Dn(A)=(λ-k)n，Dn-1(A)=Dn-2(A)=…=D1(A)=1.

(18)

设Y=In+Hn，则Y可逆且对任意m(≠0)∈来说，Ym=(In+Hn)m=In+mHn+…，这样可令B=Ym1+Ym2+…+Ymk，对任意非零的m1，m2，…，mk∈.从引理4知

(19)

由式(19)得Dn(B)=(λ-k)n.由λIn-B的第2，3，…，n行与第1，2，…，n-1列构成的子式

从h(k)=(-(m1+m2+…+mk))n-1≠0知Dn-1(B)=1，进而由式(18)知A与B有相同的行列式因子.这样应用引理3知

P-1BP=P-1(Ym1+Ym2+…+Ymk)P=A， 存在可逆矩阵P∈m×m.

(20)

令X=P-1YP=P-1(Im+H)P，从引理4和式(20)知Xn1+Xn2+…+Xnk=P-1(Ym1+Ym2+…+Ymk)P=A，这就证明了矩阵方程(17)的解是存在的.证毕.

显然命题1是定理4中取gi，i-k=k+1，k=1，2，…，n-1，2≤i≤n，m1，m2∈+的特例，由此可得命题1的新证法.定理4中“下三角矩阵G=(gij)∈m×m满足gii=k-1，i=1，2，…，m，且要求的条件比命题1宽松得多.此条件下式(17)的右边的已知矩阵要表示成像式(2)那样的Hn的多项式不是容易的事，因此要得到形如(3)的方程组是很困难的.

由上可知，定理4及其证明就是将命题1及其证明推广应用到k≥2的情形.