n×n矩阵空间的幂等基与对合基
2019-11-22苏茹燕杨忠鹏陈梅香
苏茹燕,杨忠鹏,陈梅香
(1.莆田学院数学与金融学院,福建 莆田 351100;2.福建师范大学数学与信息学院,福建 福州 350001)
0 引 言


作为一般情况Pn×n是否有由幂等矩阵构成的基(简称幂等基)?如果有幂等基,那么就会有与文献[8]相同的思考方向,即每个n×n阶矩阵可被幂等矩阵线性表示.由一个向量能被一组向量唯一地线性表示的充要条件是这组向量线性无关(见文献[10,例4.9]),可知Pn×n幂等基的存在,可从另外的角度证明n×n阶矩阵可由n2个幂等矩阵唯一线性表出.
文献[11]对K.Hoffmon等的疑问给出正面的回答,证明了Pn×n存在幂等基;文献[12]用文献[11]的方法讨论特征为零的域上K-幂等基的存在性.
对合矩阵也是常用矩阵类(见文献[13-14]).是否有与K.Hoffmon等疑问类似的由n2个对合矩阵构成的Pn×n的基(简称对合基),这也是一个有趣的问题.
本文在得到幂等基的基本性质的基础上,给出了为区别不同幂等基之间差异的“基秩”定义,得到了Pn×n的所有幂等基的基秩的最大值和最小值分别为n2(n-1)+1和n2.我们用不同于文献[11-12]解答K.Hoffmon等疑问时幂等基的构造方法,得到P2×2的对合基.同时证明n≥3,Pn×n存在着由n2个对合矩阵构成的基.
1 预备知识
由矩阵乘法易得
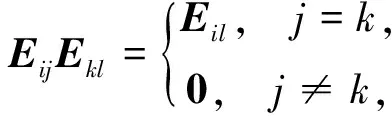
(1)
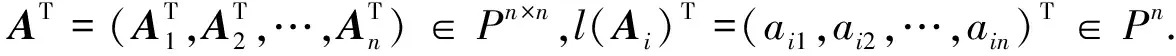
引理2设Iij∈Pn×n,i,j=1,2,…,n,且约定
(2)

(3)

由定义1知
(4)


由文献[15,problems 5.1.8]可得:
引理4设A∈Pn×n,则A2=A⟺B2=E,其中B=2A-E.
引理5设A∈Pn×n,则
r(A)+r(A-E)=n+r(A2-A),
(5)
A2=A⟺(E-A)2=E-A.
(6)
2 Pn×n矩阵空间幂等基性质

(7)
证明:由式(2)知
(8)
由式(8)可得
(I11,I12,…,I1n,I21,I22,…,I2n,…,In1,In2,…,Inn)=
(E11,E12,…,E1n,E21,E22,…,E2n,…,En1,En2,…,Enn)H.
(9)
由式(9)知式(7)成立.证毕.

(10)
即
(11)
这样由式(7)、(8)得
(E11,E12,…,E1n,E21,E22,…,E2n,…,En1,En2,…,Enn)=
(I11,I12,…,I1n,I21,I22,…,I2n,…,In1,In2,…,Inn)H-1,
即

(12)
从引理1和式(11)、(12)可知式(9)成立.证毕.
定理2表明任意A=(aij)∈Pn×n都可唯一表示为由式(2)、(3)所表示的标准幂等基的线性组合,且可用式(10)显示线性表出系数,与文献[8]不同之外,还在于我们的线性表示是唯一的.


(13)
(3)积极创新融合发展新模式新业态 制造业、互联网、物流、金融等领域企业应面向变革生产模式、创新交易方式、破解融资难题等制造业关键领域,积极开展网络化协同研发制造、大规模个性化定制、服务型制造等“制造业+互联网”新模式的应用,并围绕工业电子商务、产融结合等重点方向积极创新融合发展新模式,促进我国制造业价值链全面升级,从而实现经济高质量发展。

(14)
r(Gij)=n-r(Iij)=n-1,i≠n且j≠n;r(Gnn)=n.
(15)

(16)
由式(14)、(16)得
即
(17)
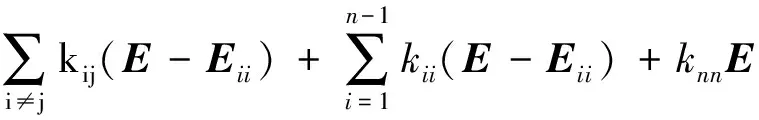
即此时式(16)简化为
(18)
式(18)说明式(16)等价于以k11,k22,…,knn为变量的齐次线性方程组
(19)


3 Pn×n矩阵空间的对合基

定理4说明,由引理4知可从标准幂等基得到4个不同的对合矩阵,但它不能成为P2×2的对合基.相对K.Hoffmon等提出的P2×2的幂等基和定理4我们自然要问P2×2是否存在对合基?
定理5P2×2存在对合基.

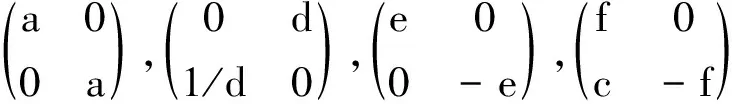
虽然无法应用解决K.Hoffmon等疑问中的标准幂等基得到P2×2的对合基,但定理5证明P2×2存在对合基.定理4的情况在n≥3时会怎样?如果也要像通过定理5那样,来构造Pn×n的对合基,无疑随着n的增大计算量会增加很大.
定理6设n为任意正整数,当n≥3时,Pn×n存在如下确定的对合基
(20)

(21)
由式(20)、(21)得
即
(22)

(23)
与定理3的证明类似,易知式(23)与下面齐次线性方程组等价
(24)


从基秩的定义、引理2和推论1可得:

