一类常微分方程第二特征值的研究

吴 平

（苏州市职业大学 数理部，江苏 苏州 215104）

1 问题的提出

本研究将文献[1]所讨论的常微分方程进行推广，得到如下的此类常微分方程的普遍形式，即：

其中c1和c2为任意的正常数。c1=c2=1的情况已在文献[1]中进行了研究，因此文献[1]中的方程是方程（1）的特例，方程（1）是文献[1]、文献[2]中方程的推广。当λ是方程(1)的特征值时，可基于文献[1]和[2]中的方程及研究思路研究其第一特征值1λ和第二特征值2λ的关系。

设u1，u2为正常数，u1≤u2, 并且

设1λ是方程(1)的第一特征值，对应的特征函数为y，则满足

由文献[2]的式（3）和分部积分法，可得

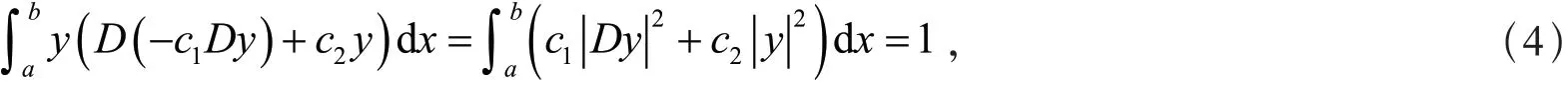
由分部积分法和式（4），可得

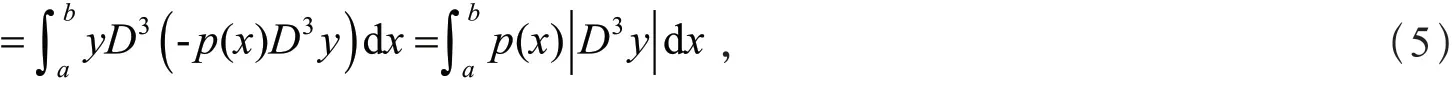
由式（2）和式（5），可得

则利用分部积分，可求得

由t的定义及式（4），可得式（7）等于0，即

由式（8）可知，ϕ与y广义正交，并且满足

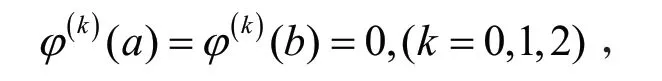
由文献[1]的式（2.6）和Rayleigh定理 ，可得方程（1）的第二特征值2λ满足

计算得

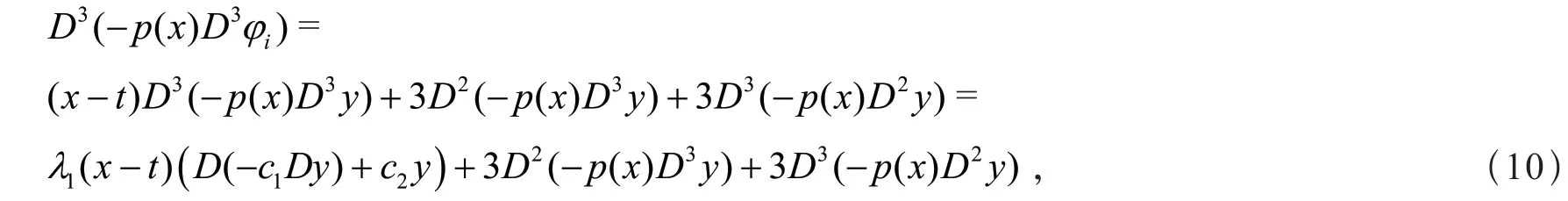
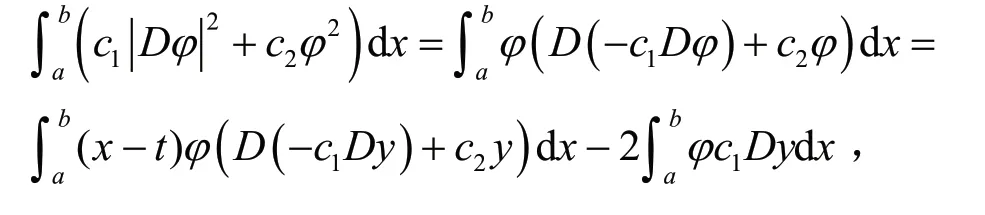
即

由式（10）和式（11），得

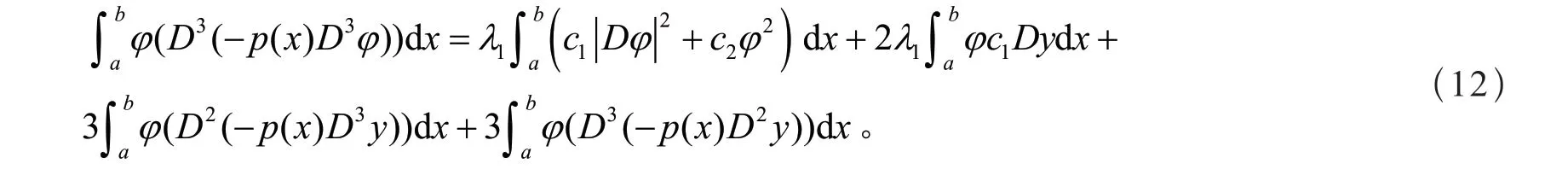
设

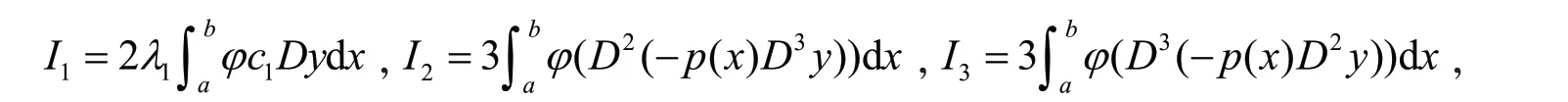
由式（12），得

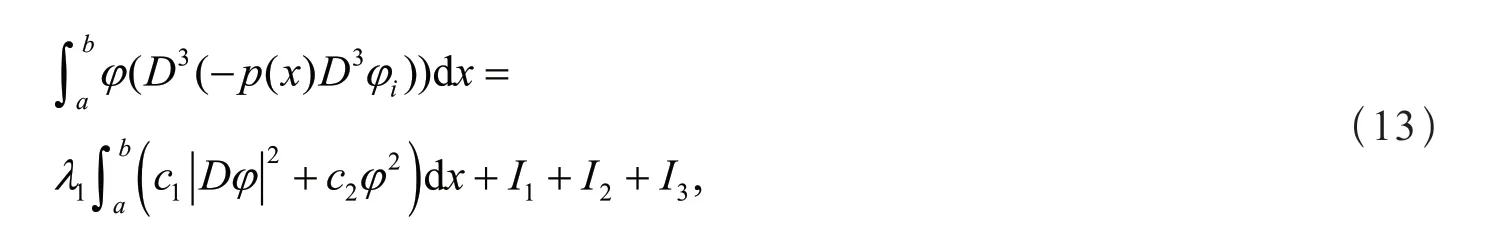
由式（9）和式（13），得

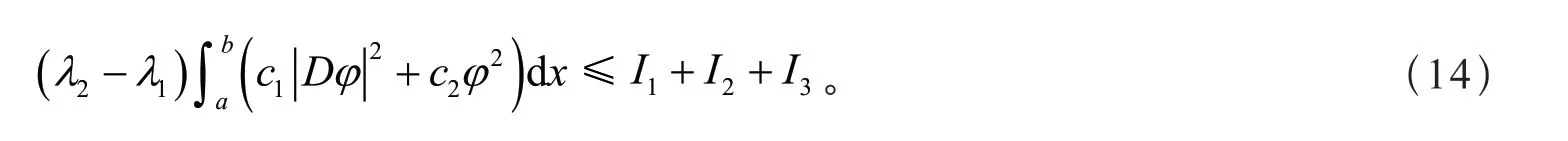
2 引理

为了证明方程（1）的第一特征值1λ和第二特征值2λ的关系，必须先证明下面的引理。本研究将文献[3]中引理的证明方法作进一步推广。

引理1若y是方程（1）对应的第一特征值1λ的特征函数，则

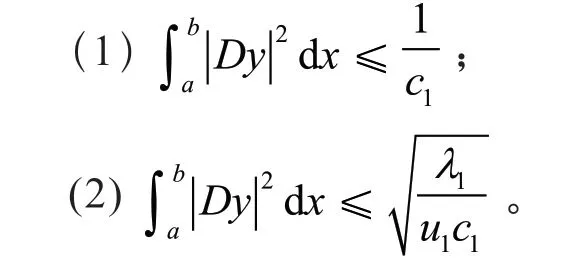
证明 由式（4），可得引理1（1）；

由分部积分，Schwartz不等式，式（6）和引理1（1），可得

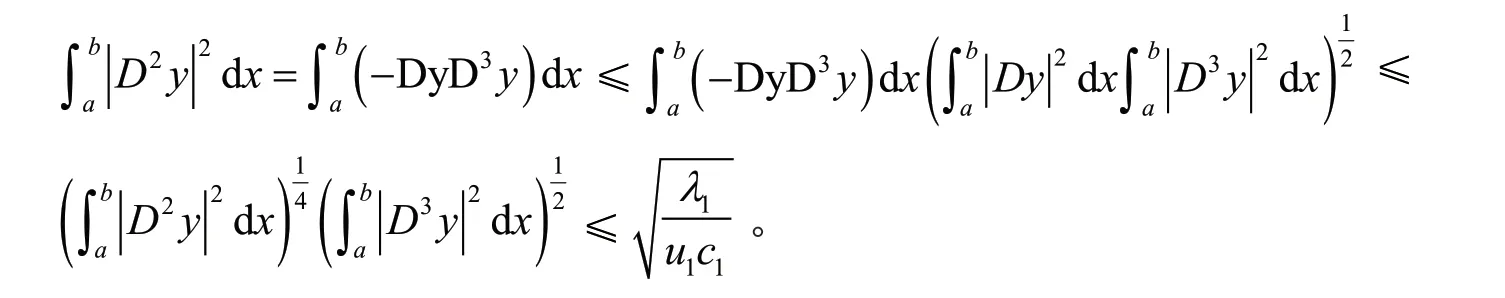
引理2若y是问题（1）对应的第一特征值1λ的特征函数，则

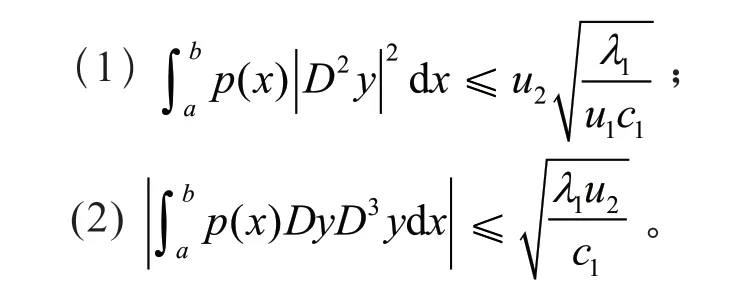
证明 由文献[3]的引理2（a) ，式（2）和引理1（2），得

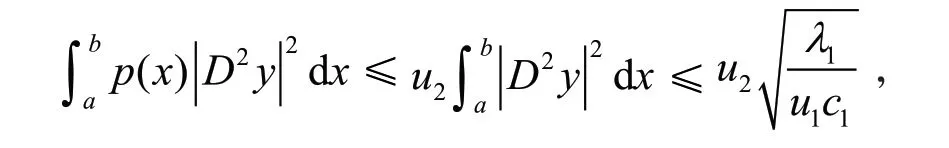
则引理2（1）得证；

由文献[3]的引理2（b) ，式（2），式（5) ，引理1和Schwartz不等式，得

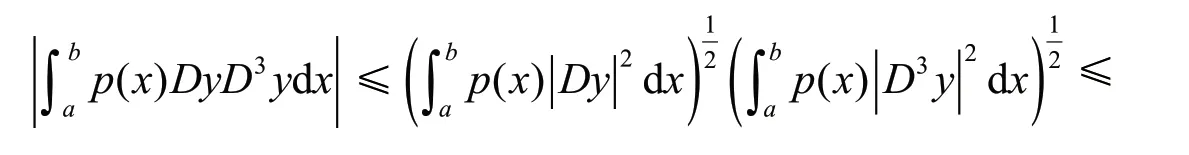
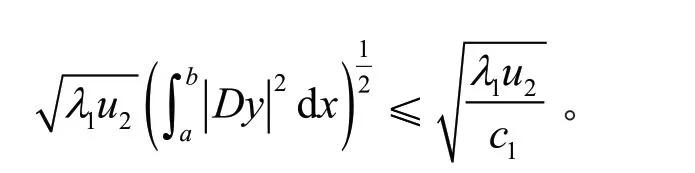
引理3若1λ为方程（1）的第一特征值，则

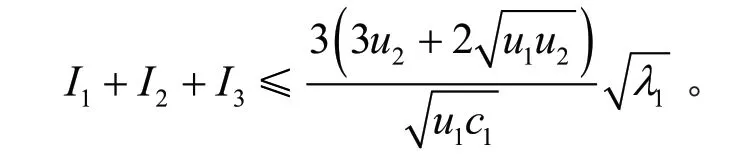
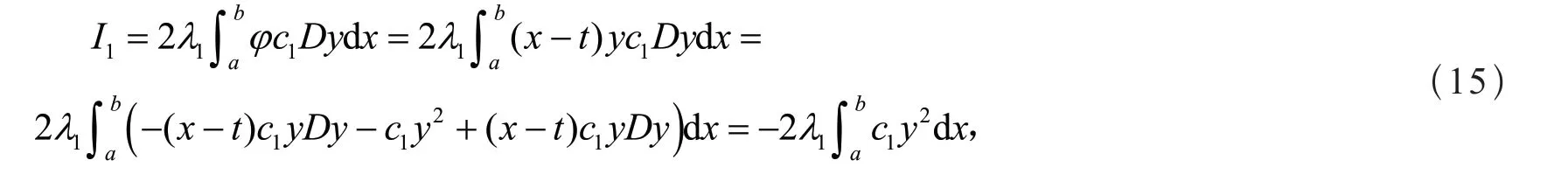
同理，可得

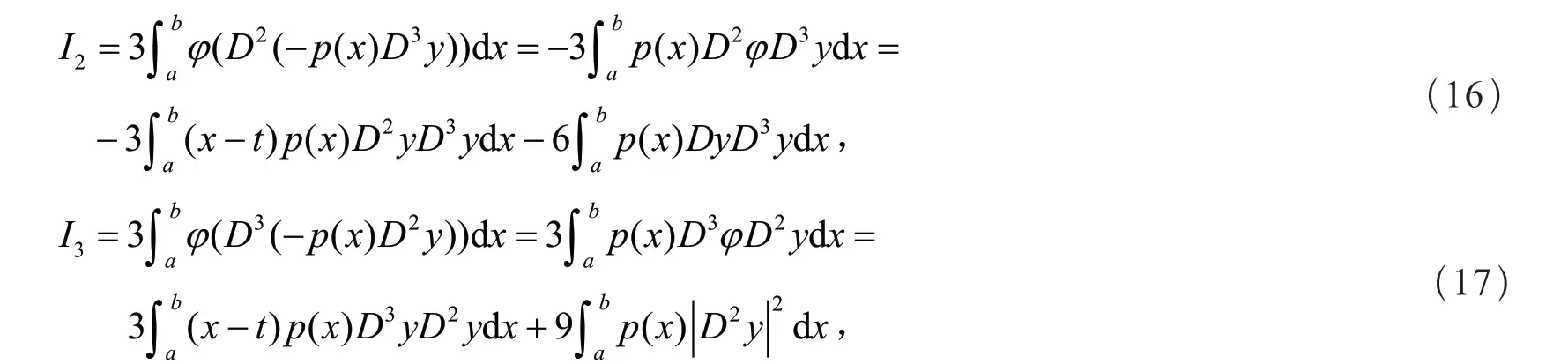
由式（15），式（16）和式（17），得

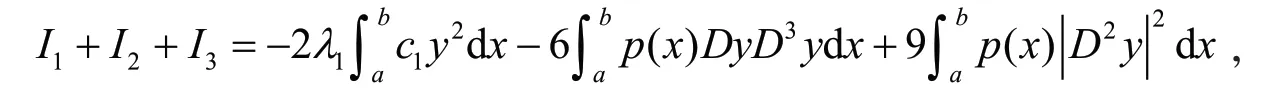
由式（15）和引理2，得

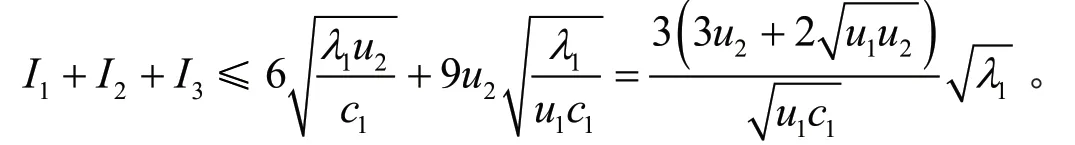
引理4对ϕ和1λ，则有

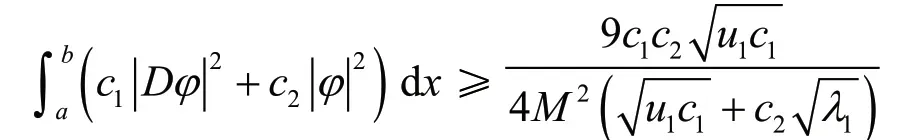
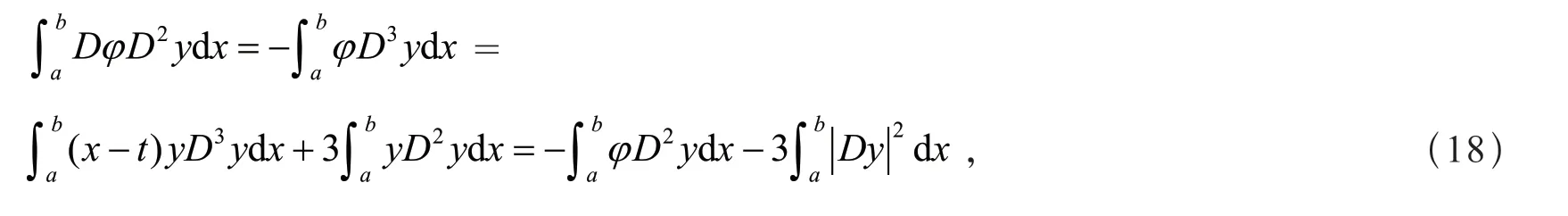
由式（18），得

同理，可得

由式（19）和式（20），得

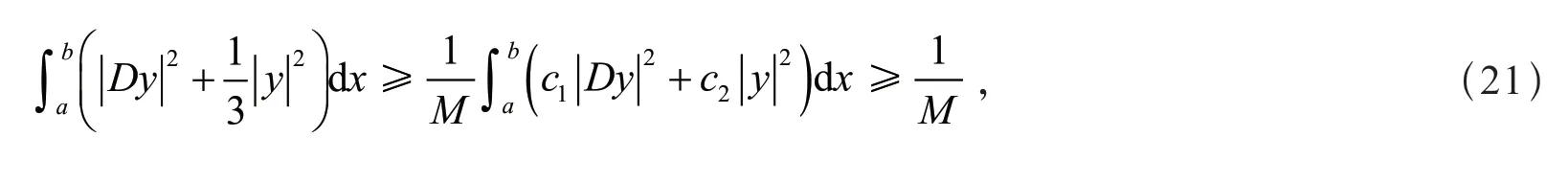
由式（19）～式（21），引理1和Schwartz不等式，得

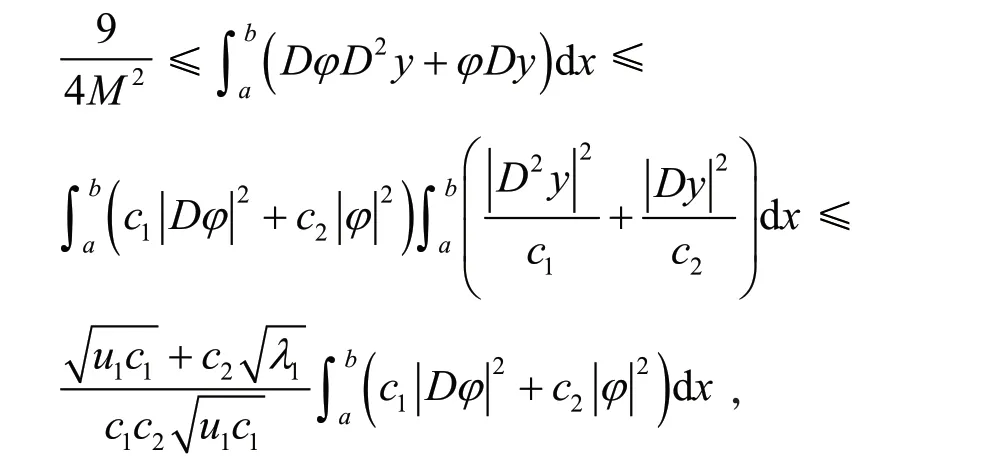
整理即得引理4。

3 结论

因本研究中的定理及其证明方法是文献[3]中定理及证明方法的推广，故借鉴文献[3]中定理的证明方法来研究方程（1）的第一特征值1λ和第二特征值2λ的关系。

定理设1λ、2λ分别是方程（1）的第一、第二特征值，且0＜1λ≤2λ，则有

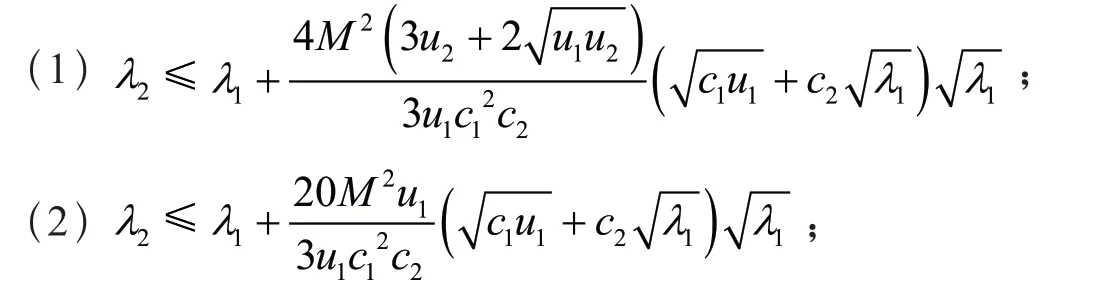
证明 由文献[3]的式（4），引理3，引理4和式（14），可得定理（1）；用u1替换u2，即得定理（2）。

常微分方程特征值的关系是数学学科研究的一类重要问题，本研究探讨了一类更为普遍的常微分方程，对其特征值的关系做了分析和研究，得到了其第一特征值和第二特征值之间关系，相关结论在常微分方程特征值的研究有着重要作用，在力学等物理学领域也有着广泛应用。