NSD序列加权和的若干收敛性及其在回归模型中的应用

何其慧

（安徽经济管理学院基础教学部，安徽合肥230059）

随机变量加权和的收敛性对统计模型中估计量的相合性的建立有非常重要作用。因此，研究随机变量加权和的收敛性质是非常有必要和有意义的。假设{ ani,1≤i ≤n,n ≥1 }为一常数阵列，满足

其中α ＞0。在这一假设下，很多学者建立了独立场合下的极限定理[1-4]。在相依场合下，文献[5]利用负相协（NA）随机变量的指数不等式将独立条件下的结果进行了推广。

定理A令r ＞1,1≤p ＜2,p ＜α ＜rp，为一同分布的NA 随机变量序列并满足EX =0,E|X|(r-1)β＜其中β满足假设常数阵列满足（1）式，则对任意的ε ＞0，都有

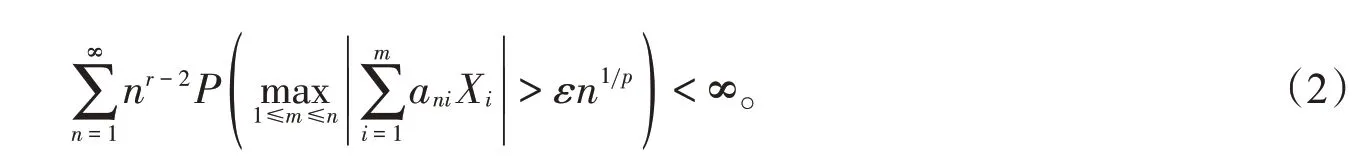
文献[6]在α ＞rp及EX=0,E|X|rp＜∞的条件下将（2）式推广到ρ*-混合序列。本文将在α ＞rp及EX =0,E|X|rp＜∞的条件下将定理A的结果推广到负超可加相依（NSD）随机变量序列，并且在相同的条件下进一步得到完全矩收敛性的结果，另外，还得到NSD序列加权和的强大数律。作为主要结果的应用，建立NSD误差下非参数回归模型中加权估计量的强相合性，所得结果亦改进了文献[7]的相关结果。本文用C 代表正的常数，在不同的地方可以取不同的值；I(A)为事件A 的示性函数；a+=aI(a ≥0)且a-= -aI(a ＜0)。

1 相关定义、引理

定义1[8]称随机变量是NA 的，如果对{ 1,2,…,n }的任意非空不交子集A 与B 都有其中f1与f2是使上式有意义且对各变元单调非降的函数。若对≥2,X1,X2,…,Xn是NA的，则称随机变量序列是NA的。

定义2[9]随机向量(X1,X2,…,Xn)称为NSD的，如果其中X1*,X2*,…,Xn*相互独立且对每个1与Xi有相同的分布是使得上式期望存在的超可加函数。如果对任意n ≥1，(X1,X2,…,Xn)为NSD的，则称随机变量序列是NSD的[10-12]。

定义3[13]称随机变量序列完全收敛于一个常数C，如果对任意的ε ＞0，都有

定义4[14]设随机变量序列则称为完全矩收敛于0。

引理1[9]设随机变量为NSD。若为单调非降（或非增）函数序列，那么仍为NSD。

引理2[9]令是均值为0的NSD随机序列。若存在q ≥2使得对所有的i ≥1都有则

2 定理及证明

定 理1令r ≥1,1≤p ＜2,α ＞rp，为 一 同 分 布 的NSD 随 机 变 量 序 列，且 满 足假设常数阵列满足（1）式，则对任意的ε ＞0,（2）式成立。

证明由于ani=故不失一般性，设ani＞0。由不等式，对任意的0 ＜s ＜α,都有对给定的n ≥1及1≤i ≤n，记

由引理1可知，{ Yni(1),1≤i ≤n,n ≥1 }仍然是NSD随机变量。易见

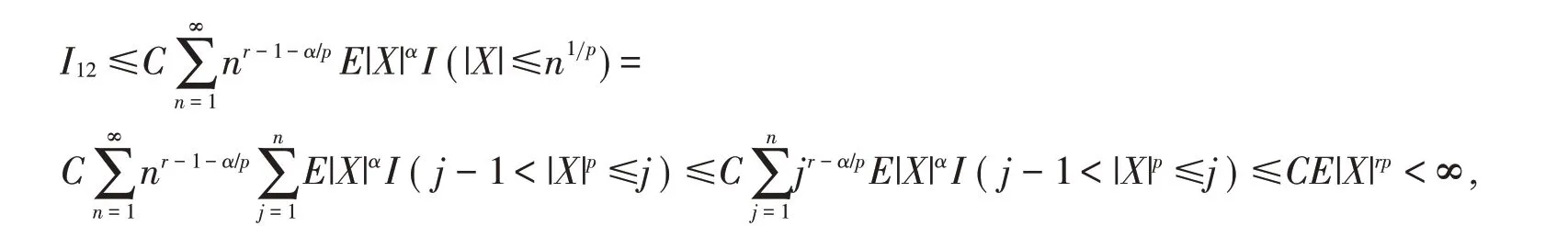
从而I1＜∞得证。对于I2，先证明事实上，由零均值的假设，以及控制收敛定理，可得

从而当n充分大时，对任意的ε ＞0，都有

下面证明I2＜∞。假设r ＞1，取q ＞其中p ＜s ＜min则由(3)式、Markov不等式、引理2、Cr不等式及Jensen不等式，可得

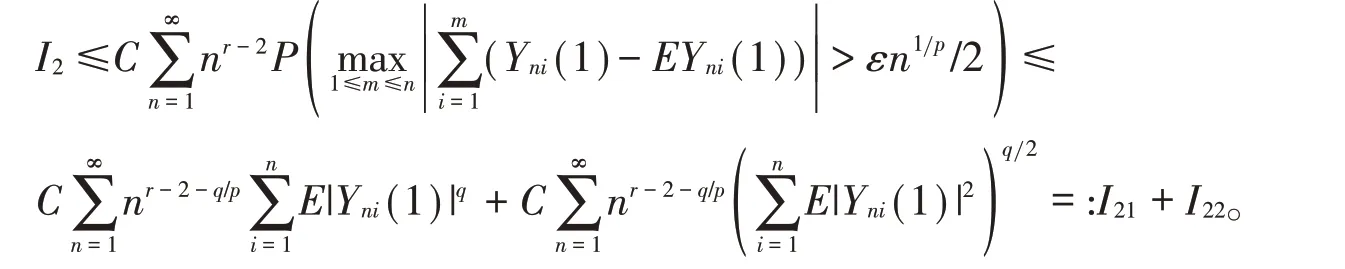
由Yni（1）的定义可知由的证明可知取0 ＜t ＜rp，可以验证

下面证明I22＜∞。注意到等

若r=1，则始终都有α ＞p=rp。因此，不失一般性，假设p ＜α ＜2，类似r ＞1 的证明，取q=2,即有当r=1时，证明过程类似I21，可证I2＜∞。

定理2令r ≥1,1≤p ＜2,0 ＜τ ＜rp ＜α为一同分布的NSD 随机变量序列，且满足EX=0,E|X|rp＜∞。假设常数阵列满足(1)式，则对任意的ε ＞0,有

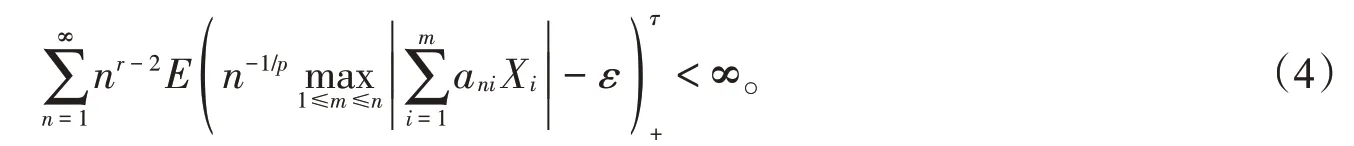
证明这里仍不失一般性地假设ani＞0。注意到

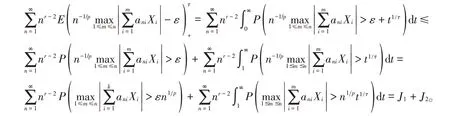
由定理1可得J1＜∞。因此要证明(4)式，只需要证明J2＜∞。对任意t ≥1，记

同样由引理1可知，{ Zni(1),1≤i ≤n,n ≥1 }仍然是NSD随机变量。易得

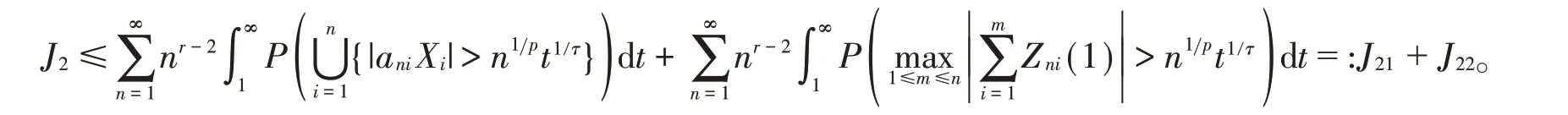
类似I1的证明，可得

对于J22，先证明由零均值的假设，|ani|≤Cn1α,E|X|p＜∞以及控制收敛定理，可得

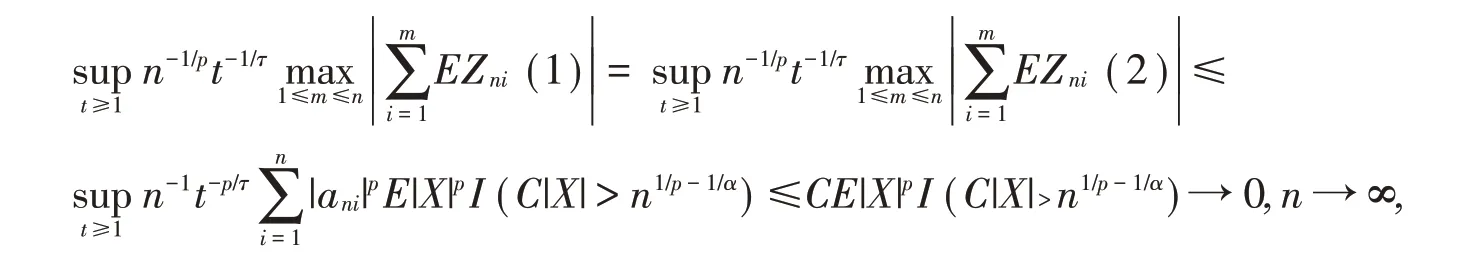
因此当n充分大时，对任意的t ≥1都有

类 似 定 理1 中I2的 证 明，同 样 先 考 虑r ＞1 的 情 况，取p ＜s ＜min及q ＞max由(5)式、Markov不等式、引理2、Cr不等式及Jensen不等式可得

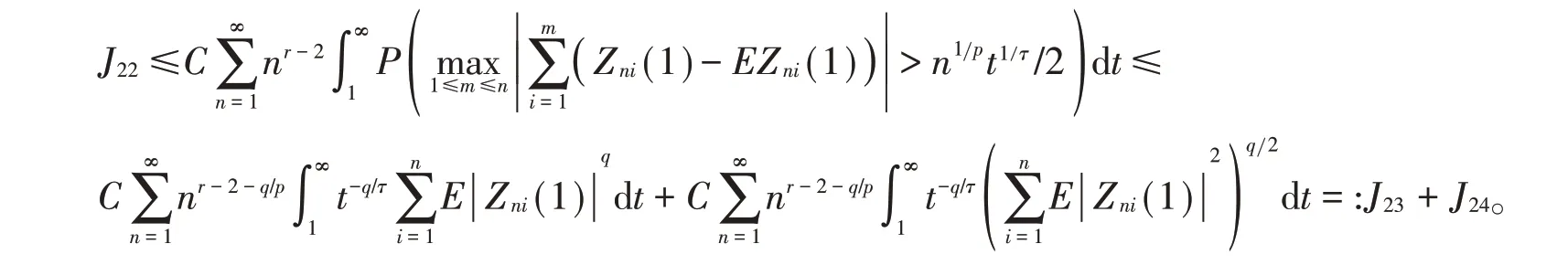
由J21的证明可得

由J21的证明，可得

类似地，若r=1，则有α ＞p=rp。因此，同样可以假设p ＜α ＜2，类似r ＞1 的证明，取q=2，即有完全类似J23的证明，可证明在r=1的情况下也有J22＜∞。

注1注意到

由ε ＞0的任意性可知，定理2是比定理1更强的结果。

定理3令1≤p ＜为一同分布的NSD随机变量序列，且满足EX=0,E|X|p＜∞。常数列满足其中α ＞p，则

证明在定理1中取r=1,ani=ai，可得

下面给出定理1的一个应用。

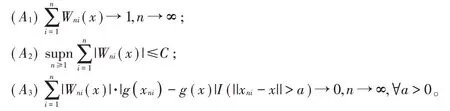
定理4假设条件(A1)～(A3) 成立。令为 同 分 布 的NSD 随 机 误 差，使 得

证明类似文献[12]中(3.7)式的证明，可以由条件(A1)～(A3)推出故只需证明在定理1 中取其中1≤i ≤n,n ≥1，即可得证。

注2 文献[7]也建立了NSD 误差下的相应结果，其中需要的条件为及由柯西不等式知故 上 式 成 立 只 能 取p ＞1。 注 意 到及定理4中p可以取到1，所以定理4改进了文献[7]的结果。

3 结 论

本文利用NSD随机变量的极大值矩不等式及截尾方法，建立了NSD序列加权和的完全收敛性、完全矩收敛性及加权和的强大数律，推广并改进了相关文献的结果，具有一定的理论价值和实际意义。作为应用，本文得到了NSD误差下非参数回归模型估计量的强相合性，此结果也改进了相应文献的结果。