对偶平坦球对称Finsler度量的构造

耿 杰，宋卫东，郑家耀

（1.安徽信息工程学院通识教育与外国语学院，安徽芜湖241000；2.安徽师范大学数学与统计学院，安徽芜湖241000）

Finsler几何有着悠久的历史，在微分几何发展史上扮演着重要角色，成为21世纪数学研究的主攻方向，目前已在数理统计、控制论和多端信息理论等领域有着广泛的应用[1-2]。设M 是一个n 维的光滑流形，TxM 表 示x ∈M 处 的 切 空 间，其 切 丛上的非负函数F:，称为Finsler度量，如果F满足：(i)光滑性，在切丛TM{0}上F(x,y)是光滑函数；(ii)正齐性，正则性，矩阵在切丛上是正定的，其中张量g=gij(x,y)是切丛TM 上的二阶对称且正定的共变张量，称为F 的基本张量。称具有Finsler度量的流形为Finsler流形，记作(M,F)。

存在大量非Riemann 的Finsler 度量：(i)根据F 的正齐性，光滑流形上的Riemann 度量gij(x)=可以构造两个Finsler度量

下面给出球对称Finsler度量和对偶平坦的Finsler度量的相关概念以及满足对偶平坦的特殊属性。

Amzri等在Riemann流行上研究信息几何学时提出了对偶平坦的概念。文献[4]研究了在去掉二次型限制的条件下，将对偶平坦这个概念推广到Finsler流形上，并证明了在开域上的Finsler度量F =F(x,y)是对偶平坦的当且仅当F 满足偏微分方程在文献[5]中研究了开集上的球对称Finsler度量F=F(x,y)是对偶平坦的充要条件，即开集上的球对称Finsler度量

是对偶平坦当且仅当f满足偏微分方程

研究和构造对偶平坦并具有非零数量旗曲率的Finsler度量是Finsler几何中的一个经典问题。文献[6]中给出非Riemann的对偶平坦Finsler度量这是定义在单位球上的Funk度量，其中 |· |和＜, ＞分别表示为标准的欧几里得范数和内积。

文献[7]通过射影平坦的Finsler度量利用射影因子构造了一些对偶平坦的Finsler度量。文献[8-9]也给出了对偶平坦的球对称Finsler度量的若干例子。本文通过解球对称Finsler度量成为对偶平坦度量所满足的一个偏微分方程（2），构造两类不同形式的f (t,s)，即f (t,s)=(s)和f (t,s)=通过分离变量及Maple运算得到两类具有一般形式的对偶平坦的Finsler度量。

定理1若f (t,s)定义为其中λ,c1,c2均为任意常数，则球对称Finsler度量在单位球Bn(1)上是对偶平坦的。

证明通过分离变量法给出方程（2）的一个解，设f (t,s)=φ(t)+ψ(s)是方程（2）的解，则有

其中c1,为任意常数。

定理2若f (t,s)定义如下：

其中λ,c1,c2,c3,c4均为任意常数，且λ ＞是关于x 的误差函数，则球对称Finsler度量在单位球Bn(1)上是对偶平坦的。

证明通过分离变量法给出方程（2）的另一个解，设f (t,s)是方程（2）的解，则有

方程（6）的通解可表示为

其中λ,c1,c2为任意常数，且λ ＞0,c1≠0。通过Maple运算，可得方程（7）的通解为

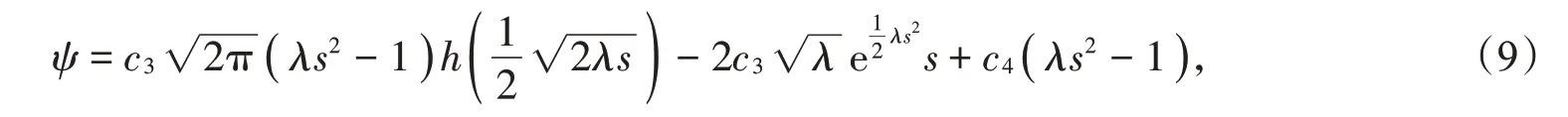
其中c3,c4均为任意常数。联立（8）式和（9）式，得到方程（2）一个通解为

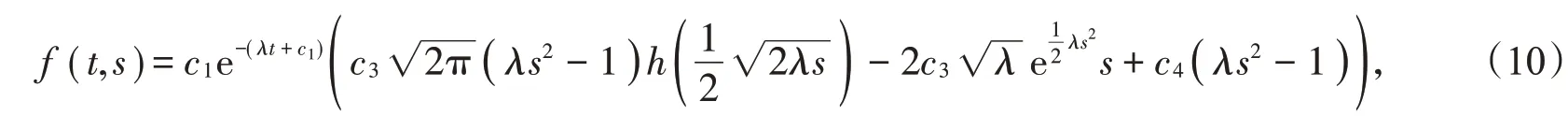
其中λ,c1,c2,c3,c4为任意常数，由（1）式和（10）式可得定理2得证。

本文利用球对称Finler 度量成为对偶平坦度量满足的一个偏微分方程，先构造了两类一般形式的f (t,s)，并运用较强的技巧计算出f (t,s)的具体表达式，进而得到两类球对称的对偶平坦Finler度量，为球对称Finler度量的研究提供了一种方法。