一种基于梯度下降四元数理论的DVL误差标定方法

徐晓苏，杨 阳，李 瑶

（1.微惯性仪表与先进导航技术教育部重点实验室，南京 210096； 2.东南大学 仪器科学与工程学院，南京 210096）

水下自主航行器（AUV）无论在军用还是民用领域都有着广泛的应用前景，导航定位一直是AUV 的一项关键技术。单一的惯性导航系统（INS）具有强自主性、强隐蔽性等优点，是AUV 的理想导航方式，但其系统误差会随时间累积，长时间工作会导致其导航精度下降而无法满足精度要求。SINS/DVL 组合导航系统利用DVL 速度信息对SINS 导航误差进行估计并补偿，获得较高的导航精度。因此，SINS/DVL 组合导航系统常被用于AUV[1]。

多普勒测速误差是影响SINS/DVL 组合导航系统精度的重要因素，其误差来源包括比例因子误差、安装偏角误差、载体姿态误差、波束宽度误差、洋流速度[2]等等，其中比例因子误差和安装角偏误差的标定研究对提高SINS/DVL 组合导航定位精度有着重要意义[3]。因此，关于这两种误差标定技术是SINS/DVL水下组合导航领域的研究热点之一。

对于比例因子误差和安装误差角的标定方式，常用的包括在线自标定和预标定等。在线自标定即把测速误差参数作为卡尔曼滤波器的状态进行在线估计，是解决问题的一个思路。但是，AUV 通常采用匀速直 航的航行方式，在该航行方式下，测速误差参数的可观测度比较弱，而且由于在标定过程中直接采用了DVL 的量测输出，引入了DVL 量测噪声，使得标定曲线呈现噪声特性，难以取得比较好的估计效果[4]。

本文针对以上问题，采用预标定的方法，以SINS/ DVL/GNSS 作为组合导航方式，提出了一种基于梯度下降四元数估计理论的位置观测标定方法。由于该方法是基于位置矢量的标定，通过利用四元数梯度下降法，构造位置矢量观测器方程，避免了DVL 量测噪声对标定结果的影响，可进一步提高标定精度。试验结果表明，与直接利用DVL 量测速度标定的算法相比，基于位置观测法的标定曲线更加平滑，精度更高。

1 DVL 主要误差分析

1.1 比例因子误差

在实际应用的DVL 测速系统声速计算公式中，一般将声波在水中的传播速度c0视为常值，即1500 m/s。但是声波在水中的实际传播速度受水的温度、盐度和水压等因素的影响，用常值来代替一个实际变化的量必然会带来计算误差。其中，温度和盐度对声速的影响最大：水温每变化1℃，声速变化所引起的测速误差达到0.2%；海水盐度每增加0.1%，声速变化所引起的测速误差为0.07%[5]。此类误差的作用在DVL 比例因子的数值变化上呈现。

1.2 安装误差角

在SINS/DVL 组合导航系统中，安装误差角是指DVL 与惯导测量单元IMU 之间的安装姿态关系[6]。对于SINS/DVL 组合系统，当进行速度匹配时，SINS 和DVL 的速度信息必须基于同一坐标体系，但是当SINS和DVL 的测量坐标系存在误差时，即DVL 存在安装误差时，必然会影响组合导航的精度。在工程实践中，仪器设备都存在误差，安装偏角误差无法避免，会造成DVL 和IMU 对速度信息测量不一致[7]。因此，需要明确两者的安装偏角关系。如图1所示，可以更直 观了解两者的安装偏角关系[8]，其中，x B-y B-zB指载体坐标系（b系），x D-y D-zD指DVL 坐标系（d系）。

图1 安装误差角示意图 Fig.1 Schematic of installation error angle

2 位置观测标定算法原理

算法原理框图如图2所示。AUV 在水面航行时，利用SINS/GNSS 组合导航系统，得到载体的姿态、速度和位置信息，再根据DVL 测量得到的速度信息，按照提出的标定算法进行误差标定。

图2 标定原理框图 Fig.2 Block diagram of calibration principle

2.1 比例因子误差的标定

根据DVL 的测速原理，其输出为：

式中，表示DVL 输出速度；ς表示比例因子误差；表示b系到d系的姿态转换矩阵；Cnb表示n系到b系的姿态转换阵；vn表示载体在导航坐标系（东北天坐标系n系）中的运动速度；表示b系相对于n系的旋转角速度在b系上的投影；表示DVL 与SINS 之间的杆臂距离在b系上的投影；ηd为DVL 的量测误差。

根据DVL 测速原理可知，当进行SINS/GNSS 组合导航时，有如下关系式：

式中，表示DVL 输出速度；Cbd表示b系到d系的姿态转换矩阵，一般为常量；ς表示比例因子误差；表示SINS/GNSS 组合之后的姿态变换阵；表示SINS/GNSS 组合速度在n系下的值；表示b系相对于n系的旋转角速度在b系上的投影；表示DVL 与SINS 之间的杆臂距离在b系上的投影。

可由下式计算：

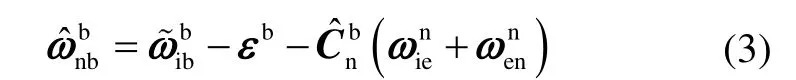
式中，表示陀螺输出量εb为陀螺漂移，为n系相对惯性空间角速度在n系下的投影。由于GNSS信号有效，则载体的姿态、速度和位置信息等都可以准确获得，因此可以通过计算得到。

由于姿态转换矩阵不会改变向量的模值，而且相对AUV 的运动角速度，陀螺零偏εb为小量，其对应的杆臂速度可以忽略，对式(2)进行取模运算得到：

计算得到利用速度观测算法的DVL 比例因子误差为：

由于式(5)得到的DVL 比例因子误差直接利用了DVL 的速度引入了量测噪声，所以对式(2)左右两边进行位置运算，式(2)左边为：

式中，下标k表示离散时刻，ΔtD表示DVL 采样时间间隔。

若在每次多普勒测速仪的采样间隔内，SINS/GNSS 解算得出N个数据，则对SINS/GNSS 位置离散化计算得到式(2)右边为：

所以，得到基于位置观测标定算法的比例因子误差为：

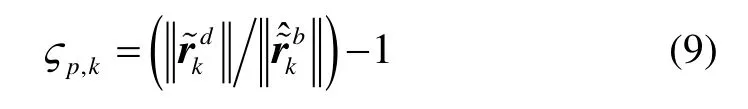
2.2 安装误差角的标定

将上述利用速度观测方法标定出来的结果式(5)代入式(2)有：

为了实现安装角快速、准确标定，本文参考梯度下降四元数姿态估计器[9-10]，提出了一种基于梯度下降四元数估计理论的安装角确定算法。根据上述得到的公式，令：

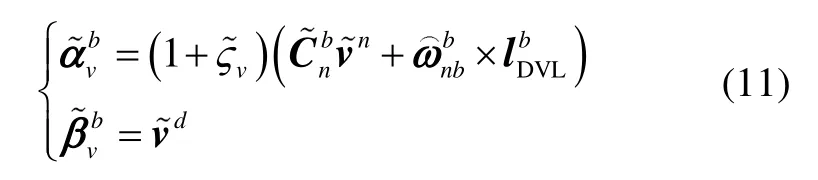
构造速度观测器矢量方程：

同样，为了实现安装误差角的标定不受DVL 量测噪声的影响，利用基于位置观测标定算法计算得到的比例因子误差，由式(9)得：

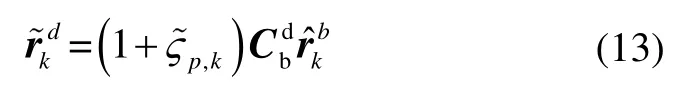
根据梯度下降四元数的估计理论算法，构造目标函数：

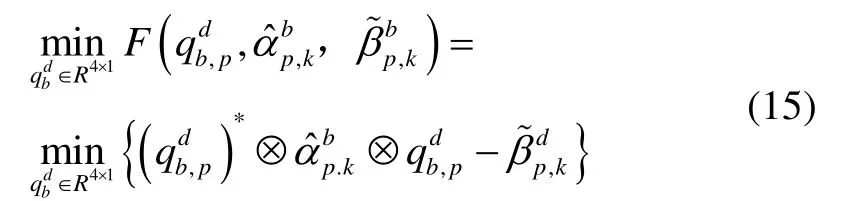
其中，表示由b系到d系的转换四元数，表 示该四元数的共轭四元数。

基于式(15)的最小化，根据文献[9][10]得到基于算 法的最优姿态四元数确定的迭代方法：

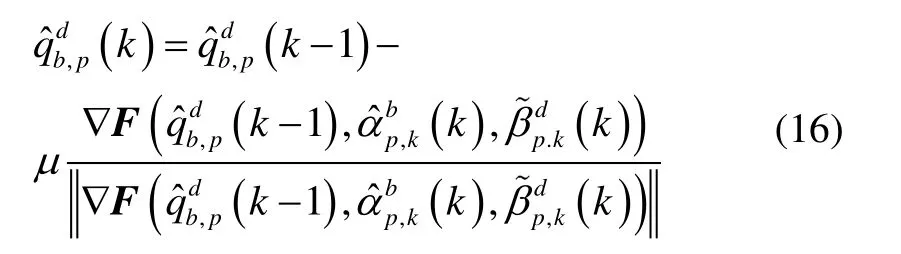
式(17)中JT表示函数F关于变量qbd的雅可比矩阵函数的转置形式。由式(15)和式(17)可知F和J的表达式：

式中，F是的简单表示形式，J是的简单表示。由式(16)可知，需 要求解权值系数μ。为了实现更精确的误差标定，本文将该系数看作为一个变化量，构造式(19)表示的梯 度四元数，通过迭代计算，实现该系数的最优化。

根据式(19)，选取合适的μk，可以保证收敛。当迭代步长较大时会带来一定的扰动，因此μk应满足下列的约束条件：

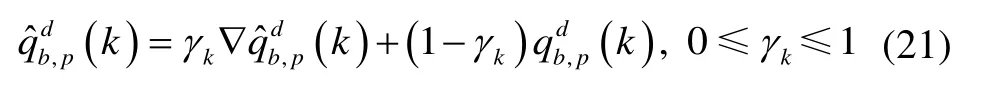
式中，γk表示互补滤波权值。为权衡引入选取准则其中σ表示的递推发散速率，μkΔtD表示梯度控制收敛速率。将解得的γk表达式与式(13)代入式(21)，考虑到DVL 和SINS 固联为零向量，并且μk远大于σ，整理得到以下算法迭代格式：

利用式(22)，选取合适的发散系数σ，即可得到基于位置观测法的安装角对应的四元数，从而实现对安装角的标定。

至此，基于位置观测法的比例因子误差和安装角均得到标定。

根据式(11)(12)采用同样的方法可以得到基于速度观测方法的安装误差角的标定结果，在仿真验证及半物理试验部分与基于位置观测法的结果做了对比。

3 仿真验证

本文提出了基于位置观测的DVL 比例因子误差以及安装角的标定方法，并将基于速度观测的标定方法也做了仿真及试验验证，与文献[6]提出的卡尔曼滤波标定方法进行对比。其中，位置观测标定法命名为GD-p，速度观测标定法命名为GD-v，文献[6]提出的方法命名为CKFM。

为了提高卡尔曼滤波标定算法中DVL 比例因子误差和安装误差角的可观测度，仿真轨迹选取S 型。

仿真过程中，仿真时间为600 s，在每次方位转弯时，AUV 都先以0.5 (°)/s 的角速度横滚4 s，以横滚出转弯协调角，当方位转弯完成后，又以0.5 (°)/s 的角速度反向横滚4 s，轨迹如图3所示。系统工作的初始位置为东经118.786°，北纬32.057°；惯性传感器的参数设置为陀螺仪常值漂移0.02 (°)/h，随机游走0.02 (°)/h；加速度计常值偏置500 μg，随机偏置50 μg；IMU 数据输出频率200 Hz，捷联结算周期5 ms；GNSS 数据输出频率1 Hz；DVL 的测速精度0.5%v±0.5cm/s，比例因子误差设置为0.005；数据输出频率为1 Hz；DVL与SINS 之间的杆臂长度设置DVL 与SINS 之间的安装角设置为φθ=1°，φγ=0.8°，φΨ=0.6°；SINS/ GNSS 组合导航系统的初始姿态误差设置为 [0.5° 0.5° 1° ]T；速度误差均设置为0.1 m/s，位置误差为5 m。其中，图4为3 种方法下的比例因子估计值误差对比图，δk表示比例因子估计值误差。图4～6 为3 种方法下的安装角估计误差的对比图，δφ θ、δφ γ、δφ Ψ分别表示x轴安装角估计误差、y轴安装角估计误差和z轴安装角估计误差。

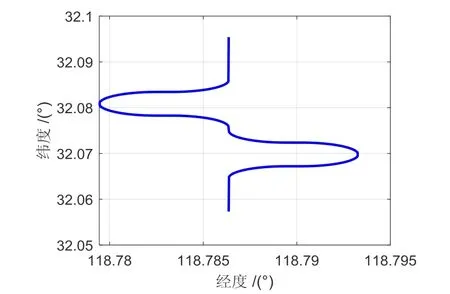
图3 仿真轨迹 Fig.3 Simulation trajectory

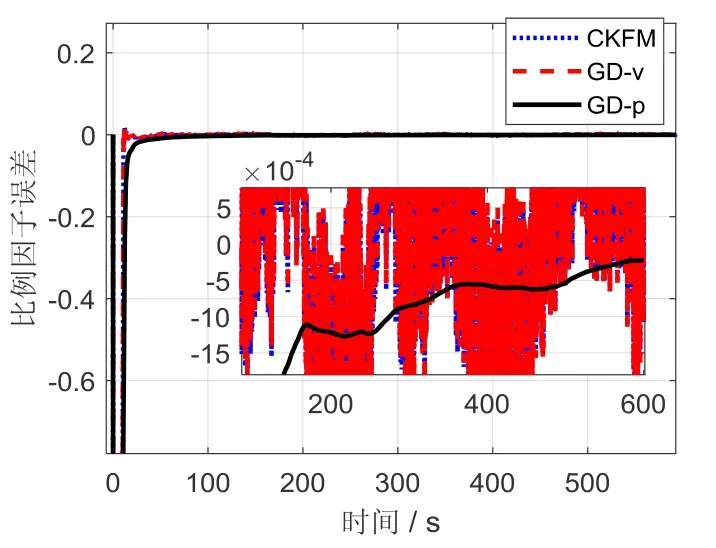
图4 比例因子估计值误差 Fig.4 Scale factor estimation errors

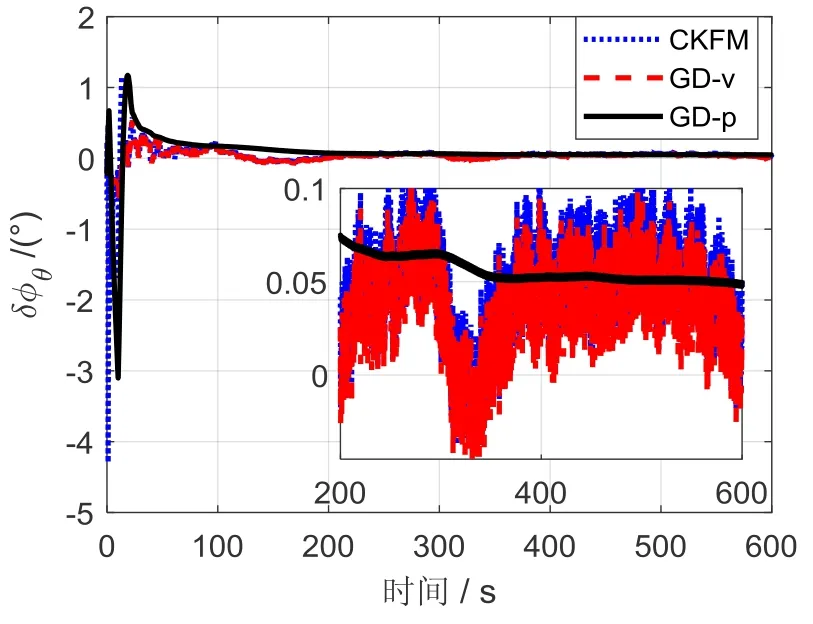
图5 x 轴安装角估计误差 Fig.5 x-axis mounting angle estimation error

图6 y 轴安装角估计误差 Fig.6 y-axis mounting angle estimation error

图7 z 轴安装角估计误差 Fig.7 z-axis mounting angle estimation error

图4下面部分是局部放大图，可以看出，由于是直接利用DVL 量测速度进行的标定，因此基于速度观测法和卡尔曼滤波标定法的结果是呈现噪声特性的。而采用GD-p 方法后，可以有效避免这种影响，最终比例因子估计值误差在0.06%以内，精度有很大提高。采用位置观测法以后，有效抑制了标定结果的 噪声特性。图5表明，CKFM 和GD-v 方法标定的x轴安装角估计误差在0.1°左右，而采用GD-p 方法，标定结果可达到0.05°左右，精度有所提高。图6表明，y轴安装角估计误差没有得到标定。由于载体一直以y轴方向为前进轴，垂向速度和横向速度均为小量，由文献[7]可知，y轴安装误差角不会影响SINS/DVL 组合定位精度,因此可忽略其误差的影响。图7表明，CKFM 和GD-v 方法标定的z轴安装角估计误差在0.15°左右，而采用GD-p 方法，标定结果可达到0.03°左右，精度大幅度提高。

4 半物理试验验证

为了进一步验证本文提出的标定方法的可行性和有效性，采用实验室2017年12月5日车载数据进行半物理仿真验证。在本次车载试验中，姿态、速度、位置等导航参数的真值由法国IXBLUE 公司研制的PHINS 和NovAtel 公司研制的FlexPark6 接收机进行SINS/GNSS 松组合来提供。DVL 速度由PHINS 和GNSS 松组合下的速度来模拟，与捷联惯导系统的输出进行SINS/DVL 组合，该系统信息融合周期为1 s。在车载试验前，捷联系统经过了实验室标定过程，补偿了惯性器件的部分常值误差。捷联系统的陀螺常值漂移为0.01 (°)/h，随机游走为0.01 (°)/h1/2，加速度计零偏为50 μg，DVL 系统更新频率设置为1 Hz，与惯导系统的安装角设置为φθ= 1° ，φγ= 0.8° ，φΨ= 0.6°，比例因子估计值误差设置为0.005。跑车图以及安装实物图如图8所示，图中上侧红色圈注地方为GNSS 天线。

图8 样机跑车和安装实物图 Fig.8 Prototype car and installation physical

本次车载试验持续3700 s，0～1540 s 期间进行初始对准，为后期的组合姿态提供高精度的导航信息。本次验证试验选取对准结束后的600 s 数据进行算法验证，图9为车载试验轨迹，图10～13 为根据本文提 出的算法进行的标定对比曲线。

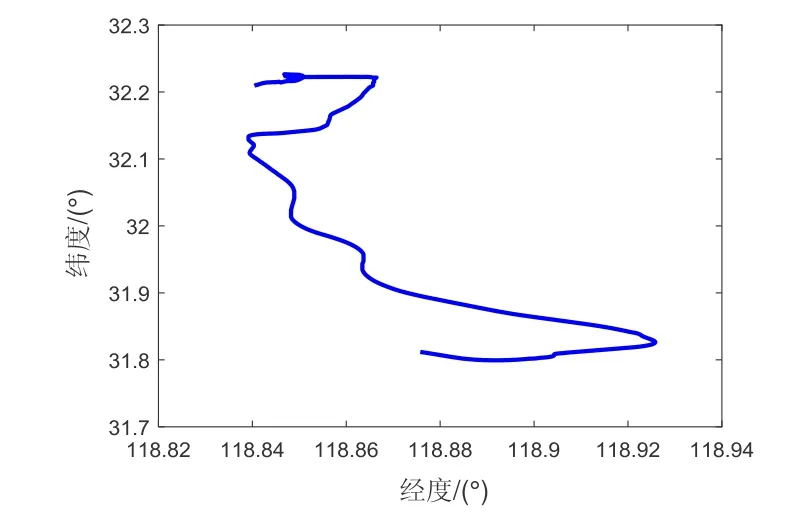
图9 车载试验轨迹 Fig.9 Prototype car trajectory

图10 比例因子估计值误差对比 Fig.10 Comparison on scale factor estimation errors

图11 x 轴安装角估计误差 Fig.11 Estimation error of x-axis mounting angle

图12 z 轴安装角估计误差 Fig.12 Estimation error of z-axis mounting angle

从图10～12 可以看出，当采用卡尔曼滤波在线标 定和速度观测法时，由于直接采用了量测速度进行标定，曲线受到量测噪声的影响较大。采用基于位置观测的标定方法后，精度有很大提高。图10 表明，比例因子估计值误差在5×10-4以内；图11 和图12 表明，对安装角估计值误差的标定，相比于采用卡尔曼在线标定和基于速度观测法标定，均保持在0.02°以内。

表1表示的是3 种方法下比例因子估计值误差、x轴安装角估计误差和z轴安装角估计误差的均方根误差的统计值。从表中可以看出，由于基于位置观测法对DVL 输出速度进行了积分处理，有效降低了量测噪声的影响，使得该方法标定结果的均方根误差明显小于其他两种方法。

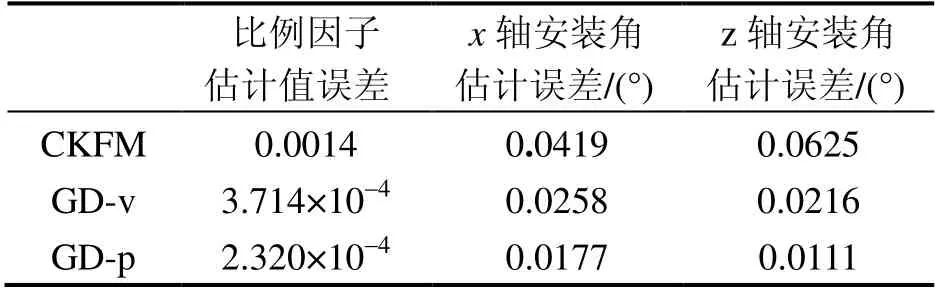
表1 估计误差均方根误差 Tab.1 Estimation error root mean square error

5 结 论

本文为了提高SINS/DVL 水下组合导航的定位精度，提出了一种基于梯度下降四元数估计理论的位置观测DVL 标定方法，在GNSS 信号辅助下，利用多普勒测速原理标定出比例因子估计值误差，通过构造位置矢量观测方程，采用梯度下降四元数方法得到安装角估计误差的标定结果，并将这种方法与卡尔曼滤波在线估计和基于速度观测法做了对比。仿真及试验结果表明，位置观测法可以更精确、更快速的标定出DVL 的比例因子值和安装角估计值。