基于EMD-PSO-LSTM组合模型的船舶运动姿态预测
2019-11-20彭秀艳
彭秀艳,张 彪
(哈尔滨工程大学 自动化学院,哈尔滨 150001)
由于在海上航行过程中,船舶不可避免地会受到风浪和洋流等外部因素的影响,从而导致船舶出现横荡、纵荡、艏摇、横摇、纵摇和升沉等难以控制的复杂运动。由于船舶在作业方面存在特殊性,当其常态化运动模式被打破,将可能造成无法预料的后果。尤其是当海域状况恶劣时,船舶摇摆不定的状态,将导致作业活动的开展存在不安定因素。因此提高对船舶摇荡姿态的预报性能,能够确保当船舶在大风浪中作业时有效提高活动的安全性。比如提升船舶行进、锚泊、动力定位等活动的安全系数,避免因转向时机选择失误导致引发翻沉、走锚等事故。此外,提高对船舶摇荡姿态的预报性能还能够有效强化海军舰载武器、装备等设备的使用效能。由此可知,船舶运动姿态的短期预测研究意义是十分重大且深远的。
在船舶运动姿态预测方面现有的预测算法主要有卡尔曼滤波法[1-2]、谱估计法[3]、艏前波法(惯性)[4]、基于自回归模型的方法[5]、基于混沌分析的方法[6]和人工神经网络方法[7-9]等。其中时间序列方法一般适用于短期预测,当存在外界干扰时,预测偏差较大;而传统的灰色预测法具备运算简便,信息量要求低等优点,但该方法的不足之处在于不适于波动剧烈的序列,无法满足高精度运用场景的需要,同时当样本较大时也不适用。然而神经网络方法的适应性和学习能力均比较突出,在非线性研究工作中具有显著的普适性。
当前常用的预测方法往往运用单一的预测模型完成时间序列建模工作,当面对复杂多变、呈现数多变量动态演化行为的非线性时间序列时,其无法直观体现出相应序列的非线性,因此相应的预测结果的准确性也有所欠缺。然而组合预测模型[10-11]有效解决了上述问题,在充分发挥每个单一预测模型优势的基础上,实现整体预测结果的准确性。所以,当时间序列具备显著随机性和特征信息丰富的特点时,应当采用逐一应对的思想,探究出建立于经验模态分解[12](Empirical Mode Decomposition,EMD)之上的预测方式,通过将无规律性的船舶运动姿态时间序列问题转化为若干个规律性显著的分量预测问题,随后将分量预测的结果进行合并分析最终得到精度较高的预测值,进而促使建模更加简易,结果精度更高。
正是在上述思想的指导下,本文提出基于经验模态分解和粒子群优化的LSTM 神经网络(PSO-LSTM)组合的船舶运动姿态预测模型。该模型包括基于EMD的船舶运动数据分解与PSO-LSTM 神经网络的分量预测和结果叠加三个部分。将EMD-PSO-LSTM 模型与LSTM 模型、PSO-LSTM 模型三者的结果进行对比探究,研究证实该方法的优势较为显著,在有效降低建模难度的同时明显提升了预测结果的精度和效率。
1 经验模态分解
作为处理非线性、非平稳时变序列的有效方法,经验模态分解(EMD)能够依据数据本身的时间尺度特征自适应分解信号,被公认为是建立在平稳和线性假设基础上的小波和傅里叶两种分析模式的突破。该算法的数据分析过程能够实现将复杂化的时序数据分解成为有限个本征模函数(Intrinsic Mode Function,IMF),而分解获得的IMF分量具备原数据在相应时间尺度上的所有波动信息。
设定原始时序样本数据为x(t),首先运算得出该数据上的局部最大值和最小值,随后根据所得数值进行插值拟合运算,求得x(t)的上下包络xmax(t)和xmin(t)序列,最后求上下包络序列的均值,从而获得均值序列m1(t):

用原始序列减去均值序列得到去掉低频的新序列h11(t):
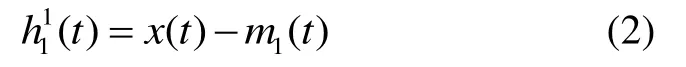
通常情况下,当h11(t)不符合征模函数的有关条件是,应将其视为原始序列,随后进行重复运算,重复k次直到平均曲线趋近于零后方可停止。记c1(t) =h1k(t),同时将c1(t)视作IMF 的判断条件为:

式(3)中SD作为筛分门限,通常当其取值维持在0.2~0.3 之间比较合理。在x(t)中减去c1(t),可得到剔除最高频成分的残差序列r1(t) =x(t) -c1(t)。IMF分量的获取可通过重复上述的筛选过程实现,当预定误差大于cn(t)或者rn(t)为单调函数时,方可停止模态分解过程。而相应的原始序列可通过n阶IMF分量和残差rn(t)表示如下:
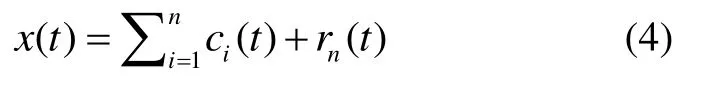
2 基于粒子群优化的LSTM 神经网络算法
2.1 粒子群优化算法
粒子群优化算法[13(]PSO)是1995年,由Kennedy、Eberhar 所提出的算法,该算法是一种通过模拟鸟群觅食行为的群智能优化算法,族群中所有粒子都对应停留在设定的搜索空间中,如式(5)(6)所示:两个公式通过不断地调整自身的速度和位置进行寻优,直到满足收敛终止条件。

式中:为第t次迭代时第j维中粒子i的速度;为i对应的位置;ω表示惯性权重;c1、c2表示加速度系数(学习因子);粒子群第t次迭代时的个体极值点;为粒子群的全局极值点;为[0,1]区间内均匀分布的随机数;是常数。
2.2 LSTM 神经网络
长短期记忆[14](LSTM)神经网络作为比较特殊的循环神经网络,其能够对依赖信息进行长时间学习,并且有效规避梯度消失现象的出现。此外其能够将记 忆单元(Memory Cell)根植于循环神经网络隐藏层的神经节点之中,实现对历史信息的记录,并且通过增加(Input,Forget,Output)三种门结构可实现对历史信息的运用。

式中:it、ft、ot依次表示input、forget、output 三类门结构;ht-1是前一时刻隐藏层单元的输出信息,h t代表当前输出信息;cell 单元则用ct表示;W h、Wx、W c分别代表不同连接层的权重矩阵;sigmoid 与tanh 为两种激活函数。

图1 长短期记忆神经网络单元结构图 Fig.1 Structure of long- and short-term memory neural network cell
2.3 PSO-LSTM 算法
该算法的主要思想是通过PSO算法优化LSTM网络的权值,这样能够改善LSTM 网络的预测性能。
具体步骤如下:
步骤1:初始化粒子群参数及LSTM 网络的结构。粒子群参数包括种群规模、层数,迭代次数、学习因子、粒子位置和速度取值的限定范围,在这之中随机值为粒子速度和位置的初值。LSTM 网络结构的初始化主要是指网络各层神经元个数及隐含层层数的确定。
步骤2:确定粒子的评价函数。种群中粒子的适应度函数定义为:
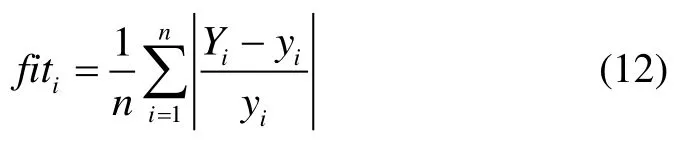
式中,n表示种群规模,Yi为样本输出值,yi为实际输出值。
步骤3:计算每个粒子的适应度值,构建种群规 则树结构。根据公式(12)计算每个粒子的适应度值并进行排序,然后构建粒子群种群规则树结构。
步骤4:实时更新粒子局部和全局的最优位置。
步骤5:依据式(6)更新粒子本身的速度和位置。
步骤6:如果达到迭代结束条件(最大的迭代次 数),则结束,否则转步骤3 继续迭代。
步骤7:将得到的最优结果对LSTM 网络的连 接权值进行赋值,LSTM 网络预测模型经训练后,输出时间序列预测最优解。
PSO-LSTM 算法的流程图如图2所示。

图2 PSO-LSTM 算法流程图 Fig.2 Flow chart of PSO-LSTM algorithm
3 基于EMD-PSO-LSTM 的组合预测模型
由于船舶运动姿态时间序列普遍存在的复杂特性,假如在预测阶段涵盖所有特性的分析,毫无疑问将会大幅提升模型构建的难度,同时造成模型性能的陡降。EMD 方法作为结合信号自身的特性完成自适应分解,无需事先设定基函数,有效避免出现因科研人员主观经验造成的误差情况。PSO 优化算法作为群体智能算法,属于启发式优化算法,并且该算法也属于进化算法的一种,能够科学处理无约束和约束全局的优化问题。LSTM 神经网络由于自身内部结构的特点,能够实现对依赖信息的长时间学习,并且有效规避梯度消失现象的出现。本文综合借助上述两种算法优势的发挥,并将两者与EMD 算法结合起来进行船舶运动姿态的预测,提出了一种新型的船舶运动姿态组合预测模型EMD-PSO-LSTM 模型。
基于EMD-PSO-LSTM 组合预测的船模运动姿态预测步骤如下:
步骤1:船舶运动姿态序列分解。运用EMD 分解程序,将其分解为n组频率不同的样本模态分量和残差项rn。
步骤2:本征模态分量的PSO-LSTM 时序预测。依据频率不同的IMF 分量和残差项rn对应构建PSO-LSTM 模型,完成时序预测任务并对相应结果进行求和。
步骤3:预测结果计算。
EMD-PSO-LSTM 组合模型预测流程如图3所示。

图3 EMD-PSO-LSTM 组合模型的船舶运动姿态预测流程图 Fig.3 Flow chart of ship motion attitude prediction based on EMD-PSO-LSTM integrated model
4 仿真结果与分析
4.1 仿真条件设置
在仿真过程中,本文采用某船舶在四级海况下,航行速度为20 kn、遭遇角为135°时的船舶运动姿态的实测的升沉位移数据、纵摇角数据和横摇角数据来分别进行仿真,每类数据总计1000 个,采样时间为0.05 s,其中训练样本与预测样本的数量分别设置为800、200,PSO 的参数按照表1中所示进行设置。

表1 PSO 参数设置 Tab.1 Parameters of PSO algorithm
4.2 EMD 分解
以升沉位移为例,将船舶升沉数据按照EMD 流程分解,获得具有不同波动尺度信息的本征模态分量,其中得到5 个基本模式分量IMF1~IMF5和一个剩余分量Res。IMF1的频率较高,代表升沉信号中的高频成分;而Res 是低频信号,代表信号中含有的非线性趋势项。图4为升沉位移时序曲线及进行分解后的各模式分量。

图4 升沉位移时序曲线及其EMD 分解 Fig.4 Sequential curve of heave displacement and its EMD decomposition
4.3 仿真结果与分析
在仿真之前,为了加快训练速度,需要采用式(13)对数据进行归一化处理,将其归一化到[0,1]。

其中,xi是输入的数据 (i=1,2,) ,xmax是数据中的最大值,xmin是数据中的最小值,Mi是归一化后的数据。
当前关于预测误差的评价指标有很多,本文主要采用MAPE(平均绝对百分比误差,Mean Absolute Percentage Errors)和RMSE(均方根误差,Root Mean Square Error)作为预测结果的评价指标,计算公式如下:

为了更好地说明EMD-PSO-LSTM 模型在船舶运动姿态预测中的优越性,本文同时利用LSTM 模型及PSO-LSTM 模型对船舶运动姿态数据进行预测,其中三个模型中LSTM 的输入层节点数均设置为1,隐含层节点数设置为4,隐含层层数设置为3,输出层节点数设置为1,初始学习率设置为0.001,采用tanh 和sigmoid 函数作为激活函数。LSTM 的权值及网络结构参数主要利用网格搜索来进行选取。图5为三种模型的预测结果对比图,图6为三种模型的预测误差对比结果图,表2~4 为三种模型预测结果的MAPE 和RMSE 的对比结果。
通过分析图5~6 及表2~4 可以看出,EMD-PSO- LSTM 组合模型相对于LSTM 模型和PSO-LSTM 模型:在对升沉位移的预测中,预测结果的平均绝对百分比误差上分别降低了10.68%、7.71%,均方根误差(RMSE)分别降低了0.0515 m 和0.0306 m;在横摇角的预测中MAPE 分别降低了11.09%和7.84%,RMSE 分别降低了0.1584°和0.0922°;在纵摇角的预测中MAPE 分别降低了10.97%和6.54%,RMSE 分别降低了0.0444°和0.0213°。分析结果表明EMD-PSO- LSTM 模型是一种更为有效的船舶运动姿态预测方法。

表2 升沉位移误差统计结果 Tab.2 Statistical results of heave displacement errors

表3 横摇角误差统计结果 Tab.3 Statistical results of roll angle errors


图5 三种模型预测结果 Fig.5 Prediction results of the three models


图6 三种模型预测误差 Fig.6 Prediction errors of the three models

表4 纵摇角误差统计结果 Tab.4 Statistical results of pitch angle errors
三种模型的预测结果与实际值的变化曲线基本一致,能够反映出数据的变化规律。相对于另外两种模型,EMD-PSO-LSTM 组合模型的预测结果在均方根误差及平均绝对百分比误差上均为最小,说明其预测精度总体上要比其它两种模型高,对于具有非平稳、非线性特征的船舶运动姿态具有更好的预测效果。
5 结 论
本文针对船舶运动姿态的高随机性和复杂性特征,建立了基于EMD-PSO-LSTM 的船舶运动姿态预测模型。该模型首先将船舶运动姿态数据用EMD 算法进行分解,然后利用PSO-LSTM 模型对各分量进行预测,最后将预测值代数相加得到最终的预测结果。在实验中,本文将EMD-PSO-LSTM 与LSTM 模型、PSO-LSTM 模型分别对某船舶在四级海况的船舶运动姿态数据进行预测对比,结果表明:EMD-PSO-LSTM模型在提高船舶运动姿态预测的整体精度的同时将绝大部分预测点与实际数据的偏离程度控制在较小范围,从而促使预测的准确性得到提高。这主要是因为该模型将复杂的船舶运动姿态预测问题转化为若干个规律性显著的分量预测问题,随后在预测结果合并运算的基础上求得精确度较高的预测值,提高了预测精度。
在当前的船舶运行姿态预测中,利用LSTM 等深度学习模型的相关方法较少。在后续的研究中,一方面将重点研究LSTM、GRU 神经网络等深度学习模型在船舶运动姿态预测的应用,另一方面,将重点研究LSTM 等深度学习模型与GA 等群体智能算法的结合,进一步增强LSTM 等深度学习模型在实际应用过程中的效果。
