集群无人机定位信号的自适应GM-CBMeMBer滤波算法

黄 鹤，郭 璐，许 哲，王会峰，孟 芸，代 亮

（1.长安大学 电子与控制工程学院，西安 710064；2.西安爱生技术集团公司，西安 710075； 3.无人机系统国家工程研究中心 西北工业大学，西安 710072；4.中电科第20 研究所，西安 710068）

现有的无人机在执行任务时，需要通过地面站进行一对一的控制才能完成其使命。随着任务复杂度的提高，利用无人机集群实施大规模密集作业的需求日益迫切。集群的主要关键技术包括大规模无人机管理与控制、多无人机自主编队飞行、集群感知与态势共享、集群突防与攻击、集群任务控制站等，自组织协同通信系统是无人机集群的核心，可以交互导航定位信号和控制指令。在实际执行任务中，由于空间杂波信号、气候变化等因素会给无人机集群自组织协同通信系统带来大量干扰，严重影响无人机导航定位性能。尤其在多目标定位的场景下，会涉及到两个问题：1）每个目标的出现和消失都是一个随机过程，因此，目标的数量是随时间变化的；2）在噪声影响和目标密集分布的情况下，测量数据的关联难以实现，直接影响信号检测的精度。近年针对以上问题的研究产生了众多信号处理算法，其中包括基于数据关联的多目标预测算法，即MTT（Multi-target Tracking）算法[1]。由于数据关联造成内部耦合，随着目标数目的增加，可能会出现组合爆炸而导致数据量过大等情况。Malher通过引入有限集FISST（Finite Set Statistics）理论，提出了基于随机集RFS（Random Finite Set）的多目标跟踪理论[2]，并在此基础上提出了概率假设密度滤波算法（Probabi- lity Hypothesis Density,PHD）[3]和势概率假设密度滤波方法（ Cardinality Probability Hypothesis Density,CPHD）[4]。然而，该算法实现条件过于理想，通常需要假设新生目标从事先设置的固定位置开始执行跟踪，同时不能提供航迹信息。如果新生目标出现在未覆盖的目标出生强度范围内，则概率假设密度PHD 和CPHD 无法引领航迹，会增加虚假短小航迹的概率。高斯混合PHD（Gaussian Mixture PHD,GM-PHD）[5-6]和高斯混合 CPHD（Gaussian Mixture CPHD,GM- CPHD）[7-8]使用多个高斯分量来逼近目标出生强度，但要求精度更高的平均值、权重和协方差，不合理的参数设置还会影响航迹初始状态的性能效果。2008年，Mahler 提出了基于多伯努利随机集的多目标多伯努利（MeMBer）滤波算法[9]，在滤波过程中递归估计多伯努利随机集的参数，可以更加直观地解决多目标估计问题。针对高估目标数量的问题，Vo 提出了基于多目标平衡的多目标多伯努利滤波器（CBMeMBer）[10]，解决了经典MeMBer 滤波器过估目标的问题，在此基础上提出了基于高斯混合的CBMeMBer（GM-CBMeMBer）滤波算法[11]，但是随机噪声干扰会导致内部滤波器存在发散的问题。

为了解决随机噪声带来的滤波器发散问题，实现对集群无人机定位信号的滤波和预测，本文在高斯混合的CBMeMBer 滤波算法的基础上引入了高斯项的剪枝合并分别构建了多目标模型、状态和测量模型、新生目标模型三种模型。此外，在对高斯密度函数协方差预测时，由于实际噪声统计特性的不确定性，传统算法的预测会导致更新结果不能及时准确地反映实际状态，而本文算法中加入衰减因子来预测高斯密度函数协方差，确保预测值为当前噪声干扰下的实时估计值，实现更新值真实性和实时性。

1 多目标定位信号滤波模型

1）多目标模型

在构建的多目标模型中，其检测空间为[-1000 m,1000 m]×[-1000 m,1000 m]的水平区域，检测时间长度为100 s，处理12 架无人机机动目标的定位问题。

多目标信号数学模型由两部分组成，可以准确的描绘信号的运动特征，并易于处理：一部分表示信号在x和y方向上的初始位置和运动状态；另一部分表示信号所持续的时间。

2）状态和测量模型

线性高斯随机状态空间中的状态模型和观测模型分别描述为：

3）新生目标模型

2 GM-CBMeMBer 算法

GM-CBMeMBer 算法在CBMeMBer 滤波过程中引入了高斯混合模型化，将有限集RFS 作为全局研究目标，把传感器获得的量测当作全局量测，最终求出CBMeMBer 滤波中的封闭解。该算法将状态模型和观测模型变为有限集RFS 的模式，将多目标定位信号处理问题简化成宏观单目标估计的问题，从而避免了多目标的数据关联，大大降低了计算难度，但需要满足三个条件[12]：

1）每个运动目标的状态模型和观测模型要与式(1)(2)中所描述的保持一致，可改写为：

其中：Fk-1是k-1 时刻的状态转移矩阵；ζ表示k时刻的状态向量；Qk-1是k-1 时刻过程噪声协方差；Hk表示k-1 时刻量测矩阵；Rk是为k时刻的量测噪声；m、P分别表示高斯密度函数的均值和协方差。

2）目标的生存概率和检测概率即pS,k(x)和pD,k(x)为常值，其与目标的选取无关，且互相独立，即：

3）新生目标模型为随机有限集所描述的模型，每个目标航迹对应一个多伯努利项，每个状态对应一个高斯项。

GM-CBMeMBer 标准算法具体步骤为：

1）预测

假设k-1 时刻多目标密度为：

则预测的k时刻多目标密度为：

其中，

2）更新

若已知k时刻多目标密度为：

k时刻更新的多目标密度可显示为：

其中，

3 改进GM-CBMeMBer 算法

3.1 算法总体框架

算法总体框架如图1所示。为解决随机干扰信号统计特性未知的问题，在原有算法的基础上加入了衰减因子来改善Kalman 滤波器，实现噪声实时变化时作出动态调整，从而抑制滤波器发散。为了进一步改善滤波效果，引入了高斯项的剪枝合并来提高精度。

图1 系统流程图 Fig.1 System flow chart

3.2 具体内容

在含随机噪声预测的GM-CBMeMBer 滤波算法的基础上引入高斯项的剪枝合并，可以有效解决滤波器发散问题，提高滤波精度。具体步骤如下：

1）预测

假设k-1 时刻后验多目标密度仍然是式(7)形式的多伯努利密度，其概率密度为：

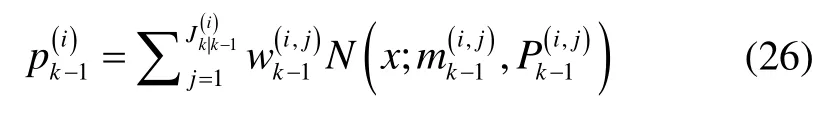
预测的多目标密度即式(8)中的密度，其中，

计算预测协方差时，引入自适应衰减因子可得：

2）更新

假设在时刻k，预测的多目标密度是式(13)中的多伯努利，则更新后的多目标密度可近似为式(10)中的多伯努利，其中：

其中，

预测测量值为：

3）自适应衰减因子选取

衰减因子核心在误差协方差和新息协方差，可得：

其中，λk为衰减因子，Pk|k-1为误差协方差，ak为标量因子，Ck为理论新息协方差，和为预测的误差协方差和新息协方差。

从式(19)可以得到加入衰减因子后的增益阵：

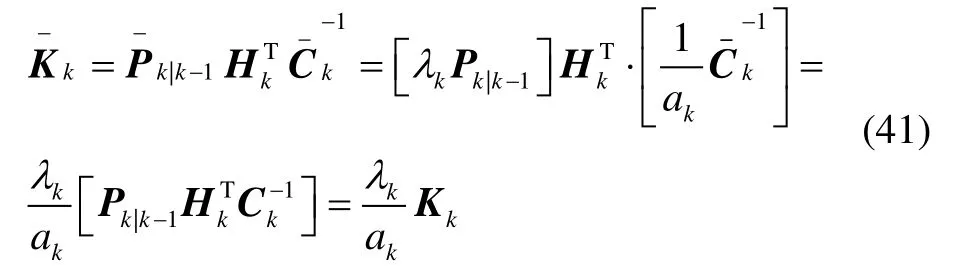
得到新的增益阵后，还需确定ak和λk的最佳值。

首先，根据式(41)可知，确定最佳的ak转变为求取，采用参考文献[16]中的方法确定，可得：

结合参考文献[17]的思想对其进行改进，可得：

其中：Yi为新息向量，从1 开始取值；λk-1为k-1 时刻的衰减因子。求得的能够更好地表示前一时刻衰减因子对当前新息协方差的影响。ak可以表示为：

确定衰减因子λk，可得：

其中，矩阵Pk|k-1和为对称、满秩矩阵，即为可逆矩阵。式(45)两边左乘右乘，可得：

若Hk可逆，得：

式(40)求得衰减因子预测协方差矩阵代入可得：

两边同时取迹，即：

4）适应衰减因子计算

传统自适应衰减因子的计算需要满足很多限制条件，这里做了改进。根据式(40)，可以表示为：

改进公式表示为当前误差的影响，如果目标模型不完善，信息的缺失会使得Pk|k-1和影响加强。根据式(50)可得，ak造成新息协方差的变化被认为是λk影响误差协方差得到的。所以，信息的缺失可以通过扩大误差协方差来实现，可得：

要求ak≥1 ，λk≥1。当误差协方差变化不大时，由于(1-ak)较小，可近似将(1-ak)Rk去掉；当误差协方差变化较大时，认为Rk较小，同样也可将(1-ak)Rk忽视掉。因而，无论Pk|k-1怎么变化，(1-ak)Rk都可以略去，所以可认为ak和λk相等，那么

得到基于自适应衰减因子的Kalman 滤波公式为：

最终可得新息协方差：

衰减因子为：

新的公式只需对新息作计算即可得到衰减因子，不要求矩阵是否可逆等限制条件，计算简单有效。

5）剪枝合并

由于预测过程中不断产生新生目标以及更新期间需要不断进行航迹假设确认，此时如果对高斯项数目没有限制，则会造成它们数目无限制增加。因此，在更新步骤之后，有必要添加修剪和合并过程：

①由于高斯项的数目会无限制增加，因此设定高斯项数目最大门限值Tmax，将多余的高斯项数目去掉。

②设置无人机航迹的门限值T_threshold，删除存在概率小于门限值的假设航迹。

③对于保留的假设航迹，设定修建高斯项门限elim_threshold，将低于此值得全部删掉。保留大权值高斯项，对于高斯项权值相近或者相同的取平均值。

4 实验结果

4.1 参数设置

通过无人机之间相互定位采集到数据，由于定位信号通信过程中不可避免受到噪声的影响，再利用GM- CBMeMBer 算法进行自适应滤波估计。测量时间长度T=100 s，测量时间间隔为Δ=1 s，检测区域为x-y的二维平面区域为[-1000 m,1000 m]×[-1000 m,1000 m]，检测面积为S=4×106m2，只考虑二维水平面，不考虑无人机飞行高度变化。假设在检测时间内，无人机多目标航迹模型为线性模型，运动模型为CV 模型。表1为无人机多目标信号预设轨迹给定的参数值。

表1 多目标信号参数 Tab.1 Multi-target signal parameter

状态模型和量测模型与式(1)(2)一致，其中，状态向量维度xdim= 4，量测向量维度zdim= 2。状态转移矩阵Фk-1、量测矩阵Hk、过程噪声方差矩阵Qk-1、量测噪声方差矩阵Rk为常矩阵；过程噪声强度σv=5，杂波强度λc=10。具体参数设置如下：

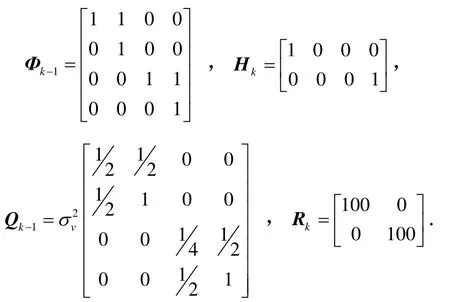
新生目标模型为多伯努利随机有限集[0;0;0;0]，参数（存在概率、高斯项权重、高斯项均值和高斯标准型）如表2所示。

其他参数目标的存活概率pS,k=0.90，检测概率PD,k= 0.98；每个航迹最大高斯项数目Lmax=100，修剪航迹的门限T_th=1e-3，修剪高斯项的门限elim_th=1e-5，融合高斯项的门限数merge_th=4。

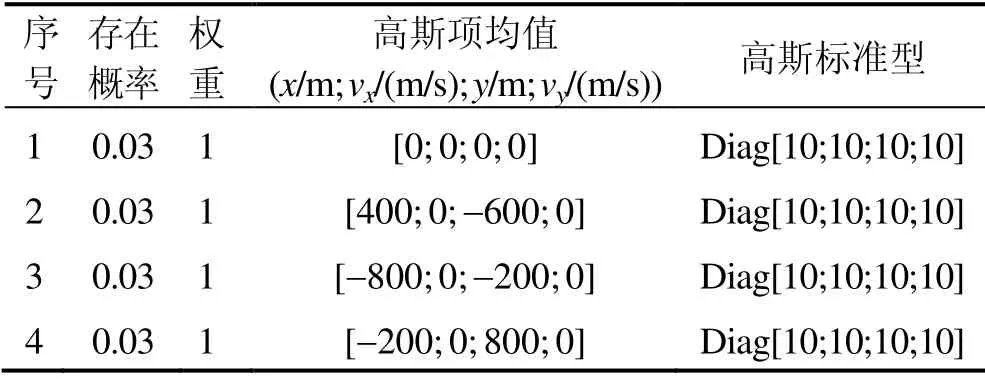
表2 新生目标参数 Tab.2 New target parameters

4.2 原始航迹及滤波结果

图2给出集群无人机的飞行航迹的仿真轨迹，共四组12 架次，每组从本组的同一起始点出发飞向不同方向，处于平飞巡航状态。图3为12 条无人机航迹在无噪声条件下的真实状态，分别是x、y方向上的航迹。图4和图5分别为标准算法和改进算法中真实航迹和 滤波航迹的对比图。虽然标准算法的实际值和估计值很接近，但不可避免有杂波点，在改进算法中能够明显看出杂波点有所减少。

图2 集群无人机飞行航迹 Fig.2 Flight path of Clustering UAVs

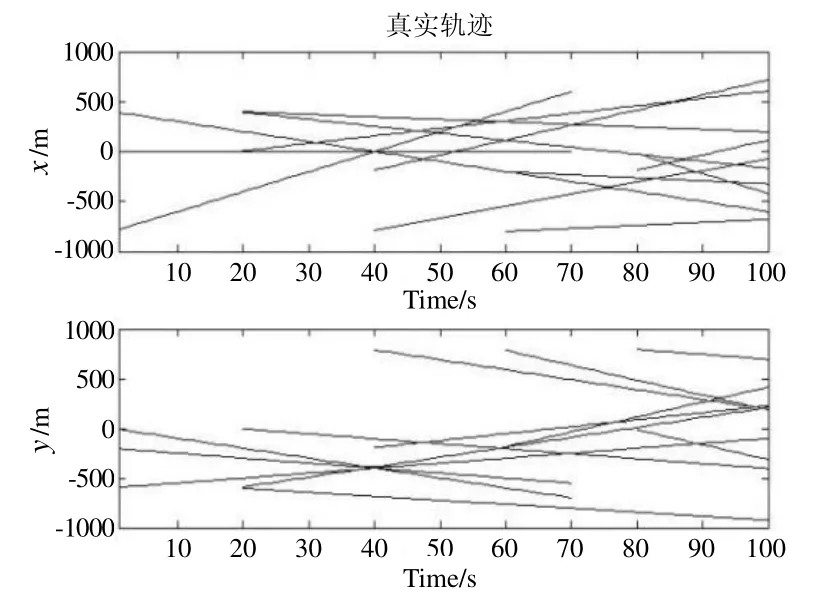
图3 实际航迹图形 Fig.3 Actua l track graph

图4 标准算法滤波结果 Fig.4 Filtering results of standard algorithm

图5 改进算法滤波结果 Fig.5 Filtering results o f the improved algorithm

4.3 滤波结果误差统计分析

如图6所示，(a)和(c)为标准算法在x和y方向上误差，(b)和(d)为改进算法在x和y上的误差。以每条航迹为研究对象，航迹上100 个有效点的平均差的绝对值构成了图5中的误差统计。可以看出，改进算法在12 条集群无人机航迹上的误差均低于标准算法，且定位信号滤波后杂波点也大幅度减少，经计算总体误差降低26.6%，验证了本文算法滤波效果更好。

表3是对滤波后杂波情况的统计结果，展示12条无人机航迹中共720 个点在x,y方向上的杂波情况。通过对比两种算法可以看出，改进算法在x、y方向上杂波率分别下降了5.41%和4.59%，从滤波后噪声干扰角度验证了改进算法的可行性，改善了滤波效果。

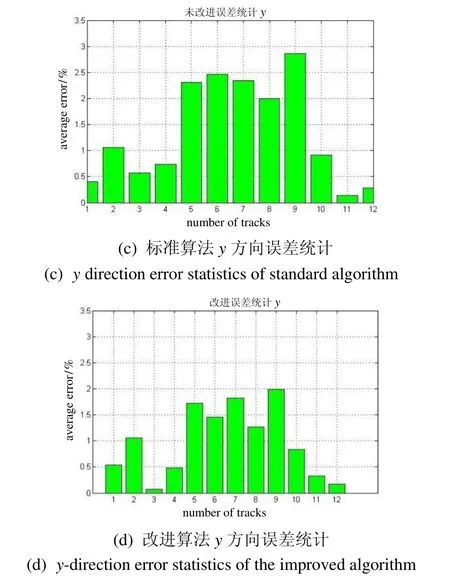
图6 误差分析 Fig.6 Error Analysis

表3 杂波统计 Tab.3 Clutter statistics

5 结 论

1）本文提出了一种集群无人机定位自适应滤波算法。通过在GM-CBMeMBer 滤波算法的基础上，引入衰减因子，实现在随机噪声的干扰下对噪声动态调整，引入高斯项的剪枝合并来提高精度。

2）通过与文献[7]进行实验结果的分析比较可知，新算法总体误差下降了26.6%，杂波率在x、y方向上分别降低了5.41%和4.59%，滤波效果有明显提升。

3）本方法简单易行，便于工程实现。