基于IGOWLA算子及三元区间数相似度的区间型组合预测模型
2019-11-20杜康袁宏俊
杜康, 袁宏俊
( 安徽财经大学 统计与应用数学学院, 安徽 蚌埠 233030 )
0 引言
由于预测对象的复杂性和不确定性,利用单一方法进行预测其结果往往不够精确,甚至可能产生较大的偏差.为了解决这一问题,1969年Bates等[1]首次提出了组合预测方法.由于组合预测方法能有效地提高预测精度,因此受到国内外学者的关注.早期的组合预测模型主要研究的是实数型数据,但由于预测对象往往受很多不确定性因素的影响,因此区间型组合预测方法逐渐受到人们的重视.目前,区间型组合预测方法的研究主要分为以下3种: ①利用区间数的左、右端点或区间数的中点和半径构建组合预测模型.例如:文献[2]利用诱导有序加权几何平均(IOWGA)算子分别对区间数的左、右端点进行集结,以对数误差平方和作为准则构建了一种组合预测模型.文献[3]利用诱导有序加权平均(IOWA)算子分别对区间数的中点和半径进行集结,以相关系数作为准则构建了一种组合预测模型.文献[4]利用区间数的中点和半径,并将灰色关联度作为准则构建了一种定权系数和变权系数的组合预测模型.②通过信息集成算子(COWA算子[5]、COWHA算子[6]等)将区间数转化为实数,然后利用该实数构建组合预测模型.例如:文献[7]提出了一种诱导有序加权连续区间广义有序加权平均(IOWC-GOWA)算子,然后利用该算子将区间数转化为实数,并选取指数支撑度作为准则构建了一种组合预测模型.文献[8]提出了一种连续区间有序几何加权平均Power(COWG -WPA)算子,然后利用该算子将区间数转化为实数,并选用广义绝对误差λ次和作为准则构建了一种组合预测模型.文献[9]利用诱导连续有序加权平均(ICOWA)算子将区间数转化为实数,并通过引入Theil不等系数构建了一种组合预测模型.③将区间数进行等价转化,目前相关研究主要是先将区间数转化为联系数,然后利用该联系数构建组合预测模型.例如:文献[10]首先将区间数转化为二元联系数,然后利用诱导有序加权调和平均(IOWHA)算子分别对二元联系数的同部和异部进行集结,并选取向量夹角余弦作为准则构建了一种组合预测模型.文献[11]也先将区间数转化为二元联系数,然后选取联系数贴近度作为准则构建了一种组合预测模型.由于上述前两种研究方法没有充分利用区间数的信息,因此其构建的组合预测模型的预测精度相对较低.基于此,本文利用第3种研究方法将传统的区间数转化为三元区间数,以此构建一种新的区间型组合预测模型,并通过实例分析验证该模型的有效性.
1 基本概念
定义1[12]43若X=[al,au]={x|al≤au,al,au∈R}, 则称X为二元区间数,简称为区间数.其中,al和au分别表示区间数的左端点和右端点.当al=au时,区间数退化为一个实数.若Y=[al,a*,au]={y|al≤a*≤au,al,a*,au∈R}, 则称Y为三元区间数,又称三参数区间数.同理,al和au分别表示三元区间数的左端点和右端点,a*表示在区间范围内取值可能性最大的点,称为三元区间数的重心.另外,当al=a*=au时,三元区间数退化为一个实数.
定义2[12]44设a=[al,a*,au]和b=[bl,b*,bu]为任意两个非负三元区间数,则a和b之间有如下运算关系: ①a=b⟺al=bl,a*=b*,au=bu; ②a+b=[al+bl,a*+b*,au+bu]; ③ab=[albl,a*b*,aubu]; ④μa=[μal,μa*,μau],μ>0.
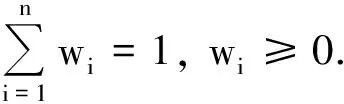
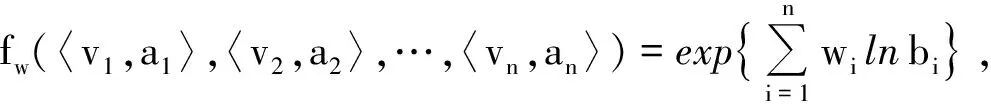
定义4[14]设a和b为正三元区间数,a=[al,a*,au],b=[bl,b*,bu], 则称
为a和b的相似度.
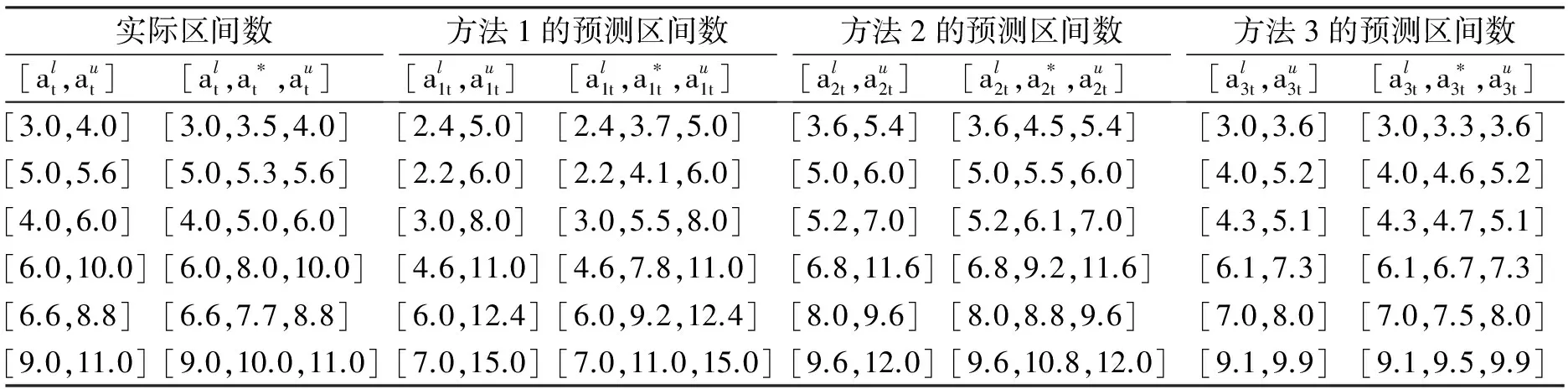
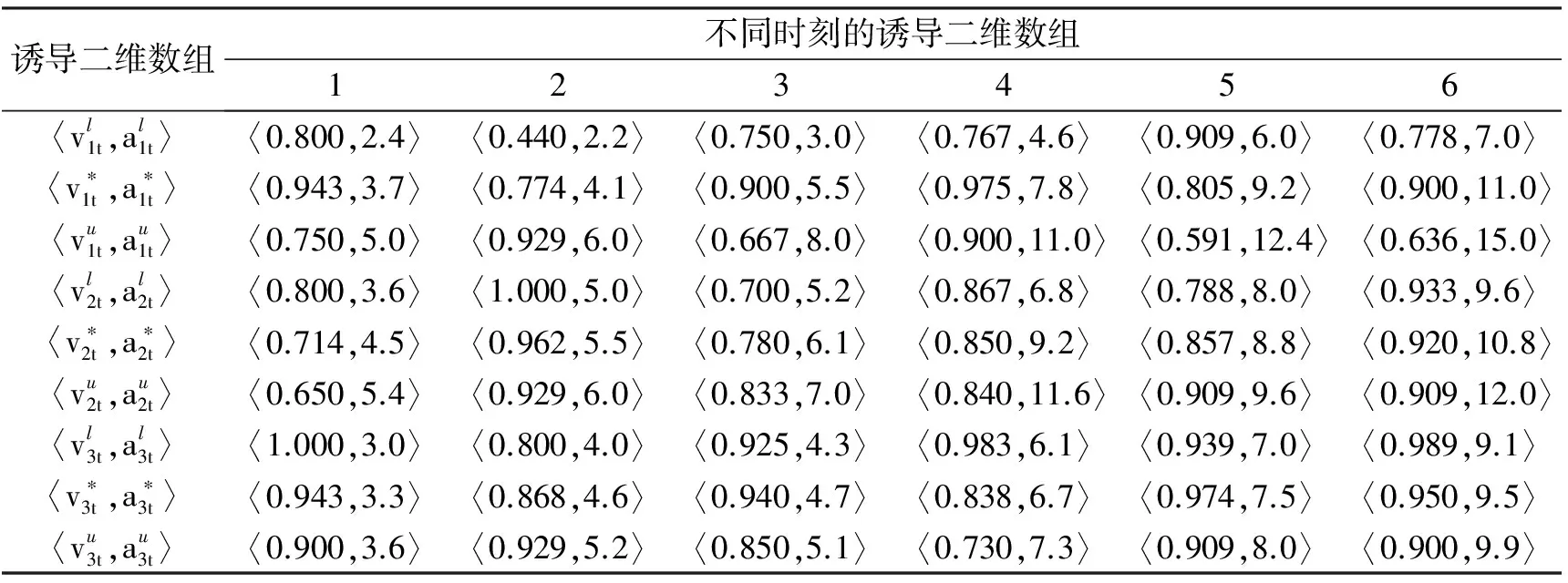
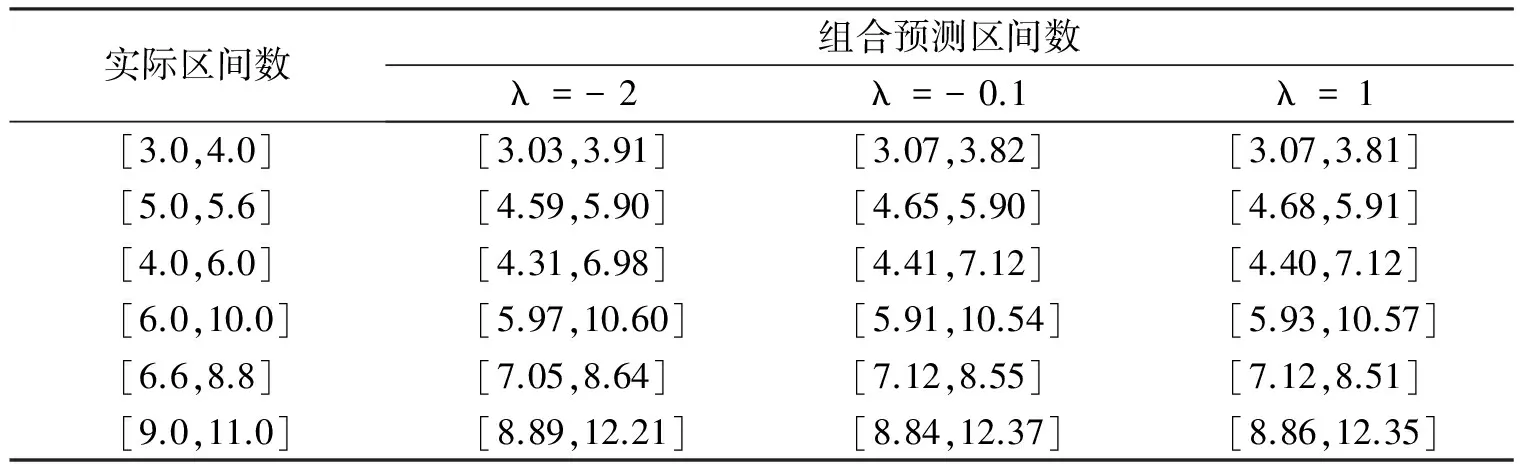
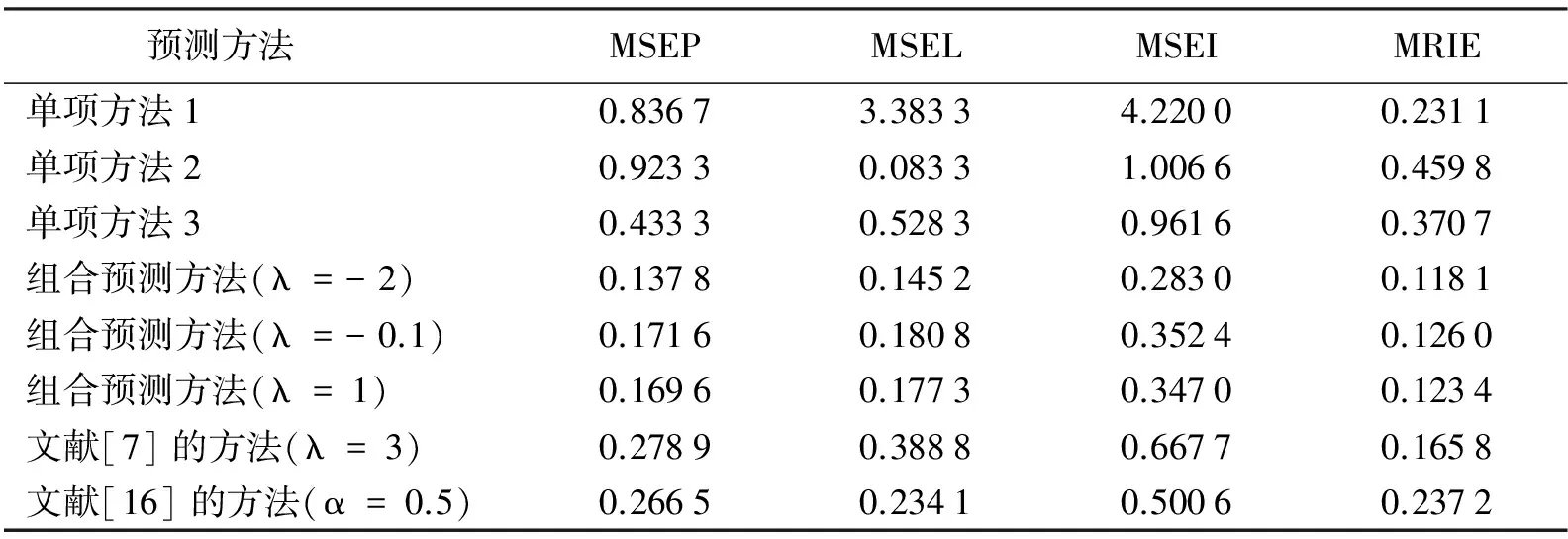
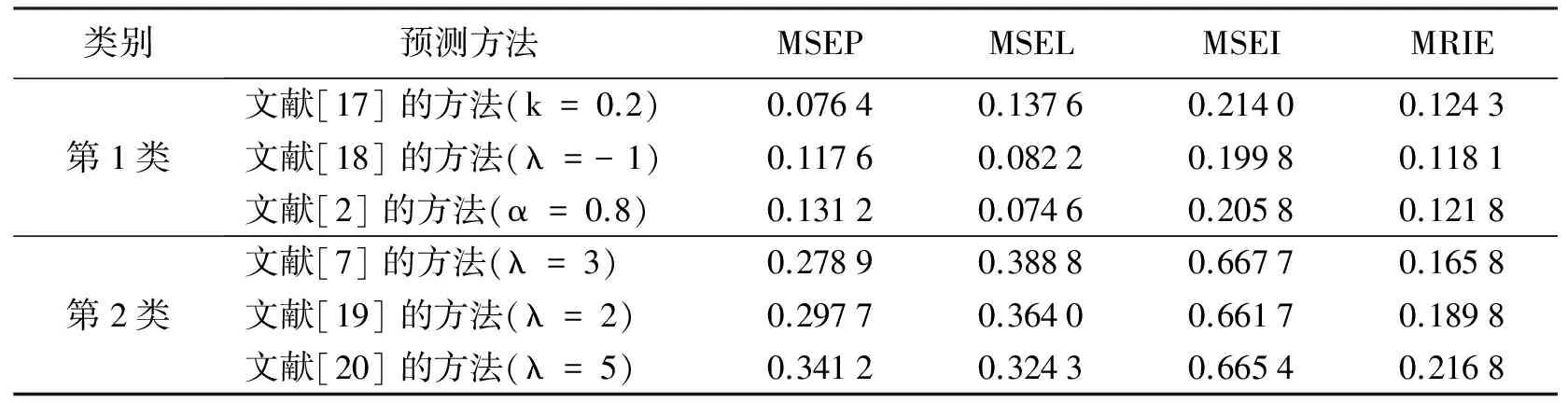
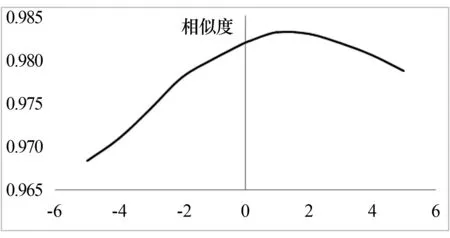
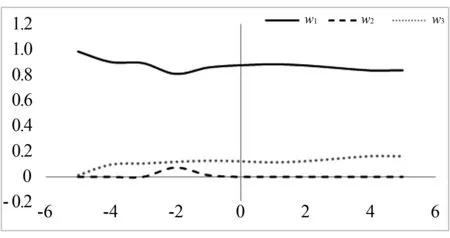
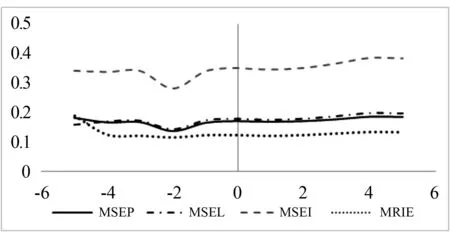
根据定义4可知,s(a,b)具有性质: ① 0 证明由三元区间数相似度的定义可知,上述性质②和③显然成立.下证性质①.不妨设(al)2+(a*)2+(au)2≥(bl)2+(b*)2+(bu)2, 则可得 (Ι) 模型(I)的加权系数向量(W=(w1,w2,…,wm))可以通过Lingo或者Matlab软件进行求解. 定义8设smin=mins(Yi t,Yt),smax=maxs(Yi t,Yt), 若: 为了验证本文提出的区间型组合预测模型(Ι)的有效性,选用文献[15]中的数据对其进行实例分析,数据见表1.评价指标选用平均区间位置误差平方和(MSEP)、平均区间长度误差平方和(MSEL)、平均区间误差平方和(MSEI)以及平均区间相对误差和(MRIE),各指标的计算公式为: 表1 区间数及其等价的三元区间数 根据定义5可分别求得3种单项预测方法在不同时刻的左精度、重心精度、右精度及其所诱导的二维数组,结果见表2.根据定义7可分别求得3种单项预测方法的三元区间预测值序列与实际三元区间数序列的相似度,结果见表3. 表2 3种单项预测方法在不同时刻的诱导二维数组 为了计算方便,首先利用Lingo软件计算不同λ取值下的加权向量W, 然后根据定义7计算组合预测方法的三元区间预测值序列与实际三元区间数序列的相似度,结果见表4. 根据定义6,可以计算出不同λ取值下的组合预测区间数,结果见表5. 表3 3种单项预测方法的三元区间预测值序列与实际三元区间数序列的相似度 方法1方法2方法3相似度0.86290.87140.9107 表4 不同λ取值下组合预测方法的加权系数以及相似度 表5 实际区间数和不同λ取值下的组合预测区间数 根据上述4种误差指标的计算公式,分别计算单项预测方法以及本文所提出的组合预测方法的MSEP、MSEL、MSEI和MRIE,结果见表6. 表6 不同预测方法的误差指标值 利用表3、表4和表6中结果,可从以下2个方面对区间型组合预测模型(Ι)的有效性进行判定: ①从三元区间数的相似度方面看,区间型组合预测模型(Ι)的相似度明显大于单项预测方法的相似度,且均大于单项预测方法相似度的最大值,这说明区间型组合预测模型(Ι)是优性组合预测模型; ②从4种误差指标值来看,区间型组合预测模型(Ι)的误差指标值显著低于各单项预测方法,且低于文献[7]和文献[16]中的方法,这说明区间型组合预测模型(Ι)不仅优于各单项预测方法,而且优于文献[7]和文献[16]中的组合预测方法.由此说明,本文所提出的基于IGOWLA算子及其相似度的区间型组合预测模型(Ι)是有效的. 为了进一步说明区间型组合预测模型(Ι)的优缺点,将模型(Ι)的误差指标值与引言中的前两类区间型组合预测模型的误差指标值(见表7)进行比较. 表7 两类区间型组合预测方法的4种误差指标值 由表6和表7可知,区间型组合预测模型(Ι)的预测精度略低于第1类区间型组合预测模型的预测精度,但二者都高于第2类区间型组合预测模型的预测精度.第1类区间型组合预测模型的预测精度虽然略高于区间型组合预测模型(Ι)的预测精度,但因为区间型组合预测模型(Ι)充分利用了区间的信息,所以相对更为可靠. 为了更加直观地观察参数λ对各单项方法预测的加权系数、 相似度以及4种误差指标的影响,对参数λ进行灵敏度分析,结果见图1 —图3. 图1 不同的λ值对相似度的影响 图2 不同的λ值对加权系数的影响 图3 不同的λ值对4种误差指标的影响 由图1可以看出:λ值对三元区间数的相似度影响较小,总体保持在(0.965,0.985)之间,并且当λ∈(-2,5)时,相似度相对最大,即此时区间型组合预测模型(Ι)的有效性相对最高.由图2可以看出,λ值对加权系数的影响较小,当λ≤-2时, 随着λ的增加,w1有所下降,w2和w3略微有所上升,且当λ>-2时,w1,w2和w3基本保持稳定.由图3可以看出,λ值对4种误差指标的影响也较小,当λ∈(-4,4)时,区间型组合预测模型(Ι)的预测效果相对最好.综上所述,为了使本文提出的区间型组合预测模型(Ι)的预测精度相对最佳,其参数λ的取值范围应在(-2,5)∩(-4,4)=(-2,4)上. 研究表明,本文基于IGOWLA算子及三元区间数相似度构建的区间型组合预测模型(Ι)的预测精度优于各单项预测方法和引言中所提的第1类、第2类区间型组合预测模型,因此模型(Ι)是一种优性组合预测模型,同时也为构建高精度的区间型组合预测模型提供了一种新思路.本文在模型(Ι)中只研究IGOWLA算子,并没有研究其他集成算子对该模型预测结果的影响;因此,今后将探讨不同集成算子对该模型预测结果的影响,以得到更高精度的区间型组合预测模型.2 区间型组合预测模型的构建
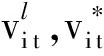
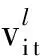
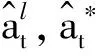
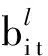
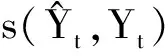
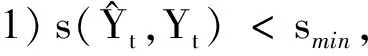
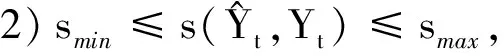
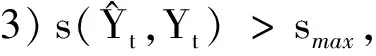
3 实例分析


3.1 比较分析
3.2 灵敏度分析
4 结束语
