纵向数据下部分线性模型的二次光滑估计

李生彪

( 兰州文理学院 教育学院， 甘肃 兰州 730000 )

0 引言

1994年， Zeger等[1]首次提出了纵向数据下部分线性模型：Yi j=βTXi j+g(Ui j)+εi j， 其中β是未知参数向量，g(·)是未知光滑函数.因部分线性模型结合了线性模型和非参数模型的特点，使得该模型具有很好的灵活性，且具有削减建模偏差、避免“维数祸根”和解释性强等优点，因而被广泛应用在计量经济学、生物医学等领域.目前，部分线性估计方法[2]是处理独立数据下变系数模型估计问题的常用方法，但其在部分线性模型的应用中时仍存在一些不足.例如：该方法只能在目标点的小区域内拟合直线段，因而使得该直线段导数的估计值没有得到有效利用，所得估计的渐近偏差的阶op(h2)偏大，存在稀疏问题，等等[3].对此，一些研究者对局部线性估计方法进行了一些改进，如HE等[4]提出了二次光滑局部线性估计.该方法通过再次光滑处理，整合目标点处的所有局部线性拟合值，使其在不改变渐近方差的阶的前提下，渐近偏差降低至op(h4)阶，且整体估计效果与局部立方回归估计相当，较好地克服了稀疏问题.此后，一些学者对二次光滑局部线性估计进行了进一步研究，但相关研究大多针对的是独立数据下的半参数回归模型估计[5-6]，很少运用于纵向数据的分析中.基于此，本文尝试利用二次光滑局部线性估计研究纵向数据下部分线性模型的估计问题，并对该方法的估计效果进行验证.

1 纵向数据下部分线性模型概述

纵向数据下部分线性模型有多种表达形式，本文仅研究如下形式的纵向数据下部分线性模型:

Y(t)=X(t)Tβ+g(t)+ε(t)，

(1)

其中ε(t)是均值为0的随机过程.假设观测n个个体，第i个个体观测mi次， 1≤i≤n.记ti j(1≤j≤mi)为第i个个体第j次观测时间，Yi j=Yi(ti j)为第i个个体在时间ti j的响应变量的观测值，Xi(ti j)为第i个个体在时间ti j的协变量的观测值.

2 纵向数据下部分线性模型的局部线性估计

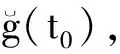
(2)

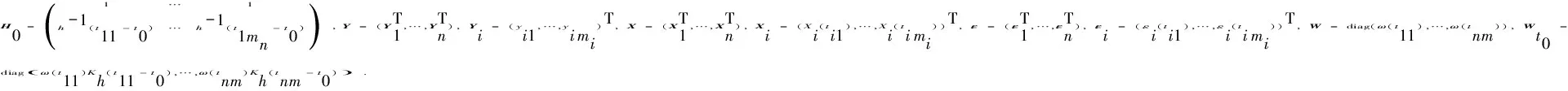
(3)

根据最小二乘理论可将模型(1)表示为(I-F)Y=(I-F)Xβ+ε, 其中I是n阶单位矩阵，F是仅依赖于ti j的光滑矩阵 (F可根据文献[7]指定).对上式应用Profile最小二乘法，可得到参数分量β的估计为

(4)

(5)

(6)

(7)

3 纵向数据下部分线性模型的二次光滑估计

(8)

其中h′是第2步光滑的带宽，L(·)是核函数，Lh′(·)=L(·/h′)h′，ω(ti j)是权函数.在此，本文取h′=h，L(·)=K(·)， 这样不但能简化结论形式，也能达到较好的估计效果.由于二次光滑局部线性回归估计存在边界问题，即在边界点处的渐近偏差不能像内点处的偏差那样减小，因此需要对边界点处的渐近性质进行单独考察.设观测的时间区间为[0，T]， 目标点t0∈[2h,T-2h]， 则边界区间为[0,2h)和(T-2h,T].再结合式(8)可得到改进的二次光滑局部线性估计表达式：

(9)

4 二次光滑局部线性估计的渐近性质

首先给出渐近性质证明中常用的正则条件[10]：

(C1) 核函数K(·)为具有紧支撑且有界的概率密度函数.为简化计算，在此假设K(·)具有对称性，即K(-x)=K(x).

(C3) 当n→∞时，nh8→0， 且nh2/(lgn)2→∞.

(C4)g(·)在内点处存在有界的四阶连续导数.

(C5) 对于∀t，λ(t)是二阶连续可微函数，X(t)是连续函数.

(C6) 对于∀t，σ2(t)=Var{ε(t)}有限，且二次连续、可微.

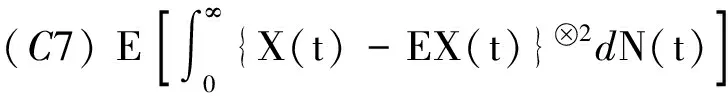
引理1在条件(C1)—(C3)下，有:

(10)

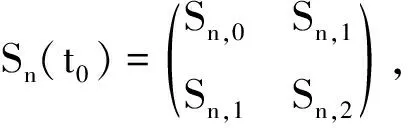
当h→0,nh→∞时,有

引理2在条件(C1)—(C4)下，有:

证明由于引理2中的3个式子的证明类似，因此在此只给出第1式的证明.由矩阵计算有

又因为K(·)是对称核密度函数，故有μ0=1，μ1=0.将μ0=1,μ1=0代入上式，第1式即可得证.

由于本文考察的是未知函数分量的估计效果，因此只给出引理3和引理4，不给出其证明.

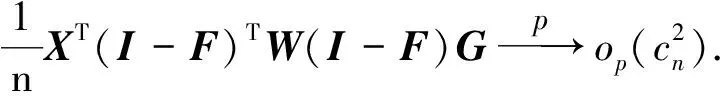
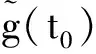
(11)

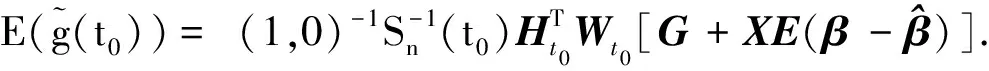
(12)

对向量G的每一分量运用Taylor公式[11],有

其中g(0)(t0)=g(t0)， 进而有

又因为K(·)是对称核密度函数，故有μ0=1，μ1=μ3=μ5=0.则上式可化简为

(13)

对式(10)进行计算可得

(14)

将式(13)和(14)代入式(12)得

进而有

(15)

显然式(15)的结果比式(6)更为精确.

于是有

(16)

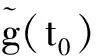
(17)

上式的第1部分即为

通过类似方法，可得式(17)的第2部分和第3部分的结果，分别为:

将这3部分的结果相加即可得证式(11).

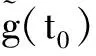
(18)

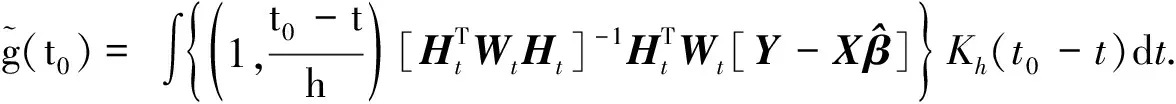
5 实例分析

实例分析的数据集(纵向数据)来自国际艾滋病研究中心记录的人体CD4细胞数的数据库，本文选取其中150个患者的检查结果.为了描述CD4细胞数损耗的平均时间趋势，建立如下纵向数据下部分线性模型：

Y(t)=β1X1+β2X2+g(t)+ε(t),

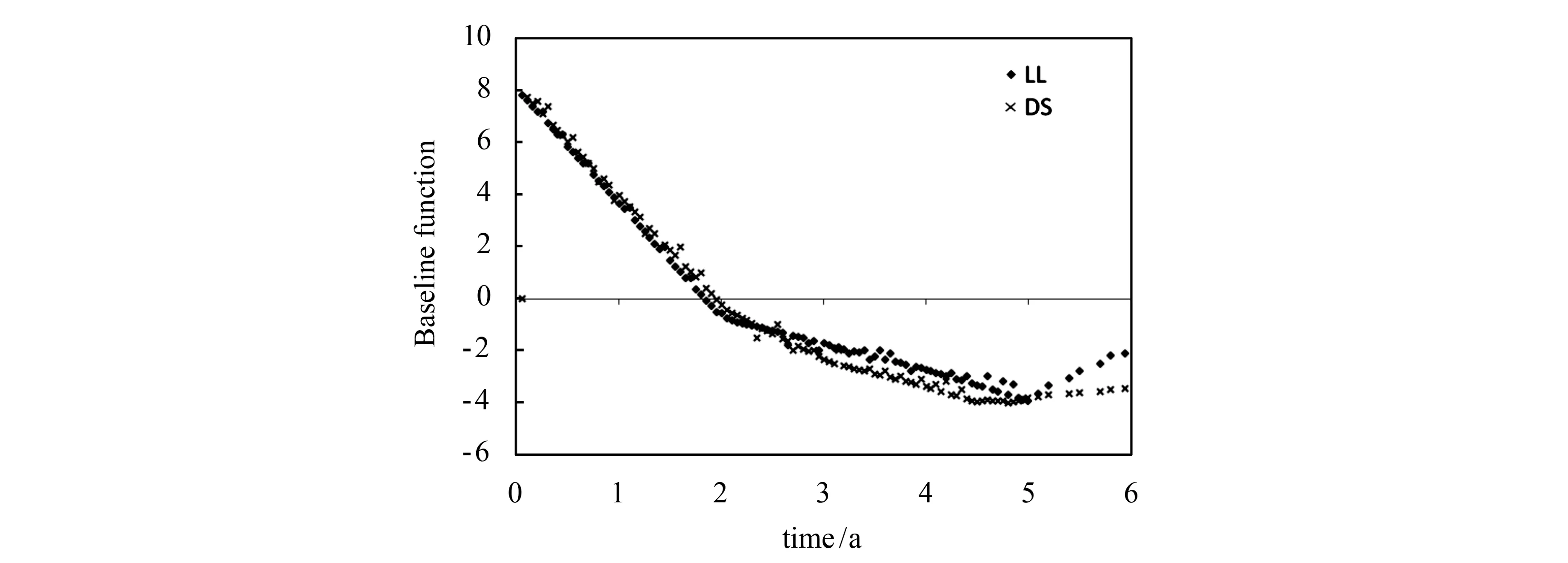
图1 非参数分量g(t)的估计曲线(LL为局部线性估计，DS为二次光滑估计)

由图1中2种估计曲线的走势可以看出，患者在感染HIV的初期，其平均CD4细胞浓度g(t)下降得很快，但在3年后下降趋势减缓.这两种方法的估计结果虽然在趋势上接近，但因二次光滑局部线性估计是在局部线性估计的基础上再次进行了光滑平均，所以其拟合曲线更为平滑.这表明二次光滑估计的整体效果优于局部线性估计，同时也证实了二次光滑估计可降低渐近偏差.