基于标签和协同过滤的改进推荐算法研究

金晶， 怀丽波

( 延边大学 工学院， 吉林 延吉 133002 )

0 引言

个性化推荐因有助于用户快速地获取所需信息，目前被广泛地应用于各种社交网络、音视频娱乐网站以及网络商务平台等.目前,推荐算法主要有协同过滤、混合推荐、基于内容和基于人口统计的推荐等[1],但这些方法普遍存在数据稀疏、冷启动和可扩展性的问题.为缓解算法中存在的冷启动和数据稀疏问题,一些学者对此进行了研究.例如：刘健以TF-IDF(term frequency-inverse document frequency)计算用户-标签相关度和项目-标签相关度的值,并依此构建了用户兴趣模型,提高了推荐精度[2]；蔡强等以TF-IDF方法分别生成用户和资源的标签特征向量来构造用户对资源的偏好矩阵，以余弦相似度(SIM)计算了资源相似性，该方法大大降低了计算的复杂度[3]71.针对标签无法准确地反映用户的喜好程度的问题，郭彩云等利用标签、用户评分值以及指数遗忘函数等评价指标捕捉了用户兴趣的变化程度，得到了较好的推荐效果[4].对于标签的语义歧义问题，李昊阳等用标签生成主题标签簇，然后通过对目标项目预测产生推荐目录，以此提高了推荐精度[5]； G.Pitsilis等使用标签聚类方法提高了推荐的准确性，并降低了信息过载[6].针对标签推荐中忽略项目和标签间具有相互作用的问题， Zheng Xiaolin等提出了一种可解释性的项目标签联合推荐方法，该方法不仅可提高推荐的准确性，同时也可缓解冷启动的问题[7].但在上述研究中，研究者均没有综合考虑评分数据和标签数据的作用，仍存在标签数据稀少的问题.基于此，本文在基于标签和协同过滤的个性化推荐算法的基础上，提出一种基于标签和协同过滤的改进推荐算法，并通过实验验证本文方法的有效性.

1 TCF算法介绍

1.1 基于标签的推荐算法

基于标签的协同过滤推荐算法(TCF)是在传统的协同过滤算法中引入标签因子，即通过标签反映用户偏好和项目特征的优势，以此改进推荐质量.在信息推荐时，标签通常被分成用户-标签、项目-标签两个部分来挖掘用户的喜好，并依此构造用户兴趣模型.

定义用户集合U={u1,u2，…,ui,…,um}，m为用户总数；标签集T={t1,t2，…,tk,…,tl}，l为标签总数.项目集I={i1,i2,…,ij,…,in}，n是项目总数.用户-标签相关度(UTu,t)的计算公式[3]70为：

(1)

其中Nmt代表打标签t的用户总数，Nu,t代表用户u打标签t的次数，Nlu代表用户u打标签的次数总和.

项目-标签相关度(ITi,t)的计算公式[3]70为：

(2)

其中Nnt代表被打标签t的项目总数，Ni,t代表项目i被打标签t的次数，Nli代表项目i被打标签的次数总和.

构建用户兴趣模型时先分别以公式(1)和(2)建立相关矩阵UTm ×l、ITn ×l， 然后再利用ITn ×l的转置矩阵TIl ×n计算用户ui对已有用户行为的项目ij的喜爱程度HPui,ij， 以此获得用户的历史兴趣矩阵HPm ×n.HPui,ij的计算公式[3]70为：

(3)

其中T(ij)是项目ij的标签集.

1.2 基于协同过滤的推荐算法

协同过滤推荐是指建立好用户兴趣模型后，以项目间的相似性预测用户ui对未操作项目ii的偏爱程度(PPui,ii),并以此构建矩阵PPm ×n.然后将PPm ×n的每行按照由高到低的顺序排序，取前N个进行推荐.协同过滤推荐的原理简单，因此目前被广泛采用在推荐系统领域中[8-9].PPui,ii的计算公式[3]71为：

(4)

其中NotI(ui)是用户ui未使用的项目集，I(ui)是用户ui的历史项目集,S1ii,ij是项目ii和ij的余弦相似度.

2 融入评分并扩展标签的TCF改进推荐算法

针对标签数据稀少的问题，本文提出一种基于标签和协同过滤的改进推荐算法(ITCF).首先利用项目-标签相关度构造项目特征向量，并结合评分构造用户-标签关联度，然后对用户的偏好标签集进行基于标签相似性和基于邻居用户偏好的扩展.

2.1 项目特征向量的构建

因为项目-标签相关度能很好地代表项目的内容特性，所以本文以项目-标签相关度ITij,tk表示项目ij的特征向量ij， 其定义为ij=(ITij,t1,ITij,t 2,…,ITij,tk,…,ITij,tl).该特征向量是构建项目-标签相关矩阵ITn ×l和项目相似矩阵S1n ×n的计算依据.构造项目-标签相关矩阵和项目相似矩阵的算法步骤如下:

Step 1 统计每个项目ij的标签集T(ij)和标签tk标记项目ij的次数nij,tk;

Step 2 记录项目总数n和step 1中的标签集个数N(T(ij));

Step 3 采用TF-IDF计算项目-标签相关度ITij,tk， 建立ITn ×l矩阵;

Step 4 取ITn ×l矩阵的任意两个行向量(即特征向量)进行余弦相似度计算，得到项目相似程度S1ii,ij并建立矩阵S1n ×n.

2.2 结合评分的用户标签关联度的计算

以用户ui打过标签的项目集I(ui)的评分集R(I(ui))表示用户ui的特征向量ui,ui=(rui,i1,rui,i2,…,rui,ij,…,rui,in).因为用户-标签相关度的大小通常与用户使用标签次数的多少和用户对该标签项目的评分高低有关，所以本文利用公式(5)来表示用户对标签的喜爱程度.

(5)

其中u是用户集中的用户，I(u)是用户u打过标签和评分的项目集，T(u)是用户项目集中含有的标签集，UTu,t是用户-标签偏爱程度，ITi,t是采取TF-IDF计算的项目-标签相关度.

建立用户-标签相关矩阵的算法步骤如下：

Step 1 统计每个用户u的未使用项目集NotI(u)、 使用过的项目集I(u)及对应的评分集R(I(u))， 并以R(I(u))表示用户的特征向量u；

Step 2 通过余弦相似度计算用户特征向量ui和uj的相似度S2ui,uj，并建立相似度矩阵S2m ×m；

Step 3 统计每个用户u使用过的标签集T(u)及未使用的标签集NotT(u)；

Step 4 以公式(5)计算用户-标签相关度UTu,t， 并以此建立UTm ×l矩阵.

2.3 用户偏好标签集的扩展

2.3.1基于近邻用户的标签扩展 用户在接受推荐时，因对兴趣相同的用户(即近邻用户)所推荐的项目更感兴趣，所以可以根据用户uj近邻用户的用户-标签相关度计算uj对没有历史行为的标签t的相关度UT1uj,t.本文将UT1uj,t的计算公式定义为：

(6)

其中UT1uj,t是经近邻扩充得到的用户uj对标签t的偏爱程度，Nei(uj)是与用户uj相似度最高的前K个用户组成的近邻集合，S2uj,ui是用户与近邻用户间的相似度.

基于近邻用户的标签扩展的算法步骤为:

Step 1 对S2m ×m的每行进行相似度排序，并取前K个相似的用户集Nei(uj)；

Step 2 统计邻居用户ui∈Nei(uj)使用过而用户uj未使用过的标签集T(Nei(uj))；

Step 3 利用公式(6)计算基于邻居用户标签的扩展用户-标签相关度UT1uj,t的值，并构建用户-标签矩阵UT1m ×l.

2.3.2基于标签相似度的标签扩展 本文根据标签相似度对用户-标签矩阵进行扩充，即根据标签的相似度引入用户对未有历史行为的标签的喜爱程度(UT2u,tj)， 其计算公式定义如下：

(7)

其中UT2u,tj是以标签相似度扩充的用户u对标签tj的喜爱程度，NotT(u)是不在原标签集里的标签，S3tj,ti是不在原用户标签集里的标签tj与原标签ti的相似度.

标签相似度的计算公式[10]为：

(8)

其中tj和ti表示两个不同的标签，I(ti)表示标签ti的项目集，ni,ti表示对项目i标注标签ti的次数.

基于标签相似度的标签扩展算法的步骤为:

Step 1 统计每个项目集I(ti)；

Step 2 利用式(8)计算标签间的相似程度S3tj,ti， 并建立S3l ×l矩阵；

Step 3 采用式(7)计算基于相似标签的扩展用户-标签相关度UT2u,tj的值,并构建UT2m ×l矩阵.

2.3.3融入标签扩展的用户-标签相关矩阵 本文将融入标签扩展的用户-标签相关度的计算公式定义为：

(9)

其中，TE1(u)是用户u基于近邻用户的标签扩展所得到的前E个标签组成的标签集，TE2(u)是基于标签相似度的标签扩展所得到的前E个标签组成的标签集，α是赋予UT1u,t的结合权重(用于UT1和UT2的信息融合).考虑到二者对预测用户-标签相关度的影响同样重要，因此本文将α取为0.5.由此得到的UT3u,t即为包含历史行为标签和扩展后标签的用户-标签相关度，其相关度的矩阵为UT3m ×l.

2.4 ITCF过程及算法描述

输入: 〈用户，项目，标签，评分值〉，邻居数K， 推荐个数N， 近邻用户、标签扩展标签数E.

输出: 输入的用户偏好的TopN推荐列表.

步骤1 按2.1中的步骤得到每个项目ij的标签集T(ij)、项目-标签关联矩阵ITn ×l、项目相似程度矩阵S1n ×n.

步骤2 按2.2中的步骤得到每个用户ui的历史项目集I(ui)所未使用过的项目集NotI(ui)、用户相似程度矩阵S2m ×m以及用户-标签关联矩阵UTm ×l.

步骤3 按2.3中的公式得到标签相似程度矩阵S3l ×l、综合扩展后的用户-标签矩阵UT3m ×l， 并赋值给UTm ×l.

步骤4 对ii∈NotI(ui)，ij∈I(ui),tk∈T(ij)，根据S1n ×n、UTm ×l和ITn ×l的转置矩阵TIl ×n，按照式(3)建立用户兴趣模型，按式(4)预测用户ui对未操作项目ij的偏爱程度PPui,ij，并以此构建矩阵PPm ×n.

步骤5 对PPm ×n的每行进行排序，记录所有行前N个标签的集合，由此得到推荐列表Rcmd(u).

3 实验结果与分析

3.1 实验数据与环境

实验采用MovieLens数据集(10 M)，实验环境为Intel 1.60 GHz CPU, 4.00 GB运行内存的PC机.

为了更准确地验证算法的有效性，实验选取标签数大于10的标签集，以排除冷门标签对用户和项目的影响.另外，为分析算法在稠密数据集和稀疏数据集下的性能，本文选取标签数量为前98位的用户和标签数在10～100的用户集来进行分析.数据集的分类如表1所示.

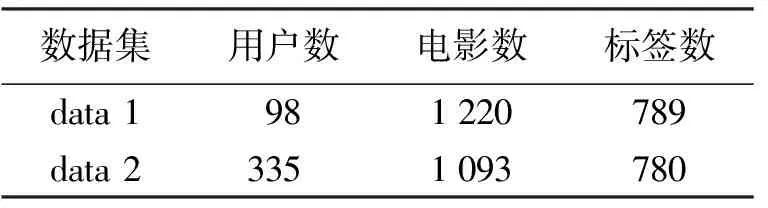
表1 数据集分类

3.2 评价标准

本文采用准确率(Recall)和召回率(Precision)对推荐算法进行性能评测，其计算公式如下：

(10)

(11)

其中U表示用户集，|Rcmd(u)|表示推荐集中的项目个数，|Test(u)|表示测试集中的项目个数，|Rcmd(u)∩Test(u)|表示两个集合的交集个数.

3.3 实验结果分析

根据文献[11]，测试每组样例集时，邻居用户数K取5， 扩展标签数E取40.推荐个数N的值分别取5、10、15、20、25、30、35、40和45进行测试，并与文献[2]和[3]中的两种TCF算法进行比较，实验结果见表2 —表5和图1 —图4.

表2 不同算法对data 1的准确率

表3 不同算法对data 1的召回率

表4 不同算法对data 2的准确率

表5 不同算法对data 2的召回率

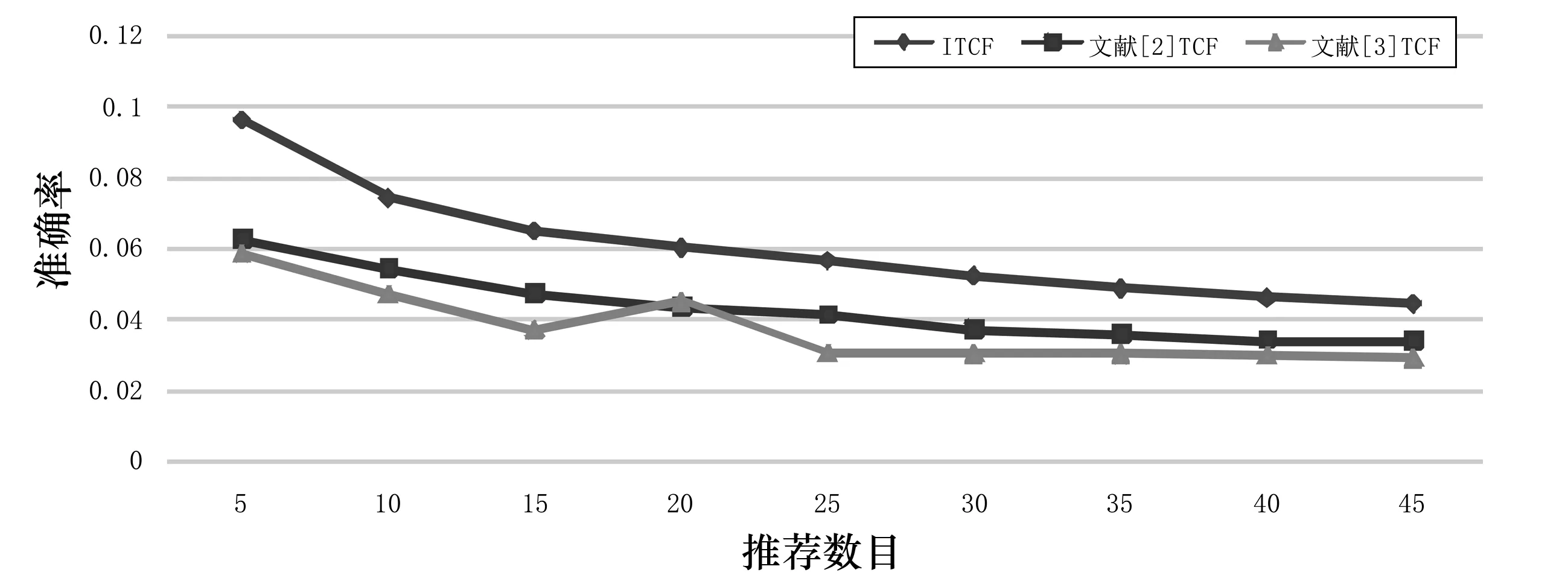
图1 不同算法对data 1的准确率

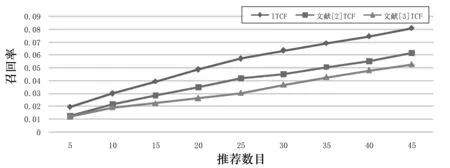
图2 不同算法对data 1的召回率

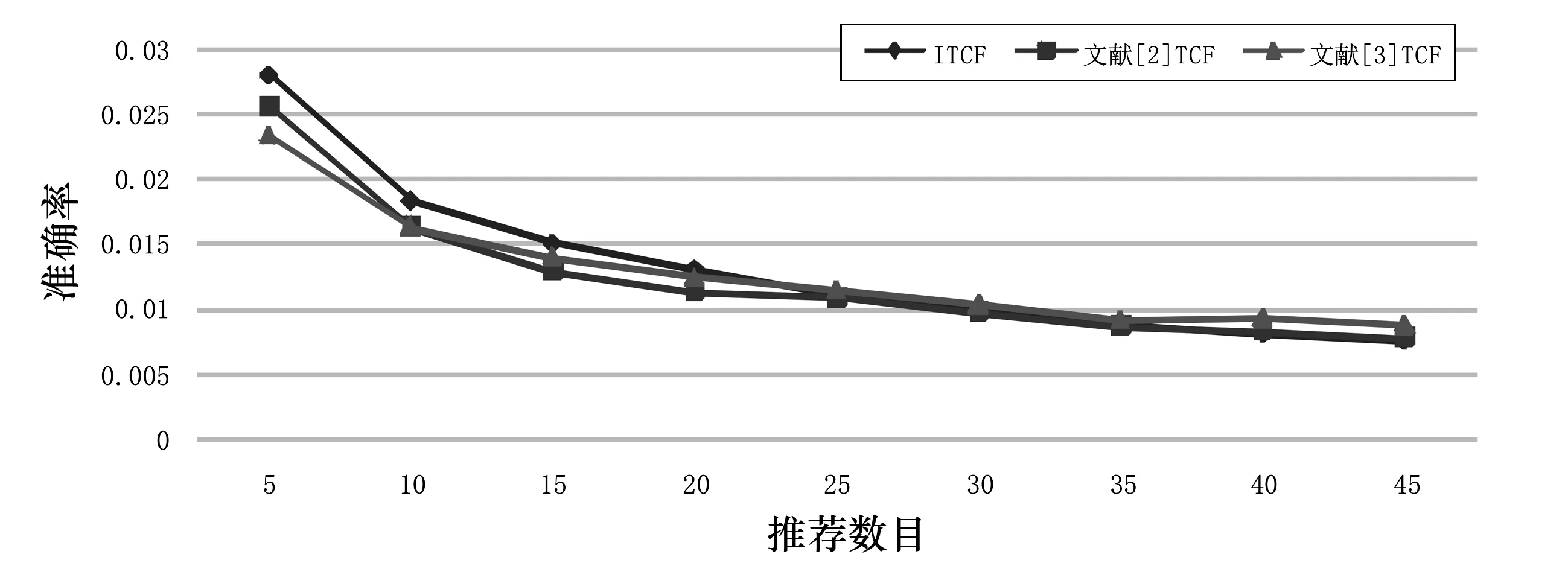
图3 不同算法对data 2的准确率

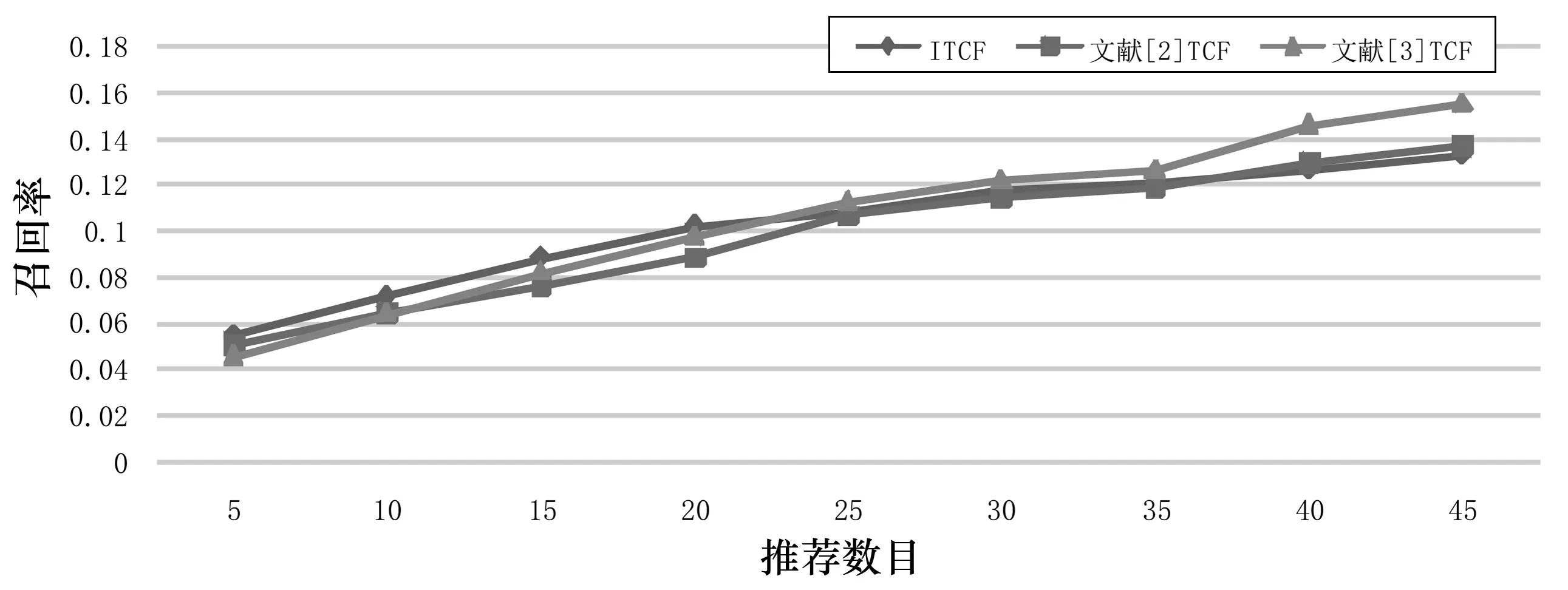
图4 不同算法对data 2的召回率

由图1和图2可以看出，在稠密的数据集中， ITCF的平均准确率和平均召回率比文献[2]和文献[3]的平均准确率和平均召回率分别提升约2.0%和1.7%.由图3和图4可以看出，在稀疏的数据集中，当5≤N≤20时， ITCF的准确率和召回率均高于其他两种TCF算法，其中准确率约提升0.2%，召回率约提升0.8%；N>20时， ITCF算法的准确率和召回率均略低于文献[3]的TCF算法，但与文献[2]的算法相近.其原因是当N>20时，数据集中的很多项目已不存在相似标签，因此导致ITCF的准确率和召回率降低.

Data 1的准确率和召回率比data 2的准确率、召回率提升得更高，其原因是由于data 1利用用户相似度和标签相似度扩充了用户-标签矩阵，因此在一定程度上缓解了数据稀少问题，进而提高了准确率和召回率.而data 2因用户历史行为数据过于稀少、训练样本不足，因此导致标签相似度普遍较低，进而使得其准确率和召回率提升幅度低于data 1.

4 结论

研究表明，本文提出的基于标签和协同过滤的改进推荐算法(ITCF)与文献[2 - 3]相比，其准确率和召回率均有所提高，因此本文方法对因标签过少而影响推荐质量的问题具有一定程度地缓解作用.本文在研究中未考虑用户兴趣的动态变化情况，在推荐实时性方面有所欠缺，因此我们在今后的研究中将引入时间因子，建立随时间变化的动态用户兴趣模型，以更好地完善本文模型.