基于改进粒子群优化算法和CRNN的多类SVM分类

俞颖， 黄风华， 阮奇

( 1.阳光学院 空间数据挖掘与应用福建省高校工程研究中心；2.阳光学院 人工智能学院； 3.阳光学院 教师发展中心： 福州 福建 350015 )

0 引言

支持向量机(support vector machine,SVM)[1]主要用于解决二类分类问题，而现实分类问题很多属于多类范畴，因此若将二类SVM应用在多类分类问题就需要对其进行参数优化和扩展.文献[2]采用蚁群算法对SVM进行了参数优化，该方法能在较短的时间内寻找到最优解，但计算量相对较大；文献[3]针对SVM优化对象设计了一种二进制编码基因串和相应的遗传算子，该方法虽然实现了SVM参数的组合优化，但需要解决个体基因的设计及编码问题；文献[4]利用蜂群的分工协作搜索最优蜜源来实现了SVM参数优化，该方法虽然可以实现局部和全局寻优，但时间开销较高；文献[5]提出了一种利用速度参数代替人工鱼步长的人工鱼群加速算法，该方法能够有效地克服参数优化后期难以逼近最优解的问题.文献[6-11]的作者利用改进的粒子群优化算法(PSO)对SVM的参数进行了优化，其研究结果均在一定程度上缓解了优化过程中可能出现的早熟和局部最优问题.

目前，将二类SVM扩展到多类分类场合的方法有两种：一是将原始的多类问题分解为多个二类问题，即通过构造多个二类分类器进行数据的“多次性”分类[12]；二是直接在目标函数上进行修改，将多个分类面的参数求解合并到一个最优化问题中，然后通过求解该最优化问题实现数据的“一次性”多类SVM分类[13].第1种方法使用的算法主要有“一对一”和“一对多”，这两种算法虽然简单，但存在无法确定某些数据点的具体类别或者某些数据点被划为多个类别的现象.第2种方法的优点是可利用少量的支持向量获取较高的分类精度，但其在模型训练过程中需要求解一个复杂的优化问题.基于上述研究，针对二类SVM在多类分类场合的应用中存在的问题，本文通过引入自适应调节技术及协作式递归神经网络(CRNN),提出一种多类SVM分类方法，并通过实验验证该方法的有效性.

1 多类SVM的基本原理

1999年，Bredensteiner等提出了一种多类SVM[13].该多类SVM的基本原理是根据给出的已知K>2类分类样本点，构造一个在类之间进行有效区分的决策函数.该方法主要应用于2个以上类别的大数据集分类问题，其优点是可以通过少量的支持向量获得很好的分类效果，但需要求解一个较为复杂的优化问题.假设一个多类分类问题的K类数据集为：

(x1,y1),(x2,y2),…,(xN,yN).

(1)

其中样本点xi∈Rn(i=1,2,…,N)，n为样本空间初始维度，N为样本数量，每个样本的种类由yi∈1,2,…,K表示，第i类样本数据集中包涵样本点的数量为mi.多类SVM构造区分函数的目的是尽可能地区别出每一类与剩余类别，其基本形式为：

fi(x)=ωTφ(x)-γi,i=1,2,…,K.

(2)

(3)

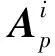
uT=[u12T,u13T,…,u1KT,u21T,u23T,…,uK(K-1)T].

K(x,y)=exp(-g‖x-y‖2).

2 IMPSO优化多类SVM参数

为了有效地克服传统PSO算法在SVM参数优化过程中容易出现的早熟收敛及陷入局部最优问题，本文采用自适应惯性权重结合自适应粒子变异来动态调节粒子的进化过程，以此实现对PSO算法的改进(该算法记为IMPSO).

假设在一个D维空间中，粒子i的位置以Xi=(xi 1,xi 2,xi 3,…,xi D)表示,速度以Vi=(vi 1,vi 2,vi 3,…,vi D)表示.在每一次迭代中，粒子i通过跟踪个体极值pbesti和群体极值gbest来更新自身的速度和位置.pbesti表示粒子自身找到的最优解，可以表示为pbesti=(pi 1,pi 2,pi 3,…,pi D)；gbest表示整个群体所找到的最优解，可以表示为gbest=(g1,g2,g3,…,gD).

在第d(1≤d≤D)维空间中，粒子的速度和位置的更新公式如下：

(4)

(5)

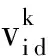
2.1 自适应惯性权重

自适应惯性权重的优化公式[14]为：

(6)

其中ωmin和ωmax为惯性权重的最小值和最大值，f为粒子当前的目标适应度值，favg和fmin分别表示当前所有粒子的平均适应度值和最小适应度值.自适应惯性权重ω能够随目标适应度值的变化而进行动态调整，在优化过程中可避免出现局部极小值，进而提高算法的搜索能力[15].

2.2 自适应粒子变异

为了实现动态调节每代粒子变异概率，本文在迭代过程中采用如下种群粒子概率变异方式：

1) ran d: 产生随机变异概率

2) 如果ran d>0.5

3)k=ceil(2*ran d)

4) ifk= =1

5)xi k=(20-1)*ran d+1

6) en dif

7) ifk= =2

8)xi k=(xgmax-xgmin)*ran d+xgmin

9) en dif

其中xi k为粒子i第k维的位置，g的区间为[xgmin,xgmax].

3 基于CRNN的多类SVM分类

CRNN由若干个递归神经网络(RNN)组成，其对解决约束性优化问题具有明显的优势[16-17].为了更高效地对“一次性”多类SVM分类问题进行求解，本文将原始多类SVM分类问题进行分解，并设计一个CRNN用于多类SVM学习，以此实现分类.本文将原始多类SVM分类问题分解成2个子问题,即求解支持向量u的二次规划问题和求解偏差γ的线性规划问题：

(7)

(8)

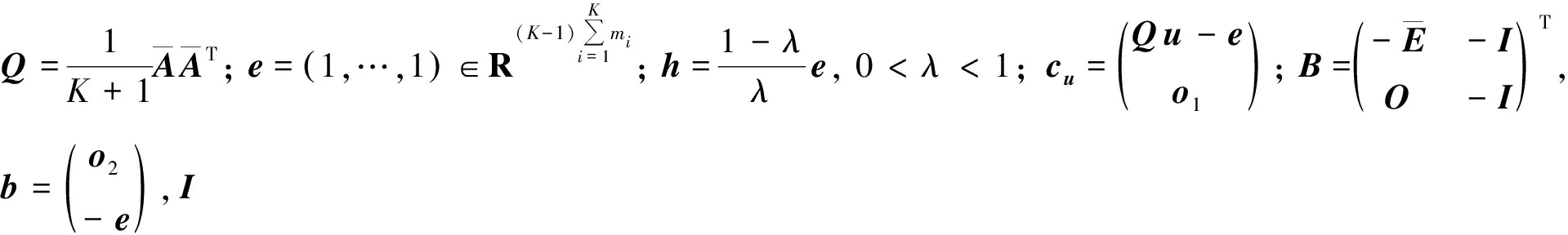
本文设计的CRNN由2个RNN自适应构造而成，其中一个RNN用于求解二次规划问题(7),记为RNN(9);另一个RNN用于求解线性规划问题(8),记为RNN(10).

(9)

(10)

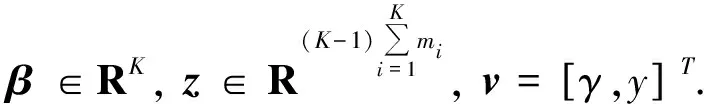
(11)

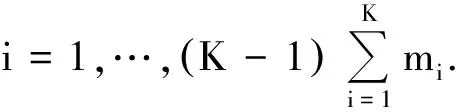
4 算法的流程

本文提出的多类SVM分类的算法流程为：

1)准备原始分类数据集Data，将其随机划分为训练集Data1和测试集Data2，并对训练集和测试集行归一化处理；

2)设定IMPSO算法的原始参数，包括迭代次数、种群规模、活动区间以及c1、c2、r1和r2等；

3)随机产生粒子的位置和速度，设置惯性权重的初始值，计算初始适应度值；

4)自适应更新粒子的惯性权重和更新粒子的速度和位置，然后对粒子进行自适应变异，并计算其适应度值;

5)更新个体极值pbesti和群体极值gbest；

6)判断是否超过最大迭代次数，如果是则获取最优多类SVM参数，转步骤7)；否则转步骤4)，继续迭代；

7)利用所设计的CRNN对问题求解：利用RNN(9)求解多类SVM的支持向量u，利用RNN(10)求解多类SVM的偏差γ；

8)构造决策函数(3)，通过计算函数(3)的最大值对待分类数据进行“一次性”分类；

9)利用分类结果计算分类精度和分析分类性能.

5 算法的实验验证

算法在Matlab R2014a环境下编程实现.为了验证本文所提出算法的性能，将本文提出分类算法的性能(记为IMPSO_CRNN_SVM)分别与其他3种算法(未进行参数优化的原始SVM算法(记为SVM)、基本PSO进行SVM参数优化的算法(记为PSO_SVM)、未进行PSO参数优化基于CRNN的多类支持向量机(记为CRNN_SVM))进行对比.

实验中使用UCI数据库中的Iris、Wine及abalone 3个数据集对各算法的分类性能进行验证.表1为3种数据集的基本信息，表2为4种算法在相同数据集上测试所达到的分类精度(算法在同一数据集上连续运行5次所得出的精度平均值).表3为CRNN_SVM算法和IMPSO_CRNN_SVM算法在Iris及Wine 2种数据集上的运行时间效率对比.这2种算法的迭代次数为300，种群数目为30，学习因子c1=1.6，c2=1.5.

表1 实验数据集的信息表

表2 不同算法的分类精度

表3 不同算法的运行时间 s

由表2可以看出，PSO_SVM算法和IMPSO_CRNN_SVM算法的分类精度总体上高于SVM算法和CRNN_SVM算法，其中本文提出算法的分类精度相对最高.由表3可以看出，本文提出的算法在优化SVM参数时需要的时间相对略长，但分类器的训练时间低于CRNN_SVM算法.CRNN_SVM算法的训练时间相对较长的原因是其参数(经验值)的设置需要经过多次试验才能获取.

6 算法应用

图1 原始遥感影像图

为了进一步验证本文算法的有效性和实用性，将IMPSO_CRNN_SVM算法应用于遥感影像分类.验证选取的是1幅多光谱遥感影像图，图中包涵水域、林地、草地和裸地4个类别的数据(图1).该影像图共有6个波段，数据集的基准是wgs-84，影像的空间分辨率是30 m.

首先对遥感影像图进行目视解译，并在实验区中提取4个类别的样本点数据.每类数据量为300个，共计1 200个.然后将每类数据的样本点随机划分为训练集(50个样本点)和测试集(250个样本点)，并对其进行归一化处理.最后利用IMPSO_CRNN_SVM算法进行分类处理.通过IMPSO优化之后的SVM参数取值为：bestc=74.590 5，bestg=0.010 0.由CRNN构造决策数据得到的分类实验结果为：训练集正确率为100%，测试集正确率为97.7%.由此可以看出，本文提出的IMPSO_CRNN_SVM算法具有良好的分类效果.

利用本文提出的IMPSO_CRNN_ SVM算法、CRNN_SVM算法、PSO_SVM算法及SVM算法对实验区遥感影像进行分类识别，结果如图2—图5所示.

图2 基于IMPSO_CRNN_SVM算法的影像分类

图4 基于PSO_SVM算法的影像分类

图3 基于CRNN_SVM算法的影像分类

图5 基于SVM算法的影像分类

由图2—图5可以看出，IMPSO_CRNN_SVM算法在边界处理方面整体优于其他3种算法.其中：SVM算法对裸地的识别精度低于CRNN_SVM和PSO_SVM算法，但SVM算法对林地的识别精度优于CRNN_SVM和PSO_SVM算法；IMPSO_CRNN_SVM算法对林地的识别精度较高，但对裸地的识别精度相对较低.

7 结论

研究表明，本文提出的IMPSO_CRNN_SVM算法的分类精度优于未进行参数优化的SVM算法、基于传统PSO的SVM算法及未进行参数优化的基于CRNN的多类SVM分类方法，且可有效地避免粒子群优化算法在优化多类SVM参数过程中容易陷入局部最优以及“多次性”SVM分类可能存在的不可分区域的问题，因此IMPSO_CRNN_SVM算法具有很好的实用价值.在今后的研究中，我们将利用分布式并行处理技术进一步降低算法的计算代价，提高算法的训练效率.