“人教版”“四边形”教学方法探究
2019-11-19陈乐乐

摘 要:长方形、正方形是最基本的平面几何图形,是学习三角形、平行四边形、梯形等平面图形的基础。文章通过对相关教材的分析,提出了在教学中多角度利用点子图素材,开展活动探究,不断建构完善长方形正方形的特征。
关键词:长方形;正方形;点子图;活动
作者简介:陈乐乐,浙江省温州市籀园小学教师,研究方向为小学数学教学。(浙江 温州 325000)
中图分类号:G623.5 文献标识码:A 文章编号:1671-0568(2019)23-0105-02
“人教版”三年级上册中的“四边形”教学内容起承上启下的作用,所以教材内容编排、新旧教材的变化、教师该如何根据教材变化进行有效的教学,都需要重视。
一、教材编写及变化情况
笔者翻阅了2003版本与2013版本的“四边形”的教学内容,发现教材在内容上有较大的改变。
1. 单元标题呈现不同。2003版单元标题为“四边形”,安排在第三单元“多位数乘一位数”之前,而2013版单元标题为“长方形和正方形”,安排在第七单元“多位数乘一位数”之后。由此可见,变化有:内容凸显长方形正方形;习题设置范围加大,素材更丰富。
2. 学习素材呈现不同。2003版教材例题中学习材料呈现多个四边形,并为分类做准备,让学生在分类中认识不同四边形的特征。2013版本只呈现长方形和正方形,重点让学生主动探究归纳长方形和正方形的特征,使学生对它们的认识由表象到实质。
2003版本中只出现一次用钉子板围四边形的练习,2013版本中出现一次用点子图画四边形,还有一次是用格子图画长方形和正方形。提供的素材不同,操作方法也不同。从实践操作看,钉子板上围四边形,只要一围自然而然就产生了直边和角,所以学生对于四边形的认识就是一种感知认识;而2013版本的在点子图上或者格子图上画,学生要边操作边思考怎么画产生角和直边,对于学生认识四边形,特别是认识长方形、正方形的特征有直接的体验。
二、教学前学生情况
新旧教材中,变化之一就是出现了点子图,那点子图对学生的实际学习有什么正迁移或者负迁移呢?教学前有如下思考:①点子图为学生画四边形提供支点,但会不会限制学生的思维,使学生看到点子图只会想到长方形和正方形?②点子图上的点是不是更能凸显四边形的特征?③点子图是否可以规范学生的操作活动?
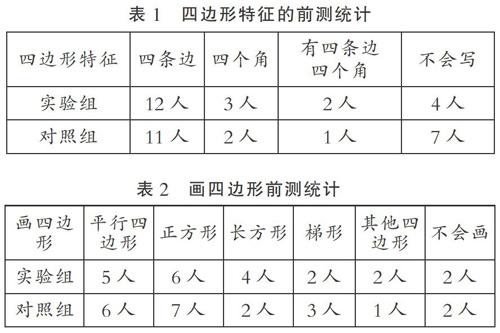
带着这些疑问,笔者进行了前测并进行了分析。将全班42人分成两大组,每组21人,一组同学当實验组,一组是对照组。前测题目如下:①实验组观察点子图上的四边形说一说四边形的特征;对照组根据白纸上的四边形说一说四边形的特征。②实验组在点子图上画四边形,对照组在白纸上画四边形。
结果分析如下(见表1、表2):
由前测结果可以看出:①让学生画四边形点子图不仅不会带来负迁移,更是规范了学生的画法;但对于认识四边形特征并没有特别明显的优势。②部分学生对于四边形有一定的了解,但他们所熟悉的知识是零散的,没有架构起零散的知识系统。
三、四边形认识的教学思考
1. 关注知识的前后关联,适当调整教学目标。在一年级下册,学生学过简单平面图形的认识,对于不同图形的特征有一定的了解。基于此,教师结合前测将2013版教材三年级上册的“四边形”内容定为认识四边形,特别是认识长方形和正方形,重点是对长方形和正方形特征的理解。教学目标的调整如下:
(1)知识与技能:让学生经历多种四边形的认识,寻找共性,概括四边形的基本特征并能辨析四边形;在活动探究中明晰长方形、正方形的特征,能从边、角两个维度加以概括。
(2)过程与方法:让学生经历“提出问题→大胆猜想→实验验证→得到结论”这一探究过程,引导学生主动观察、实验、猜测、验证、推理与交流等。
(3)情感态度与价值观:培养学生空间想象能力,感受数学的严密性,激发学生学习数学的兴趣。
2. 巧用点子图,感知四边形特征。点子图是由一行行、一列列相互对齐的点组成,每行、每列点与点之间的距离都相等。只有点没有线,能扩大学生的思维空间,所以借助点子图来让学生认识四边形尤为巧妙。四边形的特征“封闭图形”“四个角”“四条直边”是学生认识四边形、判断四边形的主要抓手。
(1)“四条直边”的认识。“四条直边”本质就是线段,可以度量长度,而点子图一个个点,形象直观地展现了这个特征,横竖斜的点子连接,有长度有方向,使学生对边的认识上升到线段。
(2)“四个角”的认识。从一点引出两条射线组成的图形就是角,而点子图里的一个个点,让学生认识四个角有点可依。
(3)“封闭图形”。点子图的前身就是格子图,格子图的密铺性促使点子图也具有该特征,点子图上一个个密铺的图形,使学生对封闭图形的认识更清晰。
3. 重视动手操作,完善知识结构。发展空间观念是“几何与图形”领域的重要目标之一,而空间观念是一种数学思考,这种数学思考必须有丰富的、形象的体验为基础,并在自主性的探究过程中得以发展。
因此,教师应设置实践活动,帮助学生一步一步构建长方形和正方形,让思维有螺旋式上升的梯度。笔者设置了如下活动:
(1)打破固有的思维。按照学生对于四边形的认识,长方形、正方形是有4条边,那是不是一定就需要四条边呢?给定一条边能确定长方形或者正方形吗?学生在操作中感受到,一条边不能确定一个长方形,长方形不唯一。但是,能确定一个唯一的正方形,感受正方形四条边相等、四个角都是直角的特征。
(2)树立全新的思维。再给定两根②号小棒,两根③号小棒(长度跟①号小棒一样),至少需要再选几根就能确定一个长方形?选1根②号会怎么样?选1根③号呢?让学生在操作中感知只要知道一条长一条宽就能确定一个长方形,从而掌握长方形对边相等、四个角都是直角的知识。
从“立—破—立”,让学生的思维在不断的调整中,建立长方形、正方形的思维模型,在探究中不断完善长方形和正方形的特征,在理解中感知长方形、正方形的特性。关注体验的形式和思考,可以帮助学生在头脑将表象与长方形、正方形特征之间建立联系。
参考文献:
[1] 葛素儿.方寸之间 独具一格——方格图在第一学段数学学习中的应用策略[J].教学月刊(数学小学版),2016,(11).
[2] 程佳丽.基于“格子图”的几何直观培养策略[J].教学月刊(数学小学版),2015,(4).
[3] 于蓉.小学数学“图形与位置”教材内容比较与分析[J].小学数学教育,2018,(20).
责任编辑 钱娜
