非负矩形张量最大奇异值的上下界
2019-11-19桑彩丽赵建兴
桑彩丽, 赵建兴
(贵州民族大学 数据科学与信息工程学院, 贵州 贵阳 550025)
非负矩形张量A的最大奇异值λ0(A)在固体力学中的强椭圆性条件[1]和量子力学中的纠缠问题[2]等诸多方面发挥着关键作用[3-7],尽管文献[5]给出了求解非负不可约矩形张量最大奇异值的含有正参数的迭代算法,但从文献[8]中得知,若能在利用该算法求得λ0(A)之前,给出λ0(A)的更精确的上界作为参数,则可以加速算法的收敛,因此,从这个角度来讲,研究非负矩形张量最大奇异值的上界估计也具有非常重要的意义.目前,对非负矩形张量最大奇异值的估计还不多见,就目前资料看,仅有一些初步结果[8-16],这些不足造成了张量奇异值理论的不完备,从而使其应用受到了限制.本文在文献[9]的基础上考虑非负矩形张量A的最大奇异值λ0(A)的上下界估计问题,并利用A的元素给出了λ0(A)的上下界,其中上界改进了文献[9]中的结果.
1 预备知识
令R(C)为实(复)数域,p、q、m、n为正整数,m,n≥2,N={1,2,…,n}.记A=(ai1…ip j1…jq),若
ai1…ipj1…jq∈R,
1≤i1,…,ip≤m, 1≤j1,…,jq≤n,
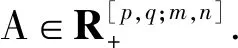
则称λ为A的奇异值,x和y为相应于λ的左、右特征向量,其中,l=p+q,Axp-1yq和y[l-1]为m维向量,它们的第i个分量分别为
xi2…xipyj1…yjq,
(x[l-1])i=xl-1i;
Axpyq-1和y[l-1]为n维向量,它们的第j个分量分别为
xi1…xipyj2…yjq,
(y[l-1])j=yl-1j.
记λ0(A)=max{|λ|:λ为A的奇异值},称其为A的最大奇异值.
最近,文献[9]中给出了最大奇异值的一个如下上界:
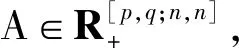
λ0(A)≤Ω(A)=
其中
[(ai…ii…i-aj…jj…j+rji(A))2+
[(ai…ii…i-aj…jj…j+cji(A))2+
且
Ri(A)-ai…ii…i,
ri(A)-aij…jj…j,
Cj(A)-aj…jj…j,
cj(A)-ai…iji…i.
弹性张量(当p=q=2,m=n=2或3时)在非线性弹性材料[1]中有着重要的应用.下面就m=n时,给出λ0(A)的上下界,其中上界改进了定理1的结果.
2 主要结果
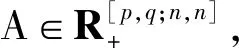
L(A)≤λ0(A)≤U(A),
其中
[(ai…ii…i-aj…jj…j+rji(A))2+
[(ai…ii…i-aj…jj…j+cji(A))2+

情形1假设xt≥ys,此时显然有xt≥yt.对任意给定的j∈N,j≠t,(1)式的第t个方程为
λ0(A)xl-1t=at…tt…txp-1tyqt+
atj…jj…jxp-1jyqj.
(3)
(i) 若xj≥yj,由(3)式可得
(λ0(A)-at…tt…t)xl-1t≤
λ0(A)xl-1t-at…tt…txp-1tyqt=
atj…jj…jxp-1jyqj≤
rjt(A)xl-1t+atj…jj…jxl-1j,
即
(λ0(A)-at…tt…t-rjt(A))xl-1t≤
atj…jj…jxl-1j.
(4)
若xj>0,由(1)式的第j个方程
λ0(A)xl-1j=aj…jj…jxp-1jyqj+
(5)
得
(λ0(A)-aj…jj…j)xl-1j≤
λ0(A)xl-1j-aj…jj…jxp-1jyqj=
即
(λ0(A)-aj…jj…j)xl-1j≤rj(A)xl-1t.
(6)
(λ0(A)-at…tt…t-rjt(A))(λ0(A)-aj…jj…j)≤
atj…jj…jrj(A).
(7)
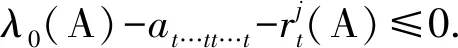
(ii) 若yj≥xj,由(3)式可得
(λ0(A)-at…tt…t)xl-1t≤
rjt(A)xl-1t+atj…jj…jyl-1j,
即
(λ0(A)-at…tt…t-rjt(A))xl-1t≤
atj…jj…jyl-1j.
(8)
若yj>0,由(2)式的第j个方程
λ0(A)yl-1j=aj…jj…jxpjyq-1j+
(9)
得
(λ0(A)-aj…jj…j)yl-1j≤
λ0(A)yl-1j-aj…jj…jxpjyq-1j=
即
(λ0(A)-aj…jj…j)yl-1j≤cj(A)xl-1t.
(10)
(λ0(A)-at…tt…t-rjt(A))(λ0(A)-aj…jj…j)≤
atj…jj…jcj(A).
(11)
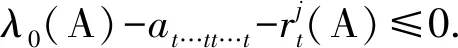
联立(7)和(11)式得
(λ0(A)-at…tt…t-rjt(A))(λ0(A)-aj…jj…j)≤
atj…jj…jmax{rj(A),cj(A)},
解得
[(at…tt…t-aj…jj…j+rjt(A))2+
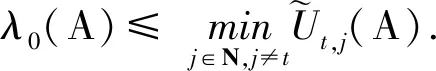

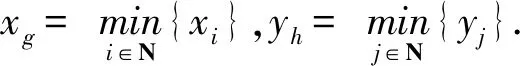
情形1假设yh≥xg,此时显然有yg≥xg.对任意给定的j∈N,j≠g,(1)式的第g个方程为
λ0(A)xl-1g=ag…gg…gxp-1gyqg+
agj…jj…jxp-1jyqj.
(12)
(i) 若yj≥xj,由(12)式可得
(λ0(A)-ag…gg…g)xl-1g≥
λ0(A)xl-1g-ag…gg…gxp-1gyqg=
agj…jj…jxp-1jyqj≥
rjg(A)xl-1g+agj…jj…jxl-1j,
即
(λ0(A)-ag…gg…g-rjg(A))xl-1g≥
agj…jj…jxl-1j.
(13)
由(5)式得
(λ0(A)-aj…jj…j)xl-1j≥
λ0(A)xl-1j-aj…jj…jxp-1jyqj=
即
(λ0(A)-aj…jj…j)xl-1j≥rj(A)xl-1g.
(14)
(λ0(A)-ag…gg…g-rjg(A))×
(λ0(A)-aj…jj…j)≥agj…jj…jrj(A).
(15)
(ii) 若xj≥yj,由(12)式可得
(λ0(A)-ag…gg…g-rjg(A))xl-1g≥
agj…jj…jyl-1j.
(16)
由(9)式可得
(λ0(A)-aj…jj…j)yl-1j≥cj(A)xl-1g.
(17)
(λ0(A)-ag…gg…g-rjg(A))×
(λ0(A)-aj…jj…j)≥agj…jj…jcj(A).
(18)
联立(15)和(18)式得
(λ0(A)-ag…gg…g-rjg(A))×
(λ0(A)-aj…jj…j)≥agj…jj…jmin{rj(A),cj(A)},
解得
[(ag…gg…g-aj…jj…j+rjg(A))2+
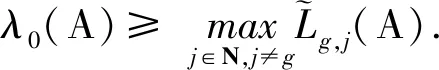
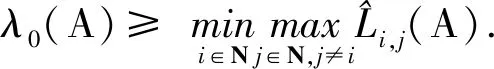
若A为可约张量,则应用类似于文献[4]中定理2的证明,可得结论成立.证毕.
由定理1、定理2,并应用类似于文献[9]中定理3的证明,易得如下定理.
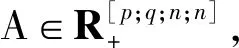
3 数值算例
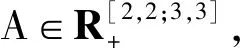
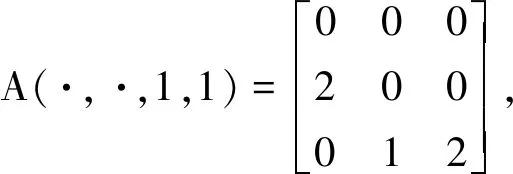
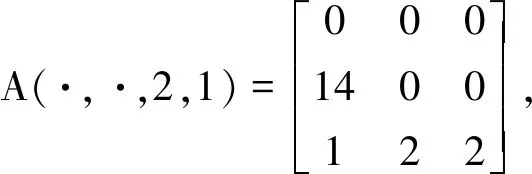
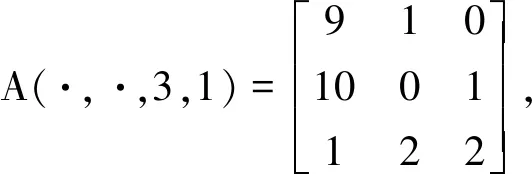
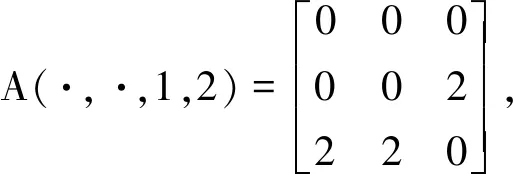
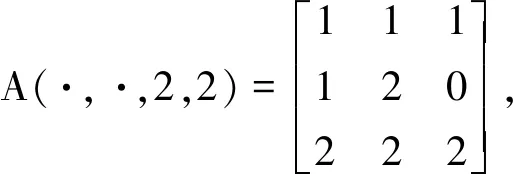
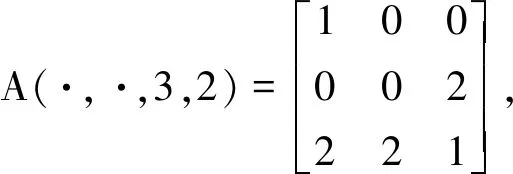
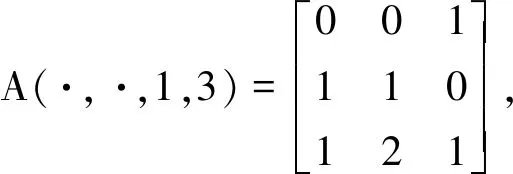

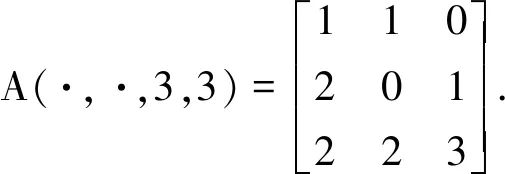
下面给出λ0(A)的上下界.由定理1得
λ0(A)≤46.
由文献[4]的定理4和文献[8]的定理3.2均得
18≤λ0(A)≤46.
而由定理2可得
19≤λ0(A)≤41.
事实上,λ0(A)=30.547 5.此例表明,由定理2得到的λ0(A)的上下界比由定理1、文献[4]的定理4和文献[8]的定理3.2得到的上下界精确.
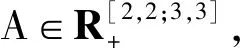
a1111=a1112=a1222=a2112=a2121=a2221=1,
其余元素均为零.由定理2得
3≤λ0(A)≤3.
事实上,λ0(A)=3.此例表明,由定理2得到的λ0(A)的上下界可以达到真值.
