Kronecker函数环对PvMD的一个新刻画
2019-11-19周德川王芳贵
周德川, 王芳贵, 胡 葵
(1. 西南科技大学 理学院, 四川 绵阳 621010; 2. 四川师范大学 数学科学学院, 四川 成都 610066)
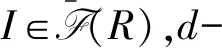
设*是R上的半星算子,对I∈F(R),若满足(II-1)*=R,则称I是*-可逆的.特别地,当*取为d-算子时,称d-可逆理想为可逆理想.若对任意I∈f(R),I都是*f-可逆的,称R是P*MD(Prüfer*-multiplication domain).特别地,当*取为d-算子时,即R的每个有限生成理想是可逆的,称R是Prüfer整环.
文献[3]引进了Kronecker函数环.令
g∈R[X]且c(f)*⊆c(g)*}.

1 主要结果
首先,回顾文献[8]中的一些概念.设J是R的有限生成理想,若J-1=R,则称J是GV-理想.用GV(R)表示R的所有GV-理想的集合.设M是无挠R-模,令M的w-包络为
Mw={x∈M⊗K|存在J∈GV(R),使得Jx⊆M}.
无挠模M称为w-模是指Mw=M.显然,对任意J∈GV(R),Jw=R.
设*是R上的星型算子,T是R的overring,若T=T[X]N*∩K,则称T是R的*-linked overring.T是R的*-linked overring等价于对R的有限生成理想I,若I*=R,则(IT)v=T(更多细节,参见文献[9]).
命题 1.1设T是R的overring,则T是R的w-linked overring当且仅当T作为R-模是w-模.更进一步,v-、t-及w-linked overrings这三者是一致的.
证明若T是R的w-linked overring,对任意α∈Tw,存在J∈GV(R),使得αJ⊆T.从而αJT⊆T,故α∈(JT)-1.J∈GV(R),故J-1=R.从而Jv=R,自然(JT)v=T.所以有(JT)-1=T,继而α∈T,故Tw=T.反之,假设Tw=T,对R的有限生成理想I,若Iw=R,则I∈GV(R).故T=Tw=(IT)w⊆(IT)w(T)⊆(IT)v⊆Tv=T,从而(IT)v=T,故T是R的w-linked overring.
对任意I∈f(R),有It=Iv,且It=R当且仅当Iw=R[10].因此,易知v-、t-和w-linked overrings三者一致.
由命题1.1可知vc=wc.
引理 1.2若J∈GV(R),则Jvc=R.
证明注意w≤vc[7].若J∈GV(R),则Jw=R,因此Jvc=R.
引理 1.3[3]若*是R上的一个e.a.b.的星型算子,则对任意f,g∈R[X]{0},c(fg)*=(c(f)c(g))*.
引理 1.4[10]若B是R[X]的有限生成理想,则B∈GV(R[X])当且仅当B∩R≠0且c(B)∈GV(R).
设T是R的w-linked overring,以防混淆,用w(T)表示T上的w-算子.对T-模M,用Mw表示M作为R-模时M的w-包络;用Mw(T)表示M作为T-模时M的w-包络.
命题 1.5Kr(R,vc)是R[X]的w(R[X])-linked overring.

设T是R的w-linked overring,对T的分式理想A,定义wR:A→Aw,则wR是T上具有有限特征的星型算子,即(wR)f=wR[10].
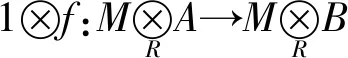
定理 1.6对整闭整环R,以下等价:
1)R是PvMD,
2)Kr(R,vc)是w(R[X])-平坦R[X]-模,
3)Kr(R,vc)是平坦R-模,
4)Kr(R,vc)是w-平坦R-模.
证明(1)⟺(2)R是PvMD当且仅当Kr(R,vc)是平坦R[X]-模[7].注意Kr(R,vc)是Bezout整环[3],则Kr(R,vc)的有限生成理想是主理想,因此是w(Kr(R,vc))-理想,故Kr(R,vc)的每个理想是w(Kr(R,vc))-理想[10],从而是w(R[X])-理想.由文献[14]的定理2知,Kr(R,vc)是平坦R[X]-模当且仅当对Kr(R,vc)的任意极大理想M,Kr(R,vc)M=R[X]M∩R[X],故由命题1.5及定义知Kr(R,vc)是w(R[X])-平坦R[X]-模当且仅当Kr(R,vc)是平坦R[X]-模.
(1)⟺(3) 由文献[7]的推论3.8知,Kr(R,vc)是平坦R[X]-模.由于R[X]是平坦R-模,故有文献[14]的引理2知,Kr(R,vc)是平坦R-模.
(3)⟺(4) 注意平坦模是w-平坦模.
(4)⟺(1) 由文献[10]的定理9.2.3知,只需证对R的极大w-理想m,有Rm是赋值环.
由文献[13]的定理2.1知,Kr(R,vc)Rm是平坦Rm-模.注意Kr(R,vc)Rm⊆Kr(Rm,b)及Kr(R,vc)Rm是Bezout整环,因此Kr(Rm,b)是平坦Kr(R,vc)Rm-模,Kr(Rm,b)是平坦Rm-模.由文献[1]的定理2.20知,Rm是Prüfer整环,故Rm是赋值环.
文献[15]引入了多项式环上的一个半星算子.设R是整环,K是其的商域,令R1=R[X],K1:=K(X)表示R[X]的商域.设*是R上的半星算子,令
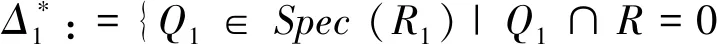
Q1=(Q1∩R)[X]且(Q1∩R)* fR*}.


*[X1,X2,…,Xr]:=(*[X1,X2,…,Xr-1])[Xr],
其中*[X1,X2,…,Xr-1]是R[X1,X2,…,Xr-1]上的具有有限特征的稳定半星算子.R[X]上与w-算子有关的算子有wR-算子及w(R[X])-算子,那么w[X]-算子与它们有什么样的关系,是否相等?本文就以讨论这三类算子的关系结束.为了解决这一问题,回顾文献[16-17]中的一些知识.R的所有理想构成的集合的子集F称为局部系统(localizingsystem)是指满足:
1) 若I∈F,J是R的理想且I⊆J,则J∈F;
2) 若I∈F,J是R的理想且对任意i∈I,(J:RiR)∈F,则J∈F.
局部系统F称为有限生成的,是指对任意I∈F,存在有限生成理想J∈F,使得J⊆I.
引理 1.71) 若*是R上的半星算子,则F*:={I|I是R的理想,且I*=R*}是一个局部系统;
2) 若*是R上的具有有限特征的半星算子,则F*是有限生成的局部系统;
4) 若F是局部系统,则F[X]={A|A是R[X]的理想,且A∩R∈F}是R[X]的局部系统;
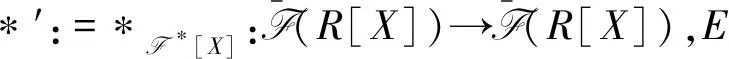
6) 若*是R上的稳定的具有有限特征的半星算子,则*′=*[X].
证明1)、2)、3)由文献[16]命题1.2知.4)由文献[16]命题3.1知.5)由文献[16]知.6)由文献[17]命题2.2知.
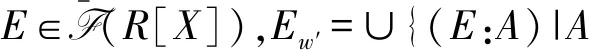
命题 1.8对R[X]上的3个半星算子wR,w(R[X]),w[X],有wR=w[X]≤w(R[X]).
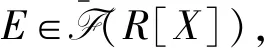
下面的例子说明w[X]≠w(R[X]).
例 1.9对整环Z[X],其中Z是整数环,考虑其理想(X,X2+1),可证(X,X2+1)w′≠(X,X2+1)wZ[X].X与X2+1互素,而Z[X]是最大公因子整环,故(X,X2+1)∈GV(Z[X]),从而(X,X2+1)wZ[X]=Z[X].若1∈(X,X2+1)w′,则存在Z[X]的理想A,满足(A∩Z)w=Z,且1∈((X,X2+1):A),从而A⊆(X,X2+1).而A∩Z⊆(X,X2+1)∩Z=0,与(A∩Z)w=Z矛盾.
由命题1.8知wR=w[X].那么对n≥2,是否也有wR[X1,X2,…,Xn-1]=w[X1,X2,…,Xn]?答案是否定的.下面例1.10说明wR[X1]≠w[X1,X2].
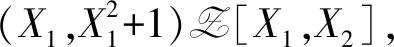
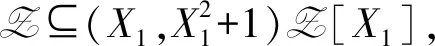
(A∩Z[X1])wZ=Z[X1]
矛盾.
致谢西南科技大学博士基金(17zx7144)对本文给予了资助,谨致谢意.
