基于G类函数的二元Copula函数的构造
2019-11-19吕王勇张琼文杨和柳
余 欣, 吕王勇, 张琼文, 杨和柳
(四川师范大学 数学科学学院, 四川 成都 610066)
1 引言及主要结果
早在1959年,Sklar在回答Frechet关于多维联合分布函数和低维边缘分布函数之间关系的问题时引入了Copula的概念.
Copula各种性质的研究是概率论与数理统计及其应用领域十分引人注目的课题之一,一直以来都受到统计学者的青睐.Copula函数作为刻画变量之间相依机制的工具,克服了传统的线性相关系数研究变量非线性关系的不足.迄今为止,已经有很多相关研究结果.文献[1]对Copula函数的含义和性质做了全面详细的介绍,文献[2]讨论了Copula函数中参数的矩估计方法和极大似然估计方法,文献[3]基于Copula函数研究2个变量的尾部相关,文献[4]比较了阿基米德Copula函数的几种参数估计方法,文献[5-6]对随机变量间的相依性展开研究,文献[7]从图像重构的角度提出广义Copula的概念.Copula在实际中应用广泛,文献[8]利用Copula函数对干旱特征进行了分析,为旱作农业生态管理提供依据.本文的主要工作是讨论二元Copula的构造.到目前为止,构造二元Copula主要是从变换和函数2个角度讨论.从变换的角度,通过Sklar定理的反演,直接从二元联合分布函数求得二元Copula函数;另一方面,许多学者从函数的角度出发,提出了若干构造二元Copula的方法.文献[9]提出利用连续可导的实值函数构造生成元,文献[10]研究了具有共同对角面函数的一类Copula的构造,文献[11]提出了一种新的函数:g函数,并基于g函数构造Copula.基于文献[12]给出的Copula的良好性质,文献[13]应用加权几何平均构造二元Copula,文献[14-15]分别提出了基于F类函数的一类二元Copula的构造,进一步扩充Copula的种类.本文从函数的角度考虑,提出一类新的函数:G类函数,基于定义的G类函数,提出了2种构造二元Copula函数的新方法.随着Copula理论的逐渐完善,Copula函数越来越多地被应用到金融风险管理、投资组合等研究领域,尤其是变量间相关性的度量上,但目前还没有文献将Copula函数应用到地区产值相关性的研究中.文献[16]讨论了四川省三次产业产值发展与经济增长的关系.基于此,本文利用构造的Copula函数对成都市和绵阳市第一产业产值间的依存关系进行了实证研究,分析不同地区产值间的相关性.
2 定义
定义 2.1[1]一个二元函数C(u,v)称之为二元Copula,如果C(u,v):I2→I=[0,1],并且满足:
1) 边界条件:C(u,0)=C(0,v)=0,C(u,1)=u,C(1,v)=v;
2) 2-增性:对∀0≤u1≤u2≤1有
VC([u1,u2]×[v1,v2])=C(u2,v2)-
C(u2,v1)-C(u1,v2)+C(u1,v1)≥0,
其中VC([u1,u2]×[v1,v2])称为函数C在矩形[u1,u2]×[v1,v2]上的体积.事实上,这个体积就是C在矩形[u1,u2]×[v1,v2]上的二阶差分,
定理 2.1(Sklar定理)[1]设H是一个联合分布函数,其边缘分布函数分别为F和G,那么一定存在一个CopulaC,使得
H(x,y)=C(F(x),G(y)),
如果F、G是连续的,则C唯一,否则C在RanF×RanG上不是唯一确定的.反之,若C是一个Copula,F和G是分布函数,则由上式所定义的H(x,y)是一个联合分布函数,其边缘分布函数分别是F和G.
定义 2.2[2]设φ是[0,1]→[0,∞]的连续的、严格单减的凸函数,满足φ(1)=0,φ[-1]:[0,∞]→[0,1]是函数φ的广义逆函数,其定义为
则具有C(u,v)=φ[-1](φ(u)+φ(v))形式的C称为阿基米德Copula,其中函数φ称为阿基米德Copula函数C的生成元.
定义 2.3称函数g(x)为G类函数,如果它满足:
1)g(x)是[0,1]上的递增凹函数(g′(x)≥0,g″(x)≤0)且g(0)=0,g(1)=1;
2) 2g′(x)+xg″(x)≤0,x∈[0,1].
定义 2.4[3]设X、Y是边缘分布分别为F(x)、G(y)的2个随机变量,其联合分布函数为CopulaC(u,v),定义:
若λU,λL∈(0,1],则λU和λL分别为X和Y的上尾相依系数和下尾相依系数,称X和Y上尾相关和下尾相关,若λU,λL=0,称X和Y上尾独立和下尾独立.
3 G类函数的性质
本文是基于G类函数来研究二元Copula函数的构造,因此对G类函数的探究是本文的一个重点.下面给出G类函数的几个相关性质.
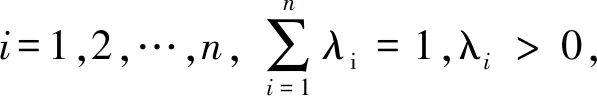

即h(x)在[0,1]上是递增的凹函数,且
所以
仍是G类函数
性质 3.2G类函数的伸缩变换仍是G类函数,即设g1(x)是G类函数,对∀0<α≤1,则
g2(x)=g1(αx)/g1(α)
仍是G类函数.
证明由已知可得g1(x)是G类函数,满足G类函数的所有性质.
即g2(x)在[0,1]上是递增的凹函数,且
g2(0)=g1(0)/g1(α)=0,
g2(1)=g1(α·1)/g1(α)=1.
因为0<α≤1,0≤αx≤1,所以
于是
则
g2(x)=g1(αx)/g1(α)
仍是G类函数.
性质 3.3G类函数的任意复合仍是G类函数.下面只针对二维情况进行说明.
设g1(x)和g2(x)是G类函数,则g(x)=g2(g1(x))仍是G类函数.
证明由已知可得g1(x)、g2(x)是G类函数,满足G类函数的所有性质.
即g(x)在[0,1]上是递增凹函数,且
g(0)=g2(g1(0))=0,
g(1)=g2(g1(1))=1.
因为g1(x)是G类函数,所以
又g2(x)是G类函数,所以
所以
2g′(x)+xg″(x)≤0,
则g(x)=g2(g1(x))仍是G类函数.
4 G类函数的构造方法
二元Copula的构造方法是建立在本文定义的G类函数的基础上,G类函数的寻找是该方法的关键,下面给出一种G类函数的构造方法.
由定义2.3,G类函数必须满足如下2个条件:
1)g(x)是[0,1]上的递增凹函数(g′(x)≥0,g″(x)≤0)且g(0)=0,g(1)=1;
2) 2g′(x)+xg″(x)≤0,x∈[0,1].
下面从条件2)出发,进一步构造满足以上条件的函数g(x).
对于条件2),2g′(x)+xg″(x)≤0,x∈[0,1],令
2y′+xy″=a(x),
a(x)≤0,x∈[0,1],
(*)
对应的齐次线性微分方程是
2y′+xy″=0,
解得齐次方程的2个特解为:y1=1/x,y2=1.故(*)式的通解为
代入(*)式得
补充条件
联立解方程组
得
其中γ1、γ2均为常数,故g(x)的通解为
其中
γ1、γ2均为常数.
下面给出一些G类函数的具体例子和推广.
由上知,只需找到在[0,1]上小于或等于0的函数a(x),进而由(*)式的通解可解得G类函数g(x),从而可构造相应的二元Copula函数.
1)a(x)=βxα,x∈[0,1],其中α和β为参数且α≥0,β<0.
此时a(x)≤0,满足条件,代入上式可得
由初值条件
有
则
因为
所以
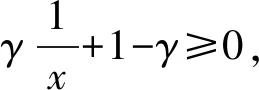
因此
2)a(x)=ωsinx,x∈[0,1],其中ω为参数且ω<0.
此时a(x)≤0,满足条件,代入上式可得
由初值条件
g(1)=-ωsin 1+γ1+γ2=1,
有
γ1+γ2=1+ωsin 1,
则
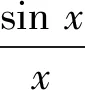
显然γ≥0即可.因此
事实上,凡是满足在[0,1]上小于等于0的函数都可作为a(x),进而按照上述构造方法可以得到无数个G类函数.Copula函数是把随机变量的边际分布连接成联合分布的函数,为变量之间相依结构的分析带来了很大方便,在实际中得到了广泛的应用,尤其Copula函数在金融领域被广泛运用.要更好地分析金融市场,必须首先得到较为精确的Copula函数[4],对Copula构造研究尤为重要.本文基于G类函数对构造二元Copula函数展开研究,下面着重讨论二元Copula函数的新的构造方法.
5 基于G类函数的二元Copula函数的构造
Copula函数在变量之间相关性分析[5]及金融风险管理[6]等方面有广泛的应用,一直以来,构造Copula函数都是人们研究的一个重要课题.本文基于G类函数提出了2种构造二元Copula函数的新方法.
定理 5.1(二元Copula的构造) 设g(x)是G类函数,则
C(u,v)=uvg(u)+ug(v)-ug(u)g(v),
(a)
或
C(u,v)=uvg(u)+ug(v)-ug(uv)
(b)
均是二元Copula函数.称具有这2种形式的Copula为G-Copula,其中函数g称为G-Copula函数C的生成元.
证明下面从二元Copula函数的定义出发,分别证明(a)和(b)式所定义的函数是二元Copula函数.
先证明(a)式所定义的函数
C(u,v)=uvg(u)+ug(v)-ug(u)g(v)
是二元Copula函数.
首先,因为g(x)是G类函数,所以g(x)满足G类函数的所有性质.
1) 边界条件:
C(u,0)=u·0·g(u)+
ug(0)-ug(u)g(0)=0,
C(0,v)=0·v·g(0)+0·g(v)-
0·g(0)g(v)=0,
C(u,1)=ug(u)+ug(1)-ug(u)g(1)=
ug(u)+u-ug(u)=u,
C(1,v)=1·vg(1)+1·g(v)-g(1)g(v)=
v+g(v)-g(v)=v.
2) 2-增性:∀u1≤u2,u1,u2,v1,v2∈I有
VC([u1,u2]×[v1,v2])=
C(u2,v2)-C(u2,v1)-C(u1,v2)+C(u1,v1)=
(v2-v1)(u2g(u2)-u1g(u1))+
(g(v2)-g(v1))+[u1(g(u1)-u1)-
(u2g(u2)-u2)].
因为g(x)在[0,1]上递增的,对∀u1≤u2,v1≤v2有
(v2-v1)(u2g(u2)-u1g(u1))≥0,
g(v2)-g(v1)≥0.
令
w=(u1g(u1)-u1)-
(u2g(u2)-u2),
h(x)=xg(x)-x,x∈[0,1],
则
w=h(u1)-h(u2),
h′(x)=g(x)+xg′(x)-1,
h″(x)=2g′(x)+xg″(x).
由条件
2g′(x)+xg″(x)≤0,x∈[0,1],
可知h″(x)≤0,则h′(x)在[0,1]上是单调递减的,有h′(x)≤h′(0)=-1<0,所以h(x)在[0,1]上是单调递减的.由u1≤u2有
ω=h(u1)-h(u2)≥0,
则对∀u1≤u2,∀v1≤v2,u1,u2,v1,v2∈I有
VC([u1,u2]×[v1,v2])≥0,
所以C(u,v)是2-增的.
综上所述,函数
C(u,v)=uvg(u)+ug(v)-ug(u)g(v)
是二元Copula函数.这就完成了(a)式的证明.
再证明(b)式所定义的函数
C(u,v)=uvg(u)+ug(v)-ug(uv)
是二元Copula函数.
首先,因为g(x)是G类函数,所以g(c)满足G类函数的所有性质.
1) 边界条件:证明同(a)式的证明.
2) 2-增性:∀u1≤u2,u1,u2,v1,v2∈I有
VC([u1,u2]×[v1,v2])=
C(u2,v2)-C(u2,v1)-C(u1,v2)+C(u1,v1)=
(v2-v1)(u2g(u2)-u1g(u1))+
(u2-u1)(g(v2)-g(v1))+u1(g(u1v2)-
g(u1v1))-u2(g(u2v2)-g(u2v1)).
因为g(x)在[0,1]上递增的,对∀u1≤u2,v1≤v2有
(v2-v1)(u2g(u2)-u1g(u1))≥0,
(u2-u1)(g(v2)-g(v1))≥0.
令
w=u1(g(u1v2)-g(u1v1))-
u2(g(u2v2)-g(u2v1)),
h(x)=x(g(xv2)-g(xv1)),x∈[0,1],
则
w=h(u1)-h(u2),
h′(x)=[g(xv2)+xv2g′(xv2)]-
[g(xv1)+xv1g′(xv1)].
又令
u(x,y)=g(xy)+xyg′(xy), ∀x,y∈[0,1],
则
h′(x)=u(x,v2)-u(x,v1),
uy(x,y)=x(2g′(xy)+xyg″(xy)).
由条件
2g′(x)+xg″(x)≤0,x∈[0,1],
可知
2g′(xy)+xyg″(xy)≤0, ∀x,y∈[0,1],
所以
uy(x,y)≤0, ∀x,y∈[0,1],
即对于所有x、u(x,y)关于y是单调递减的.由v1≤v2有
h′(x)=u(x,v2)-u(x,v1)≤0,x∈[0,1],
所以h(x)在[0,1]上是单调递减的,有
w=h(u1)-h(u2)≥0,
则对∀u1≤u2,∀v1≤v2,u1,u2,v1,v2∈I有
VC([u1,u2]×[v1,v2])≥0,
所以C(u,v)是2-增的.
综上所述,函数
C(u,v)=uvg(u)+ug(v)-ug(uv)
是二元Copula函数.这就完成了(b)式的证明.
Copula函数形式多种多样,本文构造的2类二元Copula函数,从形式上看十分简便,由已知的一个G类函数可以得到若干个含参数、不含参数的G类函数,从而得到不同的含参数、非参数的二元Copula函数,扩大了二元Copula函数的范围,丰富了构造二元Copula函数的方法.
6 实证研究
Copula函数作为各变量边缘分布之间的连接函数,可以有效刻画变量间的相关性.本文选取成都市和绵阳市自1985年到2015年期间第一产业产值为研究对象,建立经验分布,并运用常用的阿基米德Copula函数及构造的G-Copula函数和经验Copula函数进行比较,对成都市和绵阳市第一产业产值间的相关性进行分析.在运用Copula函数刻画变量间的相关性时,选择一个合适的Copula函数模型是Copula函数在变量间相关性研究领域中要解决的一个核心问题.首先需要建立变量的经验分布函数.
6.1 经验分布的建立设成都市第一产业产值的增长率为X,绵阳市第一产业产值的增长率为Y,则X、Y是随机变量.我们选取成都市和绵阳市自1985年到2015年历年第一产业生产总值作为样本数据,数据来自统计年鉴,相应的增长率序列分别为{xi,i=1,2,…,30}和{yi,i=1,2,…,30}.对成都市和绵阳市的第一产业产值数据,各选取其中的8个数据作为分割点,把整个数轴分为9段,分别建立其经验分布为
6.2 边缘分布的建立由Sklar定理[7]知,2个随机变量的联合分布是由其各自的边缘分布和对应的Copula函数作用生成,所以需要建立成都市和绵阳市第一产业产值增长率的边缘分布[8].对成都市和绵阳市的历年第一产业产值数据作分析,模拟出两地区产值增长率数据的频率直方图,运用矩法估计各分布的未知参数,计算各分布的理论值和经验分布值的误差平方和,则误差平方和最小值对应的分布为该产值的分布函数.下面首先对成都市第一产业产值增长率和绵阳市第一产业产值增长率进行分析,模拟出两地区产值增长率数据的频率直方图,结果列于图1和图2.
由图1和图2可知,分别采用指数分布Exp(λ)和伽玛分布Ga(θ,μ)去拟合成都市的第一产业产值增长率的总体密度函数,伽玛分布Ga(θ,μ)和卡方分布χ2(n)去拟合绵阳市的第一产业产值增长率的总体密度函数.根据矩法,用样本均值代替总体均值,样本方差代替总体方差,估计出各分布的参数,再选择各分布与相应产值经验分布的误差平方和最小值所对应的分布为X、Y的分布函数.表1给出各产值分布函数的参数估计值及误差平方和.
由表1可知,在用指数分布和伽玛分布拟合成都市第一产业产值增长率的分布时,指数分布与其经验分布的误差平方和最小,因此,选取指数分布模拟成都市第一产业产值的分布,而在用伽玛分布和卡方分布拟合绵阳市第一产业产值增长率的分布时,卡方分布与其经验分布的误差平方和最小,因此,选取卡方分布模拟绵阳市第一产业产值的分布,由此建立了成都市和绵阳市第一产值增长率的边缘分布.
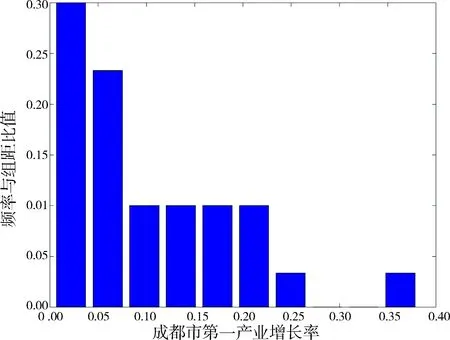
图 1 成都市第一产业产值增长率频率直方图

图 2 绵阳市第一产业产值增长率频率直方图
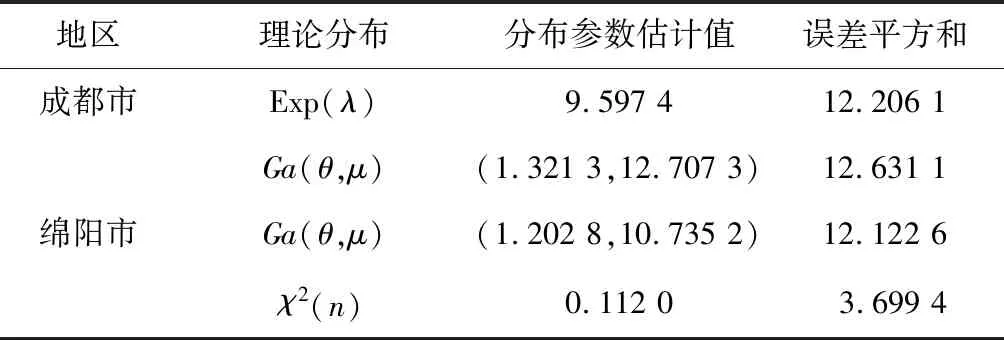
地区理论分布分布参数估计值误差平方和成都市Exp(λ)9.597 412.206 1Ga(θ,μ)(1.321 3,12.707 3)12.631 1绵阳市Ga(θ,μ)(1.202 8,10.735 2)12.122 6χ2(n)0.112 03.699 4
在建立不同地区产值增长率的边缘分布之后,由Sklar定理知,需要选取合适的Copula函数来连接不同地区产值增长率的边缘分布,进而分析不同地区产值的相关关系.而在建立合适的Copula函数模型之前,需要对Copula函数中的参数进行估计.以成都市和绵阳市第一产业产值为例,下面将讨论Copula函数模型中参数的估计.
6.3 Copula函数模型的参数估计在众多的Copula函数族中,阿基米德Copula[9]由于结构简单、构造方便,且具有许多良好的性质而在金融及风险管理等领域得到广泛应用.常用的阿基米德Copula函数有:Frank Copula和Clayton Copula,这2种Copula都能够较好地刻画变量间的相关关系.由于Copula的良好性质[10],对Copula的构造研究[11]显得尤为重要.对这种新的Copula的应用将会是今后的一个研究热点.本文采用Frank Copula、Clayton Copula函数和G-Copula函数来度量成都市和绵阳市第一产业产值之间的相关关系.表2给出了这3类Copula函数的生成元及参数取值范围.
为了得到具体的Copula函数表达形式,需要对Frank Copula、Clayton Copula和G-Copula函数中的未知参数进行估计.由成都市和绵阳市30年的第一产业产值的增长率观测值序列{xi,i=1,2,…,30}和{yi,i=1,2,…,30},可以得到(X,Y)的样本

表 2 3类Copula函数
sign(x)为符号函数

对一般的二元Copula函数,两变量间的总体Kendall秩相关系数τ和Copula函数C(u,v)之间有如下关系[12]

对特殊的Copula函数——阿基米德Copula,两变量间的总体Kendall秩相关系数τ和阿基米德Copula生成元φ(t)之间有如下关系[12]
利用τ与φ(t)间的这种关系,使用Clayton Copula和Frank Copula可以计算出(X,Y)的总体Kendall秩相关系数分别为:
其中

6.4 Copula函数模型的比较在得到Copula函数模型中未知参数的估计值后,需要建立恰当的Copula函数模型.下面对Copula函数进行比较,并寻求最佳的Copula函数.利用成都市和绵阳市第一产业产值增长率序列的经验分布,将增长率序列组合(xi,yi)转化为新的序列(ui,vi),其中
ui=Fn(xi),
vi=Gn(yi),i=1,2,…,n,
n指样本个数.通过比较Copula函数和经验Copula函数之间的偏差平方,对成都市和绵阳市第一产业产值之间的相关性进行分析.首先,计算出第i年的经验分布函数值Cn(ui,vi),其中,i=1,2,…,30,经验分布Cn(u,v)的计算公式为
u,v∈[0,1].
由Copula函数值和经验Copula函数值的偏差平方和
可得到3种Copula函数模拟值和真实值之间的欧氏距离d2,d2越小,则Copula的拟合程度越好.比较3种Copula函数模型,寻求最优的Copula函数,最后度量成都市和绵阳市第一产业产值间的尾部相关,分析不同地区产值间的相关关系.对选取的3种Copula函数进行比较,比较结果如表3.

表3 Copula模型比较结果
从表3检验结果可以看出,对X和Y来说,G-Copula与经验Copula的偏差平方d2为0.011 3,是3个Copula函数中最小的,表示其拟合效果最好,说明在样本区间内G-Copula能够很好地度量成都市第一产业产值和绵阳市第一产业产值之间的相依关系,所以我,选择G-Copula对成都市和绵阳市第一产业产值间的相关性进行度量.
下面用Copula理论来解释尾部相依.根据G-Copula函数表达式,分别计算成都市和绵阳市第一产业产值间的上尾相关系数和下尾相关系数,得到成都市和绵阳市的上尾相关系数λU=0,下尾相关系数λL=0.该结论也与成都市和绵阳市第一产业产值间的散点图中描述的上尾和下尾相关性弱的结论一致,见图3,即成都市和绵阳市的第一产业产值间上尾和下尾都是渐进独立的,没有明显的尾部
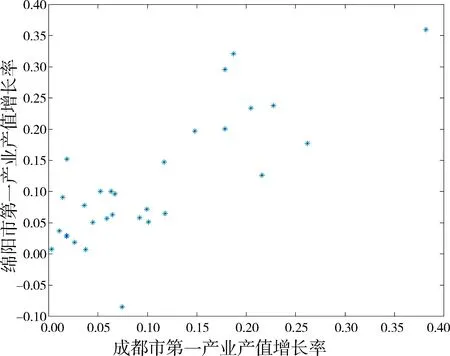
图3 成都市和绵阳市第一产业产值增长率图
相关性.它表明了当成都市和绵阳市其中一个地区产值大幅度增加或减少时,并不会引起另一个地区产值的大幅度增加或减少.因而可知:对于地区产值而言,当一个地区的产值增加或减少到一定幅度时,并不会引起另一个地区产值的大的波动,即通过本文定义的G类函数,找到了一种Copula函数:G-Copula,比常用的阿基米德Copula函数能更好地刻画2个变量之间的相关关系.目前构造二元Copula主要是从函数出发,对函数的性质[14]加以研究,构造出新的Copula[15].基于本文构造的Copula,将它运用到地区产业[16]中,能够较好地分析地区产业的相关关系,有利于实际中对产业经济的研究分析.
7 小结
Copula在刻画变量相关性领域中有广泛的应用.本文提出了一种新的G类函数,基于定义的G类函数,提出了一类新的G-Copula函数,建立了2种构造二元Copula函数的新方法.在构造二元Copula函数时,只需寻找恰当的G类函数,避免了直接从二元Copula函数定义出发去构造二元Copula函数,提高了效率,丰富了构造二元Copula函数的方法.这种新的二元Copula函数扩大了函数模型的选择范围,有利于选择恰当的Copula函数模型来解决实际问题.本文利用构造的Copula函数对成都市第一产业产值和绵阳市第一产业产值之间的相关性进行了实证分析.对于这种新的二元Copula函数在实际中的应用将是以后的研究热点.
