拓展解题方法 提高综合能力

山东

(作者单位：山东省肥城市第一高级中学)

发散求异思维，拓展提升能力

拓展解题方法是提高综合能力的有效措施。平时习题练评过程，不可只追求数量，还要重视质量，要满足“会”做习题，又不要局限于一种解题方法，要善于从不同角度去审视、思考和理解问题，寻求多种解题方法和途径。进行“发散”和“求异”思维训练，是知识内化和提高综合能力的表现，也是培养具有创新意识和创新精神的体现，对于知识系统化，深刻理解和灵活应用都大有裨益。

如图所示，质量为4m的绝缘小车静止在光滑水平地面上，其光滑的上表面放有一质量为m的小滑块，静止时滑块距小车右边的距离为L，滑块带有电荷量为q的正电荷。现加一水平向右的场强为E的匀强电场，欲使带电滑块由静止向右运动，并与小车右边挡板发生碰撞，设碰撞的时间极短，碰撞过程没有动能损失，且滑块的电量保持不变。求：

(1)碰撞后滑块和小车的速度分别为多少？

(2)碰撞后滑块和小车相距的最大距离？

【命题意图】由知识立意向能力立意转化，增大试题思维容量，注重对思维品质的考查。该题为陈题出新，以力学和电学为背景材料的力电综合题，主要考查知识点有相对运动(参考系)、匀速直线运动和匀变速直线运动及公式、v-t图象、电场和电场力、牛顿第二定律、动量定理、动能定理、动量守恒定律、能量守恒定律。

【解析】(1)滑块与小车间无摩擦，滑块向右加速运动L的过程中，小车保持静止状态，设滑块运动到小车右端的速度为v

法1 根据动能定理

法2 根据牛顿第二定律

qE=ma①′

根据运动学公式

v2=2aL②′

法3 根据动量定理

qEt0=mv-0 ③′

根据运动学公式

设碰后的瞬间滑块和小车的速度分别为v1、v2，以滑块和小车为系统，由动量守恒得

mv=mv1+4mv2②

根据能量守恒得

【点评】滑块向右加速运动L的末速度为v，电场力是恒力，三种方法均可以求出滑块向右加速运动的末速度v，当电场力为变力时，显然牛顿第二定律和动量定理不再适用，故此时法1更直接；三种方法的具体选择使用需依据题目条件，应灵活选取，不是一成不变的。

(2)碰撞后滑块与小车以共同速度运动时，滑块与小车右边相距最大距离为sm。

法1 滑块与小车碰后的瞬间，滑块相对小车向左运动的初速度v相1

v相1=v1-(-v2)=v1+v2=v④

滑块与小车达共同速度时，滑块相对小车的速度v相2

v相2=v块-v车=v2-v2=0 ⑤

滑块受向右的电场力向左做匀减速运动，根据动能定理

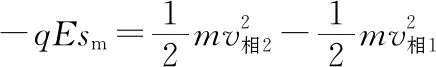
由①④⑤⑥式联解得sm=L

【点评】全程对滑块研究，根据相对运动和运动学公式，动能定理求解，过程简洁，关键在理解，建构模型和寻找滑块与小车碰后初、末状态的相对速度，在列式的过程中关键是明确速度的矢量性，即速度方向的选取问题，本题求解的巧妙之处是参考性的灵活转换，以运动的小车为参考系，使得解题方式更为简洁。

法2 滑块与小车碰后向左减速到零为第一段，设运动时间为t1，两者相距为s1，根据动量定理

-qEt1=0-mv1⑦

根据运动学

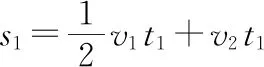
滑块从静止开始向右加速到v2为第二段，设运动时间为t2，滑块与小车再相距为s2，根据动量定理

qEt2=mv2-0 ⑨

根据运动学公式

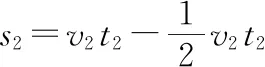
那么sm=s1+s2=L

【点评】本题的解题特点是分段对滑块和小车应用动量定理，结合相对运动和运动学公式求解，关键在理解各段两者的运动特点，构建模型，对系统各段列相对运动方程，特别是注意物理公式的矢量性及s1、s2与sm的数量关系。

法3 滑块碰后先向左减速到零再向右加速到v2，运动时间为t，根据动量定理

qEt=mv2-(-mv1)

在时间t1内，滑块与小车相距为s相1，根据运动学公式

在时间t2内，滑块与小车相距为s相2，根据运动学公式

那么sm=s相1+s相2=L

【点评】法2与法3的解题思路基本类似，但后者与前者相比较，滑块与小车相对运动思路更明晰，它采用的方法更为基本，但需要思路清晰，根据相对运动列出运动方程和。

法4 滑块碰后以v1的速度向左减速到零再向右加速到v2，经历时间为t，设小车在t时间内向右做匀速运动的位移为s车，根据运动学

s车=v2t

滑块在t时间内向左减速运动，设初速度为-v1，末速度为v2，位移为s块，根据动能定理

那么sm=s车+s块=L

【点评】在全过程时间t内，分别以滑块和小车为研究对象，解题思路比法2和法3更清晰简洁，关键在于理解滑块和小车的运动特点，构建模型，对小车列运动位移方程，对滑块列能量方程，结合二者的数量关系联立得出结果，对解题者的能力要求较高。

法5 根据(1)中v1、v2和动能定理求出各段的时间t1、t2，总时间t，作出v-t图象，利用v-t图象与坐标轴所围面积，并根据相对运动的关系，在时间t内滑块和小车相距的最大距离sm等于△ABD的面积S△ABD

【点评】运用图象法解题是高中物理教学的能力培养任务之一，本题可以利用v-t图象与坐标轴所围面积所反映的物理意义，并根据相对运动关系有sm=S△ABD，此法比前四种方法直观简洁，关键是作出v-t图象，确定sm等于v-t图象与坐标轴所围的哪一块面积。此方法抽象度高，能力要求较高，也是高中生重点培养的素养之一。