通过近三年全国卷Ⅰ高考压轴题分析探究物理学科核心素养与建立模型教学

河北 北京

(作者单位：河北省沧州市华北油田第三中学；北京市北京林业大学工学院)

注重在基本题目中建模，在建模中提升推理和综合分析能力

每当提到高考压轴题目时，学生首先想到的就是一个字“难”，因此好多学生不敢触碰压轴计算大题，本文对近三年全国卷Ⅰ的第25题进行分析，通过拆解运动过程，突显各个模型的建立，把复杂问题简单化呈现，让学生能够在复杂的内容设计中寻到自己的得分点，克服畏难情感。

【原题再现】

【2019年卷Ⅰ25题】竖直面内一倾斜轨道与一足够长的水平轨道通过一小段光滑圆弧平滑连接，小物块B静止于水平轨道的最左端，如图(a)所示。t=0时刻，小物块A在倾斜轨道上从静止开始下滑，一段时间后与B发生弹性碰撞(碰撞时间极短)；当A返回到倾斜轨道上的P点(图中未标出)时，速度减为0，此时对其施加一外力，使其在倾斜轨道上保持静止。物块A运动的v-t图象如图(b)所示，图中的v1和t1均为未知量。已知A的质量为m，初始时A与B的高度差为H，重力加速度大小为g，不计空气阻力。

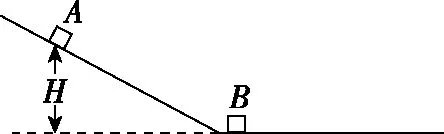
图(a)

图(b)

(1)求物块B的质量；

(2)在图(b)所描述的整个运动过程中，求物块A克服摩擦力所做的功；

(3)已知两物块与轨道间的动摩擦因数均相等，在物块B停止运动后，改变物块与轨道间的动摩擦因数，然后将A从P点释放，一段时间后A刚好能与B再次碰上。求改变前后动摩擦因数的比值。

【分析】解题时对于运动过程，我们需要从初始条件开始，按照程序清晰呈现每一个运动过程的分运动，然后根据运动模型写出对应的物理表达式。现在我们按照过程逐一展开分析。

模型一、完全弹性碰撞：物块A和物块B发生碰撞瞬间的速度分别为vA、vB，弹性碰撞过程满足动量守恒和机械能守恒，即mv1=mvA+mBvB

解得mB=3m，第一问求解完毕。这是很常规的一道小计算问题，同学们应该不会感觉到压力。

模型二、牛顿第二定律：设斜面的倾角为θ

当物块A沿斜面下滑时mgsinθ-f=ma1

当物体A沿斜面上滑时mgsinθ+f=ma2

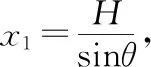
模型四、功的定义：故物块A在描述的整个过程中，克服摩擦力做的总功为

第二问解答完毕。这一问中涉及的模型稍微多一点，但也没有生、新模型，均为传统的常规题型，得分率应该不会太低。需要注意的是遇到多过程多模型问题，一定要细心，按照程序法逐一攻破。下面开始分析第三问。

模型五、系统总能量守恒(难度有些大)。以A和B组成的系统，因为碰撞过程中满足完全弹性碰撞，所以研究的过程从A开始下滑到碰后A滑到最高点以及B停下的全过程。

设物块B在水平面上最远的滑行距离为s，设原来的动摩擦因数为μ，根据前面求解知道

根据能量守恒定律有A减少的重力势能全部用来克服摩擦力做功而转化为了内能，即有

模型六、恰好碰上模型(“恰好”模型之一)：此条件可解读为将A从P点释放，A恰好能与B再次碰上，即A恰好滑到物块B位置时，速度减为零。设改变后的动摩擦因数为μ′，然后以A为研究对象，根据能量守恒定律得

本题这样一拆解运动过程，通过过程嫁接对应的解题模型，我们不难发现每一个过程都变成了学生们已掌握知识清单中的常练模型。至此本题便可迎刃而解。实际上模型五如果不习惯用系统总能量守恒模型，完全可以用耳熟能详的动能定理取代。用同样的方法我们再来分析一下2018年的高考压轴题目。

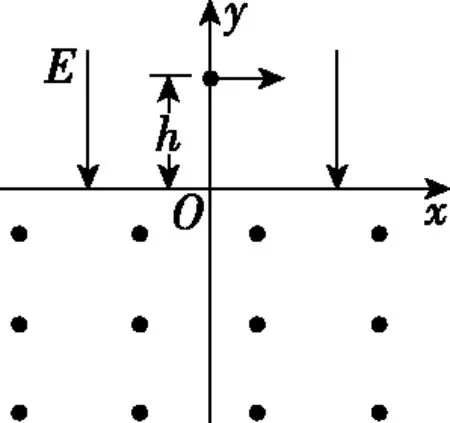
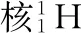
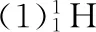
(2)磁场的磁感应强度大小；

解析本题涉及的模型：

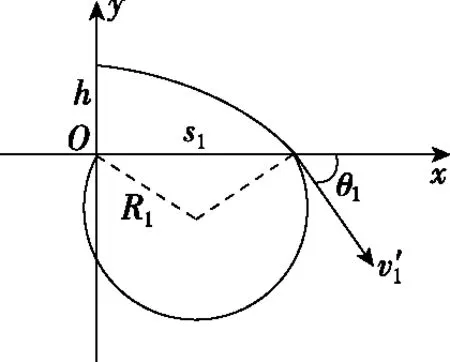
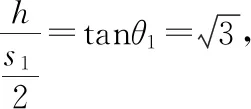
这种方法更为简单，但需要学生对这个模型熟练应用。

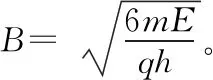
但是在第三问中没有新的模型与第二问相似，就不再重复了。

【2017年卷Ⅰ25题】真空中存在电场强度大小为E1的匀强电场，一带电油滴在该电场中竖直向上做匀速直线运动，速度大小为v0，在油滴处于位置A时，将电场强度的大小突然增大到某值，但保持其方向不变。持续一段时间t1后，又突然将电场反向，但保持其大小不变；再持续同样一段时间后，油滴运动到B点。重力加速度大小为g。

(1)求油滴运动到B点时的速度；

(2)求增大后的电场强度的大小；为保证后来的电场强度比原来的大，试给出相应的t1和v0应满足的条件。已知不存在电场时，油滴以初速度v0做竖直上抛运动的最大高度恰好等于B、A两点间距离的两倍。

解析本题看似很难，实际也是几个模型的堆积：

模型一、匀速直线运动：合外力为零。因为是带电油滴，所以重力等于电场力，且电场力方向向上，即mg=qE1。这一步多数学生能解决，但是看过后面的条件思路就开始混乱，越读越没底气，以至于第一个二力平衡的式子都写不出了。

模型二、牛顿第二定律——匀变速直线运动：第一个是匀加速直线运动，qE2-mg=ma1，v1=v0+a1t1，第二个是匀减速直线运动，qE2+mg=ma2，v2=v1-a2t1，联立几式即得v2=v0-2gt1。题目中电场时而向上，时而向下，某些学生思路就开始乱了。其实坚定解题思路，果断列出公式，这才是解题的正确思维。

这三个模型并没有特别深奥之处，且均是我们常规做题时遇见的。为什么在高考最后一题中出现，那么多学生得不到相应的分数，就是因为给它冠以压轴题的标签。

本题进行第二问的求解过程中，真正的障碍不是前面基本模型，而是第四个模型。

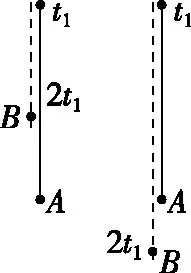
模型四、运动情形示意图，如图中的两种情形。有了这个运动模型再加上相应的数学推导，就能完美解出最后的答案了(此处省略数学推导)，完整写完这道题的考生真的是凤毛麟角，这也是高考选拔的特性。

实际上我们在教学中就应该体现这种模型建立的教学法。凡是遇到过程稍多的所谓难题，我们解题硬功夫就是庖丁解牛，肢解各个模型。

模型的建立要从根基做起，充分利用课本，从最简单的问题归纳总结核心知识，充分发挥老师的课堂驾驭功底，把功课做到每一节课堂。针对课本每一节的练习和例题，我们要引领学生挖掘教材中研究这道题的目的，意在告诉我们什么样的信息，我们从中可以提炼出什么样的模型。

如人教版选修3-1闭合电路欧姆定律一节的例题：如图所示，R1=14 Ω，R2=9 Ω。当开关处于位置1时，电流表读数I1=0.2 A；当开关处于位置2时，电流表读数I2=0.3 A。求电源的电动势E和内阻r。

这道题目放在课堂中要求学生绝对不只是列出两个方程联立解出E和r的数值。

针对物理学科特点，本着物理育人的宗旨，让学生深度思考、讨论总结出测量电源电动势和内阻的三种方法。借此总结解决此类问题的主旨，即测量电源电动势和内阻的三种基本模型：电流电阻法、电压电阻法、电压电流法。从课堂教学中培养学生的概括总结能力，贯彻物理核心素养教学目标。

而高三复习中我们应该从课本中跳出来，模型也需综合，比如概念模型、运动模型、解题方法模型、二级结论模型等。模型形式较广，并不是只有定理、定义、概念、结论，还包括题中条件对应的解题模型。比如在天体一章中，有这样的题目：

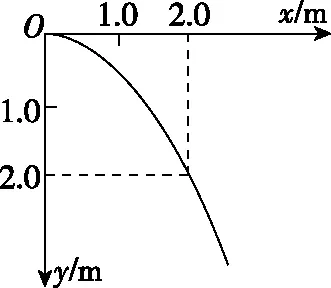
宇航员在某星球表面以初速度2.0 m/s水平抛出一物体，并记录下物体的运动轨迹，如图所示，O点为抛出点，若该星球半径为4 000 km，万有引力常量G=6.67×10-22N·m2·kg-2。则下列说法正确的是

( )

A.该星球表面的重力加速度4.0 m/s2

B.该星球的质量为2.4×1023kg

C.该星球的第一宇宙速度为4.0 km/s

D.若发射一颗该星球的同步卫星，则同步卫星的绕行速度一定大于4.0 km/s

这道题目应引导学生建立这样的模型：以初速度2.0 m/s 水平抛出后做平抛运动是已知条件，目的是要求出物体运动时的加速度，即星球表面的重力加速度。随后总结类似的条件有自由落体运动、竖直上抛运动、平抛运动、斜抛运动、单摆周期、圆周运动最高和最低点的向心力等，根据这些条件对应求星球表面重力加速度的模型。

老师不仅引导学生总结模型，还要训练学生如何使用模型解题。每一个模型都有对应的前提条件，比如我们见到匀速直线运动和静止状态就直接应用力的平衡方程列式求解，这实际上就是模型应用的解题方法。学生们见到碰撞就知道应用动量守恒定律，老师还应该帮助同学们归纳哪些情况下还可以应用动量守恒定律。从本质上来讲动量守恒定律的条件是系统所受合外力为零，这才是应用动量守恒定律的根本，在题目条件中我们要深挖是否有物体系作为研究对象，物体系所受外力是否为零。讲解题目时不要把重点放在列方程中，而是要重点分析题目中从哪些已知量或关键字中找到符合对应模型的条件。让学生们慢慢掌握如何读题、审题，以及识别一类题的解决方法，真正从中领悟条件和模型的对应关系，发挥应用模型解题的便捷，从题海中跳出来，驾驭高中物理概念、体会物理思维方法，提升发现问题、解决问题的综合素养。