核心素养模式下的高三一轮复习——以“匀变速直线运动”为例

广东

(作者单位：广东省汕尾市海丰县彭湃中学)

变中生智，错中悟理

高三一轮复习对于学生物理知识体系的形成、学科思维的发展和学科能力的提高起着重要作用。但现实中学生以做题代替复习，深陷题海疲惫不堪，老师讲解得面面俱到但又一带而过，复习效果不尽如人意。笔者结合教学实际，以匀变速直线运动的复习为例，通过精选例题，利用一题多解、一题多变、巧用错解等策略破解上述困境，取得了较好的效果。

匀变速直线运动是高中阶段学习的主要运动模型之一，是历年高考考查的核心考点，可以以选择、计算、实验多种题型考查。考纲对匀变速直线运动及其公式、图象的要求为Ⅱ级要求，即“能够理解公式、图象的确切含义及其与其他知识的联系，并能在实际问题的分析、综合、推理和判断等过程中进行运用”。

一、构建知识网图，完善物理观念

在一轮复习时，首先引导学生构建图1所示的知识网状图。通过多媒体呈现图1的主体框架(隐藏了关键的知识点)，以该框架为基础，引导学生回顾匀变速直线运动的相关知识点并完善知识网图。

图1

上述教学过程中，通过v-t图象对判别式、比例式进行简单的推导，目的有二：①匀变速直线运动的基本规律学生平时应用较多，相对比较熟悉，但推论和比例式学生应用较少，对式中物理量的物理意义理解不透彻，导致在具体问题中无法快速、准确地选择合适的方法，而推导的过程就是学生再理解的过程，有利于学生对相关知识的掌握。②选择利用v-t图象进行推导，一是省时，二是直观，同时也有利于学生掌握v-t图象面积的物理意义。

二、精心筛选例题，培养科学思维

高三教学中习题教学所占比例很大，对于科学思维的培养应在习题上下工夫。在梳理匀变速直线运动相关知识点的基础上，通过一题多解、一题多变等教学方法，在遵循学生思维规律的基础上，因势利导，将一个问题从不同角度进行设问与思考，培养学生的发散思维和创造性思维能力。

1.一题多解，发展学科思维

匀变速直线运动的规律、推论及比例式较多，面对具体的物理问题，学生常常无法在众多公式中选取合适的物理规律进行求解。而一题多解教学，可根据学生自身学习实际找到一种解题方法，通过知识的牵引，得到更多解题方法，使学生能够融会贯通，树立学习物理的自信心，同时帮助学生理顺物理知识网络，建构知识体系，发展学科思维，提高课堂效率。

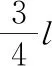
图2

解题的过程是学生思维转换的过程，首先需要将物理问题转换成相应的物理模型，然后根据已知信息和所求信息，结合所学物理规律，寻找合适的解题方法。学生看到例1 后能够快速判断出小球做匀减速直线运动，并发现题目所给信息和所求信息均与位移、时间有关，从而产生了解法1。

【解法1】基本运动规律

设小球初速度为vA，从B到C的时间为tBC。由位移公式可得

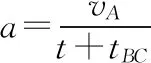
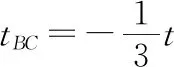
在理解匀变速直线运动规律的基础上学生能够准确书写方程，但联立方程求解时发现解题过程太过繁琐，不能在短时间内得到最终结果。面对解法1的弊端，引导学生思考：能不能求出小球经过B点时的速度呢？

【解法2】中间时刻速度公式

设小球经过B点时的速度为vB，由速度位移公式可得

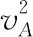
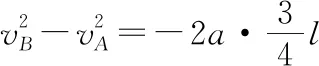
故tBC=t

该方法对学生思维要求较低，运算量较小，能够促使学生准确理解、运用匀变速直线运动中间时刻速度公式和平均速度公式，对于基础相对薄弱的学生比较适用。

【解法3】逆向思维

A到C的过程为末速度为零的匀减速直线运动，则C到A的过程为初速度为零的匀加速直线运动，由位移公式得

联立⑥⑦解得tBC=t

该方法数学运算量较小，但对思维要求较高，对于基础较好的学生比较适宜。

【解法4】比例关系求解

对于初速度为零的匀变速直线运动，物体在连续相等时间内通过的位移满足

x1∶x2∶x3∶…∶xn=1∶3∶5∶…∶(2n-1)

故tBC=t

该方法是在逆向思维的基础上运用初速度为零的匀加速直线运动的比例式进行求解，有助于学生对该比例式的准确理解、运用。

四种解法解答过程由繁到简，但对学生的物理思维要求逐渐提高。该题的讲解不仅可以促使学生对匀变速直线运动的基本规律、推论、比例式等内容形成完整的知识体系，加深对物理规律的理解，也有助于培养、发展学生的学科思维，使学生受益终身。

2.一题多变，提高学科能力

物理图象是对事实进行解释的重要形式，2019年高考物理试题的一大特色就是突出图象的呈现方式，考查学生的信息加工能力。运动学图象问题一直是高考考查的热点，主要以x-t图象和v-t图象为主。在图象的复习中通过一题多变，使学生全面深入地理解图象的物理意义，提高学生的学科能力。

【例2】(2014年天津卷)质点做直线运动的速度—时间图象如图3所示，该质点

( )

图3

A.在第1秒末速度方向发生了改变

B.在第2秒末加速度方向发生了改变

C.在前2秒内发生的位移为零

D.第3秒末和第5秒末的位置相同

【解析】本题主要考查v-t图象的斜率及图线与坐标轴所围面积的物理意义，正确答案为D。

【变式1】请画出例2中v-t图象对应的x-t图象和a-t图象。

变式1提出后，大多数学生都能正确绘制a-t图象(如图4)，但在绘制x-t图象时，学生基本上都只关注位移的大小变化，通过计算1 s末、2 s末等时刻位移的大小描点连线得到图5所示的图象。

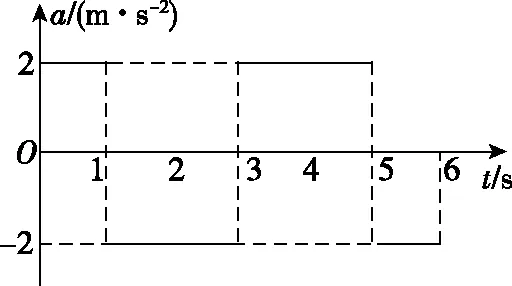
图4

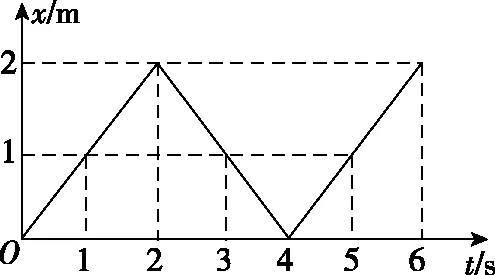
图5

师：图3所描述的质点运动过程中，速度如何变化？

生：先增大，1 s末开始减小，2 s末开始又反向增大……

师：x-t图象的斜率表示什么？

生：速度。

师：大家看看自己所绘制的x-t图象对应的速度如何变化？

通过上述对话，学生意识到自己在绘制x-t图象时忽视了速度的变化，对自己所绘图象进行修改，得到正确答案(如图6)。

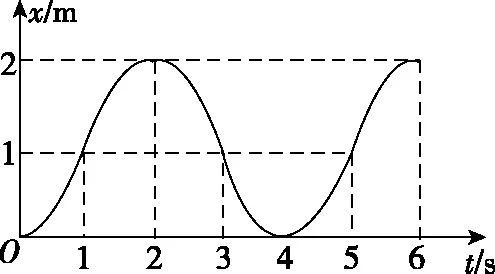
图6

【变式2】质点做直线运动的v-t图象如图7所示，关于该过程的描述正确的是

( )

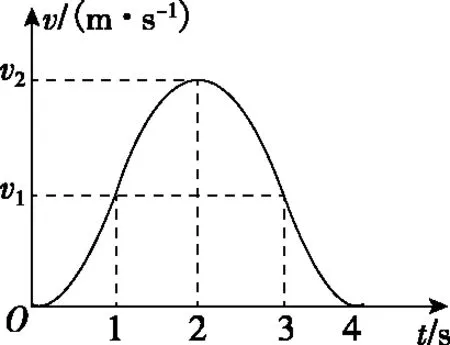
图7

A.4秒末质点回到出发点

C.前2秒内位移和后2秒内位移大小相等

D.质点加速度先增大后减小

变式2是在图6的基础上将x-t图象变为v-t图象。学生能够快速判断AD错误，根据对称的关系得到C正确，但对于B选项的判断出现了困难。

师：若第2秒内质点作匀变速直线运动速度从v1变到v2，其图线如何？

生：一条直线。

师：(画出图线，如图8)该直线所描述的运动在第2秒内的平均速度多大？

图8

师：第2秒内直线和曲线哪条图线与坐标轴所围面积大？

生：曲线围成的面积大。

【变式3】质点做直线运动的a-t图象如图9所示，关于该过程的描述正确的是

( )

图9

A.4秒内加速度恒定

B.第1秒内质点做加速运动，第2秒内质点做减速运动

C.前3秒速度变化量为6 m/s

D.前3秒速度变化量为-2 m/s

变式3是对运动学图象的拓展，正确答案为D。AB两个选项学生比较容易理解，但对CD两个选项的判断比较困难。教学时从v-t图象面积的物理意义出发，运用类比的方法结合微积分的思想，使学生理解a-t图象的图线与坐标轴所围图形的面积表示速度变化量(时间轴上方为正，时间轴下方为负，且正负表示方向)。同时引导学生思考F-s、F-t、I-t等图象图线与坐标轴所围图象面积的物理意义，既能为后续的复习做好铺垫，也可以提高学生的迁移创新能力。

3.巧用错解，理解物理模型

学生在解题的过程中经常会犯一些错误，根据2018届和2019届学生常犯的错误，笔者选择顺应学生的思维习惯，通过例3引导学生发现解题错误的原因，理解物理模型和生活现象之间的区别与联系。

【例3】如图10所示，A、B两物体(可视为质点)相距x=7 m，物体A以vA=4 m/s的速度向右匀速运动，而物体B此时的速度vB=10 m/s，只在摩擦力作用下向右做匀减速运动，加速度为a=-2 m/s2，那么物体A追上物体B所用的时间为

( )

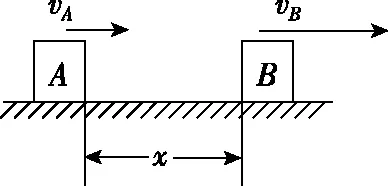
图10

A.7 s B.8 s C.9 s D.10 s

【错解】设经过时间t物体A追上物体B，其位置关系如图11。则有xA=xB+x⑧

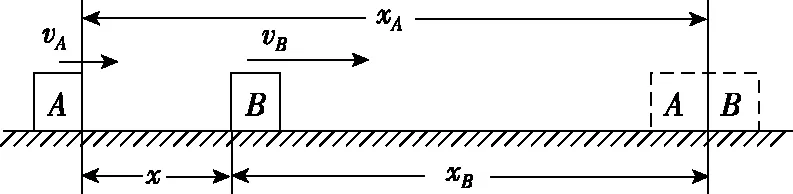
图11

又xA=vAt⑨

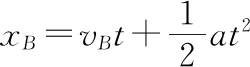
联立⑧⑨⑩解得t=7 s或t=-1 s(舍去)

师：请大家检查上述解题过程有没有问题？

(个别学生开始讨论……)

师：物体B经过多长时间速度减小为0？

生：经过5 s。

师：5 s后物体B保持静止还是反向加速？

生：保持静止。

学生恍然大悟，经过计算发现物体A需经过8 s才能追上物体B。进一步引导学生总结：若B在减速阶段被追上，则A、B运动时间相同；若B在静止后被追上，则A运动的时间大于B运动的时间。今后在处理类似问题时应先做必要的判断。

上述错解的原因从表面上看是学生审题不够仔细，但从本质上分析则是学生对物理模型与生活现象的区别及联系理解不准确。物理模型是对生活现象的抽象概括，解题时首先要将物理问题转换为相应的物理模型，但应用物理模型解决具体物理问题时还需要结合实际考虑物理问题与物理模型的融洽性。例3中物体B的运动其实就是生活中的刹车现象，而匀减速直线运动是理想化的运动模型，二者的关系如图12，可见刹车现象与之对应的物理模型不是完全融洽的。

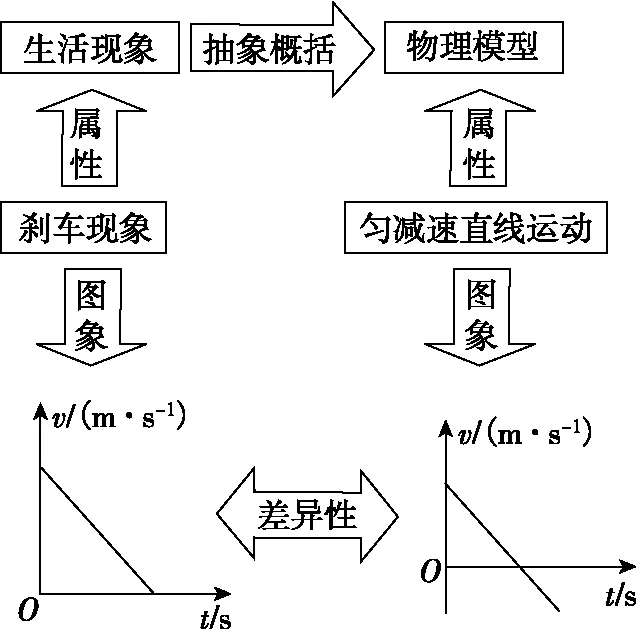
图12

三、适量练习，巩固课堂成效