五个关注——让数学课堂练习更加有效

陈瑞辉

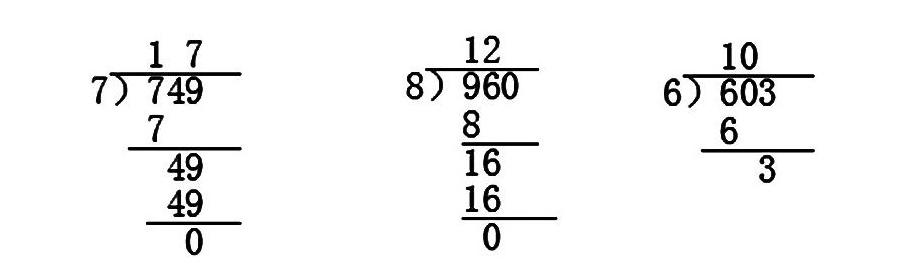
[摘 要]

從关注教学内容的本身;关注学生的认知规律;关注学生的年龄特点;关注学生的生活实际;关注知识的发展延伸等五个方面，探讨了数学课堂练习的有效性，提高课堂教学质量，发展学生的认知、思维、技能及数学素养。

[关键词]

小学数学;课堂练习;有效性

课堂练习是学生掌握知识，发展智能，形成素养的重要手段。数学课堂练习设计的优劣，直接影响着课堂教育教学质量，关系到学生认知、思维、技能及素养的发展。然而，当今课堂教学中，还存在着部分教师在练习的设计上过分追求舍本逐末，缺失课堂练习的本真，脱离数学本质;有些则形式单一、机械重复，导致学生学习乏味，练习作用不高，效果不佳，这些都是不可取的。笔者认为，数学课堂练习的组织与实施，既要能真正起到巩固内化、交流反馈和发展延伸的作用，又要尽可能让所有学生都能主动参与，通过练习来实现掌握所学知识，激发积极情感，丰富数学体验，积累活动经验，提高思维水平。有效的数学课堂练习应着重关注以下五个方面。

一、关注教学内容的本身——练习内容要有针对性

课堂练习首先应有目的、有步骤地进行，促进学生掌握知识，发展技能、提升素养。首先教师应吃透教材，把握好教学的目标、重难点及其关键，对练习意图要有一个明确、整体的把握，即巩固哪些知识，形成哪些技能，发展哪些核心素养？应有针对性地组织练习活动。

（一）“依”目标练习

教学目标是教师“教”和学生“学”的依据与导向，练习要“依”目标来展开。譬如：（1）辅垫性练习。辅垫练习是课堂教学的前奏，是新旧知识之间的“桥梁”。为使新旧知识更好地衔接起来，突出知识前后的内在联系，在备课时应精心设计，为学习的迁移创设条件。

例如，教学《同分母分数加减法》一课，可这样设计铺垫练习：（1）说一说[35]、[67]、[223]分数单位分别是多少。（2）[28]+[58]=（  ），想：（  ）个[（）（）]加（  ）个[（）（）]是（  ）个[（）（）]，也就是[（）（）];[79]-[49]=（  ），想：（  ）个[（）（）]减（  ）个[（）（）]是（  ）个[（）（）]，也就是[（）（）]。这样一练，学生对同分母分数加减法算理的理解以及算法的总结便茅塞顿开，水到渠成。（2）形成性练习。教学完乘除法之间关系时，可这样组织练习：根据26×18=468，直接说出468÷18=________，392÷26=________，并让学生说出解题根据。还可让学生说出填空题（  ）中的数的求法，如（  ）×13=390，75×（  ）=450等。

（二）“扣”重点练习

抓住数学本质，将抽象的数学知识具象化，是突破教学重点有效策略之一。例如，《分数的意义》一课的重点在于让学生能正确理解分数的意义。教学时笔者设计了这样的一道题;用分数表示下面图中阴影部分的面积。

并提问：上面的长方形完全一样，平均分的方法一样吗？每一份的面积一样吗？为什么？通过这样练习使学生对分数意义的理解从感性上升到理性，形成“质”的飞跃。

（三）“把”关键练习

每个知识点，都有解题关键，把握住关键，也就找到解题的“金钥匙”。在用方程解决问题中，根据题目中的数量关系，找出等量关系列方程式是解题关键。例如：小青买2节五号电池，付出6元，找回0.4元，每节五号电池的价钱是多少元？在学生掌握一般思路（付出的钱数-2节电池的钱数=找回的钱数，即：6元-2X=0.4元的基础上，教师进一步挖掘题目内涵，让学生找出题目中隐含的其他等量关系：（1）2节电池的价钱+找回的钱数=付出的钱数，即2X+0.4=6元;（2）2节电池的钱数=付出的钱数-找回的钱数，即：2X=6-0.4（3）（付出的钱数-找回的钱数）÷每节电池钱数=买电池节数，即（6-0.4）÷X=2;……这样训练不仅让学生抓住了解题关键，而且提高了思维的发散性和灵敏性。

（四）“破”难点练习

讲方法有针对性地突破教学难点，可以提高学生学好数学的自信心，还可以减轻学生的学习负担，同时也能更有效达成教学目标。例如，教学《商中间有0的除法》和《商末尾有0的除法》这两课时，“除到被除数的哪一位不够商1，上商0”是本课教学的难点，练习时我们可设计学生在计算中经常出现的“顽症”，让“小医生”来治一治：

这样练习能使学生吃堑长智，避免重蹈覆辙，即突破了难点，又掌握了新知。

二、关注学生的认知规律——练习过程注重层次性

学生的认识规律总是由浅入深，由易到难，练习设计应循序渐进，逐步提高，有层次、有梯度。面向全体学生，着眼中等生，配好必会练习和自选练习，既给后进生辅导性练习，又给优秀生提高性练习。

以一般应用题为例，可设计这样练习：一个修路队原计划每天修路1.35千米，12天可修完，

_____________________________________________________________

（1）实际10天修完，每天修多少千米？

（2）实际10天修完，每天多修多少千米？

（3）实际提前2天修完，每天修多少千米？

（4）实际提前2天修完，每天多修多少千米？（自选题）

（5）实际每天多修0.27千米，可提前几天修完？（自选题）

……

这样练习依标扣本，立足中等生，兼顾两头，让不同的学生在数学上得到不同的发展，符合素质教育学生发展的要求。

三、关注学生的年龄特点——练习形式力求灵巧性

苏霍姆林斯基说过：“学习兴趣是学习活动的动力。”练习形式应采取灵巧多样，激起学生的浓厚兴趣。如概念教学方面的练习可采用填空题、选择题、判断题、匹配题等;解决问题教学方面的练习可采用补充条件、补充问题、对比题、改编题、一题多解、一题多变等;图形与几何方面教学的练习可用量一量、画一画、拼一拼、折一折等实践操作练习。练习形式上可根据不同年级学生的年龄特点，灵活地采用做游戏、讲故事、“开火车”、数学寻“宝”、“小动物找家”、数学闯关等来激发学生的学习兴趣，通过类此灵活巧妙的练习，不但内化数学新识，增长智慧，发展思维，而且能激发学生强烈的学习热情，体验数学学习的无穷乐趣。

例如，教学《三角形的特性》一課，练习环节我带领孩子们走进“动物乐园”玩起了游戏：

多媒体动画播放：

聪明兔：我身后图形露出的一个角是直角，小朋友，你们猜，它可能是什么图形呢？

生：（一致认为）直角三角形。

（结果小兔抽出的是长方形或正方形或其他的一些不规则图形）

师：啊？为什么猜错了呢？（生顿悟：原来小兔没有告诉大家它身后藏着的一定是三角形）现在老师告诉大家，其他小动物身后藏着的都是三角形。

伶俐猫：我身后图形露出的是一个钝角，亲爱的小朋友，你们猜，它是什么图形呢？

智慧狮：我身后的三角形露出的一个直角，大家猜，它是什么三角形呢？

机灵猴：我身后的三角形露出了一个锐角，聪明的小朋友，你们猜，它是什么三角形呢？（注重让学生感悟和理解：锐角、直角、钝角三类三角形均有可能）

四、关注学生的生活实际——练习题材讲究新颖性

练习题材应以生活为“胚胎”，既要做到联系实际、不落俗套，又要实而不偏，典型新颖。使数学学习与学生生活实际紧密结合，感悟数学的应用与奇妙，激发学生学以致用的意识，培养解决问题的能力。例如，教学《百分数的应用》时，设计了这样的两组题：

（一）购物中的学问（互动解答）

师：前些天陈老师在逛商场时，遇到了这样的一件事：同样的一套服装，SM城市广场打八折出售;而莱雅百货则打出了“迎五一，七折优惠大酬宾”的牌子，你们猜，陈老师会上哪家商店买呢？

（生大多数：肯定上莱雅百货买，因为它打七折，更便宜。少部分学生反驳：我觉得不一定，还得看原标价。）

师：SM城市广场这套西服的标价是1000元，打八折是800元;而莱雅百货的标价是1300元;打七折是910元，你们说老师会上哪家商店买呢？

（生顿悟、齐答：上SM城市广场买。）

师（开心地）：节省110元钱还够老师美美的吃上一顿“肯德基”呢！这个原标价，就是我们学过的百分数问题中的什么量？（单位“1”的量）可见，单位“1”的量对我们解答百分数问题非常重要。……

（二）信息背后的信息（阅读解答）

厦门市旅发委近日在官网“晒”出2018年度成绩单：

2018年厦门市共接待国内外游客8900.32万人次，同比增长13.66%;旅游总收入1402.12亿元人民币，同比增长19.99%。……随着厦门地铁的建设、旅游环境的提升以及国家主导的“体验经济”“产业链经济”时代的来临，国民消费和出行水平迅速提升，预计今年来厦旅游观光的游客同比还将增长两成，厦门的经济发展后劲也将越来越强劲。（摘自闽南网）

根据以上信息你还能知道其他的一些相关信息吗？使学生在读读算算过程中，感受到祖国和家乡旅游事业取得的辉煌成就，受到爱祖国、爱家乡的教育。

五、关注知识的发展延伸——综合拓展形成系统性

要使学生比较全面、系统地掌握某一方面的知识，在练习设计上就必然要考虑对新知合理的综合与延伸，巧妙沟通新旧知识间的内在联系，以及发展脉络。通过综合拓展练习，让学生逐步建构起一个完整的知识体系。

例如教学《比的基本性质》一课，练习时笔者设计了这样的两道题：

1.填空：9÷（  ）=（  ）∶35=[35];[（）28]=56∶（  ）=（  ）∶56=4÷7本练习，旨在沟通比与分数、除法之间的关系。

2.计算下列各比的比值，你发现了什么？3∶8=  6∶16=  9∶24=  24∶64=

本练习，复习“求比值”，区别“求比值”与“化简比”不同的同时，让学生发现这些比的比值都相等，为后续学习“比例”相关知识奠定基础。

总之，数学课堂练习不应是单一地做数学，而是要充分关注知识内容本身、学生认知规律、年龄特点、生活背景、知识链接等多个方面，把知识技能、情感态度、实践能力、创新意识以及人生观、价值观的培养融入其中，让练习形式多样、丰富多彩，为孩子们营造一种乐学会学的浓厚氛围，不断提升学生的数学素养。

[参 考 文 献]

[1]李敏.教学练习与作业设计方法[M].北京：中国人事出版社，1996.

[2]郭爱香.练习设计应着眼于学生的可持续学习[J].江西教育，2011（17）.

[3]张圣志.数学课堂练习设计“四性”[J].安徽教育，1997（1）.

（责任编辑：李雪虹）