习题教学中培养学生思维深刻性的课堂探讨
2019-11-18陈土树
陈土树

【内容摘要】课本中的习题是新知识的传授、思维能力的培养、数学思想方法的渗透的主要载体。日常教学中,重视习题教学,能够优化学生的认知结构,从而引导学生乐学、会学,达到减负增效的效果,最终培养学生思维的深刻性。
【关键词】习题教学 一题多解 课堂探讨
科学研究表明:思维品质是思维能力的核心,其中广阔性、灵活性、深刻性、独立性、批判性是它的五大要素。然而一切思维品质的基础是思维的深刻性,思维在深刻性的基础上才引申发展出思维的灵活性和独立性。所谓的思维的深刻性就是指将实际生活中的数学关系进行“提炼”,从而抽象概括出有关的数学问题,然后对数学问题进行分析,采用恰当的数学模型,选择准确的数学方法、运用合适的数学运算,最终求出此模型的解或近似解,以及对解的实践检验和对模型的修正等过程,集中体现为思考的广度、深度、难度三个维度。
一、一题多解——开阔思路,提高思考的广度,在实践中培养思维的深刻性
一题多解是促进学生思维能力发展的有效途径之一,可以培养学生的思维准确性,提高学生的思维灵活性,增强学生思维的深刻性。挖掘多解性就是要挖掘题目中所蕴含知识点的“纵横沟通”,挖掘其中所融汇的多种数学思想或方法,这样有利于发展学生的思考广度,从而培养学生思维的深刻性。在教学中,精心设计具有典型性的范例能极具开发的学生思维。
例1:当x=5-1 ,求代数式x2+5x-6的值。(人教版九上P22 复习题6)
我们日常教学中一般采用一种方法——直接代入。
当 x=5-1时,原式=(5-1)2+5(5-1)-6=35-5 。
如果教师在教学时,就题论题,就失去该题的科学价值,也失去一次培养学生思维深刻性的机会,应与学生共同探索。这一类“求值问题”是简单类型,但是往往这一类题目是我们提高思考的广度,培养思维深刻性的好素材,因为它起点低,入手易。我们可以启发学生研究所求代数式有何特征,进而发现可以因式分解为(x+6)(x-1),从而得到第二种解法:原式=(5+5)(5-2)=35-5。然后引导学生从研究条件入手,并结合所求代数式进行变形:x+1=5 ,原式=(x+1)2+3(x+1)-10=(5)2+35-10=35-5。此时教师适时进行小结,求值问题不仅仅只是直接代入,要注意观察和研究所求代数式与条件之间的联系与变形,能起到“事半功倍”的效果。从多个角度去考虑同一问题,从而培养学生发散思维,提高思维能力,采取不同的方法,让学生自我探究,自我发现,合作交流,在学习中提高学习数学的兴趣,在实践中发展他们的思维能力。
本题通过三种不同的解法,有助于强化不同阶段的知识联系,使不同层次的学生的思维触角伸向不同的方向,让学生优化解题的方法,寻找最优解。看似一道简单的求值题,通过我们的一题多解,不但能起到“以小见大”效果,还能改变传统的教学模式,从而优化学生的思维品质,培养学生的思维深刻性。教材中,还有许多如:一元二次方程的求解,二次函数解析式的求解,平行四边形的证明等等课本习题,教师要善于挖掘,开发有价值的素材,在解决和运用中培养学生思维的深刻性。
二、由浅入深——挖掘内涵,发展思考的深度,在运用中学到深刻的思维
根据初中生的认知规律与思维层次出发,我们平时的教学要循序渐进,螺旋式上升的。通过简单易懂的素材为载体,精心谋划,设计创设思维情境,在不断实践与不断获得成功喜悦之间交替进行,促进学生由浅入深,乐于思考,乐于探索与尝试,从而对某一知识就做到理解深刻。
课本中一些习题,看似平常,但却具有丰富的内涵,我们要善于发现这类习题,引导学生拓展延伸,不能仅仅“做一题练一题”,要通过挖掘其潜在内涵,促使知识深入,提高学生的探索能力,发展学生的思考深度,从而在运用中学到深刻的思维。
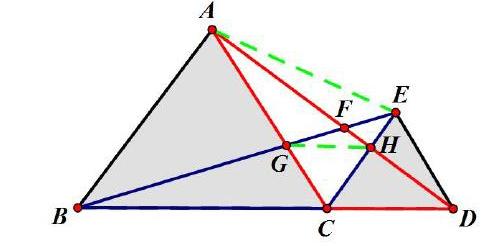
例2:在八上《全等三角形》的教学中,我采用这么一个素材:如图△ABC和△ECD都是等边三角形,点B、C、D共线。第一个问题目标明确,又切合本章所学知识,起点低,学生入手容易,大家都在参与。接着我引导学生能不能得出:BG=AH,为什么?然后在前面的铺垫下,我就全面放手:除此之外,我们还能得出什么结论?上台板书出来。因此在这次的课堂上,学生积极性被调动起来了,思考不断深入,有一条新的结论,大家都是兴高采烈的,都情不自禁的为之鼓掌祝贺。心里又“不服输”,在别人给出结论后,积极思考验证别人的结论是否正确,是否还能推出别的结论。这样打破课堂原有的几何证明题沉闷的气氛,又大大提高了学生思考的积极性,同时对这个图形有了更深刻的记忆,更为深刻的理解,让更多的知识点融合起来,从而于培养学生思维的延伸性,进而学到深刻的思维。
通过这样深入探究与合作交流最后得到了如下①AC∥DE,AB∥CE;②△EBC≌△DAC;③∠AFB=60°;④△GBC≌△HAC;⑤△HCD≌△GCE;⑥GH∥BD;⑦△GHC是等边三角形;⑧ S△ACE= S△ACD= S△BCE等等。虽然这节课结束了,但是学生对这道题的探究还意犹未尽。有一个学生到九年级上学期学《二次函数》知识时,又拿出这道题跟我说:“老师,如果BD长为定值,那么△ABC和△ECD的面积之和有最小值,当且仅當点C为中点时。”可见这道题的深入探究,让学生留下深刻烙印,学到了深刻的思维。
三、一题多变——举一反三,增加思考的难度,在解决中达到深刻的思维
在初中数学中,有很多问题有着深刻的背景,或者蕴含着规律、方法。教学中要善于采用题目条件的弱化与改编,从而提高学生的观察能力,遵循数学从容易到困难,从一般到特殊的学习规律。既培养学生思考问题由浅入深,又极大的提升学生类推能力和梳理归纳的能力,从而提高学生善于观察、比较分析、归纳与探究的意识与能力。这就是思维深刻性培养的高境界。
我们在教学中,采用一题多变,有意识的对条件进行适当弱化或改编,以引导学生进行辨析对比,归类,从而提高了学生从本质上看问题的意识,激起学生强烈的探索精神和求知欲望,更好地培养学生思维的深刻性,提高解题能力。这也同时避免了“茫茫”题海和繁杂资料的烦恼,有效地推行“减负”政策。
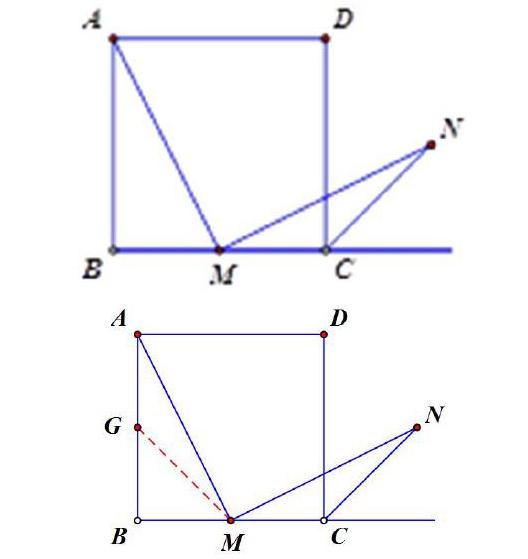
例3:如下图,正方形ABCD中,点M为BC边上的中点,AM⊥MN,正方形外角的平分线CN与MN相交于点N。求证:AM=MN。
分析:本题本质就是三角形全等。如何构造三角形全等呢?大部分同学的想法就是过点N作BC的垂线NH,垂足H,构造出来的三角形NMH与三角形ABM无法证明全等,关键缺少边相等,从而陷入困境。本题在寻求三角形全等时,要牢牢抓住全等的关键——至少有一边相等,而题干中没有边的等量关系,故作辅助线时重点要考量这个要素,即:取AB的中点G,连结MG,通过证明△AGM≌△MCN,本题就迎刃而解了。而这题如果就戛然而止,那么学生就丧失进一步思考的权利,进一步锻炼分析能力的机会,无法使思维深刻化。笔者进行如下四种变式,前两种大背景“正方形”不变,让学生横向迁移;后两种改变“正方形”的大背景,让学生纵向迁移。
变式1:若将原题的条件“点M是BC边上的中点”弱化改为“点M是BC边上的任意一点(M不与B、C两点重合)”,其他条件,如下图所示,此时还有AM=MN的结论吗?
变式2:若将原题的条件“点M是BC边上的中点”进一步改为“点M是BC的延长线上”,其他条件不变,如下图所示,此时还有AM=MN的结论吗?
变式1和变式2通过弱化条件,使得结论更具有一般性。通过原题及改编题的训练,让学生由易到难,渗透了从特殊到一般的数学思想,从而起到培养学生思维的深刻性。
变式3:将原题改为“在正三角形ABC中,点M是BC的延长线上,N是∠ACP的平分线上一点,则当∠AMN= °时,结论AM=MN还成立?请说明理由”
变式4:将原题改为“正n边形ABCD…X中,点M是BC的延长线上,N是∠ACP的平分线上一点,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立”
变式3和变式4,引导学生认真分析,归纳猜想,大胆尝试,发散思维。通过培养与训练,学生能力强了,意识到位了,能在更高、更深的层次上加深对问题的理解,培养学生的思维深刻性。
培养学生思维的深刻性,是数学教育的本质所在。以上三个方面是通过如何习题教学培养学生的深刻思维,当然它们不应是孤立的,而应是相互渗透,并有机融合。课本中的习题是很重要的载体,我们要有目的地去钻研和挖掘,有意识地进行培养和训练。通过对习题挖掘,配上有效的落实途径,适时引导,从而达到培养学生思维深刻性的目的。
【参考文獻】
[1]刘金星.挖掘习题潜能 培养思维能力[J].福建中学数学,2003(10):7-10.
[2]王丽.浅谈数学思维的特性[J].数学学习与研究,2016(2):18.
(作者单位:福建省厦门市第二外国语学校)
