振动-离心复合下土工离心机的 工作模态试验分析
2019-11-18鄂林仲阳杜强王玉军罗昭宇魏晓贞孙爱军
鄂林仲阳,杜强,王玉军,罗昭宇,魏晓贞,孙爱军
(1. 中国工程物理研究院总体工程研究所,四川 绵阳 621999;2. 工程材料与结构冲击振动四川省重点实验室,四川 绵阳 621999)
土工离心机是土力学研究的重要试验设备,利用高速转动产生模拟的重力场,通过增加土体应力的方式,使缩比模型与原型应力应变相等,变形相似,进而模拟波浪、潮汐等环境,解决复杂岩土等问题。其试验结果通常用来验证数值仿真分析方法与计算,是一种重现土工物理过程的有效方法。
在1931 年,美国哥伦比亚大学建造了第一台科学试验土工离心机[1]。1982 年南京水科院的小型离心机和1983 年长江科学院的大型离心机,开启了我国土工离心机的历史[2]。中国工程物理研究院总体工程研究所具有近50 年研制应用离心机的经验,开展了一系列不同规格的土工离心机研制工作,并可以根据用户需要,配置动、静态数据采集系统以及模拟地震波的振动系统等,极大地拓宽了试验范围[3]。随着科技的不断发展,环境模拟从多个单因素简单叠加,向复合环境试验模拟转变,加速度与振动复合是最基本的因素,温度、气压、噪声等可在此基础上复合[4]。离心机的动态特性对其正常运行、设备及试验安全有着重要意义,因此需要对离心机进行模态试验分析,了解其整体及不同运行状态下的动态特性,为后续相关结构设计及优化提供支持,为结构动力学分析及模型修正提供试验数据。
董龙雷[5]结合模态试验结果,将离心振动复合环境实验系统的转臂简化为单自由度系统,建立了振动台的数学模型,分析了振动台与转臂间连接刚度和阻尼对隔振的影响,并设计了具有较好隔振效果的减振器。沈润杰[6]采用有限元法,对离心机的动力学特性进行了分析,得到各阶模态随转速变化的规律,并进行了静止状态下的模态试验,验证了计算结果的可靠性。李峰[7]采用理论计算和试验分析方法,得到了大型土工离心机前几阶模态,并进行了比较,分析表明,连接刚度对计算结果影响较大,在两个方向上激振可以避免漏阶。赵宝忠[8]通过对传感器、实验设备等合理配置,较好地完成了土工离心机模态试验。胡淼[9]采用非线性动力学建模,结合模态试验、仿真、结构动态优化,提出了一套双质体共振式离心机优化设计方案,并进行实例应用。陈怡[10]采用有限元法,进行了卧螺离心机转鼓的刚度强度校核和整机动力学分析,研究了复杂装配结构的建模方法,并分析了双转子结构振动耦合规律,以模态试验数据为依据,进行了参数化模型修正,获得了更为精确的模型。
文中针对某大型土工离心机,运用模态试验方法,分析离心机静止及不同转动加速度下振动台激励时的动态特性。
1 模态试验分析基本理论
模态试验[11]是理论模态分析的逆过程,其基于系统激励和响应的动态测试技术,实际测量输入和输出,经信号处理和参数识别,确定整体的动态特性,建立数学模型。大多情况下,人工进行激励很困难,基于对测点响应的自功率谱和互功率谱进行峰值检索,近似估计共振频率,即为工作模态试验。
连续体结构可离散为一个多自由度系统,其振动方程[12]为:

式中:M 为质量阵;C 为阻尼阵;K 为刚度阵;x 为位移向量;f 为力向量。
考虑线性时不变系统,x 表示为多个线性无关主振型的线性组合:

式中:Φ 为模态矩阵,每列对应一个主振型;ξ是模态坐标。
工程问题中,高阶模态对响应的影响通常很小,可在满足精度要求的前提下,只保留低阶模态。对式(1)进行坐标变换,得到一系列互相独立的方程组:
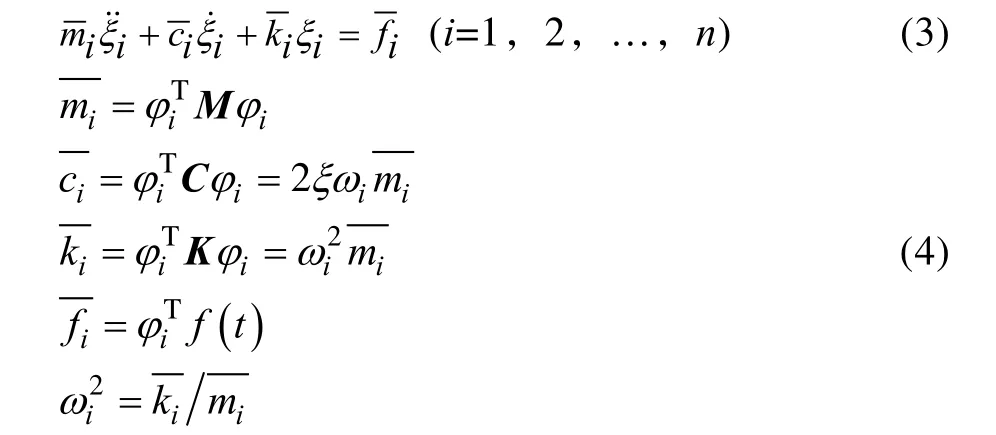
式中:n 为自由度数;ωi是第i 阶固有圆频率。
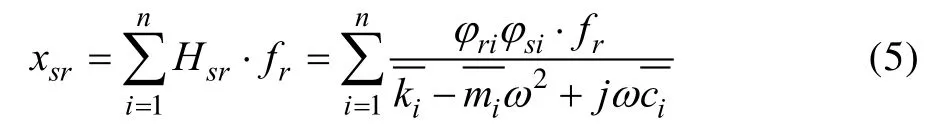
式中:Hsr是测量点与激励点间的传递函数。
对工作模态进行平均处理,Hsr由测量响应的互功率谱和自功率谱求出:

在频域内定义一个类似的无量纲数表示随机函数的相关程度,即相干函数。
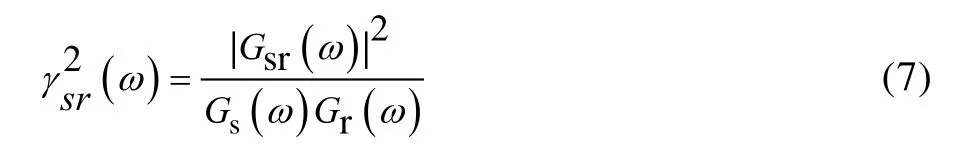
相干函数可用来检查系统是否有随机或非线性干扰。如果其接近于1,表示系统非线性程度很小,噪声干扰也很小,反之干扰比较大,谱密度函数不可信,因为输出不完全由输入引起。
2 常规模态试验
离心机机械系统主要由基座组件、轴承、胀套、转臂、吊篮、配重等部分组成(如图1 所示),整体安装在基础上。常规模态试验中,离心机处于静止非工作状态,含振动台的吊篮自然下垂。试验采用SIMO识别方法,利用力锤产生瞬态激励,可以不产生附加质量,不影响整体的动态特性,以此获得激励点与响应点之间的频响函数。通过模态拟合,得到结构的动态特性参数。

图1 离心机静态试验状态
以离心机主轴中心为坐标原点,以转臂长度方向为x 轴,以垂直地面方向为z 轴,按右手法则建立直角坐标系。在两根转臂上各布置5 个测点,共计10个测点。每个测点均测量z 向加速度响应,测点布局如图2 所示。
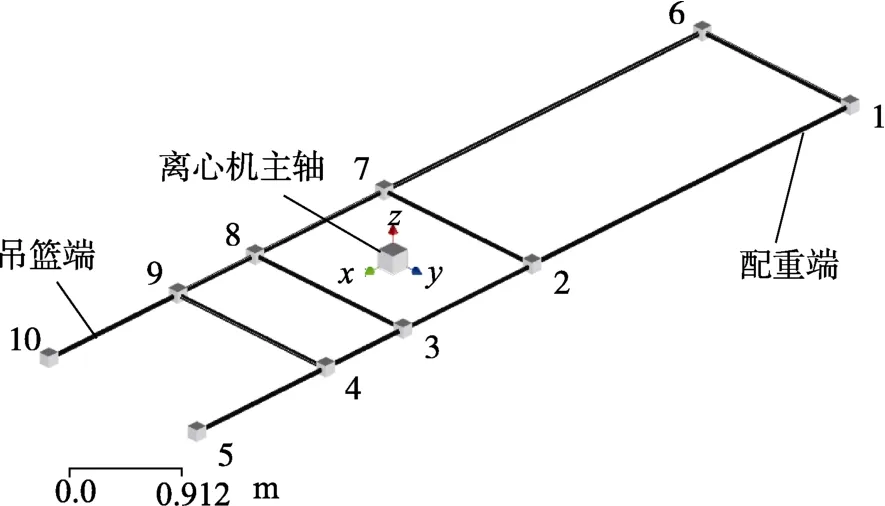
图2 离心机测点布局
通过预试验确定正式试验分析频率为100 Hz,激励点及方向为10z-,进行正式试验。为减少泄漏和噪声误差,分别对激励信号与响应信号加力指数窗和加速度指数窗,如图3 所示。同时取采样帧数为5 帧,即敲击5 次激励点来平均传递函数以消除噪声干扰。各测点频响函数集总平均曲线如图4 所示。
试验结果见表1,模态振型如图5 所示。可以看出,离心机前两阶模态振型表现为绕y 轴和x 轴的偏摆,频率分别为3.23、9.94 Hz,而转臂自身一阶弯曲频率为11.17 Hz。

图3 加窗后10 号点的激励和响应时域信号
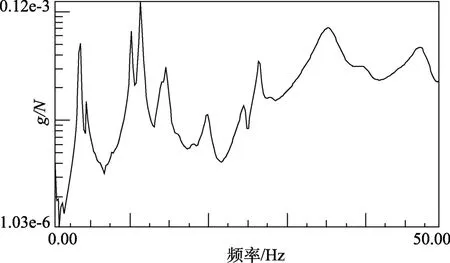
图4 各测点频响集总平均曲线
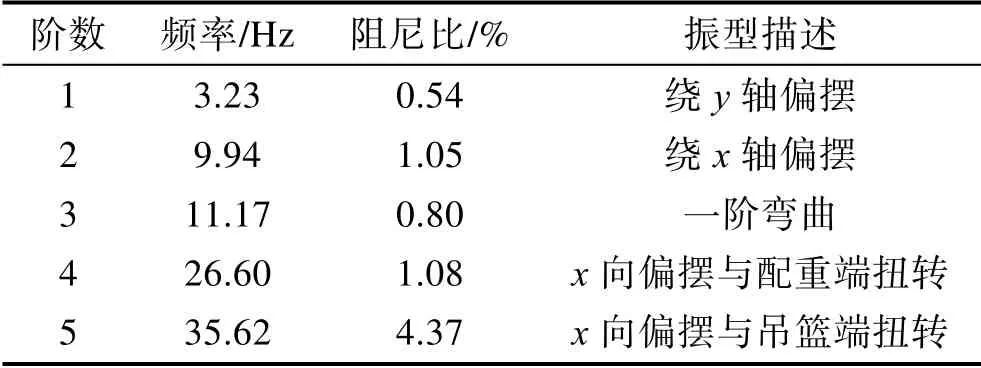
表1 静止时模态试验结果
3 工作模态试验
工作模态试验时,吊篮与转臂基本保持在同一水平面上,不再呈自然下垂状态。加速度传感器测量结构工作状态下的响应,经适当放大变换后,输入计算机,选择2 个以上参考点(节点除外)进行软件互谱分析处理,获得工作模态参数。离心机控制转动加速度分别为10g、30g、50g、80g 和100g,g=9.8 m/s2。振动台施加地震波激励,持续时间为3 s。
振动台上布置了1 个测点(15z+),加速度为10g 和100g 时,15 和10 号测点的加速度时域曲线如图6 所示。

图5 常规模态振型
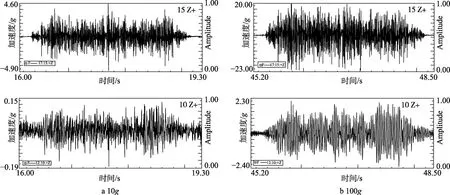
图6 振动台上与转臂上的测点加速度时域曲线
以测点5 和测点10 为参考点,获得结构不同转动加速度下工作模态试验结果,见表2。前二阶工作模态振型(10g 时)如图7 所示。根据有效转动半径计算,不同转速下离心机一阶工作模态频率即为转动频率,模态振型表现为结构的耦合振动;二阶工作模态振型表现为绕y 轴偏摆,频率随着离心机转速的升高而增大,从转动加速度10g 到100g,频率增大了28.41%。
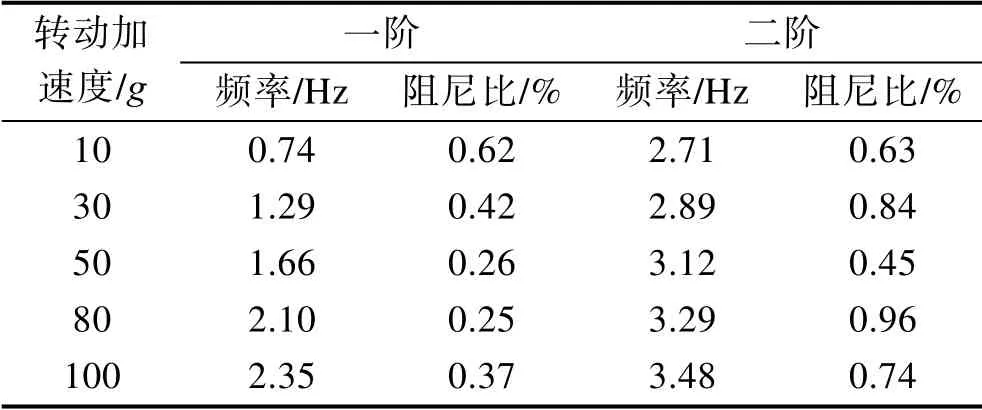
表2 离心机转动时工作模态试验结果

图7 工作模态振型
3 结论
1)某土工离心机静止时前两阶模态表现为绕y轴和绕x 轴偏摆,模态频率分别为3.23、9.94 Hz,自身一阶弯曲频率为11.17 Hz。
2)不同转动加速度下,该离心机一阶工作模态频率为转动频率,模态振型表现为结构整体的耦合振动;二阶工作模态振型表现为绕y 轴偏摆,频率随着转速升高而增大,从10g 到100g,频率增大了28.41%。
3)与静止状态相比,转动时吊篮由竖直状态变成水平状态,绕y 轴偏摆模态的频率。10g 时转臂变长的影响大于离心力刚度硬化效应,频率下降了16.1%;100g 时离心力刚度硬化效应使得频率又上升了7.74%。
4)通过模态试验分析,获得了该土工离心机整体及不同运行状态下的模态参数,试验结果可为有限元模型修正、结构设计及优化提供参考。
