吸能包装模型结构的冲击响应*

谢若泽，钟卫洲，黄西成，张方举

（1. 中国工程物理研究院总体工程研究所，四川 绵阳 621999；2. 工程材料与结构冲击振动四川省重点实验室，四川 绵阳 621999）

各类产品，尤其是武器装备，从研制到使用通常会经历交通运输（空运、车载）和装卸过程，在此过程中可能会遭遇意外事故、经历异常环境，为此需采用包装结构对产品进行有效保护，而包装结构对这些极端情况的耐受性，将很大程度上决定产品的安全性和有效性[1-4]。

包装结构及其内容物经历的异常环境通常包含跌落、火烧、水浸、穿击等，这就要求抗事故包装结构具有承载、耐高温、防火、隔热、抗冲击等功能。国外针对军用抗事故包装结构的研究始于20 世纪60 年代，并于20 世纪70 年代投入生产使用，王宝乾[5]对之进行了分析总结。国内针对抗事故包装结构也进行了相应的研究，如李明海等[6-7]对火灾环境下包装结构的热响应进行了研究，建立了热模型以及相应的计算方法；胡宇鹏等[8]研究了具有内热源的包装结构在不同压力下的传热特性；张鹏等[9]采用ANSYS 软件对空空导弹包装箱在储运过程中的力学环境进行了有限元分析；李娜等[10]探索了包装结构跌落碰撞过程中屈服靶体与非屈服靶体速度关系等效的数学方法。

包装结构的冲击吸能能力是抗事故包装箱研究中的一个重要方面，学者们采用实验、数值模拟等手段进行了各种研究。Michael 等[11]给出了1/4、1/8 比例模型以及全尺寸包装箱的冲击实验结果并进行了有限元分析，鲍平鑫等[12]利用CATIA 建立三维模型，运用ADAMS 对军用爆炸品包装箱铁路运输冲击进行了仿真研究，葛任伟等[13]基于能量转化的思想分析了抗事故包装箱跌落的典型情况，给出了端面跌落和底面跌落时缓冲层厚度的计算公式。

一般来说，对包装箱实物进行全尺寸实验是最可靠的方法，但原型实验不仅实验周期长，而且代价高昂，甚至难以进行，因此在吸能包装结构的设计过程中，采用模型实验和数值模拟两种方法相互配合是很有必要的。分析吸能包装结构的跌落，其本质即为包装结构与地面的碰撞过程，而这种碰撞过程可以采用跌落以外的其他加载方式加以模拟。本文在 ∅ 120 mm 空气炮上对包装结构跌落进行模型实验：对包装结构进行简化和缩比，确定模型试件，将其作为空气炮的弹丸，利用空气炮进行发射，撞击钢靶产生冲击碰撞，利用冲击响应过程模拟吸能包装结构跌落过程。在此基础上，根据模型实验工况开展相应的数值模拟，求解包装结构模型在撞击过程中的应力分布和塑性变形情况，并与模型实验结果进行对比。

1 实验模型

模型实验是一种周期短、成本低的实验方法，能抓住物理本质，为数值模拟提供验证用实验数据，提高数值模拟置信度。模型实验的基本方法是根据相似性原理，模拟结构的几何形状、材料的物理力学特征以及载荷的作用形式，通过室内实验来获得模型的力学规律，为预测原型的变形和破坏提供资料[14-16]。针对抗事故包装箱的跌落冲击问题，周政等[17]进行了详细的量纲分析，建立了相似准则，并通过数值模拟证明了抗事故包装箱原型和模型的应力水平一致性。

模型实验时很难做到完全满足相似条件,实际应用中的模拟多是既使模拟能够进行,又不致引起较大偏差的近似模拟方法。本文的试件根据空气炮口径进行缩比，并保证结构的最小厚度，并未严格按照相似准则进行缩比；基于质量等效考虑，将被保护体采用一定质量的45 钢圆柱替代；同时给予包装缓冲结构一定安全系数，以确保模型试验结果能为原型结构冲击安全评估提供支撑。

缩比后的模型弹如图1 所示，包括外钢壳、云杉木材和被保护体。外钢壳尺寸为 ∅ 120 mm×130 mm，厚度为1 mm，材料为20 钢；被保护体为 ∅ 72 mm×78 mm 圆柱体，材料为45 钢；外钢壳与被保护体之间填充云杉木材，木材的顺纹方向（生长方向）指向被保护体，即被保护体上面和下面木垫层的木材纹路平行于试件轴向，指向被保护体上下表面，被保护体周边的木材纹路则与试件直径方向相同，指向试件圆弧表面。木材与筒体之间、木材与被保护体之间采用环氧树脂胶粘接，钢盖与钢筒之间采用焊接。图2 为模型弹实拍照片。

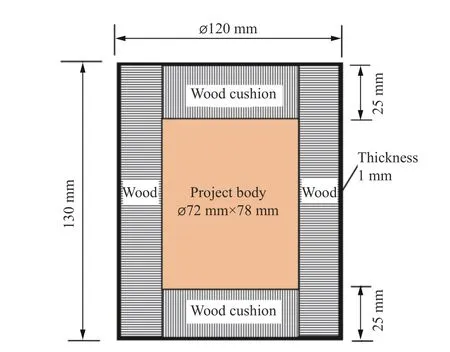
图1 基于包装结构缩比模型的弹丸Fig. 1 Projectile based on scaled model of container

图2 试验弹照片Fig. 2 Photo of experimental projectiles

2 实验设备及设计

模型实验在120 mm 口径的空气炮上进行，测试仪器包括测速仪、高速摄影机、压力传感器等。弹丸速度由红外线测速仪测定，弹丸的撞击过程由高速摄影记录。对于撞击速度低于50 m/s 的正撞实验，在靶架和靶板之间加装压力传感器，以获取撞击过程中弹丸的受力情况；对于撞击速度高于50 m/s 的正撞，因为撞击力太大，超过压力传感器的量程，故取消传感器；斜撞实验极易造成传感器的破坏，因此也未测量其受力情况。

实验设计撞击工况为正撞和30°斜撞两种，斜撞通过调整撞击靶板的法向与炮管轴向的夹角来加以实现。靶板材料为Q235 钢。

图3 为正撞实验靶板安装图。图3(a)为低速正撞实验，压力传感器安装在靶板与靶架之间，靶板为圆形靶板；网格板为高速摄影所用的背景，格线距离为15 mm。图3(b)为高速正撞实验，靶板为方形钢板，靶厚20 mm，通过螺栓直接安装在靶架上。

图4 为30°斜撞实验靶板安装图。靶厚30 mm，通过筋板固定在靶架上，靶板法向从水平线（炮管轴向）向下偏转30°。

图3 正撞实验靶板安装图Fig. 3 Targets in normal impact experiments

图4 30°斜撞实验靶板安装图Fig. 4 Target in oblique impact experiments

3 实验结果

模型实验对正撞和斜撞分别进行了三种速度的实验，其参数如表1 所示。

3.1 正撞

正撞实验的撞击过程如图5 所示,可以看出弹体在飞行和碰靶姿态稳定，能保证弹轴与靶面法线平行一致。图5 中高速摄影的拍摄频率为5 000 s-1，为展示完整过程，图中摘取的图像并非时间上等间隔的。

图6 为实验后的试件形貌。可看到其变形的共同特点是撞击端发生局部屈曲，其中1 号试件的直径在距尾端（即图中的底端）120 mm 的范围内均未发生变化，仅在撞击端略有鼓出，其最大直径为121.8 mm；2 号试件的屈曲程度大于1 号试件，其直径在距尾端116 mm 的范围内未发生变化，在撞击端则鼓出形成皱折，其最大直径为125 mm；3 号试件撞击速度进一步提高，实验后撞击端端盖完全脱落飞出，且后端盖整体向内凹，其直径在距尾端110 mm 的范围内未发生变化，再往撞击端则略微鼓出，在距尾端115 mm的地方则迅速膨出，形成皱折，其最大直径为128 mm。也即，随着撞击速度的提高，局部屈曲的影响范围逐步提高，表现在试件直径的变化范围沿轴向从10 mm 逐步提高到14 mm、20 mm。

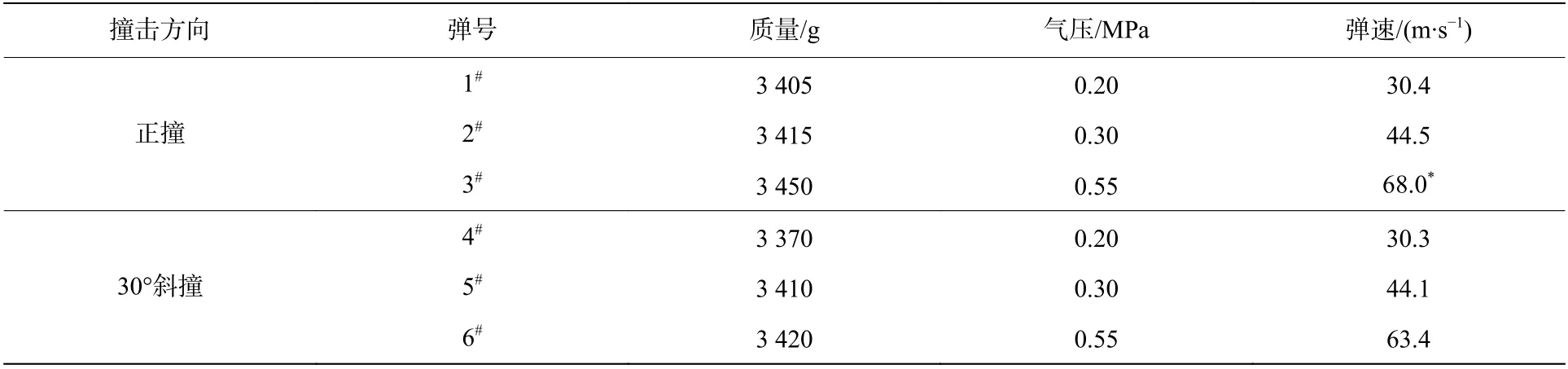
表1 弹丸撞击速度Table 1 Impact velocity of projectile

图5 试件正撞过程高速摄影照片Fig. 5 Process of normal impact

图6 正撞实验后模型弹形貌Fig. 6 Recovery projectiles after normal impact experiment

靶板后压力传感器所测得的载荷时间曲线（2 号弹）如图7 所示，撞击过程持续时间约为0.7 ms，其峰值载荷为576 kN，撞击过程平均载荷为294 kN。

图8 为试验后解剖的弹体内部结构变形与撞击端木垫层形貌图。图中显示，撞击远端木垫层和周边保护层没有明显的变形，而撞击端木垫层已可见贯穿性裂纹，周边部分材料已与主体分离，且中部材料已产生较大压缩，周边形成压塞环。三个试件的压塞环高度分别为2.0、4.2、8.7 mm。而被保护体未产生变形。

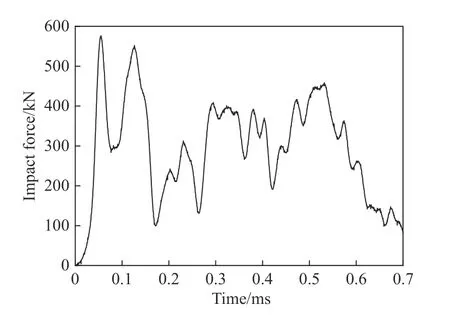
图7 2#弹正撞实验撞击力历程Fig. 7 Impact force history in normal impact experiment(projectile 2#)

图8 正撞实验后弹体内部结构Fig. 8 Internal structure of recovery projectiles of normal impact experiment

3.2 30°斜撞

30°斜撞实验的撞击过程如图9 所示，弹体撞击端上部与靶体发生直接碰撞，反弹回落于靶面下侧。图9 中高速摄影的拍摄频率为5 000 s-1，为展示完整过程，图中摘取的图像并非时间上等间隔的。

图9 试件斜撞过程高速摄影照片Fig. 9 Process of oblique impact

图10 为实验后的试件形貌。可见：撞击端形成撞击斜面，产生压缩变形，且斜面面积和压缩变形量随着撞击速度的增大而增大；斜面的圆弧部分产生皱折，试件总高度略有增加；其他部分变形不明显。撞击速度达到63.4 m/s 时，斜面上出现一个向前突出的月牙面，如图10(d)中箭头处所示，月牙面的平台角度垂直于试件轴线，应为内部被保护体向前冲击形成，经检查，靶面也形成了相应的凹坑；撞击端向前凸出，撞击端盖部分焊接边沿已经崩裂。三种撞击速度下，弹体外径没有发生明显变化的轴向长度分别为99、97 和84 mm，即距离撞击端超过46 mm 的弹体外壳不会产生塑性变形。

图10 斜撞实验后弹体形貌Fig. 10 Recovery projectiles after oblique impact experiment

解剖后观察弹内形貌如图11 所示，可以发现整个撞击端已经发生较大变形，在撞击端木垫层处形成了空腔，木垫层压缩成楔形，楔尖部分已被压塌，且楔体已产生部分崩裂。当撞击速度为30.3 和44.1 m/s 时，被保护体未发生变形。当撞击速度达到63.4 m/s 时，楔尖厚度不到5 mm，不仅楔尖部分已被压塌，而且环形保护层的前端也大部分被压塌。更严重的是，被保护体撞击角也发生了明显变形，形成撞击斜面，前端直径变大，最大直径达到73.6 mm。

图11 斜撞实验后弹体解剖照片（63.4 m/s）Fig. 11 Internal structure of recovery projectiles after oblique impact at the velocity of 63.4 m/s

4 数值模拟

采用ABAQUS/Explicit 有限元分析软件对模型实验情况进行了数值模拟，计算吸能包装结构模型在不同速度、姿态下撞击靶体的动态响应，给出了吸能包装结构模型各部件等效塑性应变分布。计算中靶体模型为 ∅ 1 000 mm×20 mm 钢板，材料为Q235。依据正撞击和30°斜撞击实验条件和相应的结构尺寸建立有限元模型，两种角度撞击有限元模型见图12 和图13。

在有限元模型中木材与外钢壳、被保护体间考虑为接触，将外钢壳作为整体建立模型，忽略结构中的焊接影响。计算中采取的材料参数如表2 所示，其中： ρ 为密度，E为弹性模量，ν 为泊松比，σs为屈服强度，Ep为塑性模量，失效应变为等效塑性应变，通过实验测试和数值计算对比修正获取，主要描述塑性大变形情况对相关材料单元失效行为，45 钢在参考应变率（1 s-1）下屈服强度参数A取为507 MPa、硬化模量B为320 MPa、应变硬化指数n取为0.32、应变率相关系数C为0.064，失效应变参数D1取为0.24、D2取为0.72、D3取为1.62。由于模型中云杉材料顺纹方向垂直于被保护体，实验中木材主要受力方向也垂直于被保护体，因此计算中云杉材料参数采用实验测试得到的顺纹方向压缩曲线[18]。

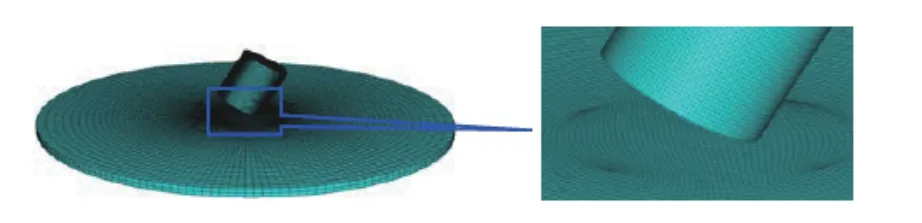
图13 30°斜撞整体模型网格图Fig. 13 FEA meshes for oblique impact

表2 弹靶材料力学性能参数Table 2 Material properties of projectiles and targets

数值模拟中，为了校核数值模拟参数设置的有效性，结合图7 测试撞击力曲线，针对相同工况进行数值模拟给出了相应的冲击力曲线，见图14 所示。可以看出由于撞击过程涉及包装结构材料大变形破坏，导致冲击过程中撞击力曲线振荡略有些差异，但撞击力脉宽和峰值基本一致，可以看出数值模拟结果具有较高可信度。

图15 为对正撞击（68.0 m/s）过程进行数值模拟得到的试件变形与实验结果的对比图，可以看出由于模型试验结构端盖焊接强度较弱，导致端盖脱落，但从总体变形情况两者符合较好，从计算得到的等效塑性应变分布可以看出撞击端在高压力作用下产生环向膨胀，造成撞击端面圆周产生较大应变，在正撞击情况下属于结构的薄弱部位。实验后得到撞击端屈曲后的最大直径为128 mm，试件总高度为125 mm，计算结果撞击端屈曲后的最大直径为132 mm，试件总高度为124 mm，计算与实验结果吻合较好。

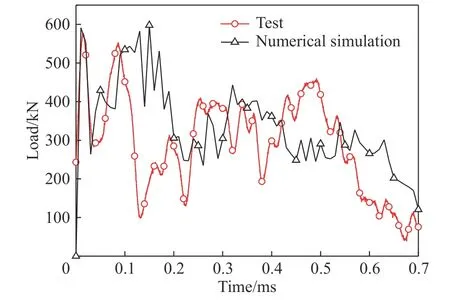
图14 2#弹撞击力试验测试与数值模拟比较Fig. 14 Impact force comparison between experiment and numerical simulation (projectile 2#)

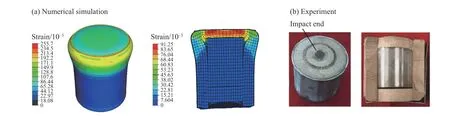
图15 整体变形计算与实验结果对比图（68.0 m/s，正撞）Fig. 15 Comparison of global deformation between simulation and experiment of projectile (68.0 m/s, normal impact)

对斜撞（63.4 m/s）过程进行模拟，所得的试件变形情况与实验对比如图16（图中实验照片里的木垫层已取出示于图17 中），可以看出与实验破坏相对应位置产生的塑性变形较大。撞击端木垫层变形情况的对比见图17，木垫层在斜撞击作用下发生大变形，变成楔形状，实验后所得楔尖厚度不到5 mm，楔尾厚度为24.6 mm，计算结果楔尖厚度为4.9 mm，楔尾最厚处为24.5 mm，计算与实验结果吻合较好。

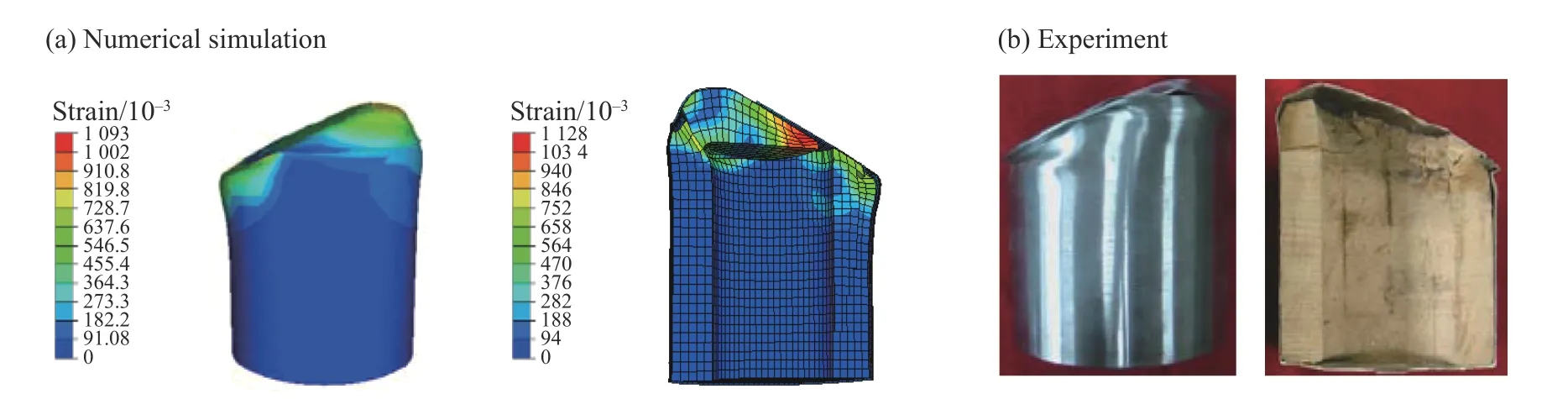
图16 整体变形计算与实验结果对比图（63.4 m/s 斜撞）Fig. 16 Comparison of global deformation between simulation and experiment of projectile (63.4 m/s, oblique impact)

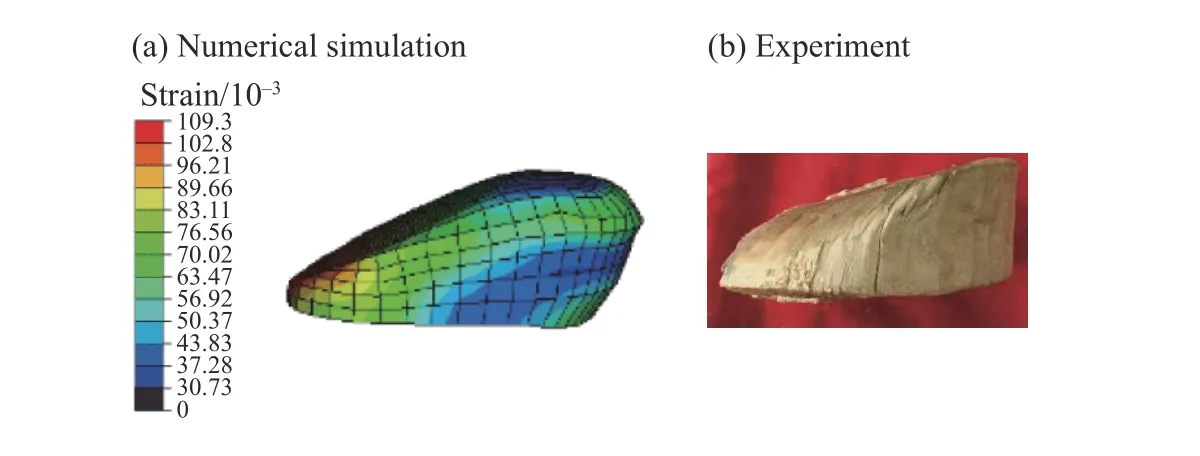
图17 撞击端木垫层变形图（63.4 m/s 斜撞）Fig. 17 Deformation of cushion at the collided end (63.4 m/s, oblique impact)

5 结论与讨论

本文利用空气炮对吸能包装结构的跌落过程进行模拟，进行了缩比模型的正撞和30°斜撞实验，获得了对模型碰撞的直观认识，针对模型实验进行了数值分析，获得了吸能包装结构模型在撞击过程中的应力分布和塑性变形，并将计算情况与实验结果进行了分析，结果表明：

(1) 在撞击中吸能包装结构主要通过缓冲木材的塑性变形及外钢壳屈曲产生的塑性铰吸收能量，其塑性变形主要集中于撞击端，发生塑性变形的最大轴向范围在正撞时为20 mm，斜撞时为46 mm，而远离撞击端未见塑性变形；正撞时，撞击端发生局部屈曲，撞击端木垫层形成压塞环，但被保护体在三种速度下均未发生变形；斜撞时，撞击端形成撞击斜面，撞击端木垫层压缩成楔形，结构变形及破坏程度随撞击速度提高而增大，当撞击速度为30.3 和44.1 m/s 时，被保护体未发生变形，当撞击速度达到63.4 m/s 时，被保护体也形成了明显撞击斜面；

(2) 数值模拟中，木材本构参数采用实验测试获得的顺纹方向压缩应力应变曲线，模拟结果与实验结果吻合较好，说明当木材放置方式为顺纹方向垂直于被保护体面时，木材本构参数采用顺纹方向压缩应力应变曲线具有一定的有效性。

在本文中，木材顺纹方向垂直于被保护体面，而木材具有正交各向异性，将之作为缓冲材料使用时，需针对被保护体所能承受的应力、应变峰值要求，研究不同的木材放置方向对吸能性能的影响，以达到更好的缓冲保护效果。