圆筒装置内爆炸压力载荷特性实验研究*
2019-11-16李芝绒王胜强蒋海燕张玉磊袁建飞
李芝绒,王胜强,蒋海燕,张玉磊,袁建飞
(西安近代化学研究所,陕西 西安 710065)
伴随着精确制导技术的发展,导弹战斗部的毁伤效能成为了战斗部研制和使用部门极为关切和重点关注的问题,特别是反舰型、侵爆型战斗部。了解和掌握战斗部的内爆炸压力载荷特征及分布规律,是检验和评价战斗部毁伤效能的关键。
在密闭环境内,由于壁面结构的约束,爆炸冲击波与壁面结构的耦合效应显著,产生的反射冲击波在壁面间来回反射,形成了比开放环境下更加复杂的压力波流场。目前,由于对内爆炸压力载荷特性的认识尚不完善,在理论上很难建立一个合理的内爆炸载荷解析模型。学者们主要通过数值模拟仿真和模拟实验的方法开展研究:Zyskowski 等[1]开展了小比例模型内爆炸试验和仿真计算,研究内爆炸压力载荷波形特征;黄雪峰等[2]、连赟猛等[3]、樊壮卿等[4]、孔祥韶等[5]开展舱室内爆炸仿真,分析舰船舱室内冲击波流场时空变化和壁面应力变化规律;段雷琳等[6]开展大跨球面钢网壳结构压力载荷的数值模拟计算研究;姚熊亮等[7]开展的舰船舱内爆炸仿真计算,研究冲击波压力载荷波形特征与板架结构的毁伤规律。由于在数值仿真计算中缺乏准确的炸药爆轰产物状态方程,仿真结果只能够定性地表征压力载荷特性,定量结果有一定的误差。模拟内爆炸试验是一种最直观的方法,通过测试手段,获取爆炸压力载荷数据:侯海量等[8]、李伟等[9]开展了舱室内爆炸冲击载荷特性实验研究,分析了爆炸冲击波流场和压力载荷的作用过程以及舱室结构毁伤特性。在内爆炸环境下,特别是钢质立方体模型结构,可能产生大变形或破坏,通常一次使用,试验性价比较高,且由于结构的破坏,常常难以获取完整的测量数据。因此,开展实体模型的内爆炸试验研究较少,可参考的内爆炸载荷特性研究少见文献报道。
本文中,设计一种能够多次使用的圆筒型爆炸装置,开展质量分别为40、80、120 g TNT 装药内爆炸实验,获取壁面、盖板上的压力载荷数据,并结合仿真计算结果,分析研究内爆炸压力载荷的波形特征和分布规律,拟为内爆炸压力载荷特性研究提供参考。
1 实验方法
圆筒爆炸装置如图1(a)所示,主要由圆筒、圆筒两端的法兰盘、前端盖、后端盖、压环、密封圈组成。圆筒长1 670 mm,内径800 mm,壁厚12 mm;前端盖厚度12 mm,后端盖厚度1.5 mm。法兰盘上均布16 个螺栓孔,通过螺杆将圆筒、前后端盖连接,形成了密封装置。装置材料均采用Q235 钢。
在圆筒的经线和端盖的中心线上,分别设置了压力传感器安装孔,圆筒壁面间距200 mm,前端盖间距100 mm,如图1(b)所示。压力传感器选用PCB 公司的113B24、113B22 型压力传感器,量程分别为6.9、34.5 MPa。113B24 型传感器安装于前端盖,113B22 型传感器安装于圆筒壁面,传感器敏感面距圆筒壁面或盖板表面约0.8 mm。传感器安装完成后,在传感器敏感面与安装孔形成的凹槽内涂满油脂,并使油脂表面与圆筒壁面的弧度一致,或与盖板表面平齐。设置油脂的目的是延缓爆炸热向传感器敏感头传递的时间,减小压力传感器测压过程中产生的热冲击信号对压力测量信号的干扰。

图1 圆筒爆炸装置及测点布设位置Fig. 1 Cylinder explosion apparatus and locations of measuring points
实验装药为柱形TNT,质量分别为40、80、120 g,长径比近似1∶1。实验时,TNT 装药放置于圆筒装置几何中心的木质弹架上,药柱几何中心的径向平面与圆筒壁面测点连线在同一平面,由电雷管起爆装药。
2 结果及分析
2.1 实验结果
表1 是质量分别为40、80、120 g TNT 装药在圆筒壁面、端盖的压力载荷峰值测量结果。
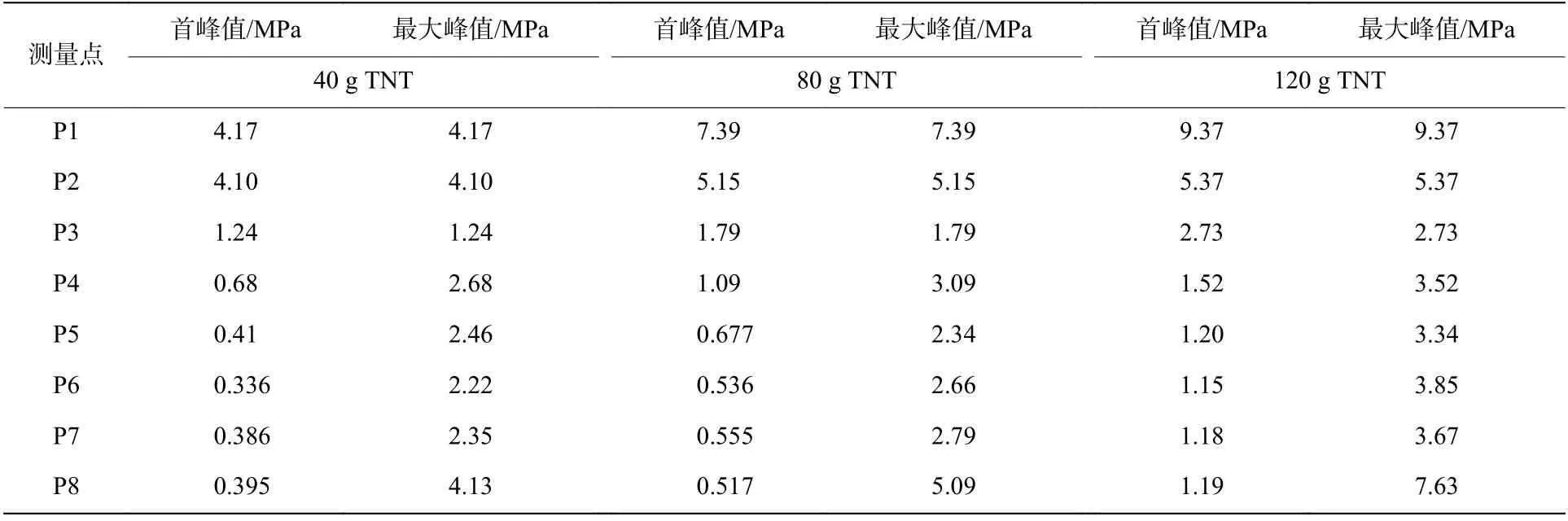
表1 40、80、120 g TNT 装药圆筒壁面、端盖的压力载荷峰值测量结果Table 1 Measurement results of peak pressure of the cylinder wall and cover plate at charge of 40 g, 80 g and 120 g TNT
图2 为120 g TNT 装药圆筒壁面4 个测点获取的冲击波压力载荷曲线。
由图2 和表1 可以看出,在圆筒壁面上,按照爆心距由近到远,压力载荷曲线呈现由显著单波峰向多波峰变化的特点,在爆心近场区域,冲击波首峰值为最大峰值。随着爆心距增大,首峰值逐渐减小,第2 波峰逐渐出现,在角隅区域,第2 波峰甚至超过第1 峰值成为最大峰。从壁面中心到角隅,压力载荷的最大峰值逐渐衰减,然后又增大,呈现了凹形的变化规律。

图2 120 g TNT 装药圆筒壁面测点的压力载荷曲线Fig. 2 Pressure histories of 4 measuring points on cylinder wall at charge of 120 g TNT
图3 为120 g TNT 装药在前端盖板4 个测点获取的冲击波压力载荷曲线。
由图3 和表1 可以看出,圆筒壁面和端盖上的压力载荷曲线特征不完全相同,端盖板上各测点压力载荷曲线呈现多波峰的特点,首峰值较小,第2 峰值最大。各装药4 个测点的首峰值基本相当。除了P8 测点外,各装药P5、P6、P7 测点的最大峰值也基本相当。测点P8 最大峰值比其他3 个测点的最大峰值大,约等于其他3 个测点平均值的1.7~2.1 倍。从端盖中心到角隅,压力载荷最大峰值基本相当,当接近角隅区域时最大峰值突跃增大。

图3 120 g TNT 装药圆筒盖板测点的压力载荷曲线Fig. 3 Pressure histories of four measuring points on cover plate at charge of 120 g TNT
图4 是40、80 g TNT 装药在端盖P7 测点的压力载荷曲线,结合图3(c)的120 g TNT 装药P7 测点的压力载荷曲线,可观察到端盖上压力载荷曲线呈现周期性的压力波动,40 g TNT 前3 个压力波动周期分别为2.48、2.64、2.98 ms,80 g TNT 分别为1.95、2.45、2.58 ms,120 g TNT 分别为1.75、2.30、2.41 ms。各装药的压力波动周期随时间的增长而逐渐变大,后一周期的最大峰值小于前一周期的最大峰值,大约3~4 个周期后,压力波趋于匀化。压力波动周期也随炸药质量的变化而变化,炸药质量越大,压力波动周期越短,质量越小,压力波动周期越长。
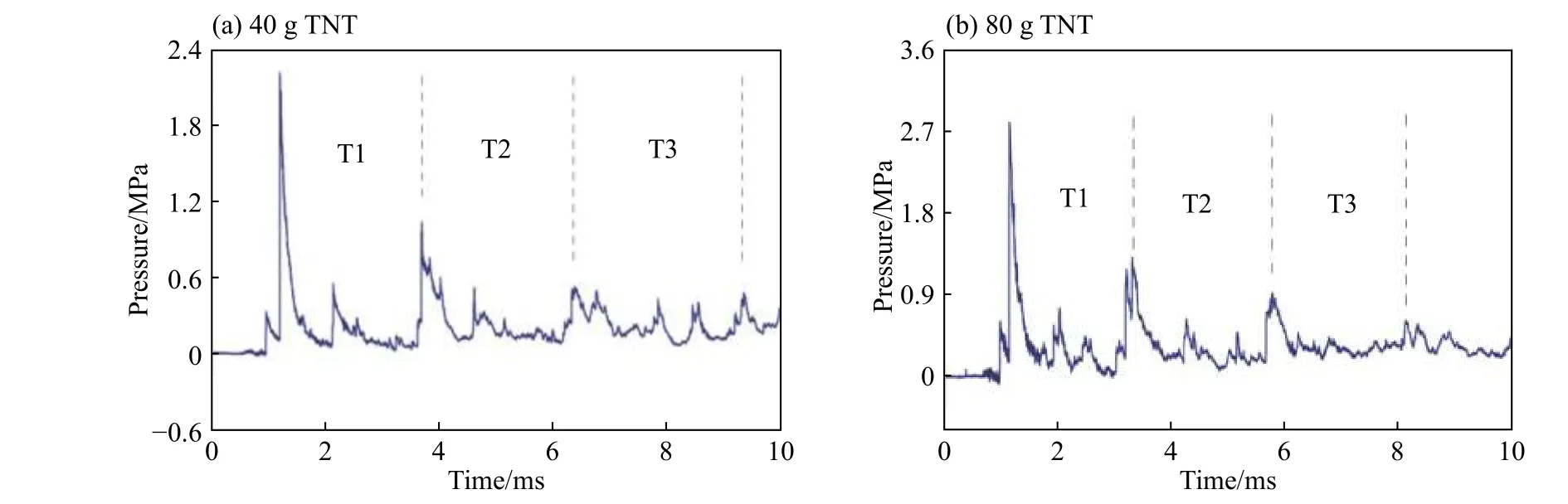
图4 40、80 g TNT 装药在圆筒盖板P7 测点的压力载荷曲线Fig. 4 Pressure histories of P7 measuring points on cover plate at charge of 40 g, 80 g TNT
2.2 圆筒装置内爆炸仿真
为了进一步分析圆筒装置内压力载荷的产生机理,开展了该工况的内爆炸仿真计算。应用有限元分析软件AUTODYN 的Euler 算法,计算炸药装药爆炸冲击波的形成、传播过程。按照试验测点位置,在圆筒壁面、盖板设置观察点,获取观察点冲击波压力载荷随时间的变化曲线。
在仿真计算中,依据圆筒装置几何尺寸及对称性,建立了1/2 模型。考虑到炸药质量小,装置各组成的厚度及强度,圆筒壁面、前端盖采用了实体单元模型;后端盖为薄钢板,采用shell 壳单元模型,圆筒壁与盖板之间采用jion 连接。炸药和空气场采用Euler 网格划分单元。炸药采用JWL 状态方程,空气场采用理想气体状态方程,在装置结构与炸药、空气之间采用流固耦合的计算方法。
图5 是120 g TNT 装药圆筒装置内冲击波压力云图的变化过程。
由图5 可以看出,炸药装药爆炸输出的爆炸冲击波先与圆筒壁面耦合反射(见图5(c)),产生的反射波部分向爆炸中心传播,部分沿圆筒壁面向盖板传播。向爆心传播的壁面反射波在炸点位置区域汇聚(见图5(d)),形成极度压缩的汇聚波,然后膨胀,向周围扩散,形成了两头强、中间弱的梭形二次冲击波向四周传播(见图5(e))。向端盖方向传播的二次冲击波,跟随于爆炸冲击波之后。端盖的中心区域先受到爆炸冲击波的作用(见图5(e)),然后是壁面反射波、二次冲击波、盖板反射冲击波的叠加,形成了复杂压力波与盖板耦合反射,形成的复杂反射波向圆筒中心传播(见图5(f))。在两角角隅区域,先是沿壁面传播的马赫反射波在角隅耦合反射,然后是角隅的反射波、二次冲击波、壁面二次反射波的叠加,在角隅耦合反射,形成复杂反射波向圆筒中心传播。在圆筒壁面、端盖上产生的复杂反射波再次在炸点位置区域再次汇聚(见图5(h)~(i))、压缩,然后膨胀,形成三次冲击波向四周扩散(图5(j)),再次与圆筒壁、端盖耦合反射(见图5(k)~(l))。如此反复多次,冲击波能逐渐转化为气体内能,压力峰值逐渐减小,准静态压力逐渐增大,直至形成压力稳定、均匀的准静态压力场。
由图5 还可以看出,圆筒左右部分的压力云图不对称,主要是由于后端盖为1.5 mm 的薄钢板,在冲击波压力载荷的作用下,板面先从应力最大的两角角隅产生塑性变形,并逐渐向端盖中心扩展。由于板面的外凸,使前、后端盖反射波传播的距离、时间不同步,形成了冲击波流场左右不对称现象。

图5 120 g TNT 装药圆筒装置内爆炸冲击波压力云图Fig. 5 Pressure cloud diagram of cylinder internal explosion blast wave at charge of 120 g TNT
图6 是仿真计算获取的40 g TNT 在盖板P6、P7 测点位置的冲击波压力载荷曲线。P6 测点压力载荷最大峰值为2.15 MPa,P7 测点压力载荷最大峰值为1.87 MPa。与实验对应点的压力载荷对比,测点计算值比实验值小,并且压力波峰的上升前沿比实验曲线缓慢,但是压力波峰出现的时刻与实验基本相同。产生这些差异的主要原因,一是仿真计算中材料模型及参数数值不够准确,二是建模网格密度不高。
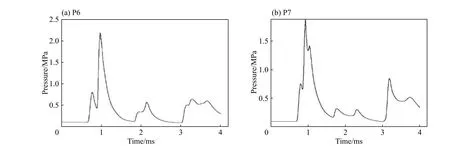
图6 120 g TNT 装药圆筒装置测点P6、P7 的冲击波压力曲线Fig. 6 Pressure histories of P6 and P7 measuring points at charge of 120 g TNT
2.3 圆筒装置压力载荷峰值的表征
2.3.1 圆筒壁面压力载荷峰值表征
从圆筒壁面所受到的压力载荷曲线可以看出,距爆心较近的近场区域,压力载荷曲线呈现单波峰特点。在受到二次冲击波作用之前,爆炸冲击波在壁面传播特性,与地面环境中一定炸高炸药装药爆炸冲击波在地面传播规律类似。因此,圆筒壁面压力载荷的首峰值,可依据爆炸冲击波在地面传播模型计算[10]。当入射角小于39.14°时,冲击波产生规则反射。在规则反射区内,当冲击波产生正反射时,冲击波压力首峰值角度为:

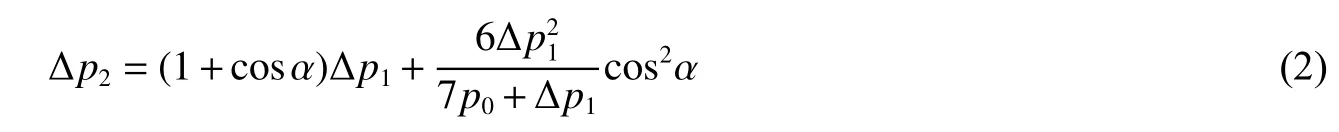
当入射角大于39.14°时,在地面环境,冲击波产生马赫反射现象。马赫反射区冲击波参数的计算相对复杂,参考易仰贤[11]的马赫反射压近似计算公式(3)~(4),得到:

式中:α为冲击波入射角;r*、α*分别为马赫反射起点处的爆心距、入射角;r为测点处的爆心距。
将模型计算结果与试验测量结果比对,对于规则反射区,正反射点冲击波压力载荷首峰值的偏差小于5%,斜反射点压力载荷首峰值的偏差小于14%;对于马赫反射区,除了40 g TNT 偏差较大外,其他测点压力载荷首峰值的偏差小于13%。
2.3.2 圆筒端盖压力载荷峰值表征
从圆筒端盖所受到的压力载荷曲线和仿真计算压力云图可以看出,端盖上先受到了爆炸冲击波的作用,与圆筒壁面类似。在受到其他冲击波作用之前,爆炸冲击波的传播特性,与地面环境中一定炸高炸药装药爆炸冲击波在地面的传播规律类似。由于端盖各测点产生规则反射,因此,各测点压力载荷的首峰值可依据入射角用式(1)或式(2)计算。比对计算结果与试验测量结果,测点P5 首峰的偏差小于10%;斜反射测点P6、P7、P8 首峰的偏差的小于16%。
由表1 的实验结果可知,40、80、120 g TNT 装药在端盖中心区域的最大峰值等于各自首峰值的6.23、4.48、3.07 倍,在角隅区域的最大峰值等于各首峰值的10.46、9.85、6.52 倍。由图5 可以看出,由于压力载荷的最大压力峰值是多波耦合叠加结果,形成机理复杂,目前还无法建立一个合理的解析模型。因此,依据爆炸相似定律,按照实验工况和实验炸药装药质量,可以认为:在长径比为2∶1 的圆筒端盖上,在冲击波入射角小于13.5°的中心区域,对比距离为1.74~2.50 时,压力载荷的最大峰值大于首峰值的3 倍;在冲击波入射角为19.7°~25.6°的角隅区域,对比距离为1.80~2.70 时,压力载荷的最大峰值大于首峰值的6 倍。
2.4 内爆炸冲击波压力载荷的衰减特性
从获取的圆筒装置所受到的压力载荷曲线可以看出,冲击波经过3~4 个周期性波动后逐渐匀化,在圆筒内形成了稳定、均匀的准静态压力,如图7 所示。冲击波最大峰值的周期性衰减特性,大致符合Anderson 等[12]得到的反射冲击波峰值为前一个反射冲击波峰值的一半的规律。主要差异表现为,在第2 周期以后,后一个冲击波最大峰值比前一个冲击波最大峰值的一半略大。主要原因为:一方面是圆筒内的准静态压力提高了圆筒的整体压力,增大了压力载荷峰值的绝对值;另一方面可能是由测量系统的测量误差引起。如采用的PCB 压力传感器低频响应特性(-5%)为0.005 Hz,用于测量准静态压力时会产生测量误差;如爆炸热持续作用于压力传感器的敏感面上,传感器输出的热响应信号叠加到压力测量信号中,造成了准静态压力的测量误差。
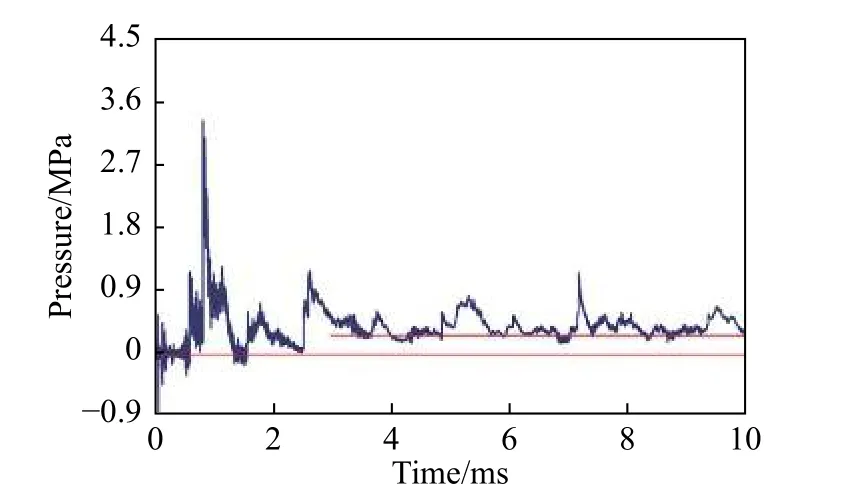
图7 圆筒结构冲击波压力载荷曲线Fig. 7 Pressure histories of cylinder
3 结 论
通过在圆筒型装置内的爆炸试验,分析了长径比2∶1 圆筒壁面、端盖上压力载荷特征,结论如下。
(1)圆筒壁面的压力载荷按照爆心距由近到远,从显著的单波峰向多峰值变化。在近场区域压力载荷衰减特性与一定炸高自由地面冲击波传播特性类似,压力载荷的首峰值可按照规则反射区和马赫反射区的压力峰值计算公式得到。
(2)端盖上压力载荷呈多波峰特点。在中心区域,对比距离为1.74~2.50 时,压力载荷的最大峰值大于首峰值的3 倍;在角隅区域,对比距离为1.80~2.70 时,压力载荷的最大峰值大于首峰值的6 倍。
(3)在圆筒壁面和盖板上,从几何中心到角隅区域,压力载荷峰值呈凹型分布特征;在盖板上,从几何中心到角隅区域,压力载荷最大峰值基本相当,当接近角隅区域时最大峰值突跃增大。
(4)圆筒内冲击波经过3~4 个周期性波动后,冲击波压力逐渐匀化,形成了稳定、均匀的准静态压力。
虽然用试验和数值模拟的方法,验证了TNT 装药在该工况和有限质量范围内压力载荷的特征和分布规律。但对于其他比例模型的圆筒装置,本文的结论是否适合,还有待于进一步验证。由于内爆炸冲击波的反射及叠加效应复杂,今后还需要进一步研究。
